基于偏离度优化的高速列车轴箱轴承温度预测方法*

孟建军 潘彦龙 陈晓强 李德仓 胥如迅

(①兰州交通大学机电技术研究所,甘肃 兰州730070；②甘肃省物流及运输装备信息化工程技术研究中心,甘肃 兰州 730070；③兰州交通大学机电工程学院,甘肃 兰州 730070；)

转向架上轴箱、齿轮箱、电机等重要位置都分布有轴承，在确保列车运行安全方面，轴承是不可或缺的[1]。

列车运行中轴承异常温升是危及铁路运输安全的严重故障，轻则造成紧急停车引起经济损失，重则可能引发列车脱轨危及旅客生命安全[2]。温度可以直接反应轴承的工作状态，温度的异常是轴承发生故障的重要信号。现有车载轴温监测系统可以对轴温进行实时监测，通过设定的阈值来对轴温进行预警。但是一旦发生报警，必须立即进行处理，留给相关人员的处理时间少。因此，通过对高速列车的轴温进行预测追踪，提前掌握下一时段轴温的变化趋势，为处理轴温异常预留足够时间，对高速列车预警及调整行车策略有重要的工程价值[3]。

针对温度的预测研究，Qiu Rujian等采用长短期记忆网络对河流日水温进行预测[4]。张恒志等根据车载系统收集的走行部数据是多维时间序列的特点，提出一种基于稀疏注意力机制的城轨车辆轴温预测模型[5]。宋佳音采用加权混合法和卡尔曼融合算法对ARIMA模型和PSO-SVM模型进行了融合分析[6]。张继冬等建立了基于服役工况参数的SVM轴承温度预测模型[7]。梁涛等基于灰色关联度理论提出变权组合方法对齿轮箱温度进行预测[8]。Hrachya Astsatryan等通过气象台站收集的观测数据，用基于机器学习的方法对亚美尼亚地区气温进行预测[9]。尹艳松等采用非线性状态估计(NSET)的方法对轴承温度进行预测研究[10]。叶钰等提出无线通信的正交试验方法来分析耦合因素对高速电主轴的热误差作用[11]。

目前对轴温进行提前追踪预测的研究较少，在列车上轴温测点较多，各种轴承之间的工况差异较大，并且热轴故障是铁路运营单位极力避免的重大故障，发生次数较少。列车轴温数据采集频率低且引起轴温升高的因素多样，在仅知道温度的前提下为灰色系统。因灰色理论具有建模样本少，精度较高的优点，利用灰色理论对轴温进行预测可以有效解决数据量少的问题。

1 基于灰色理论的列车轴温预测模型参数优选

在用灰色理论建模对轴温进行预测时，除了选择轴温序列外，对于模型的建模数、预测的步长这3个参数进行阐述说明。并通过分析统计结果，对建模参数及迭代数进行选择。

1.1 建模参数说明

1.1.1预测数

预测数即预测步长，使用前mmin分钟的历史轴温数据预测后续nmin分钟的轴温数据。建立模型前，需要对轴温预测步长进行选择。预测步长过大模型预测精度将降低，预测步长过小则会造成不能满足实际需要。

1.1.2建模数

本文引用文献[3]建模数的概念，用建模数代指构建模型所需要的数据点个数。在用灰色理论进行轴温预测时，选择不同的建模数会影响模型的精度。建模数过少则不能反映轴温变化的整体规律，造成模型的精度下降。建模数过多，不仅会造成模型的计算效率降低，由于包括的陈旧信息过多，造成信息冗余，不能将轴温最新的发展趋势展示出来。因而需要根据实际需要选择合理的建模数。

1.1.3预处理参数

本文研究车载轴温监测系统所用的温度传感器为pt100，采样频率为1/60 Hz，采样精度为1 ℃。轴温数据每分钟传输一次且为整数。由于采集到的原始轴温监测数据质量较差，存在缺失、重复、阶跃等问题，因而需要对传感器采集到的轴温数据进行预处理。对轴温监测数据中的跳变点进行删除处理，对温度缺失值插值处理，对温度信号平滑处理以提高模型的精度。因曲线拟合方法会由于核函数选择的不同，导致轴温的变化情况呈现核函数的温升规律，不能正确反映原始轴温的温升规律。选用滑动平均处理的方式则不会对原始数据变化规律造成影响。

设选取的原始轴温数据为X=[x1,x2,…,xn]，则经过滑动处理后的数据为X(0)为：

(1)

滑动处理的数据可以重复进行相同的处理，重复处理数据的次数为迭代次数。适当的迭代次数可以提高数据的平滑度进而保证模型的精度，但是迭代次数过多，数据会过于平滑而失真，使得不能正确反映温升规律，造成模型的准确度下降。

1.2 建模参数选择

通过查阅相关资料，预测时间越长，则模型的预测精度会得不到保证。选择5 min的短时预测，便可满足车辆实际运营时的轴温预测需求[12]。因而本文选择预测数为5。

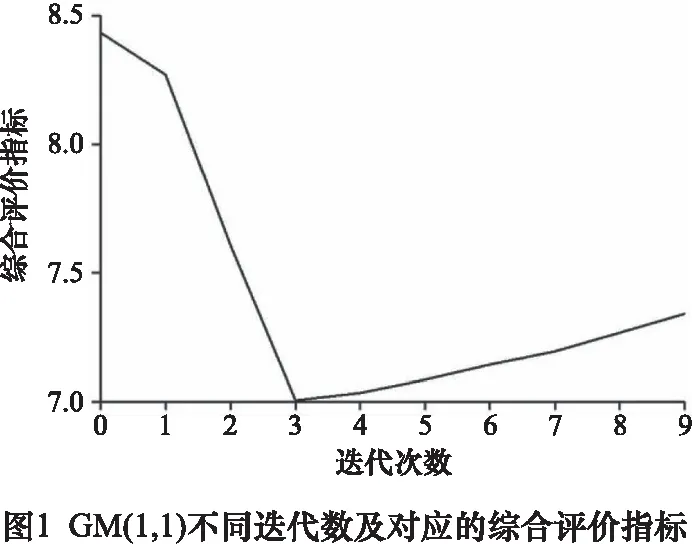
为选择合适的迭代数及建模数，对某型高速列车的历史轴温数据进行预测，将最大绝对误差与平均绝对误差的和作为综合评价指标。对不同迭代数对应的综合评价指标进行统计，结果如图1所示。

由图1可以看出迭代数为3时，综合评价指标最小，模型的性能更佳。在选定迭代数为3的情况下，对不同建模数进行综合评价指标统计，如图2所示，得出建模数一般选6～8为宜。

2 基于灰色二次回归的轴温预测模型

2.1 基于GM(1,1)的轴温预测模型

设序列X(0)=[x(0)(1),x(0)(2),…,x(0)(n)]，其中x(0)(k)≥0,k=1,2,...，n;X(1)序列为X(0)序列的1-AGO序列[13]：

X(1)=[x(1)(1),x(1)(2),…,x(1)(n)]

(2)

其中：

(3)

Z(1)=[z(1)(2),z(1)(3),…,z(1)(n)]

(4)

(5)

则GM(1,1)模型为[14]：

x(0)(k)+az(1)(k)=b

(6)

其中a为发展系数，b为灰作用量。

(7)

其中：

(8)

GM(1,1)模型的解：

(9)

最终GM(1,1)模型求得的预测值为：

(10)

2.2 基于灰色二次回归的轴温预测模型

灰色二次回归模型是将二次多项式与GM(1,1)模型融合，使用最小二乘法求解模型的参数，从而确定模型。

GM(1,1)模型的解可记为：

(11)

基于灰色二次回归的时序预测模型则使用指数方程Y=aebx和二次多项式方程Y=aX2+bX来拟合x(1)(i)，记作：

(12)

其中参数v由GM(1,1)模型计算得出a后，使得v=-a，C1、C2、C3和C4则通过使用最小二乘法得出，求解方法为：

(13)

(14)

GM(1,1)的解为指数形式的，因此GM(1,1)实质是指数的拟合模型。在使用GM(1,1)模型对接近指数上升的单调变化的曲线进行拟合时效果较好，但是对凹凸变化的曲线拟合的误差较大。

2.3 轴温波动序列测试结果

以一段高速列车实际轴温波动数据为例，采用灰色二次回归预测模型与GM(1,1)模型进行预测，如图3所示。结果显示，灰色二次回归模型跟实际轴温的拟合较好。由于GM(1,1)具有指数增长的性质，因而在轴温预测时会出现预测值比实际值偏高的现象，灰色二次多形式是对GM(1,1)模型的改进，可以在一定程度上规避这一现象。

同理，用两种模型对轴温曲线进行拟合预测时，GM(1,1)模型由于其特有的属性，其对单调变化的曲线有更好的拟合，灰色二次回归模型对凹凸变化的轴温曲线有较好的拟合能力。

3 基于偏离度的灰色二次回归与GM(1,1)组合预测模型

3.1 模型构建

选择相对邻近的历史轴温数据，建立预测模型对轴温进行短时预测。当轴温达到最小建模的数据量，利用模型预测未来n分钟的温度，每n分钟对输入模型的轴温数据进行更新。并重新根据更新的数据建立模型，预测下一个n分钟的轴温。当用第i个预测模型时，前一个预测模型与实测值的偏差变成已知。根据第(i-1)个GM(1,1)模型与灰色二次回归预测的偏差确定权值w1、w2，以此来修正误差。在(t-n)时GM(1,1)与灰色二次回归模型预测后n分钟输出轴温和实测轴温为：

(15)

式中:PGM(1,1)为GM(1,1)预测输出序列。

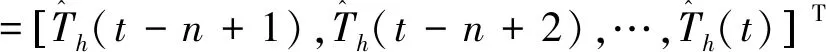
(16)

式中:P灰为灰色二次回归预测输出序列。

T=[T(t-n+1),T(t-n+2),…，T(t)]T(17)

式中:T为实际温度向量。

两种模型预测向量与实测向量之间的距离d为：

(18)

根据模型预测值距离实测值的偏差大小来重新分配两个模型的权重。以两种模型的距离来计算权重，当与实测值之间的偏差愈小占比愈大。

(19)

式中:wGM(1,1)为GM(1,1)模型所占权重，d灰为灰色二次回归预测值与实测值之间的距离，∑d为两种函数预测值与真值距离之和。

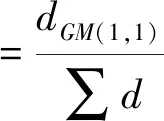
(20)

式中:w灰为灰色回归权重，dGM(1,1)为GM(1,1)模型预测值跟实际温度的距离。

在t时刻将n个轴温监测数据更新后，模型的输入发生变化，根据最新的输入向量输出预测向量，并根据(t-n)时刻的预测偏差对模型进行加权重构即：

(21)

采用偏离度组合的预测模型对轴温进行预测的步骤如图4所示。

为提高模型的精度，将建模窗口内的数据及时进行更新，做到吐故纳新，能够将最新的轴温信息运用到模型中，从而在建模数没有变化的情况下，提高模型的预测精度，保证模型的可靠性。将模型第一次求得的预测值与之后求出的预测值拼接起来，便可得到完整的预测轴温序列。

3.2 模型评价指标

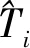
表1 预测误差评价指标

3.3 实例验证

以某型高速列车履历服役轴温监测数据为例，来验证本文提出的模型的准确性与可靠性。以高速列车轴箱轴承温度为例，基于轴箱轴承数天履历数据，运用偏离度优化的预测模型对轴温进行预测，并在每n分钟后更新模型输入数据，根据前一时刻单一模型预测的误差对模型重新进行加权校正，以此优化该组合模型。图5为高速列车温度传感器安装位置示意图。

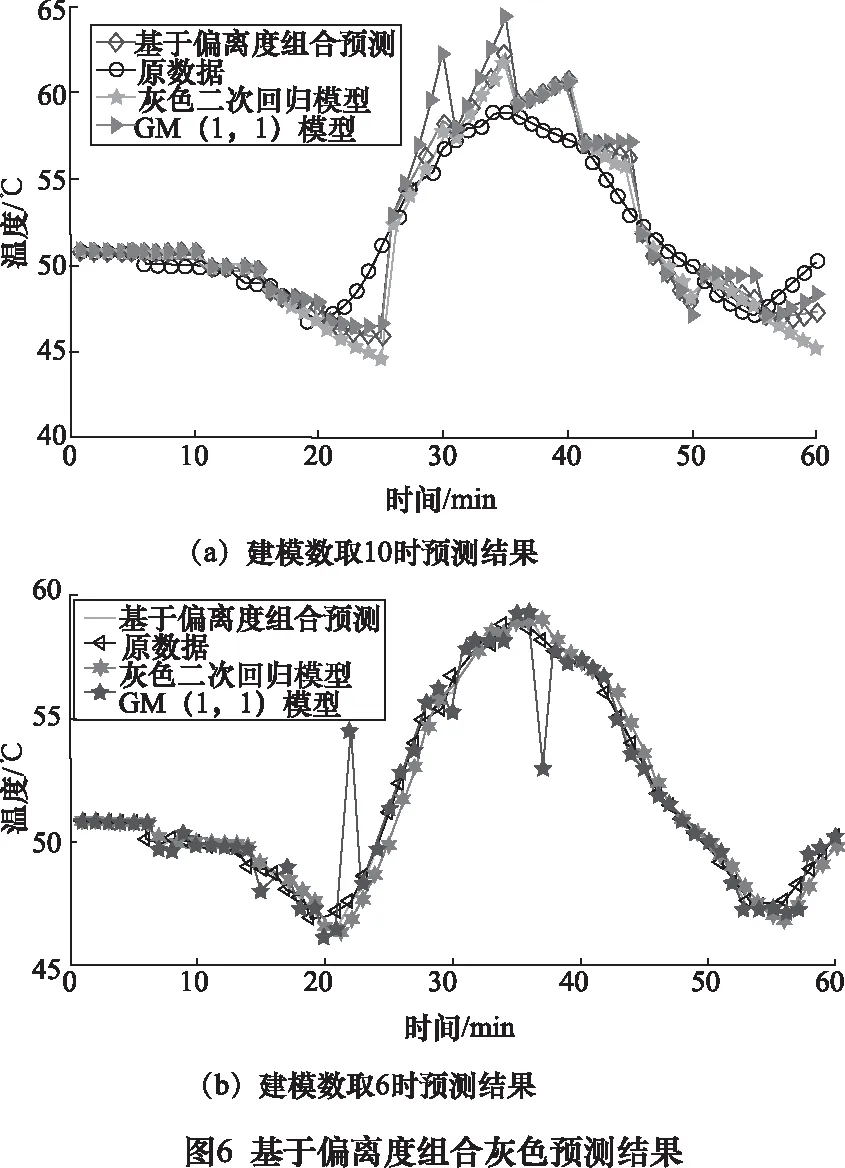
采用灰色二次回归模型、GM(1,1)模型、基于偏离度优化的组合模型对某型高速列车的历史轴温进行短时预测，建模数分别取10、6时预测结果如图6所示，预测误差统计结果如表2所示。

对预测结果进行分析，可以看出建模数一般取6左右时有较好的拟合效果，在对轴温进行短时预测时，基于偏离度的组合模型最大绝对误差为0.98，平均绝对误差为0.19。显然，基于偏离度优化的模型较单一预测误差明显减少，预测精度有较大的改善，表明模型的优化作用有效。

表2 基于偏离度优化的组合模型温度预测误差

4 结语

(1)基于GM(1,1)对单调变化的曲线拟合度较高、灰色二次回归模型对凹凸变化的轴温曲线拟合较好的情况，将两个模型组合起来预测轴温。选用某线路上实测轴温数据对模型进行验证，结果显示基于偏离度优化的组合模型适应性更高，预测结果更平稳，预测精度较单一模型得到有效改善。

(2) 通过对建模数及迭代数的合理选择，对原始轴温数据进行预处理，保证满足建模的需求。此外，为及时的感知轴温变化情况，对建模窗口内的数据不断更新，保证数据的实时性，将最新的轴温变化情况反映出来。根据两个单一模型上一时段预测的偏差，对单一模型的权重系数及时调整，进而重新组合预测。对异常温升测点在未来短时间内的温度预测，争取到更多的处理时间，为行车策略调整提供依据。

(3)组合预测的方式可以博采众长，整合单一模型的优点，提高模型的适用性。本文将两个单一模型的权值系数进行偏离度优化调整，即不是均值加权的。这种方式可以避免均值加权时，组合模型不能对表现较好模型的优点充分发挥出来的情况。