数控加工工艺参数的多目标优化与决策算法研究*

刘海亮 贾翠玲 王东辉

(内蒙古工业大学工程训练教学部，内蒙古 呼和浩特010062)

数控加工技术是在传统制造技术基础上集成了自动控制技术、计算机技术和网络通信技术而成的产物。与传统机械制造比，具有自动化程度高、生产效率高、质量高等诸多优势[1]。工艺参数作为数控加工的可控参数，参数数值的设置极大地影响数控加工质量，对参数进行优化可以提高生产效率和生产质量，同时降低生产成本，因此研究参数优化问题具有重要的实际意义。

依据优化目标的不同，数控加工技术的优化可以分为能耗优化、生产效率/成本优化、刀具磨损/寿命优化、生产质量优化等。文献[2]面向数控机床能耗进行优化，根据机床闲置时间制定机床待命、系统待命和关机3种控制方案，实现了数控机床的智能化低能耗控制。文献[3]使用响应面法对金属加工过程中的能耗和刀具使用寿命进行优化，得到了刀尖半径对目标参数的影响规律。文献[4]为了降低机床热误差对数控机床加工精度的影响，使用布谷鸟算法优化灰色GM(1,N)模型的系数，提高了灰色模型预测精度，为热误差补偿提供了依据。文献[5]使用灰色关联分析、主成分分析、响应面等方法对工件表面粗糙度和能耗进行优化，得到了优化的进给速度、切削深度、切削速度等参数。当前关于数控加工工艺优化面临2个难题：一是优化目标经验公式精度略低，且不具有个体差异的适应性，难以满足高要求的优化问题；二是优化模型的求解方法需进一步研究，力求得到最优参数，而不是次优参数。

本文针对汽油机活塞的数控车削加工过程，以提高加工质量和生产效率为目标建立了多目标优化模型。使用非支配排序差分进行算法进行模型求解，并提出了基于加权相对距离的决策算法。经过优化和决策，实现了提高生产质量和生产效率的目的。

1 问题描述与建模

1.1 问题描述

本文以某汽油机活塞的数控车削加工过程为研究背景，对数控加工的产品质量和加工速率进行优化。汽油机活塞材料为铝硅合金，活塞尺寸为φ81.5 mm×50 mm，经车削和铣削后的最终产品如图1所示，本文只研究车削过程的优化问题。加工前毛坯为圆柱体，尺寸为φ85 mm×55 mm。

实验用车床为FeelErftc-350型车床，如图2所示。刀具为PCD活塞外圆专用刀具，刀具前角为5°，后角为11°，刀尖圆弧直径为1.0 mm。

1.2 问题建模

对于多目标优化问题，其数学模型包括建立目标模型、设计优化参数、设置约束条件等3个方面。

(1)建立目标模型。对1.1节设置的研究背景，本文以零件表面粗糙度Ra、材料去除速率Q为优化目标。零件的表面粗糙度越小则零件质量越好，因此零件表面粗糙度是一个最小化目标；材料去除速率越大则车削加工速率越大，因此材料去除速率是一个最大化目标。综合以上分析，得到多目标优化函数为：

obj.f=(minRa)∩(maxQ)

(1)

零件表面粗糙度有经验公式可以使用，为：

(2)

式中：af为每转进给量，r为刀具半径。

材料去除速率是衡量数控车床加工的重要指标，是指单位时间内切除掉的材料体积，其完全由切削速度、背吃刀量和每转进给量决定，即：

Q=ae·ap·af

(3)

式中：ae为切削速度，ap为背吃刀量。

在此需要强调的是，材料去除率计算公式为精确计算公式，可以直接应用。但是零件表面粗糙率为经验计算公式，计算精度有限。

(2)设计优化参数。选择工艺参数切削速度ae、背吃刀量ap、每转进给量af为优化参数，则3个参数形成的优化向量表示为x=(ae,ap,af)。

(3)设置约束条件。本次优化问题的约束条件包括优化参数取值范围约束、零件质量参数取值范围约束、数控车床加工能力约束等，即：

(4)

式中：Fmax为最大切削力，Wmax为最大功率。

2 工艺参数-目标参数映射策略

在1.2节中提到，材料去除速率为精确计算公式，可以直接使用；但是零件表面粗糙度是经验计算公式，其计算精度有限，且对每次加工、不同设备不具有自适应性和个体差异性。为了更加精确地对参数进行优化，本文使用神经网络对工艺参数与目标参数间的关系进行映射。

2.1 学习效率自适应神经网络设计

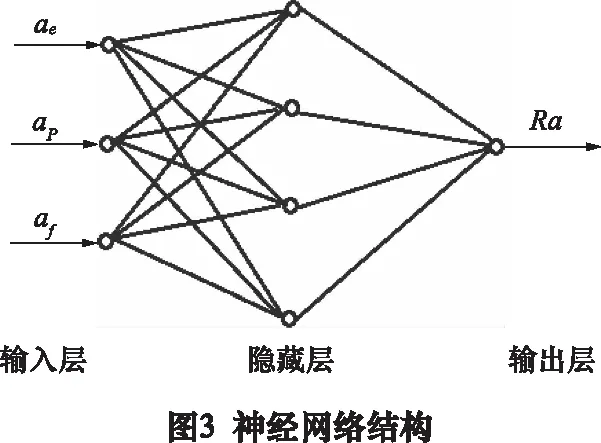
简单地讲，BP神经网络地构建需要3个步骤，分别为数据预处理、数据前向传播、基于误差反向传播的参数修正。

(1)数据预处理。输入输出数据的量纲相差较大时会降低训练速度，因此需要对输入输出数据进行归一化处理，即

(5)

式中：xmin为参数最小值，xmax为参数最大值，x为参数原始数据，x′为参数归一化后数据。

(2)数据的正向传播。数据正向传播即为神经网络的输出过程[7]。

(6)

式中：O为神经网络输出；xi(i=1,2,3)为神经网络输入，x1表示ae，x2表示ap，x3表示af；wij为输入神经元i与隐藏神经元j的传递权值；θj为隐藏神经元j的阈值；vj为隐藏神经元j向输出神经元的权值，r为输出神经元阈值。f1为隐藏神经元激活函数，使用Tansig函数；f1为输出神经元激活函数，使用Tansig函数。

(3)参数训练。首先计算拟合误差，为：

(7)

式中：E为训练误差，U为数据长度，yi为样本输出，Oi为拟合输出。

以传递权值wij为例，参数的训练方法为：

(8)

式中：Δwij(t)为迭代t次时的参数修正值，η为学习效率。传统神经网络一般使用固定的学习效率，但是学习效率过小容易陷入局部最优，过大则收敛速度过慢，因此本文设置自适应学习效率为：

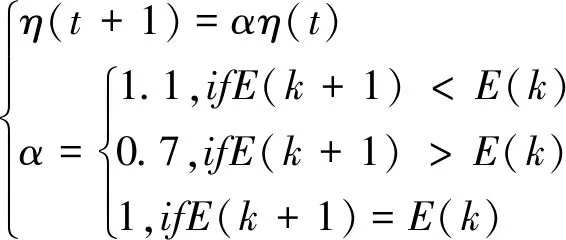
(9)

2.2 数据获取

使用Box-Behnken实验设计法[8]在优化空间内进行抽样，按照抽样点对应的参数对汽油机活塞进行车削加工，而后测量加工件的表面粗糙度。得到32组实验结果，如表1所示。

表1 实验数据

2.3 训练结果验证

使用式(8)和式(9)给出的训练方法对神经网络参数进行训练，训练完毕后对网络拟合准确性进行检验。将拟合准确性定义为：

(10)

式中：Acc为拟合准确性。

分别计算BP神经网络的拟合精度、经验公式(2)的计算精度，如表2所示。

表2 精度对比

由表2可以看出，BP神经网络的拟合准确度为99.11%，经验公式的计算精度为91.25%，远小于BP神经网络的拟合精度。说明将BP神经网络应用于参数优化。可以得到更加准确的优化结果。

3 多目标优化与决策算法

3.1 多目标优化算法

本文使用融合非支配排序的差分进化算法对多目标优化模型进行求解。多目标优化与单目标优化的区别体现在基于非支配排序的选择过程。

(1)染色体初始化。由于设置了3个优化参数，因此染色体具有3个基因位，即x=(ae,ap,af)。使用随机方式进行初始化，为：

(11)

(2)变异操作。以差分的方式[9]对染色体执行变异操作，即：

xij(n+1)=xOj(n)+F·[xPj(n)-xQj(n)]

(12)

式中：i≠O≠P≠Q；F为缩放因子，n为迭代次数。当变异操作产生的个体超出取值范围时，则重新选择差分个体进行变异。

(3)交叉操作。在变异操作后执行交叉操作，从而提高染色体多样性。对于两个相异的染色体xpj和xOj，交叉操作为：

(13)

式中：rand(0,1)为(0，1)间的随机数，CR为交叉概率。

(4)选择操作。对于多目标优化问题，基于非支配排序[10]和拥挤度因子进行选择操作。其步骤为：首先，将父代染色体和子代染色体进行混合；而后，对混合染色体进行非支配排序；最后，基于非支配排序结果和拥挤度因子[11]对染色体进行选择，保持染色体规模不变。

3.2 多目标决策方法

经过3.1节的求解，得到多目标优化的Pareto前沿解集，那么接下来存在解的选择与决策问题。为了解决这一问题，本文提出了基于加权相对距离的决策方法，具体分为以下步骤：

Step1：目标参数归一化，方法同式(5)，以2维目标参数为例，归一化结果写为矩阵形式：

(14)

式中：N为Pareto解集中解的数量，(z11,z12)为解集中解1的2个目标取值，其余zij含义与此相同。

Step2：设置权重。为相对偏重的目标设置较大的权重ω，得到加权后的矩阵形式为：

本文将2个优化目标视为同等重要，即取ω=1。

Step3：确定理想解与不理想解。所谓理想解是指由各目标最优值组成的解，理论上此解无法实现。所谓非理想解是指由各目标最差值组成的解。以2维最小化目标为例，理想解与最不理想解如图4所示。

Step4：计算相对距离。计算Pareto解集中某解i与理想解、非理想解的相对距离。

(15)

Step5：计算解i的优劣指标参数，为：

(16)

式中：Ci为解i的优劣指标参数，其值越大表示解的质量越高，则选择Ci值最大的解作为决策结果。

4 实验验证

2.3节已经对BP神经网络的拟合精度进行了验证，本节只对多目标优化结果和决策结果进行验证。

4.1 多目标优化求解结果

根据1.1节的实验方案和表1中的实验数据，使用非支配排序差分进化算法对多目标优化模型进行求解，算法参数设置为：染色体规模为60，算法最大迭代次数为500。得到Pareto前沿解集如图5所示。

4.2 多目标决策与对比

按照3.2节的步骤计算Pareto解集中各解的优劣指标参数Ci，所得结果如表3所示。

表3 Pareto中各解的指标值

根据表3的计算结果，选择第17组解作为决策结果。另外，为了对本文的优化方案进行说明，设置了2组比较方案，一是工厂现有加工方案，二是使用经验公式计算结合多目标求解与决策的方法。基于3种生产方案均生产10个汽油机活塞，测量表面粗糙度并计算材料去除速率，对比结果如表4所示。

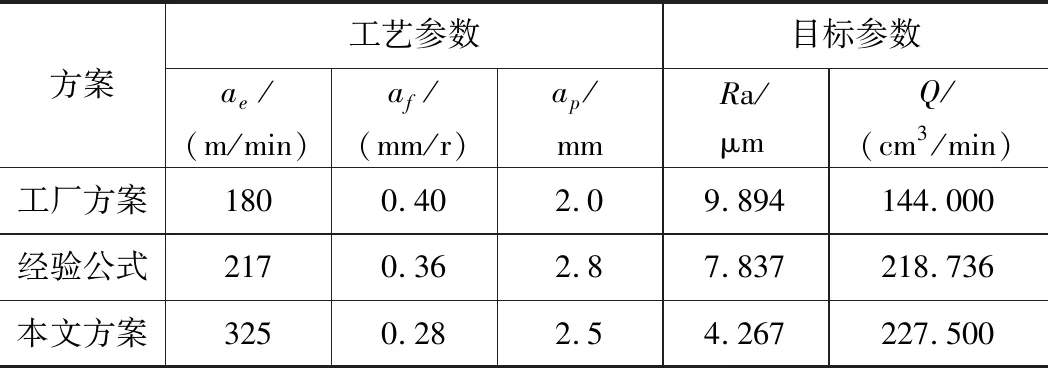
表4 不同生产方案比较

由表4可知，基于经验公式的优化结果在表面粗糙度和材料去除速率2个方面均不如本文的优化结果，这是因为经验公式的计算精度差于BP神经的拟合精度，因此经验公式无法进行高精度的优化，或者说基于经验公式的优化结果可信度小于基于BP神经网络优化的可信度。工厂现用生产方案中，生产工件的表面粗糙度均值为9.894 μm，材料去除速率为144.000 cm3/min，而本文优后生产工件的表面粗糙度均值为4.267 μm，比工厂现用方案减小了1倍以上，材料去除速率为227.500 cm3/min，生产效率提高了57.98%。这是因为工厂的生产工艺确定与优化是基于专家经验给出的，基于专家经验的优化深度有限，且各专家的生产经验区别较大，因此工厂现用的生产工艺差于基于智能算法的优化结果。

5 结语

本文研究了汽油机活塞数控车削加工过程的优化问题，建立了表面粗糙度、生产效率的多目标优化模型，给出了多目标优化与决策算法。经验证得出以下结论：(1)车削加工件表面粗糙度的经验公式计算精度差于BP神经的拟合精度。(2)经过优化与决策，本文给出的生产方案不仅降低了工件表面粗糙度，而且提高了生产效率。