航空叶片电加工多物理场耦合仿真及实验研究

胡宝文 穆瑞元 黄 亮 贾 峰

(①上海卫星工程研究所，上海 200240；②西安工业大学机电工程学院，陕西 西安 710021)

航空发动机技术的进步，对叶片型面加工提出了更高的要求，随着发动机叶片材料和制造难度的升级，传统加工方式制造的叶片会出现部分缺陷。精锻与精铸技术加工过程难以控制，叶片表面容易出现微裂纹等表面损伤，导致次品率较高；数控加工技术在加工高温合金等难切削材料时，刀具磨损严重，易产生表面改性和薄壁件变形，影响叶片最终的使用性能；电火花加工技术电极损耗严重，加工表面会产生再铸层、热应力和拉伸残余应力[1]。

电解加工是基于阳极溶解原理借助成型阴极以离子形式去除材料的工艺方法，将电解加工应用于叶片型面加工有自身工艺的优越性，如叶型成型简单，无宏观切削力，可用于加工薄壁和易变形零件，是制造发动机叶片的理想工艺[2]。但影响电解加工过程的参数较多且涉及多个物理场，各场间相互作用反复迭代，难以人为控制和准确预测，叶片加工精度难以保证。Klocke F[3]等人通过耦合电解加工相关守恒方程，仿真了工件材料去除过程，得出了材料蚀除规律；江伟[4]分析了电场和流场的耦合作用，仿真了脉冲电解加工过程脉间和脉宽跳跃区域内数据的传递，得到加工间隙内各物理场的分布；何长运[5]运用多场耦合模型进行电解加工过程的仿真，并利用管电极电解加工实验验证了模型的准确性；蒋立军[6]建立了电化学加工过程多物理场数学模型，求解了加工区温度和气泡率，并分析了流速和加工电压对电化学加工过程的影响规律。

以上研究中，多场耦合模型简化了耦合过程的相关参数，造成反馈及收敛的数据不够精确，实际加工过程阳极工件型面的预测与实际加工的工件型面出现误差。为解决叶片电解加工型面难以预测的问题，本文进行了多物理场耦合仿真研究，根据电场、流场、温度场特性建立多场耦合数学模型，利用Matlab ode45函数求解模型中各参数沿电解液流动方向数值解；利用COMSOL软件对叶片电解加工过程多物理场进行模拟仿真，得到加工间隙内电解液流速、温度、电解质电流密度等分布规律；完成了叶片电解加工试验，用三坐标测量机得到叶片轮廓曲线的实测值，与单电场仿真的理论值和多物理场耦合后仿真的理论值进行对比，验证多物理场耦合模型的准确性。

1 电解加工多物理场耦合数值解

电解加工涉及多个物理场影响，电场直接影响阳极材料去除，流场和温度场作用于物理量和工艺参数，间接影响阳极工件成型，电导率直接影响着电解加工的平衡间隙，因此得到加工间隙内的实时电导率是提高加工精度的必要所在。

1.1 电解加工各场特性分析

在电场作用下两极间克服了电解液电阻压降，电解液内部自由离子定向移动产生极间电流。假设电极表面均为等势面，根据拉普拉斯方程得电解加工间隙内电位分布关系：

(1)

电解加工成形规律的根本是阳极加工表面的电化学溶解，基于法拉第定律可得出法向平衡间隙计算公式[7]：

(2)

式中：κ为电导率，vaθ为θ处工件的电解速度；δE为阴、阳极压降，一般为1.5～2.0 V。

流场是电场、温度场的载体，是建立电场和温度场的基础，假设电解液为理想状态的连续不可压缩黏性流体，忽略电解产物对电导率的影响，对于封闭的电解液区域气液两相存在各自质量守恒，气液两相的质量连续方程：

(3)

(1-β)Δu=Δ0u0

(4)

根据动量定理可得气液两相动量方程：

(5)

式中：ηg为析氢电流效率；kg为氢气质量电化学当量，β为气泡率，τ为黏性剪切力。

RANSk-ε湍流模型可以满足工程实际的需求，对于不可压缩流体，其湍流动能方程和耗散率方程为[8]：

(6)

式中：k是湍动能；ε是湍动耗散率；Gk是湍动能k的产生项；σk、σε是与k和ε对应的Prandtl数，取值为1.0、1.3；C1ε、C2ε是模型常数，取值为1.44、1.92。

极间温度的变化会影响电流效率、气泡率和金属的钝化，加工间隙内电解液的温度受到电场和流场的相互作用，满足对流-扩散方程[9]：

(7)

式中：Cl为电解液比热容；kt为电解液热导率；Q为加工过程中产生的热量。

电解加工过程涉及到电、流、热传导、化学反应以及结构场等通过场变量、源变量或物性变量之间相互作用，是电场、流场、温度场等多个物理场共同耦合作用的结果，实际电解加工过程中，电导率受到电解液温度和气泡率的影响：

κ=κ0[1+ξ(T-T0)](1-β)n

(8)

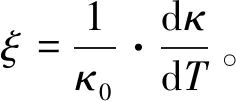
根据控制体中各项能量关系，可以得到能量方程[10]：

(9)

式中：x为电解液流程长度。

1.2 多物理场耦合数值求解

叶片电解加工中，沿电解液流程方向上，取x和(x+dx)两个截面所包围的控制体，利用上文分析的各单场特性，将单场控制方程统一参数并联立，根据电导率这个中间变量实现电场、流场、温度场3场模型联立：

通过求解耦合方程既可得到流速u、压力P、气泡率β、加工间隙Δ、温度T各项参数沿间隙通道的分布规律。为保证更高的精度和数值稳定性，选用ode45函数实现变步长四阶五次龙格库塔算法求解方程，通过多次迭代收敛，可以得到各参数与加工间隙流程的关系，实现多物理场模型耦合模型的数值求解，为清楚观测函数变化规律将Matlab求解的数值代入Origin软件，用Origin将数据重新整合，生成的参数图像如图1所示。

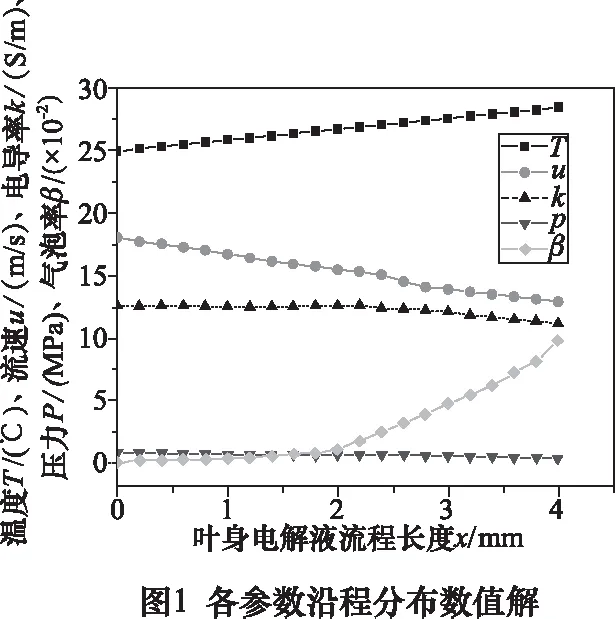
由参数沿程分布图可以看出沿流程气体的体积流量逐渐增加，气泡率沿程增大；电解液压力呈下降趋势，电解液温度线性增加，但因为电解液流程较短，温度升高幅度不大。电导率受气泡率和温度的共同影响，气泡率增加使电解液电导率减小，温度升高导致电导率上升，电导率作用于加工间隙，使之呈非线性分布。

2 叶片电解加工多物理场仿真分析

多物理场耦合指一个系统中两个或两个以上的物理场发生相互作用彼此迭代，改变原有场的基本数值而产生的一种效应或现象。电解加工过程涉及到电、流、热传导、化学反应以及结构场等通过场变量、源变量或物性变量之间相互作用，是多个物理场共同耦合作用的结果。

电解加工过程中，电解液流动从加工开始到结束持续受流场的作用，因此对流场的仿真是分析稳态流场流动问题。流场仿真结构图如图2所示，为保证间隙流场达到要求流速并使间隙流场均匀分布，根据控制变量法得到最优进出口压力组合为入口压力Pin=0.8 MPa，出口背压Pout=0.2 MPa。

极间间隙速度场流线分布图如图3所示，流液为湍流状态，速度流线的长度及方向一致，均匀平缓仅在进口位置叶根和叶尖处出现小范围波动，但流速在间隙内变化较小，出液速度均匀，不存在涡流。

压力分布等值线图如图4所示，流场压力在进口到出口阶梯状均匀减小，不存在突变和局部压力波动，由于轴线上曲率不同，出现不同的压差，但在沿流程方向上不影响间隙流场分布。

电场仿真模型如图5所示，设置二次电流密度初始条件加入电极反应模型表示电极表面的电化学极化作用，需要设置的参数包括交换电流密度，平衡电位，阴、阳极Tafel斜率等，在参数设置中将以上参数分别加入，在求解器中加入电流分布初始化，模拟出加工间隙内的二次电流密度分布。

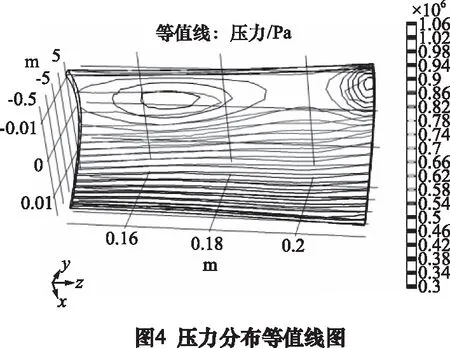
图6为电解质电流密度大小分布云图，电流密度分布较为均匀，仅在进气边叶根处相对较大，平均大小保持在60 A/cm2，无突变和尖端放电现象产生；间隙电解质电位从阳极表面到阴极表面逐渐递减，由于电化学极化的影响，叶片曲率变化较大的区域电位分布平缓。

为定性分析电解质电位变化规律，以及在后续工件型面预测中，为保证计算结果准确的前提下减少计算量，在叶片模型表面选取截面线以及线上控制点，如图7所示。

以上截线中，L2处曲率变化较大，对参数变化影响较大，所以在COMSOL仿真过程中截取L2截面线以及控制点P，对其做主要分析，如图8所示。

叶片电解加工过程多场耦合仿真采用序贯耦合方法，其加工区域耦合求解历程如图9所示，先进行稳态的流场计算，再加入二次电流密度场、共轭传热场完成3场耦合瞬态求解。

电解加工过程多场耦合仿真的参数选取是仿真结果正确与否的关键，由图1所示，已经得到沿电解加工流程多物理场耦合的数值解，气泡率和温度对于电导率的影响是二者的耦合结果，通过对数值解进行回归线性分析，得到耦合场参数沿流程分布的结果，求得耦合场初始时刻电解液电导率为15.23 S/m，其余仿真参数如表1所示。

表1 电解加工多物理场耦合仿真参数

电解加工过程仿真中的瞬态仿真是通过网格的移动和变形来实现的，为了精确定义网格的移动和变形，引入动网格来实现在求解过程中网格的更新与匹配。添加移动网格物理场(ale)来表示阳极边界的变形，为防止网格不连续剖分，添加求解器内置的自动重新剖分网格，设置阴极边界法向匀速进给，法向网格移动速度vn，以上满足溶解速度方程：

(11)

设置阳极法相网格速度vl=0.7ωit，代入多物理场初始参数，完成边界条件设置，对多场模型进行求解。

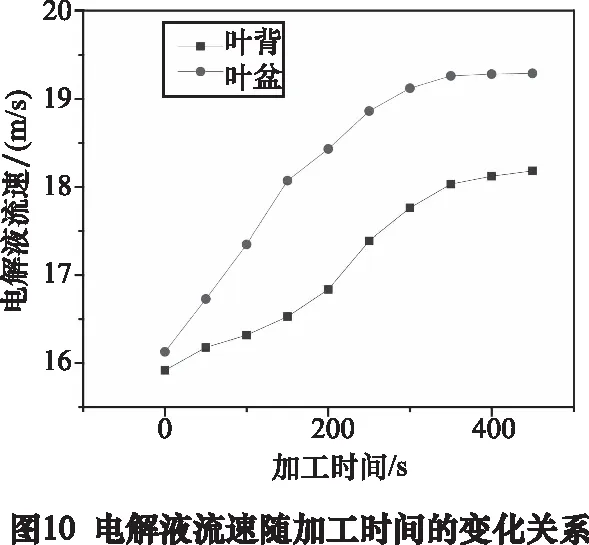
图10为电解液流速随加工时间的变化关系，随着加工时间的变化，加工间隙变小，导致流速变大，加工到380 s左右时，速度变化率不大，证明加工进入平衡间隙。

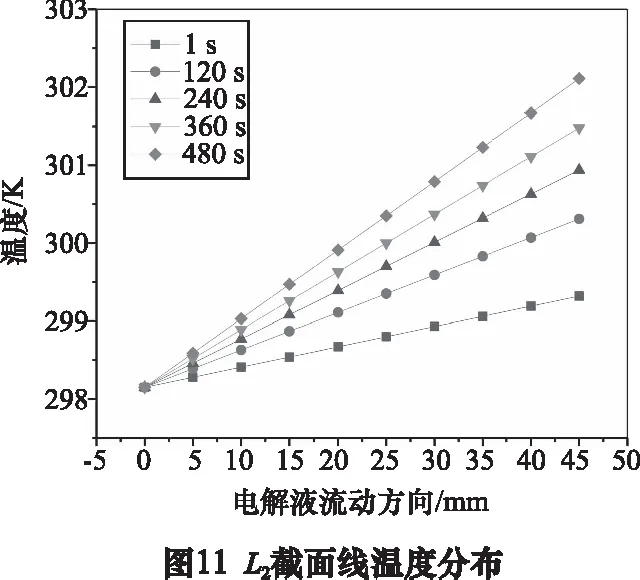
合金材料的电化学分解速率受材料表面温度的影响，因此温度分布间接影响加工间隙，图11为阳极表面L2截面线上温度随加工时间变化关系。由图像可以看出，电解液温度沿流程线性升高，且随着加工时间的增加温度线性变化的斜率逐渐增大，说明极间温度随着加工时间的进行，进出液口处温差变大，流程上温度不均匀。越接近到加工后期，斜率变化率越小，说明加工趋近于平衡，各物理场的相关参数维持恒定。

对叶片电解加工过程进行多场耦合仿真模拟，可有效地研究加工中的各个因素的作用程度，能够对作用参数进行优化，为合理的工艺参数提供指导，有效地缩短工艺试验的准备周期，为叶片电解加工的实际生产提供了科学的指导。

3 叶片电解加工试验验证

3.1 工艺试验

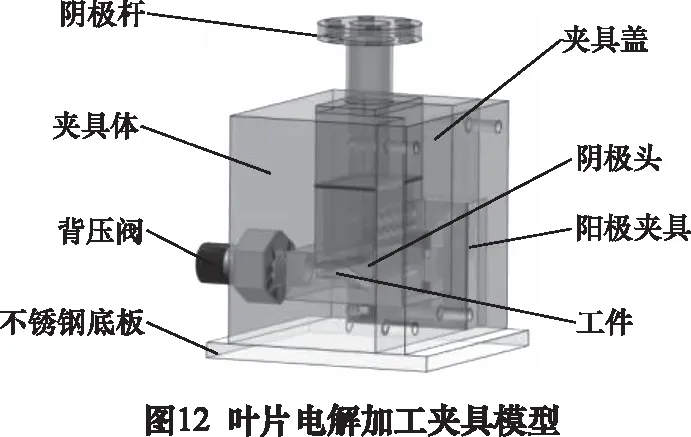
在保证供液充分的前提下，确定加工间隙和阴极进给速度，最后确定电流密度和相应的加工电压，具体试验参数如表2所示。如图12为自行设计的叶片工装夹具，采用单轴立式电解加工机床对涡轮叶片进行电解加工，加工现场如图13。

表2 叶片电解加工试验工艺参数

3.2 试验结果分析与比较

用三坐标测量机对成型件轮廓曲线测量，测量值与理论轮廓差值如图14所示，最大误差0.28 mm，最小误差0.08 mm，叶身模型的平均误差为0.169 3 mm。

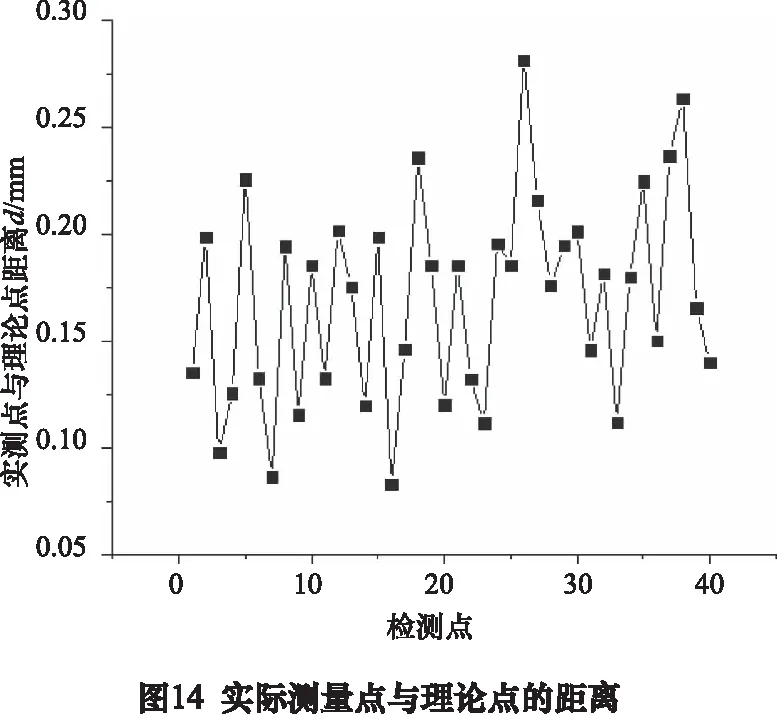
仿真预测的型面轮廓的理论值与试验加工出的工件形貌轮廓实测值对比如图15所示。由图像可以看出：单电场仿真的理论值、多物理场耦合后仿真的理论值与加工试验测得数据值的轮廓趋向基本一致。随着电解液流程的增加误逐渐差变大，多物理场耦合仿真的理论值更接近实际检测值，主要因为单电场仿真认为电导率恒定，未考虑加工间隙温度与气泡率对电导率的影响，仿真结果相差较大。在流程后段实测值腐蚀量比仿真值偏小，造成这种现象的原因是仿真过程默认电解液为线性电解液，而实际的NaNO3电解液为非线性电解液，在电流密度较小时反应停止，随着加工的持续进行，导致仿真结果出现差异。

总而言之，仿真的理论值与实测值有一定误差，但多物理场耦合仿真理论值更接近实际测量值，相比单场理论值能够更加准确地模拟实际电解加工过程，为实际电解加工提供理论指导。

4 结语

为解决叶片电解加工型面难以预测的问题，本文基于COMSOL Multiphisics 软件，在考虑电场、流场、温度场耦合的情况下进行多物理场耦合仿真分析，对叶片电解加工成型件形貌进行准确预测，得到如下结论：

(1)根据数值解函数图像可知，电导率受气泡率和温度的共同影响，气泡率增加使电解液电导率减小，温度升高导致电导率上升，电导率作用于加工间隙，使之呈非线性分布。

(2)温度分布间接影响加工间隙，电解液温度沿流程线性升高，且随着加工时间的增加温度线性变化的斜率逐渐增大，加工后半段温度变化率较小，说明加工趋近于平衡，各物理场的相关参数维持恒定。

(3)仿真的理论值与实测值有一定误差，但多物理场耦合仿真理论值更接近实际测量值，相比单场理论值能够更加准确地模拟实际电解加工过程。

(4)通过实验与理论仿真模型的比较，证明了仿真模型的有效性。