基于变论域模糊控制的风机叶片颤振抑制

王迎博， 易成宏， 孙海鹏， 张晓林， 刘廷瑞

(山东科技大学机械电子工程学院， 青岛 266590)

在来流风速下，叶片所受载荷在气动力、弹性力、惯性力等作用下相互耦合，极易造成气动弹性 问题。气动弹性动态不稳定问题又被称为颤振问题，导致叶片产生一系列大幅度振荡或具有发散特征的挠曲，是风力机叶片断裂损坏的重要原因。经典颤振为发生在势流中的自激不稳定振动流动基本附着无明显分离，由挥舞-扭转耦合产生[1]。随着风力机额定功率不断增大，叶片随之越发细长，如何抑制经典颤振，防止叶片断裂失效，已成为目前研究重点。

针对不同的叶片结构模型，发展了诸多风力机叶片弯扭耦合运动经典颤振研究方法，其中2D典型截面模型由于高效方便，而又能集中分析典型的弯扭发散不稳定振动问题而被广泛采用[2]。Mathieu等[3]基于变桨激励的2D翼型截面弯扭模型，在侧向风作用下通过分析弯扭耦合位移来研究气弹不稳定问题。Don[4]基于弯扭模型进行了兆瓦级风力机叶片的经典气弹稳定性预测，并通过有限元软件进行了验证；Liu[5]基于压电反馈的方式分析单壁复合风力机叶片的经典颤振和主动控制，研究在横向剪切变形、翘曲和二次翘曲耦合作用下，通过压电作用进行风力机叶片的经典颤振抑制。本课题组也曾在前期工作中对2D叶片的弯扭气弹不稳定状态进行了极限环振动分析及智能控制策略的相关研究[6]。

现以叶片保护为目的，通过变桨运动抑制颤振发生，其中变桨动作并非基于传统的功率控制。叶片结构模型采用基于弹簧-质量-阻尼器的典型截面模型，结合经典颤振气动力模型，得到叶片气动弹性方程。变论域最优模糊比例积分微分控制器给出变桨信号，并通过变桨机构执行变桨动作进行叶片颤振抑制。引入的伸缩因子可动态调整论域范围，使系统具有良好的控制效果。

1 结构模型及气动弹性方程

采用大长径比典型截面模型，研究叶片挥舞-扭转耦合振动时域响应。截面模型如图1所示。图1中,截面质量体分别由Z和Y方向的阻尼器、弹簧所悬挂；Z方向为挥舞运动方向；Y方向为摆振运动方向；V为来流风速；α为扭转角；β为变桨角；Fz和Mα分别为气动升力和力矩。

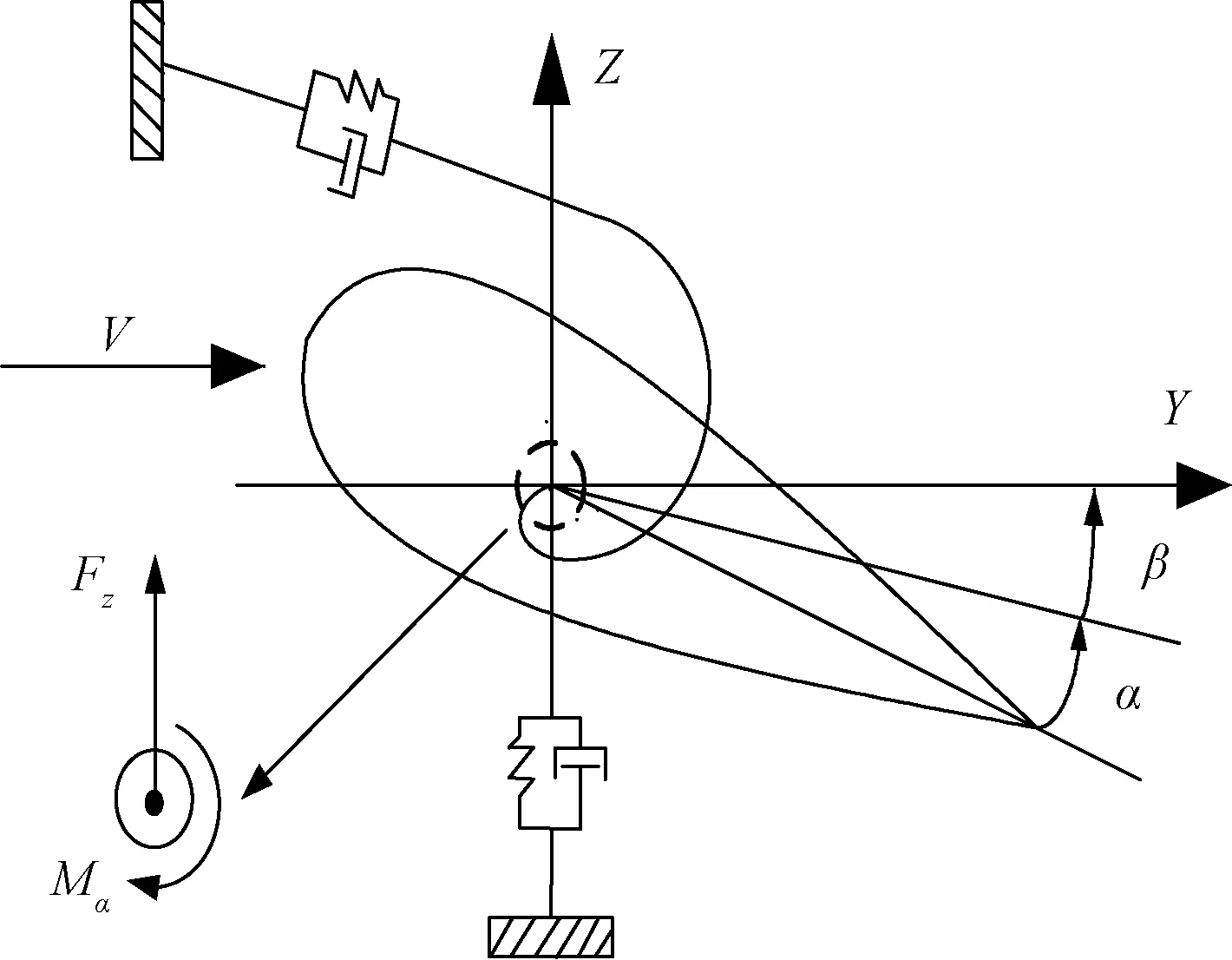
图1 位移坐标及气动力

在不考虑变桨运动前提下，对系统质量项、阻尼项、刚度项求和，将其设置为气动升力产生的总力Fz和力矩Mα，得出力和力矩平衡方程，从而得出二阶微分方程[7]：

(1)

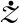
通过升力系数cL和力矩系数cM定义Fz和Mα为

(2)

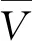
为了便于参数化研究，现进行归一化处理，将方程转换为无量纲形式，定义公式形式为

(3)

以无量纲形式给出上述二阶微分方程：

(4)

为进行颤振抑制，现加入液压变桨执行机构，通过执行变桨动作使颤振逐渐收敛。引入前期设计的二阶变桨激励器[8]:

(5)

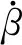
将式(5)与二阶微分方程联立，转换为无量纲形式,得到叶片气动弹性方程为

(6)

由于经典颤振作用在线性流区域，通常在气动力作用下的时域分析即可进行研究[9]。升力系数cL及力矩系数cM可以被定义为

(7)

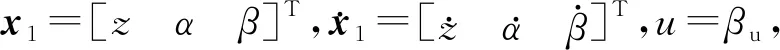
(8)

式(8)中：D为质量矩阵；G为阻尼矩阵；H为刚度矩阵；L为控制向量。

(9)

2 变论域最优模糊PID控制器设计

2.1 气弹变桨模型

基于挥舞误差Δz的变桨PID可以描述为

(10)

式(10)中：KP、KI、KD分别为比例、积分与微分系数。将变桨PID与上述气弹状态方程联立，得到叶片气弹模型：

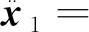
(11)

2.2 变论域最优模糊PID控制

实际风力机叶片系统具有时变、多变量、非线性等特点，通常采用基于模糊逻辑的PID控制器。本文的变桨不是以能量利用为目标，而是以叶片因挥舞-扭转耦合导致断裂失效为主要研究内容，设计出一种变论域最优模糊PID变桨控制器。

普通模糊PID控制的论域范围、量化因子、比例因子等均为固定参数，不能随外界变化而变化。当误差逐渐向零逼近时，模糊规则数量减少，控制精度相应降低，同时控制时间相应延长。针对此问题，李洪兴提出变论域思想[10],通过引入伸缩因子，使论域随着误差的减小而收缩，亦随误差的增大而膨胀，在不改变模糊规则数量的情况下，增加整个系统的控制精度与鲁棒性。包含伸缩因子的基本论域公式为

(12)

式(12)中：t为时间；i为变量，分别表示误差及其变化率；αi、βi分别为输入变量及输出变量伸缩因子；Ei、Ui分别为输入、输出各变量初始论域；Xi、Yi分别为变论域后的输入、输出论域。论域伸缩变化如图2所示，其中，NB、NM、NS、ZO、PS、PM、PB分别表示负大、负中、负小、零、正小、正中、正大，α(x)为论域伸缩因子，E为挥舞误差。

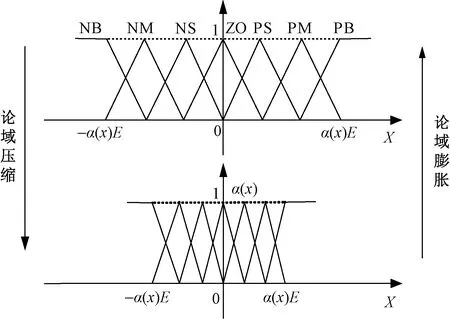
图2 论域伸缩变化图

模糊PID控制器以挥舞误差Δz及误差变化率为输入变量，根据输入变量与PID参数之间的模糊关系设计模糊控制规则，由模糊控制规则实现PID参数的实时整定。基于初值最优化的模糊PID表达式[11]为

(13)

式(13)中：KP0、KI0、KD0为最优化后的初始值；ΔKP、ΔKI、ΔKD为变论域模糊控制的修正值；KP、KI、KD为PID控制器的最终值。变论域最优模糊PID变桨控制器结构框如图3所示，其中，Z0为挥舞额定值，Ke、Kec为输入量化因子，e、ec分别为输入误差及误差变化率，KuP、KuI、KuD为输出比例因子，αe、αec、βP、βI、βD分别为输入输出变量伸缩因子。

图3 变论域最优模糊PID控制框图

2.3 最优模糊PID控制器设计

模糊PID控制器采用双输入三输出的二维Mamdani模糊控制器，以挥舞误差Δz及误差变化率为模糊控制器的输入变量，输出变量为PID控制器的参数修正值ΔKP、ΔKI、ΔKD。挥舞误差基本论 域为[-1,1],误差变化率基本论域为[-3,3]；设定挥舞误差的模糊论域为[-3,3]，误差变化率模糊论域与误差相同，则量化因子Ke=3，Kec=1。输入量语言值分为7个等级，依次为NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大)。输出变量ΔKP、ΔKI、ΔKD模糊论域均为[-3,3],基本论域分别为[-3,3]、[-1,1]、[-1,1],则比例因子KuP、KuI、KuD分别为1、1/3、1/3。输出量采用同输入量相同的语言值等级。为使论域两端过度平滑，当输入输出处于正大、负大状态时采用Z型隶属度函数，其余状态采用灵敏度较高的三角形隶属度函数。重心法可以最大程度利用有效值，得出较准确输出值，故采用重心法进行解模糊运算[12]。

模糊规则为模糊控制器的核心，决定控制器的控制效果。采用“if-then”结构模式，根据专家经验及实际仿真实验得到49条模糊控制规则，ΔKP、ΔKI、ΔKD模糊控制规则如表1所示。

表1 ΔKP、ΔKI、ΔKD模糊规则表

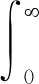
2.4 伸缩因子设计

变论域控制效果主要由伸缩因子决定，输入输出伸缩因子包括基于函数映射和基于模糊推理两种形式[14]。考虑到模糊规则获取困难，因此使用结构简单、控制算法易实现的函数型伸缩因子。函数型输入变量伸缩因子为

α(x)=1-λe-kx2，λ∈(0,1)，k>0

(14)

式(14)中：k为伸缩因子的伸缩速度；λ为伸缩程度。

输出变量伸缩因子为

(15)

式(15)中：kI为比例因子；pi为输入变量权重系数；ei(τ)为输入变量误差；β(0)为输出论域伸缩因子初值。

经过多次仿真计算，输入变量挥舞误差及误差变化率论域伸缩因子分别为

α(e)=1-0.6e-4e2，α(ec)=1-0.6e-4ec2

(16)

考虑到KP、KI、KD数值对控制性能的影响, 输出变量ΔKP和ΔKD的论域伸缩因子与误差的单调性一致,而ΔKi的论域伸缩因子与误差的单调性相反[15]。为此，选取ΔKP、ΔKI、ΔKD的论域伸缩因子分别为

(17)

3 系统仿真及分析

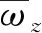
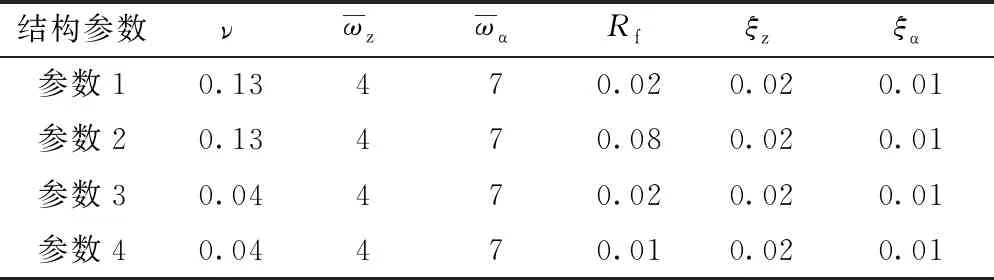
表2 仿真模型参数

给定初始挥舞位移与扭转位移为0.01，根据四组仿真模型参数，在无变桨作用下得到颤振时域响应曲线，如图4所示。

由图4可知，对于挥舞位移和扭转位移，会出现收敛稳定或发散不稳定性的情形。若颤振持续发散，必将导致叶片毁坏，应施加控制以减小振幅。现以参数3颤振发散情况为例，通过所设计的变桨控制器给出变桨信号，并通过液压装置执行变桨动作，对叶片进行颤振抑制。

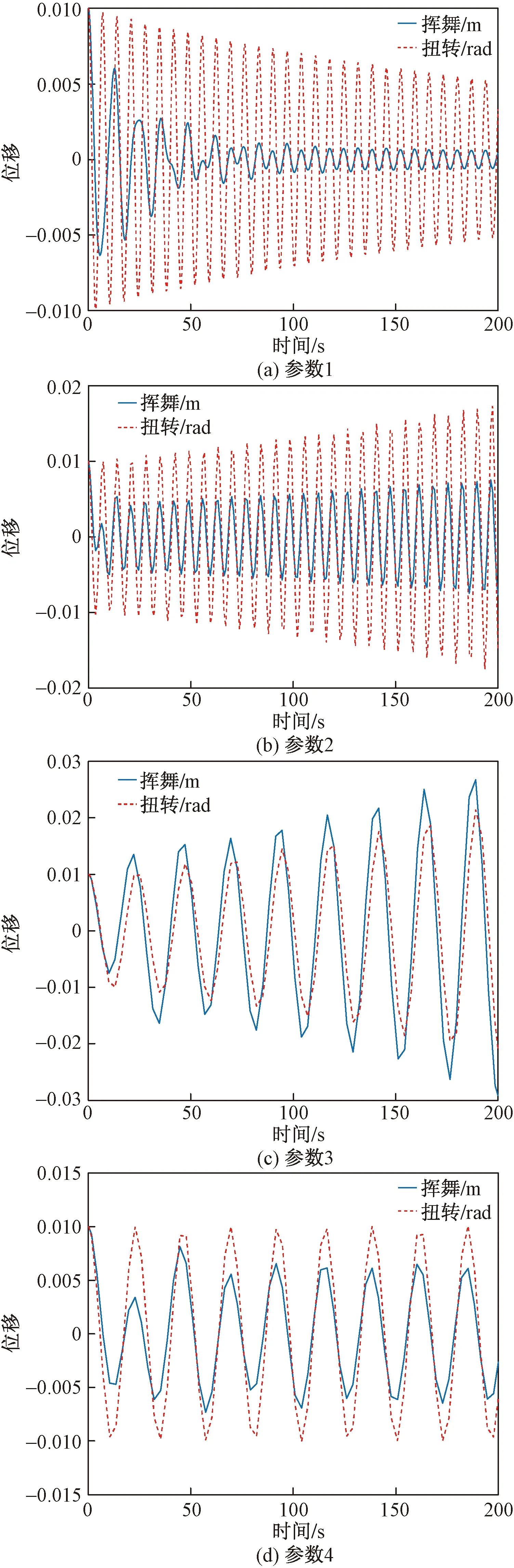
图4 经典颤振时域响应曲线

根据ITAE准则，使用MATLAB中fminunc函数，编程后运行得到系统的最优初始值KP0、KI0、KD0分别为0.25、0.008、1.8。为突出变论域控制效果，加入增量式模糊PID做对比，得到挥舞位移与扭转位移分别如图5、图6所示。

图5、图6仿真结果表明，增量式模糊PID控制与变论域最优模糊PID控制均可使挥舞-扭转耦合颤振由发散状态逐渐收敛。其中，变论域控制最大挥舞位移为未控制的35%，收敛时间为110 s;而增量式模糊PID控制最大挥舞位移为未控制的71%，收敛时间为180 s。对于扭转运动，变论域与增量式模糊PID控制位移基本相等，但增量式模糊PID收敛时间为190 s，变论域收敛时间为130 s，收敛时间缩短30%以上。由此可知与增量式模糊PID相比，变论域最优模糊PID控制器收敛时间快、幅值更低，控制效果优秀。PID参数实时整定过程如图7所示。

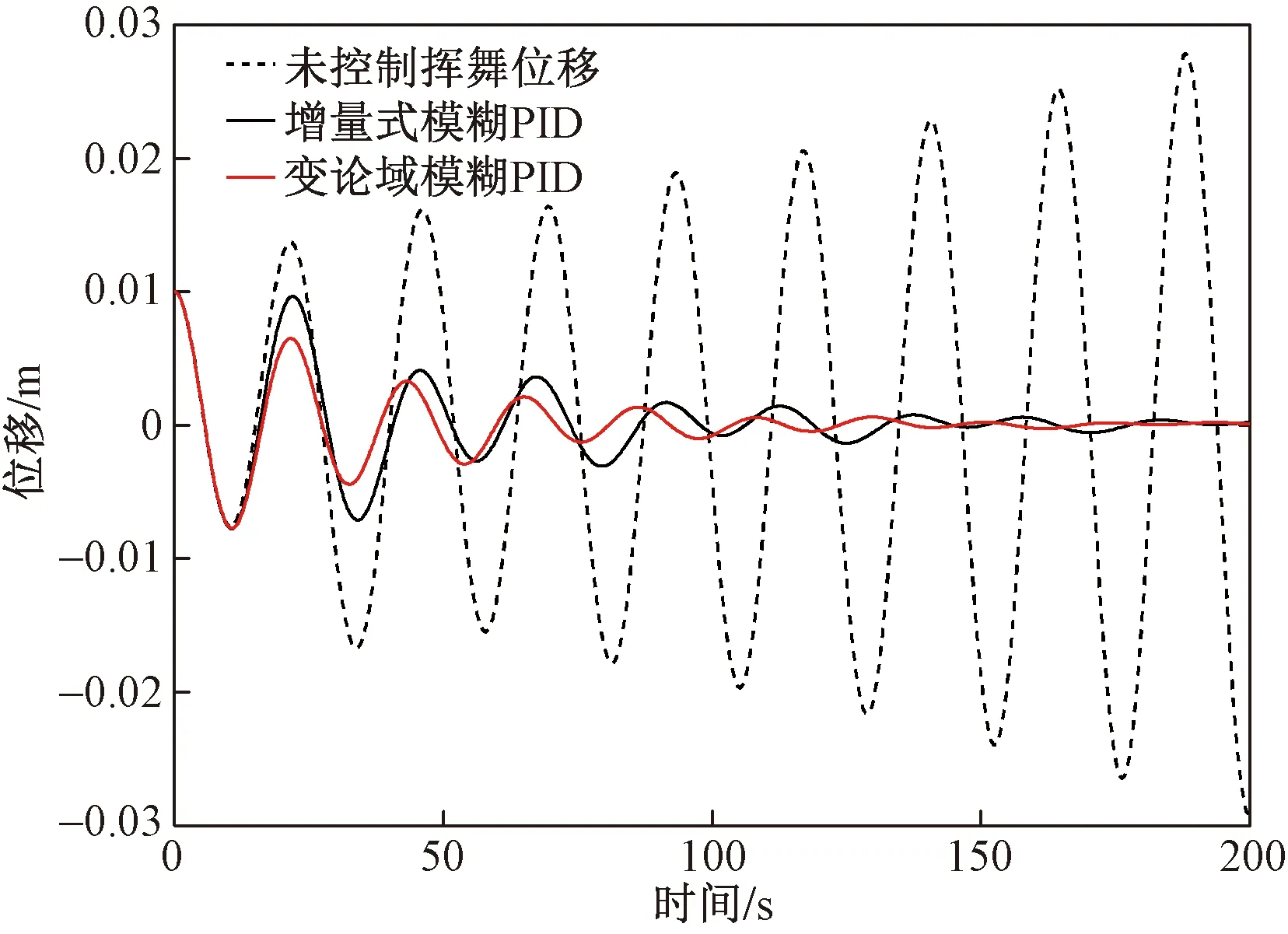
图5 挥舞方向控制效果

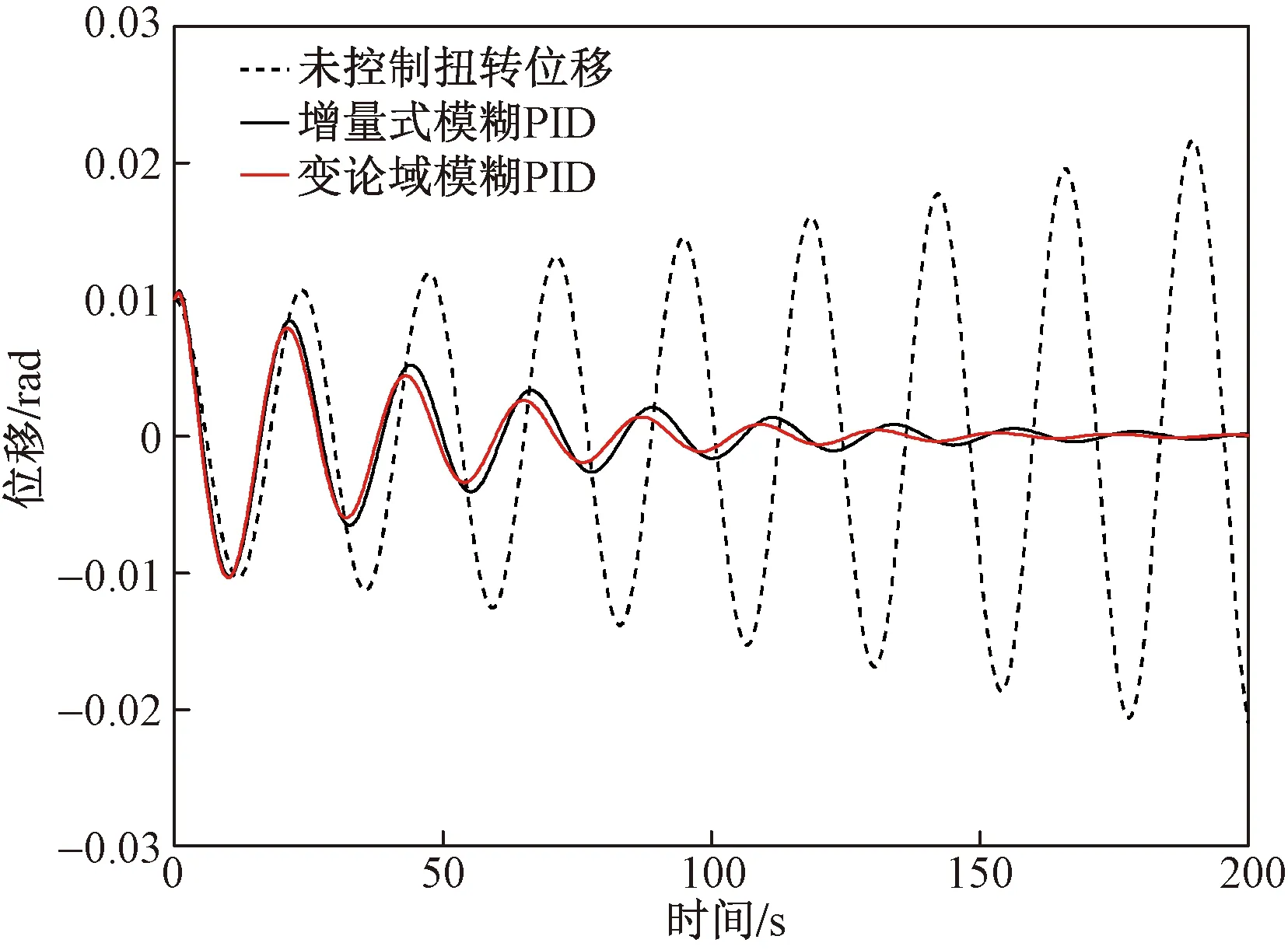
图6 扭转方向控制效果

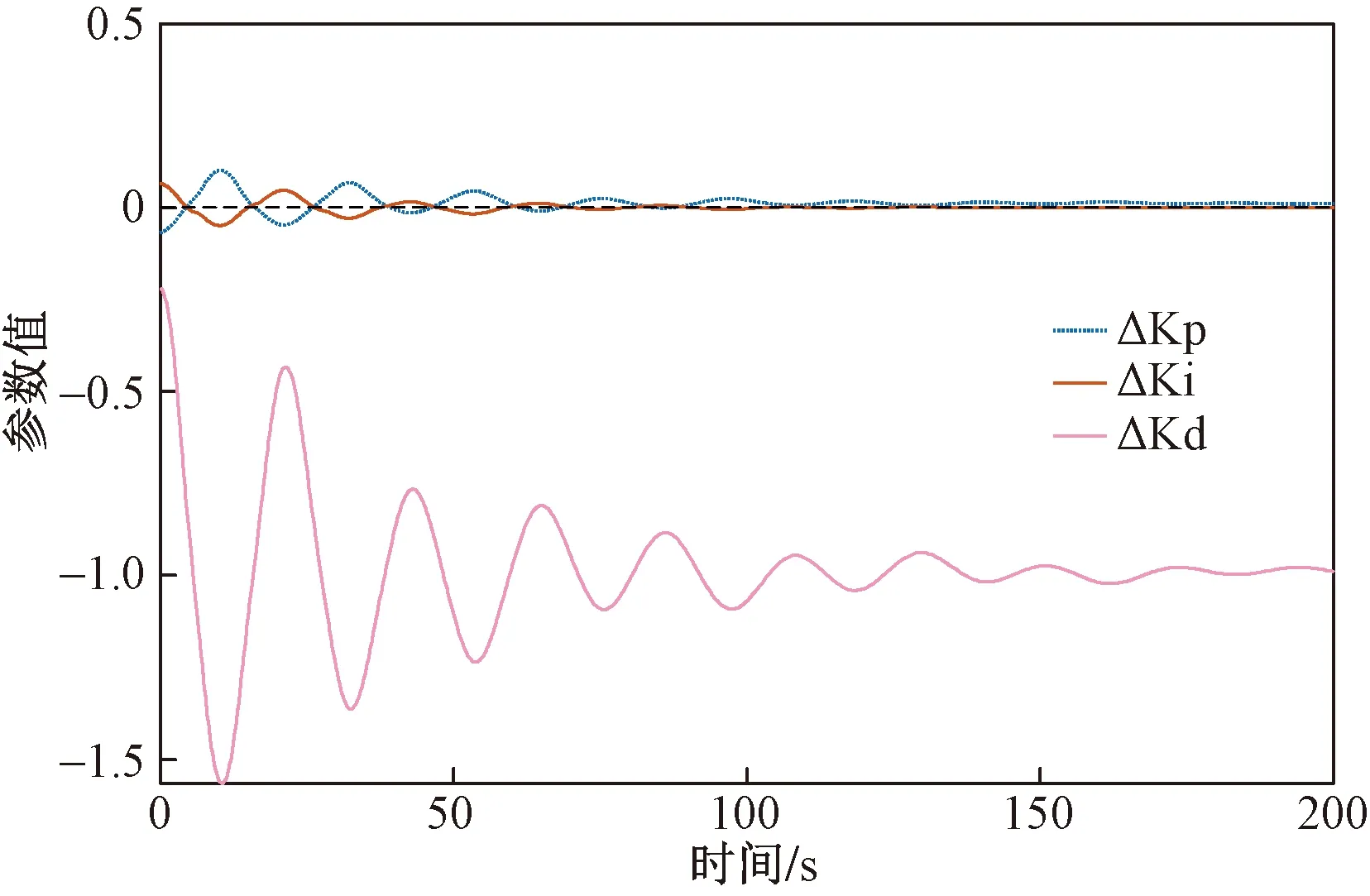
图7 PID参数实时整定曲线

为验证所设计控制器的不失一般性，现对参数2颤振发散情况进行变桨控制。在不改变变论域最优模糊PID控制参数情况下，重复上述控制过程，得到挥舞、扭转、变桨位移曲线如图8所示。从图8可知，在变桨动作下，挥舞运动和扭转运动可在短时间内收敛至稳态。

图8 参数2变论域控制效果

4 结论

(1)针对风力机叶片经典颤振耦合断裂失效问题，将变论域思想与模糊PID结合，设计出一种变论域最优模糊PID控制器。经典颤振研究是在忽略摆振运动基础上进行的，此情况下气动力模型相对简单，但足以说明叶片挥舞-扭转耦合颤振不稳定问题。

(2)变桨动作不同于常规的以功率转换、非线性控制或风能利用为目标，而是以叶片颤振抑制为目的，在颤振发散之前对叶片受迫振动进行控制，以防叶片断裂损坏。

(3)所设计的变论域最优模糊PID控制器结合模糊控制和PID控制的优点，同时变论域伸缩因子可动态调整论域范围，化解了规则数量和控制精度的矛盾，使系统收敛时间更快，幅值更低且具有良好的通用性。