轨道测量装置激光光斑中心定位*

许海翔 李哲一 吴峰崎 龚 文 刘玉明

上海市特种设备监督检验技术研究院 上海 200062

0 引言

传统起重机的轨道测量存在受环境变化影响大、精度低、劳动强度高及安全性较差等缺陷，本文研制了轨道激光测量装置，开发了轨道测量小车及控制分析软件，以实现轨道的自动化测量和数据实时分析。测量装置[1-3]的测试精度由2方面决定：一是测量小车的姿态能够真实反映轨道的空间尺寸变化情况；二是光斑图片的计算中心点能够准确定位激光发射器的中心轴线。前者通过合理设计测量小车的轨道夹紧机构及行走机构保证小车行走姿势稳定可靠；后者根据现场条件等多方面因素设计光斑中心算法，故光斑中心位置是决定轨道测量精度的关键指标。

目前比较常用的光斑中心定位法有质心法、圆拟合法、Hough变换法、空间矩法[4-6]等，这些算法在检测精度、速度和抗干扰性上都存在不足。灰度质心法对于均匀光斑能够较准确定位，计算速度快、抗干扰能力差，对于复杂情况实际图像，定位精度很差，且只能定位中心，不能计算半径。Hough变换圆检测是目前应用最为广泛的方法之一，其可靠性高，对噪声、变形、部分区域残缺、边缘不连续等有较好的适应性，缺点是计算量大，需对参数空间离散化，限制了检测精度。另外，参数空间得票最高的点未必唯一，选择不同点得到的图像空间曲线差异较大。圆拟合法时间复杂度较小，运算的精度较高，算法速度较快，但其抗干扰能力较差。当随机噪声存在时，中心运算精度会明显降低；当遇到很强的外界干扰时，所得到的圆心可能会产生明显错误。在现场测量环境中，由于测距范围变化大，激光光斑存在着散斑、光斑信号强度分布不均匀等干扰因素，仅采用一种光斑中心定位法很难获得理想效果。

本文采用形态级联滤波器和高斯核滤波器对光斑图像进行去噪光滑预处理，为充分利用光斑灰度光强分布特性，采用OTSU算法和最大光强确定阈值区间，以函数进行非均匀阈值分割得到一系列二值光斑图像。在质心法初步确定光斑中心后，对其边缘提取图像进行Hough变换得到一系列中心点样本，然后采用K-means算法获得聚类中心，通过BP神经网络拟合的坐标函数对应关系，求出中心的实际坐标。

2 光斑图像的畸变校正

2.1 测量原理

如图1所示，用激光器发射的激光束作为基准坐标轴，带有光屏的测量小车在轨道上移动，摄像头记录光屏上的光斑图片，并传输至计算机图像处理软件提取光斑中心，换算为小车光屏中心位移，该相对位移即为轨道相对于基准的偏差值，同时记录测量小车行走的位移，经换算生成轨道的空间曲线。

2.2 光斑图像畸变校正

如图2所示，测量小车上装有接收屏和摄像头，摄像头记录激光光斑图像。由于摄像头的鱼眼效应产生了图像桶形畸变，因此需进行畸变矫正，使图像点坐标转化为真实坐标[7]。常用的方法有二元多项式法、神经网络训练及支持向量机法等，其本质都是对坐标转化中非线性函数关系的拟合。神经网络利用其自适应性拟合坐标映射函数，能够有效地完成图像矫正，其泛化能力优于二元多项式法[8]。

图2 测量小车及接收屏

本文采用BP神经网络法对图3畸变图像坐标进行矫正，实际坐标单元格距离为5 mm，建立坐标映射对应关系，其中输入为畸变图像点坐标，点击取点确定10组530×2数据，输出为以o点为原点确定的对应实际坐标，按输入次序重复10组530×2数据，隐含层有2个，节点数分别为5、6。选取9组数据为训练集，1组数据为验证集，通过训练得到网络的权值和阈值，各点预测误差最大不超过0.5。

图3 坐标畸变图像

3 光斑图像中心算法

3.1 图像预处理

本算法流程如图4所示。为便于激光光斑中心的定位和距离计算，采用全站仪测量光屏上确定的坐标点，并构建数学形态学滤波器级联滤波去噪，再进行高斯核函数平滑，完成图像预处理。图5为光斑1预处理不同阶段图像。

图4 算法流程图

图5 光斑1预处理不同阶段图像

3.2 图像阈值的选取

灰度图像采用阈值分割并进行二值化是比较关键的环节，二值化阈值的选取关系光斑中心坐标计算的精确度。OTSU法[9]是最大类间方差阈值方法，将灰度图像按级数分为2个部分，使其之间灰度值差异最大，每个部分灰度差异最小，是图像分割阈值选取的最优方法。在现场测量中，由于测距范围变化大，激光光斑存在散斑、光斑信号强度分布不均匀等干扰因素，需充分利用光强分布特性，阈值区间定义为其中为OTSU法确定阈值，为最大灰度光强值。图6为对光斑1灰度图像分割阈值平面示意，由于所需提取的光斑的中心特性与光强较大部分有关，而与光强较小部分（对应散斑、反射光及背景光等）基本无关。为充分利用光斑光强在不同高度截面分布信息，采用阈值区间内对灰度图像以函数进行非均匀阈值分割，使得光强低的区域阈值分割较疏，光强高的区域阈值分割较密，进而后续光斑中心样本聚类分析能较好地反映中心特性。

图6 光斑1灰度图像

3.3 基于Hough变换的光斑中心计算

Hough变换是一种在图像中定位形状的技术，定义了从图像点到累加器空间的映射，广泛用于提取直线、圆和椭圆[10,11]。光斑图像经阈值区间分割得到一系列二值图像光斑大小也在不断变化，其估计半径在40.7～233.1像素之间。为克服传统的Hough变换计算时间较长的缺点，对二值光斑图像先采用Sobel算子提取边缘图像，搜索半径在估计半径的f20像素范围内，以最大光强面积质心作为初始圆心，圆心累加器在初始圆心的像素范围内计算，以减少Hough变换计算量。为使光斑变形较严重时也能得到正确的结果，对所有搜索半径对应的圆心累加器最大值进行排序，保留后20%区间圆心累加器，经计算得到一系列光斑中心。

3.4 圆心样本的聚类分析

聚类分析将给定的数据分成不同的簇，分类原则是高的簇内相似性和低的簇间相似性，K-means聚类算法是典型的分割迭代算法，即固定K类并根据最小距离准则对样本进行分类。本文对光斑中心坐标样本进行K-means聚类分析计算，从样本点分布情况确定分为3类，并计算每类的质心，将样本数最多的类质心确定为光斑中心。

4 试验结果与分析

4.1 本算法与质心法的比较

为了验证本算法的有效性，将阈值区间非均匀划分为62个二值图像，对其分别进行Hough变换求中心，经中心坐标样本聚类分析后，得到光斑中心图像坐标为(319，149)，其中心图像实际坐标为(322.687 2，151.544 6)，如图7所示。其中三角形为本算法中心，方块为图像实际中心，“.”为62个中心坐标样本点。图8为质心法经聚类得光斑中心图像坐标为(316.052 1，150.023 1)，其中三角形为质心法中心。本算法误差距离为4.48，质心法误差距离为6.81，故本算法精度优于质心法。

图7 本算法聚类中心

图8 质心法聚类中心

4.2 本算法误差情况

为了验证算法的精确程度，再选取光斑2图像进行中心分析，如图9所示。采用本算法参数设置同前，图10为本算法中心坐标(436，150)，真实中心图像坐标为(437.436 5，154.359 5)，分别如图9中三角形和方块所示。将图6和图9光斑图像通过BP神经网络法求得其实际坐标分别为(-0.563 4，15.577 7)、(19.834 5，15.621 1)，屏幕真实坐标为(0，15)、(20，15)，定位误差距离分别为0.81 mm、0.65 mm，2光斑点距离误差为1.99%。其他边缘及中部位置光斑图像进行中心提取如表1所示。

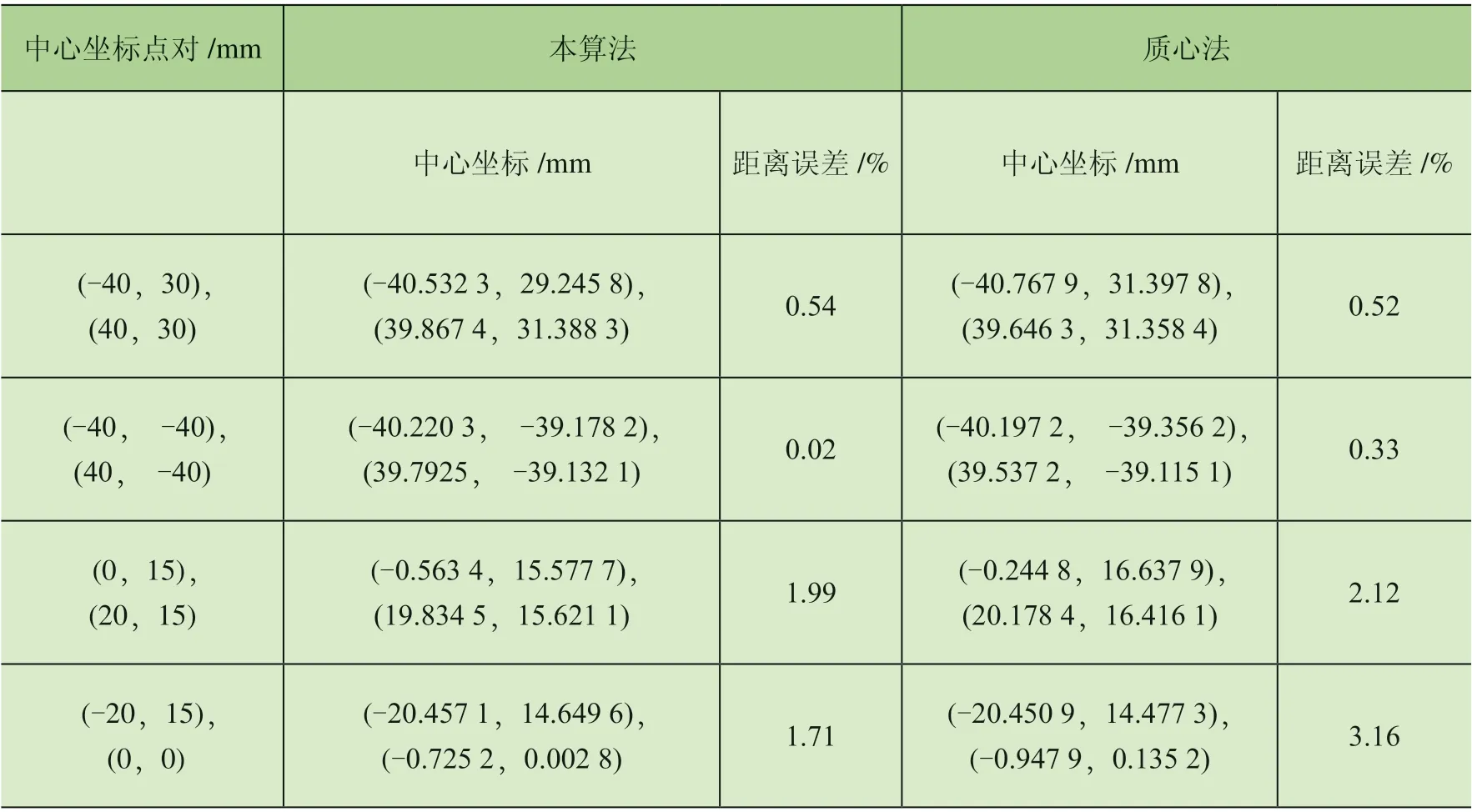
表1 本算法与质心法误差比较

图9 光斑2原图像

图10光斑2聚类中心

5 结论

本文根据激光光斑光强分布的特性，提出了精度满足要求的光斑中心算法。在图像预处理基础上，采用OTSU算法和最大光强确定阈值区间，并进行非均匀阈值分割，充分利用光强较大部分截面能够较好反应光斑中心的特点。系列截面图像光斑中心的提取结合质心法和Hough变换，降低了Hough变换计算量。在本算法框架下，对比质心法和Hough变换获得的光斑中心精度，本算法精度高于质心法，能够满足现场测试的精度要求。本轨道激光测量装置成本低使用便捷，具有较好的推广应用前景。