大型起重船的海流载荷计算方法*
王文浩 王跃齐 周 方
1太原科技大学机械工程学院 太原 030024 2江苏省安全生产科学研究院 南京 210042
0 引言
起重船是海上起重设备,主要应用于造船工程、桥梁建筑、海上救援打捞以及港口装卸等领域。起重船在海上正常作业时,不可避免会受到海浪载荷冲击力,从而导致起重船产生线位移(横荡、纵荡、垂荡)以及角位移(横摇、纵摇、首摇),严重影响船载起重机正常作业,故对起重船在海洋上的水动力分析已成为海洋工程领域的重点。为此,中外众多学者展开了多方研究,Masoud等[1]分析了波浪载荷受波高、波浪周期、船体满载吃水深度以及船体长度的影响,并给出了船体所受波浪载荷的经验公式。在海洋工程设计中,对浮体在海面上的海流载荷外力估算应考虑各种流载荷、流速的垂向分布以及设置海区的实际状况等因素。杨鹏等人[2]根据势流理论和边界元法建立了浮体在水中所受波浪载荷的计算方法。许博方、张少雄等[3]和李英伟[4]依据三维频域线性理论,利用水动力分析软件Sesam对船体进行了波浪载荷直接计算。在分析过程中没有考虑船首、船尾形状以及低速、受限水域的影响。因此,依据海洋工程设计计算理论,本文对3 600 t起重船所受海流载荷作用进行了计算及验证。
1 起重船动力学模型
起重船主要分为船体、吊架、货物3部分。其中吊架部分主要包括臂架、钢丝绳、以及A形架等部件。如图1所示,首先基于有限元理论,运用Ansys软件中的Beam 188单元、Link 10单元和Mass 21单元建立了臂架有限元三维模型。

图1 臂架三维模型图
船体部分简化模型如图2所示,选大地OXYZ为绝对坐标系,坐标系O1X1Y1Z1为随船体移动坐标系,其中船体重心G与随船坐标系原点O1重合。当起重船在海上工作时,会在海浪载荷的作用下产生6个自由度摇荡,船舶重心G分别沿X1、Y1、Z1轴的运动称作纵荡、横荡和垂荡,分别绕X1、Y1和Z1轴的转动分别称作横摇、纵摇和首摇。

图2 船体部分简化模型图
2 海流载荷计算流程图
如图3所示,起重船冲击力分别采用了不同的计算方法,并对起重船排水量进行了估算,最后利用AQWA水动力分析软件对排水量和冲击力进行了计算与验证,得出起重船冲击力计算方法的可行性。

图3 起重船冲击力计算流程图
3 海流载荷计算
在近海工程设计中,若无实测资料则可根据风场观测资料以及相关规范[5]计算出海流流速,即潮汐流速与风海流流速的矢量和等于海流流速。其海流流速随水深变化如图4所示。
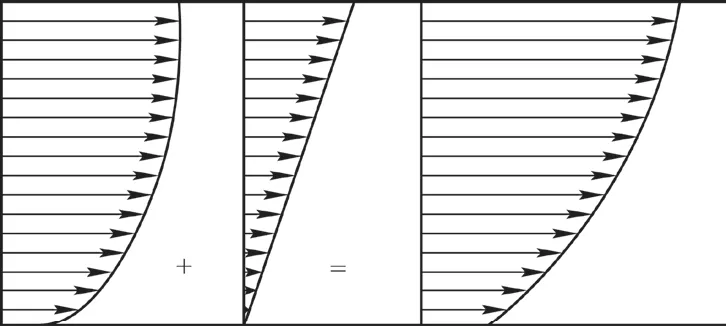
图4 潮流和风海流流速分布
一般地,风海流流速计算公式为

式中:vow为风海流流速;k为系数;一般为0.024~0.05;v为风速。
一般地,海流流速计算公式为

式中:vo为海床以上高度为处的流速,vot为海面潮流流速,vow为风在海面所引起的海流流速,y为海床以上的垂直距离,h为海水深度。
另外,“+”表示风海流速度与潮汐速度方向相同,“-”表示风海流速度与潮汐速度方向相反。
3.1 海流载荷直接计算
当海流单独作用于船舶时,其海流载荷可按流载荷理论[6]进行计算,即
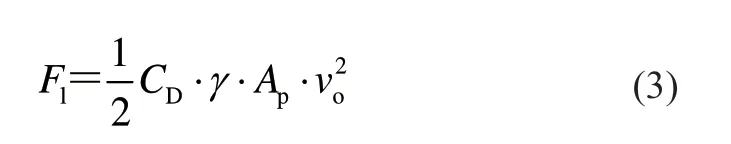
式中:Fl为海流所产生的冲击力;CD为海流拖曳力系数,与雷诺数Re、波浪周期参数KC等有关;γ为海水密度;Ap为船体垂直于水流面的投影面积;vo为海床以上高度为y处的流速。
当考虑波浪与海流同时作用于船体上时,仍可用流载荷理论进行海流载荷计算,即
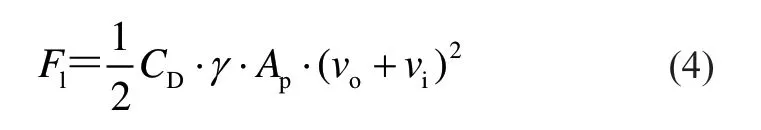
式中:vi为波浪水质点的流速。
根据Airy波理论以及流体动力学理论,可得到t时刻在XY平面的水质点的水平流速vxy,即
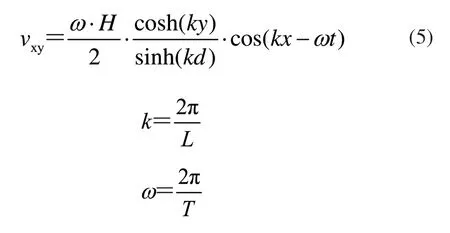
式中:k为波数,ω波频率,T为波周期。
根据Airy波理论,波数k和波频率ω的关系为
式中:g为重力加速度。
在工程应用中,当h/L较小时,椭圆余弦波理论仅适用于浅水波;当H/L较小时,Airy波理论仅适用于深水波;当H/L较大时,则Stokes五阶波理论更为适合。在实际计算过程中,只计算海流载荷作用的情况。
3.2 海流载荷规范计算


式中:Ax、Ay分别为船体外廓的侧面水下面积和正面水下面积,ux、uy分别为通航期内保证率为2%的海流流速之横向分速和纵向分速。
4 海流载荷两种计算与比较
海流载荷主要计算横向和纵向海流载荷对船体产生的水平冲击力,主要情况有船载起重机在正常工作状态下起吊3 600 t货物;船载起重机处于非工作状态。
本文主要对第一种情况进行计算与比较,以3 600 t大型起重船为例,该船的长度为98 m,宽度为24 m,型深为6.5 m,满载吃水4.8 m,海水密度为1 025 kg/m3,取海况为5级蒲福风力。
4.1 排水量及重量估算
排水量计算公式为
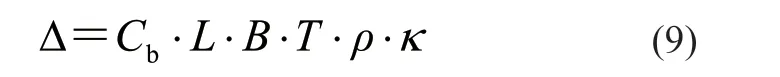
式中:Cb为方形系数,通常取0.8;ρ为海水密度,ρ=1.025 t/m3;κ为型体积系数,取1.005。
根据上式计算出排水量Δ=9 303.8 t。
将起重船系统分为船体、吊架、货物等3个部分,则排水量为

式中:WB为船体质量(包括船上所有设备及物品等);WT为吊架质量(包括吊钩、绳索及吊装设备等);经Ansys分析计算得,WT=2 027.2 t;WC为货物质量,WC=3 600 t。
变换式(10)可得
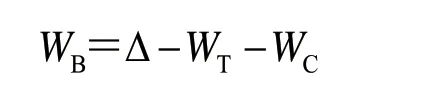
由此,计算出船体质量WB=3 676.6 t。
4.2 起重船的冲击力计算
风引起的水面海流流速为
vow=k·v= 0.03× 1 0 =0.3 m/s
式中:风速v可查阅文献[8]得到。
取水面的潮汐流速为vot=0.5 m/s。
1)当风流速度与潮汐速度方向相反时洋流流速为

产生的横向冲击力为

规范计算得

产生的纵向冲击力为

规范计算得

2)当风流速度与潮汐速度方向相同时
此时,海流流速将达到最大值,即有

此时对应最大横向水平冲击力为

规范计算得

产生最大纵向冲击力为

规范计算得

4.3 两种算法的比较
通过直接计算起重船所受的海流载荷,与规范计算海流载荷进行比较,其中横向及纵向冲击应力值相差1.1 N/m2,最大横向及纵向冲击应力值相差17 N/m2,充分验证其公式的适用性。具体对比结果见表1。

表1 两种方法比较结果
5 通过AQWA水动力软件进行验证
5.1 AQWA
AQWA是一款海洋工程水动力分析软件,能分析浮体在环境载荷作用下的动态响应、海上安装作业、系泊定位、船舶航行及波浪载荷计算等方面问题,计算精度高,操作界面友好,已成为当前许多海洋工程中重要的浮体分析工具之一。
5.2 分析流程
1)建立分析项目
为减少海上航行阻力,将船体水线以下部分首尾削斜,满载时船尾水线以下削斜45°,船首削斜30°,如图5所示。

图5 船体模型
2)定义水线面
将船体模型移动到XY面以下4.8 m处,再将模型以XY面为切割基准面进行切割,最后为防止后期划分网格失败,将船体上下部分建立新Part,如图6所示。船体模型的前处理工作已经完成,开始进行有限元网格建立。

图6 水线切割后的模型
3)定义转动惯量
在AQWA中的船体Part需要输入基于重心的转动惯量,对于规则船舶,根据表2数据计算得到。
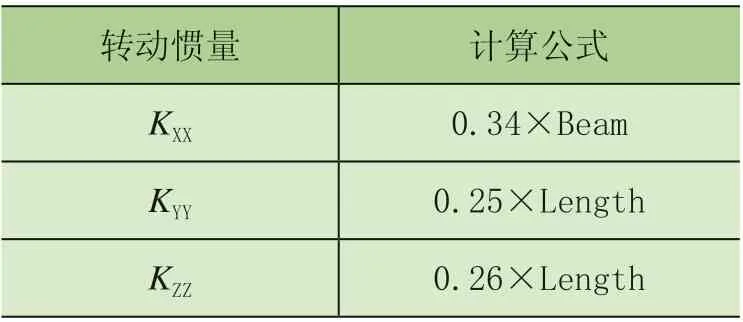
表2 转动惯量计算公式
4)划分网格
将网格破坏公差设置为0.5 m,最大单元尺寸设置为1 m,点击生成网格。其网格划分结果如图7所示。

图7 网格划分结果
5)定义波浪
以大地为绝对坐标系,将海浪速度设置为0.2 m/s,其海浪方向设置为90°,如图8所示。分别设置最低周期和最短周期为25和15,即完成所有参数设置。

图8 定义波浪方向
5.3 分析结果
最后进行求解,得到该起重船排水量为10 456.7 m3。海流方向为90e时起重船面板应力分布如图9所示。

图9 海流方向90°时船体的应力分布
将步骤5中海浪方向改为0°,其他参数保持不变,再次进行求解,得到海流方向为0e时起重船面板应力分布如图10所示。

图10 海流方向0°时船体的应力分布
6 结论
本文给出了基于3 600 t起重船的海流载荷横向和纵向冲击力的计算方法,为起重船的结构设计以及稳定性计算提供了理论依据。通过分析得到以下结论:
1)通过计算实例表明,由规范计算得到的海流载荷比直接计算的结果偏小。对于常规尺度的起重船,进行海流载荷直接计算是必要的。
2)通过AQWA水动力分析可知,起重船满载排水量与计算结果相近,且上述起重船所受海流载荷冲击力计算结果在报告结果最值范围之内,再次验证该船体海流载荷计算方法具有较高的可信度。

