史嗣荣：初中数学教学中数形结合思想的应用

史嗣荣

摘要：数形结合是一种常用的数学思想，将其应用在数学教学中，有助于深入理解知识，促进思维发展。从数形结合思想的应用价值出发，分析了初中数学教学中数形结合思想的实践应用，以供参考。

关键词：初中;数学教学;数形结合;应用价值

数量和图形是组成数学的两个要素，而且这两个要素之间是有联系的[1]。数形结合，就是利用数量的精确性，表达图形的某些属性;或根据图形的几何直观性，表达数量之间的关联。初中数学教学中，对于某些复杂的概念和问题，可以引入数形结合思想降低学生的理解难度。

一、数形结合思想的应用价值

在初中数学教学中，数形结合思想的应用，一方面能方便学生理解数学概念，例如引导学生理解相反数、绝对值、集合等知识点，相比于教师口头讲解的效果更直观。另一方面有助于解决实际问题，尤其是函数、方程、解析几何和立体几何等，数形結合是一种有效的解题方法。

二、初中数学教学中数形结合思想的实践应用

1.以形助数

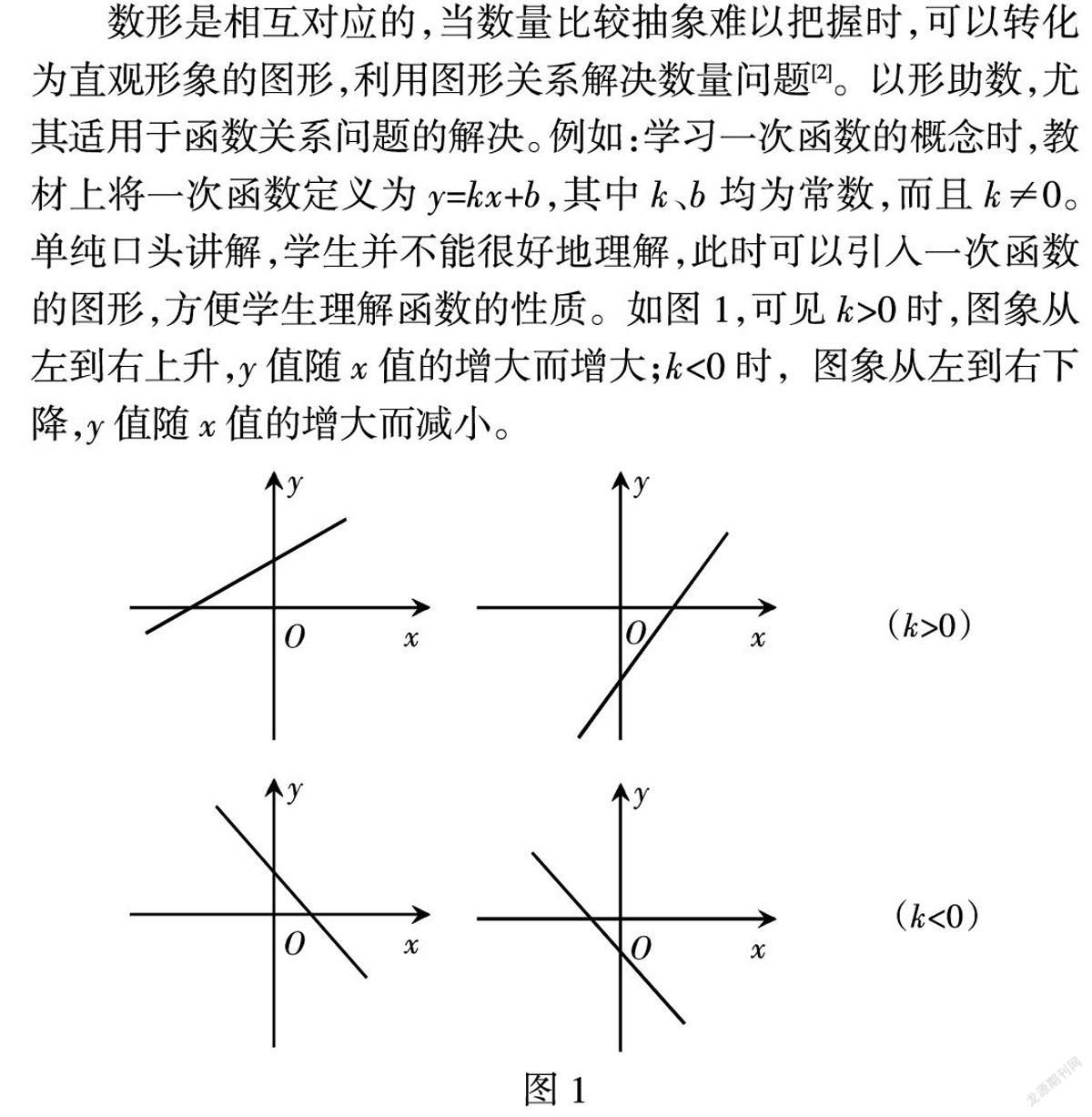
数形是相互对应的，当数量比较抽象难以把握时，可以转化为直观形象的图形，利用图形关系解决数量问题[2]。以形助数，尤其适用于函数关系问题的解决。例如：学习一次函数的概念时，教材上将一次函数定义为y=kx+b，其中k、b均为常数，而且k≠0。单纯口头讲解，学生并不能很好地理解，此时可以引入一次函数的图形，方便学生理解函数的性质。如图1，可见k>0时，图象从左到右上升，y值随x值的增大而增大;k<0时，图象从左到右下降，y值随x值的增大而减小。

例题：已知函数y=3x2+6图象上，有A（-1，y1）、B（-3，y2）、C（2，y3）三点，比较y1、y2、y3的大小。解答这个题目时，可以将x=-1、x=-3、x=2分别代入函数，然后求取y1、y2、y3的值并比较。基于数形结合思想下，可以发现函数y=3x2+6中常数b=0，即图象的对称轴是y轴。当x=0时，此时y值最小为6;随着x值逐渐增大或逐渐减小，y值会相应逐渐增大。因此，在本例题中，x=-1时的y值最小，x=-3时的y值最大，x=2时的y值居中，最终得到答案：y1

2.以数解形

虽然图形比较形象、直观，但定量计算时要依靠代数，尤其是比较复杂的图形，应观察图形特点，发现题目中的隐含条件，利用图形的性质或意义，用数量正确表示图形，从而解决问题。

例题：图2是由4个全等的长方形拼成的图形，根据中间空白部分面积的不同表示方法，写出一个关于a、b关系的恒等式。解答这个题目时，采用以数解形法，刚好是对平方差公式的倒导。即：中间空白部分，可认为是边长为（a-b）的正方形，面积表示为（a-b）（a-b）;也可以看成是边长为（a+b）的大正方形，与4个长方形的面积之差，面积表示为（a+b）2-4ab。因此，a、b关系的恒等式是：（a-b）2=（a+b）2-4ab。

3.数形互变

数形互变，就是数量和图形之间相互转化、多次转化，从已知和结论同时出发，分析并找出内在的数、形互变关系。

例题：如图3，已知E、F是边长为4的正方形ABCD的边BC、CD上的点，且CE=1，CF=4/3，直线FE交AB外延线于点G，选择FG上的一个动点H，作HM⊥AG、HN⊥AD，HM取值为多少时，矩形AMHN的面积最大？解答这个题目时，首先以数解形，从图形中的得到数量关系。假设HM=x，矩形AMHN的面积为y，根据已知条件可得EP=BC-CE-HM=3-x。因△FCE∽△HPE，所以FC/PH=CE/EP，PH/PE=CF/CE=4/3，PH=4/3（3-x），AM=AB+PH=4+4/3（3-x）=8-4/3x，矩形AMHN的面积表示为：

y=HM·AM=x（8-4/3x）=-4/3x2+8x，0≤x≤4

然后以形助数，画出二次函数的图像，可知对称轴为x=3，图像开口向下。x在[0，4]区间内，当x=3时y值最大，此时y=12。即：当HM取值为3时，矩形AMHN的面积最大为12。

三、结语

综上所述，数形结合是一种常用的数学思想，将其应用在初中数学中，能方便学生理解数学概念，有助于解决实际问题。文章从以形助数、以数解形、数形互变三个方面，结合例题分析了数形结合思想的具体应用，希望为实际教学活动提供借鉴，切实提高教学成果。

参考文献：

[1]陈仁忠.基于数形结合思想的初中数学教学研究[J].读与写，2021，18（7）：170.

[2]赖海市.数形结合思想在初中数学教学中的渗透[J].科教导刊-电子版（上旬），2021（1）：207-208.