长期荷载作用下钢竹组合柱的力学性能

张家亮, 童科挺, 陈 伟, 王建民, 李玉顺

(1.宁波大学 科学技术学院, 浙江 宁波 315300; 2.宁波大学 土木与环境工程学院, 浙江 宁波 315211; 3.青岛农业大学 建筑工程学院, 山东 青岛 266109)

钢-竹组合结构是一种新型的组合结构形式,主要由竹材人造板和冷弯薄壁型钢通过结构黏合剂或结构黏合剂-自攻螺钉复合而成,能够充分发挥薄壁型钢强度高、自重轻、延性好与竹材速生强韧、经济环保、比强度高的优势[1].目前,本团队已经对构件力学性能[2]、抗震性能[3]与钢-竹界面黏结滑移[4]等内容进行了大量的研究分析,而有关长期荷载作用下构件力学性能的研究鲜有报导.

目前,国内外诸多学者对木材的蠕变性能展开了研究,但有关竹材蠕变的研究相对较为鲜见.Bažant[5]、张晓敏等[6]和闫薇等[7]分别对木材和竹材的蠕变行为进行了研究,提出了考虑温湿度的木材本构关系,分析了竹材蠕变性能的影响因素.Pierce等[8-14]分析了木质板、竹材刨花板、竹胶板蠕变特性的影响因素,验证了Burger模型拟合蠕变行为的有效性,其精度满足工程需要.Wood等[15-18]以加载水平与持荷时长为基本参数,对多种截面木梁进行了长期加载试验,揭示了构件强度与加载时长的关系,分析了跨中挠度的变化规律,发现通过指数方程与Burger模型描述木梁蠕变行为具有良好的适用性.肖岩等[19]和董春雷等[20]分别对胶合竹梁和竹木复合梁的蠕变性能进行了评价,分析了构件力学性能的变化规律,证明竹木复合梁的蠕变符合木质材料的一般蠕变特征.

鉴于钢材与竹材之间具有良好的组合效应,钢-竹组合工字形柱(以下简称组合柱)的蠕变特性必然与单一竹材有所差异.本文通过组合柱的长期加载试验以及长期加载结束后的二次加载试验,研究长期荷载作用对组合柱变形特性和承载力的影响规律,以期为钢-竹组合结构的后续研究及其在实际工程中的推广应用提供理论依据.

1 试验

1.1 试验概况

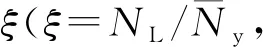
表1 试件参数

图1 试验试件Fig.1 Test specimens

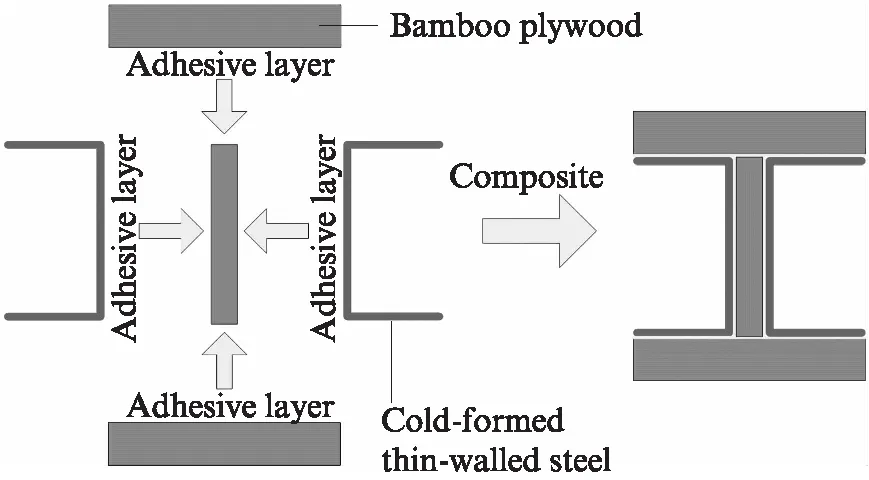
图2 钢-竹组合柱截面Fig.2 Cross section of steel-bamboo composite column

依据GB 1927～1943—2009《木材物理力学性能试验方法》,对6个竹胶合板试样进行轴压试验,测定竹胶合板的抗压强度与弹性模量,结果如表2所示.依据GB/T 228.1—2010《金属材料拉伸试验 第1部分：室温试验方法》对9个冷弯薄壁型钢试样进行拉伸试验,测定屈服强度、极限强度、弹性模量与泊松比,对同一厚度试样测试结果取平均值,结果如表3所示.

表2 竹胶合板力学性能

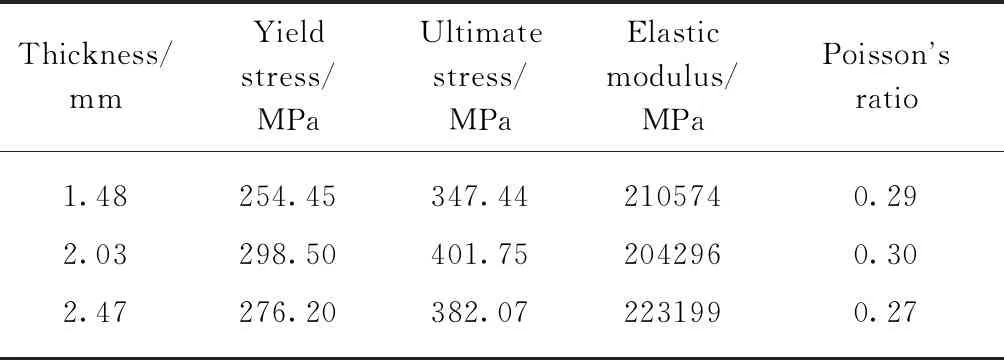
表3 薄壁型钢力学性能

1.2 长期加载试验

1.2.1长期加载试验参数

在实施长期加载试验之前,对9根组合柱一次加载试件进行轴心受压试验,以确定长期荷载施加值,一次加载试验屈服承载力如表4所示.本文采用2种方法确定组合柱试件的屈服荷载试验值：当组合柱上任一薄壁型钢应变片测量数值达到屈服应变或荷载-位移曲线出现明显转折点时,即认为组合柱屈服.两者以先到者为准,将对应的荷载定义为屈服承载力.以加载水平与含钢率为基本参数,对6根组合柱试件实施长期加载试验.

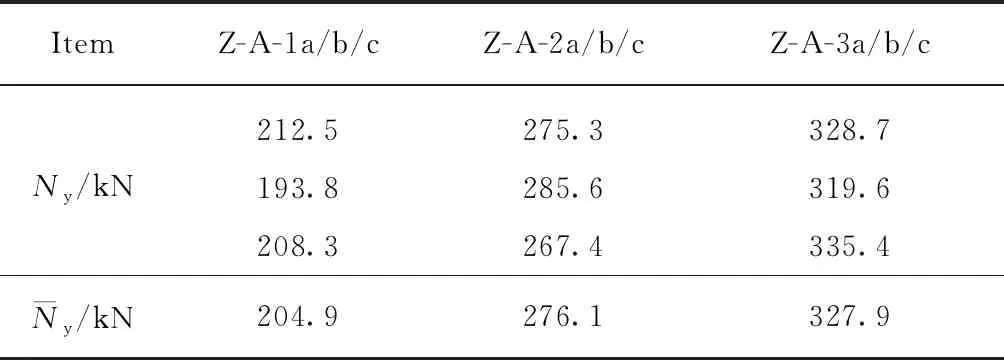
表4 一次加载试验屈服承载力

1.2.2长期加载试验装置

长期荷载的施加和保持是长期加载试验的关键所在,考虑到试验中施加的长期荷载值较大,故不宜采用堆积重物的方法.本文在相关试验研究的基础上,提出了用于构件长期持荷试验的自平衡加载装置设计方案,该装置具有构造简单、传力明确、节约场地等优点.如图3所示,为满足2种荷载水平的持荷要求,共设计了2种加载装置,其中单弹簧加载系统适用于加载水平ξ=0.30的试件,双弹簧加载系统则适用于加载水平ξ=0.56的试件.

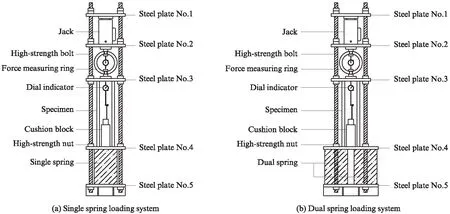
图3 长期加载装置示意图Fig.3 Schematic diagram of long-term loading device

长期加载系统由弹簧、高强螺栓、液压千斤顶、加载钢板、测力环等组配而成.本装置所用弹簧劲度系数为1kN/mm,螺栓为8.8级M30高强螺栓,液压千斤顶最大推力为300kN;加载钢板厚度为25mm,按自上而下的顺序将钢板编号为1～5,部分钢板表面设有加劲肋以提高其刚度;测力环的量程分为200kN和300kN 2种,分别用于监测单弹簧加载系统与双弹簧加载系统的长期荷载实时数值.加载前,在万能试验机上对测力环进行3次预压,预压荷载分别为2种测力环对应量程的50%与70%.

1.2.3试验方法

长期荷载施加值NL由加载系统的测力环测量,测力环读数便捷且能够实时读取NL的变化.为准确有效地监测组合柱试件的长期变形,试验包含2部分形变测量内容：在4号钢板上布置了与3号钢板相连的千分表,以测量蠕变变形;在距离组合柱上下端部150mm处和柱中部位,分别布置了12个应变测点,以测量组合柱在持荷期间的应变.

长期荷载的施加现场如图4所示.施加长期荷载NL的步骤如下：(1)将组合柱放置在加载系统的4号钢板上,并进行几何对中;(2)安装测力环与千分表,连接应变采集设备;(3)使用液压千斤顶对组合柱进行预压,确保位移和应变数据准确采集;(4)采用分级加载的方式施加长期荷载,每级荷载为NL/4,当测力环读数达到NL/4时,均匀地拧紧2号钢板上的8个螺母,此时即完成了第1级荷载的施加,以此类推可进行第2、3、4级荷载的施加;(5)长期荷载施加完成时,立即记录各个组合柱的初始变形和应变.

图4 长期荷载施加现场Fig.4 Applying long-term loads on site

随着试验进程的不断推进,构件将发生蠕变变形,同时被压缩的加载弹簧有所回弹,导致测力环读数有所下降.为保持组合柱长期荷载施加值NL的恒定,使用千斤顶进行补充加载.在组合柱长期加载的前60d,蠕变变形明显,测力环读数降幅较为显著,需要每隔5d左右对加载系统进行一次补载;随着加载时间的延长,蠕变变形增幅放缓,测力环读数较为稳定,每隔15d左右补载1次.

1.3 二次加载试验

在为期235d的长期加载试验结束后,将6根组合柱试件从长期加载装置上卸载,随后立刻在电液伺服万能试验机上进行二次加载试验,如图5所示.二次加载试验采用力控制分级加载方案,加载速率为0.4kN/s,每级荷载增量为10kN,每级荷载持荷时长30s.在距离组合柱上下端部150mm处及柱中截面处布置应变片,以测量组合柱在轴心荷载作用下的应变,应变数据采用DH3816静态应变测试仪采集.

图5 长期荷载卸载后的二次加载试验Fig.5 Secondary static loading test after long-term loading

2 长期加载试验结果与分析

2.1 试验环境

长期加载试验共历时235d,在监测试件变形的同时,记录试验所处环境的温度与湿度,其中试验温度随时间变化幅度较大,最大温差达30.9℃.为使试验结果更加可靠,本文考虑了温度对组合柱蠕变变形的影响并制作了3个温度测试试件(TM-1～TM-3),以研究温度对组合柱变形的影响规律.具体实施方案为：将温度测试试件自由、竖直地放置在进行长期加载试验环境中,确保温度测试试件与长期受荷试件所处环境温度相同;在温度测试试件中部对称布置4个应变片,以测量组合柱因温度变化而产生的变形;考虑温度升高或降低对试件纵向变形的影响,对试件长期变形量测结果进行修正.长期加载试验期间,试验环境相对湿度保持在70%左右,随时间变化幅度较小,故本文未考虑相对湿度对组合柱蠕变的影响.

2.2 蠕变-时间关系曲线

通过对6根组合柱进行为期235d恒定荷载作用下的加载试验,得到了在不同加载水平下的蠕变变形.为清晰展示构件蠕变过程,未考虑组合柱在长期荷载作用下初始变形的蠕变变形-时间(Dcr-t)关系曲线如图6所示.由图6可见：在长期荷载作用下,组合柱蠕变变形的增长较为明显;加载初期,组合柱的蠕变速率较快,加载至30、60d时,组合柱的蠕变量分别占总蠕变量的75%和90%左右;加载100d之后,组合柱变形发展缓慢,蠕变变形曲线渐趋水平.

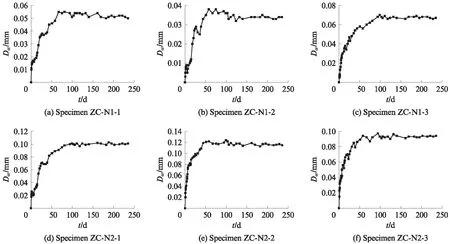
图6 未考虑初始变形的蠕变变形-时间曲线Fig.6 Creep-time curves without considering initial deformation

通过对蠕变数据的进一步分析可知,各试件在90d内的蠕变变形大小关系依次为D30-Di>D60-D30>D90-D60,其中Di为初始变形量,D30、D60、D90分别为持荷30、60、90d时的蠕变变形.由此可知,组合柱的蠕变速率随时间的延长而降低.

2.3 蠕变分析

蠕变模型的建立对于研究与预测组合柱在长期荷载作用下的变形具有重要的作用.以一维线性黏弹性理论为基础,将普通蠕变分为3部分：弹性变形、黏弹性变形与黏性变形[21].其中,弹性变形为可恢复的变形,黏弹性变形为与时间相关且可恢复的变形,而黏性变形为永久的不可恢复变形.如图7所示,常用Maxwell模型、Kelvin模型与Burger模型描述木质材料蠕变变形,对应的蠕变表达式分别为：

图7 蠕变力学模型Fig.7 Mechanical models of creep

(1)

(2)

(3)

式中：uM、uK、uB分别为基于Maxwell模型、Kelvin模型与Burger模型的蠕变变形,mm;P0为长期荷载施加值,kN;ke1与ke2为Maxwell模型与Kelvin模型的弹性系数,MPa;γv1与γv2为Maxwell模型与Kelvin模型的阻尼系数,MPa·d.

以组合柱试件ZC-N2-2为例,试用Maxwell模型与Kelvin模型对长期荷载作用下组合柱的蠕变进行分析,并绘制考虑初始变形的蠕变曲线,如图8所示.由图8可见：Maxwell模型曲线为1条直线,拟合曲线随着时间的推移,逐渐偏离试验曲线且不具备收敛性;Kelvin模型拟合曲线起点为坐标原点,在长期荷载加载初期与试验曲线偏差较大,但加载后期对试件黏弹性变形拟合效果较好且具有收敛性.

图8 试件ZC-N2-2的蠕变试验曲线与拟合曲线Fig.8 Experimental and fitted creep-time curves of specimen ZC-N2-2

从Maxwell模型表达式分析,该模型具备模拟弹性变形与黏性变形的特性;从试件ZC-N2-2拟合分析结果可知,Kelvin模型能够较好地模拟黏弹性变形.由此,将两者串联形成的Burger模型,应能良好地模拟普通蠕变的主要特征.各试件对Burger模型的参数拟合结果如表5所示,其相关系数R2均在0.95以上,可见Burger模型可以较为准确地描述组合柱的蠕变行为.拟合蠕变曲线如图9所示.

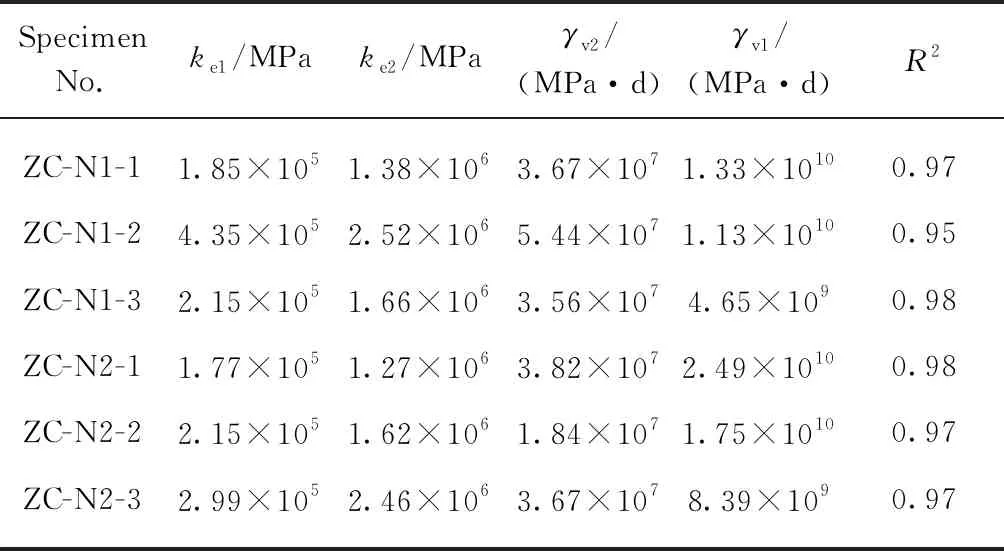
表5 Burger模型的参数拟合

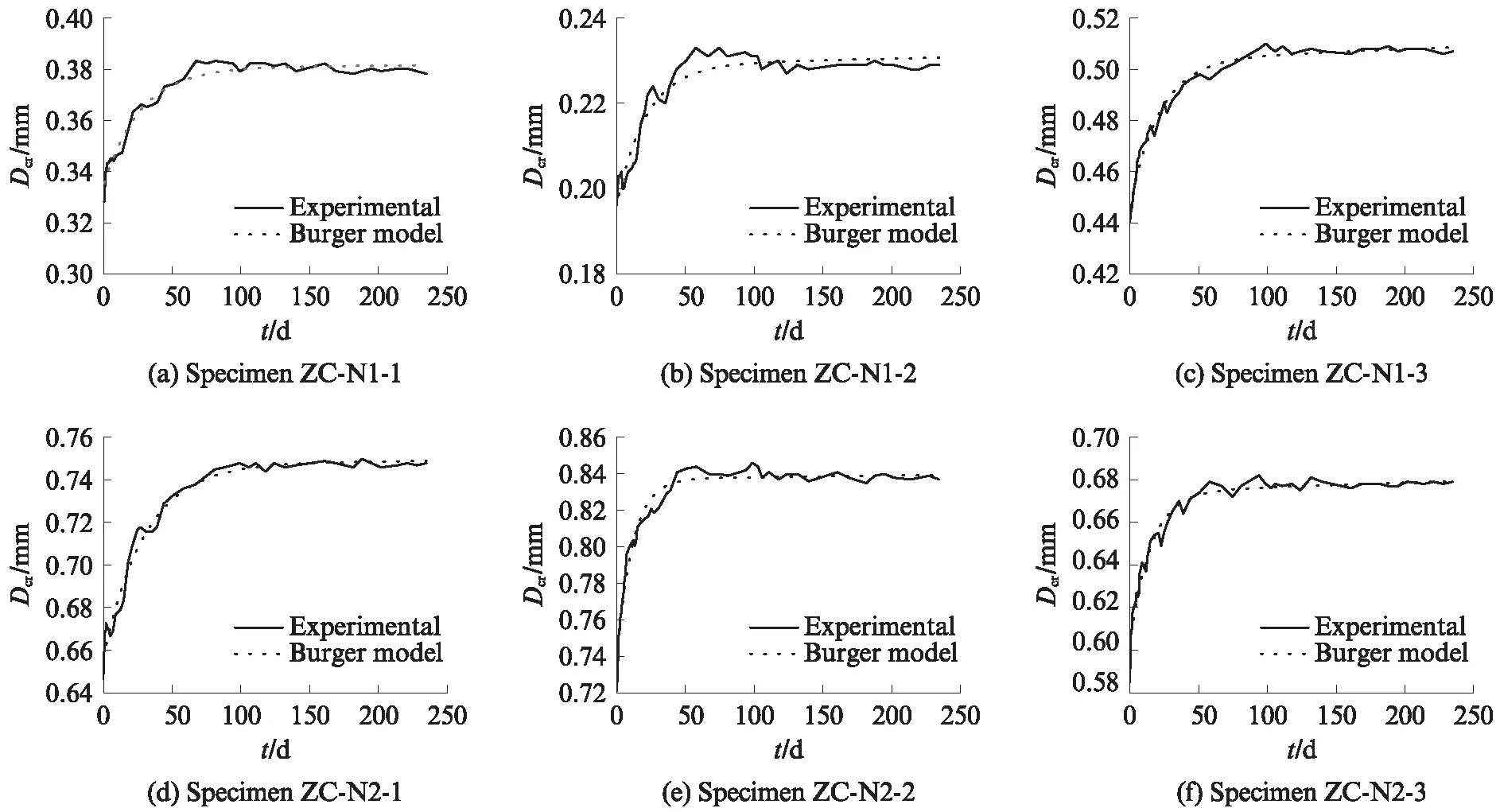
图9 组合柱蠕变曲线与Burger模型曲线对比Fig.9 Comparison of creep-time curves in test and in Burger model

以Burger模型为基础,可以计算组合柱试件在任意时间节点的蠕变总量及三组分变形分量.选取施加长期荷载后的第30、60、90、120、150、235d作为计算时间节点,分析蠕变总量中的弹性变形、黏弹性变形及黏性变形,以试件ZC-N1-1为例,计算结果如表6所示.由表6可见：长期荷载施加完毕后立刻产生弹性变形,其数值在整个持荷期间保持恒定,占蠕变总量的85%～88%;黏弹性变形在加载初期发展速度较快,在90d左右已完成黏弹性变形总量的95%;黏性变形数值较小,随持荷时长匀速发展,在蠕变总量中所占比例较低.长期荷载加载完毕后,蠕变总量的提高主要源于黏弹性变形的发展,考虑到黏性变形所占比例较低,故蠕变总量在90d左右已基本稳定,达到最终蠕变的95%以上.

表6 试件ZC-N1-1蠕变变形各组分计算

选取含钢率相同的3组试件(ZC-N1-1与ZC-N2-1,ZC-N1-2与ZC-N2-2,ZC-N1-3与ZC-N2-3)分析其蠕变特征,可知随着加载水平的提高,弹性变形与黏弹性变形显著发展,而黏性变形变化较小,在蠕变总量中所占比例随加载水平的提高而降低.选取同一加载水平的2组试件(ZC-N1-1～ZC-N1-3,ZC-N2-1～ZC-N2-3)分析其蠕变特征,黏性变形数值与含钢率呈正相关,黏性变形发展速率及其在蠕变总量中所占比例随含钢率的增大而提高.上述分析表明,加载水平是影响蠕变性能的重要因素,应在实际工程中严格控制.

3 二次加载试验结果与分析

3.1 试验结果

二次加载试验过程中,将组合柱所能承受的最大荷载定义为极限荷载试验值.长期加载试件的屈服荷载试验值、极限荷载试验值(Nu)及对应的屈服位移(Δy)、极限位移(Δu)如表7所示.

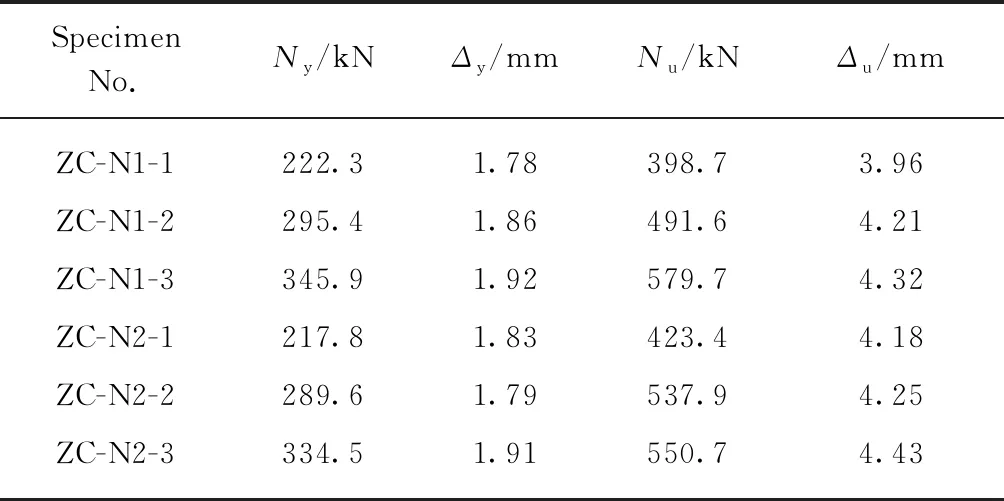
表7 二次加载试验结果

3.2 破坏形态

与一次加载试验相比,二次加载试验与其颇有相似之处,长期荷载作用未导致破坏模式发生显著变化.试件ZC-N1-1、ZC-N1-2、ZC-N2-1和ZC-N2-3的破坏特征较为相似,表现为试件翼缘处竹胶板沿竖直方向发生劈裂破坏,如图10(a)所示;试件ZC-N1-3与ZC-N2-2在轴压荷载作用下翼缘处竹胶板被压溃,随后薄壁型钢发生屈曲破坏,如图10(b)所示.经过长期加载试验,钢-竹界面黏结胶体固化水平提高,降低了潜在黏结界面初始缺陷带来的不利影响.与一次加载试验相比,钢-竹界面黏结更为可靠,未发生因胶合界面局部脱胶而导致的破坏.

图10 试件主要破坏形态Fig.10 Primary failure models of specimens

3.3 荷载-应变关系曲线

通过二次加载试验可以得到试件的荷载-纵向应变(N-ε)关系曲线,如图11所示.由图11可见：当轴向荷载小于0.55Nu时,试件处于线弹性工作阶段,未出现明显破坏征兆,偶有细微竹胶板开裂声,薄壁型钢与竹胶板的应变发展规律基本一致,两者表现出良好的组合效应;当轴向荷载超过0.55Nu后,曲线呈非线性发展趋势,组合柱进入弹塑性工作阶段,最终试件上端翼缘处竹胶板发生劈裂破坏,同时薄壁型钢发生局部鼓屈,导致试件丧失承载力.

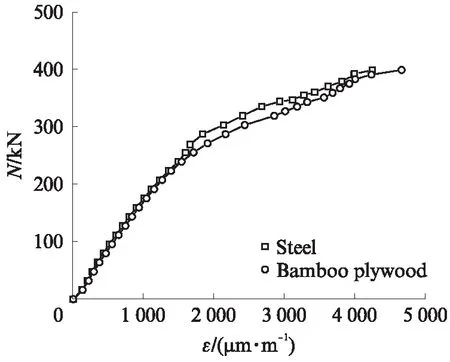
图11 二次加载试件ZC-N1-1荷载-应变关系曲线Fig.11 N-ε curves of specimen ZC-N1-1 in secondary static loading test

3.4 二次加载试验影响因素分析

试件极限承载力Nu、极限应变εu与加载水平ξ的关系如图12所示.由图12可见：随着加载水平的提高,含钢率相同试件极限承载力的变化幅度较小,介于-5.00%～9.42%之间;随着加载水平的提高,试件极限应变显著提高,增幅可达11.60%～25.44%;在长期荷载作用下,试件极限承载力所受影响较小,较大的蠕变总量使竹胶板及钢-竹胶合界面潜在初始缺陷得到了改善,当加载水平ξ由0.30增大至0.56时极限应变显著提升,有助于提高构件服役期间的工作应力.

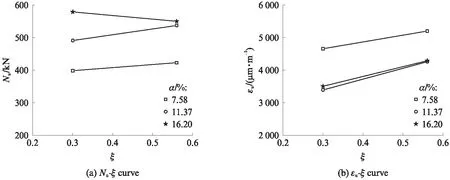
图12 极限承载力、极限应变与加载水平的关系曲线Fig.12 Curves of Nu-ξ and εu-ξ

相同加载水平试件的荷载-应变曲线如图13所示.由图13可见：试件的极限承载力随着含钢率的增大而提高,含钢率较大的试件进入弹塑性破坏阶段较晚,增大了弹性工作区间.以加载水平ξ=0.30的试验组为例,试件含钢率之比为1∶1.50∶2.14,屈服荷载之比为1∶1.33∶1.56,极限荷载之比为1∶1.23∶1.45.由此可见,含钢率与承载力呈正相关,对长期荷载作用后的组合柱的轴压性能影响显著.

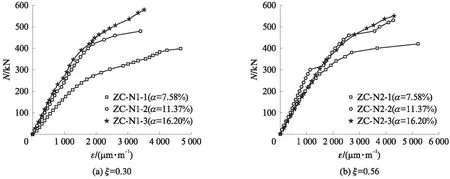
图13 相同加载水平试件荷载-应变关系曲线Fig.13 N-ε curves of specimens under same loading level

3.5 二次加载试验与一次加载试验对比分析

图14为一次加载试件与二次加载试件的荷载-应变关系曲线.由图14可见：二次加载试验试件的极限承载力受长期荷载作用的影响并不显著,平均降幅约5.09%;试件的极限应变明显提高,平均增幅达24.49%.

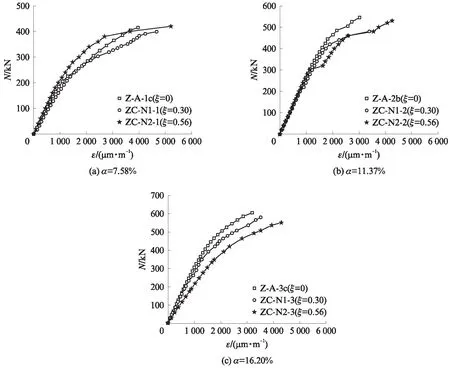
图14 一次加载试验与二次加载试验荷载-应变关系曲线对比Fig.14 Comparison of N-ε curves in static loading test and secondary static loading test

为了便于考察长期荷载作用对组合柱承载力和变形的影响规律,定义3个影响系数[22]：承载力影响系数SI=NuL/Nuo,其中NuL、Nuo分别为二次加载试验和一次加载试验构件的极限承载力;变形影响系数DI=εuL/εuo,其中εuL、εuo分别为二次加载试验和一次加载试验构件的极限应变;延性影响系数KI=μL/μo,其中μL、μo分别为二次加载试验和一次加载试验构件的延性系数,且延性系数为极限位移与屈服位移的比值.影响系数SI、DI、KI与含钢率、加载水平的关系如图15所示.由图15可见：一次加载与二次加载试验试件的极限承载力没有明显差异,且SI数值呈现出一定的跳跃性,表明试件的极限承载力受长期荷载作用的影响并不显著;DI数值位于1.101～1.314之间,可见二次加载试验试件的极限应变较一次加载试验有显著的提高,且DI数值随着含钢率的增加而减小,随着加载水平的增大而提高;试件的延性随含钢率的增大而显著提高,与加载水平正相关.

4 结论

(1)加载初期,组合柱的蠕变速率较快,当加载至30、60d时,组合柱的蠕变量分别占蠕变总量的75%和90%左右,在加载100d之后,蠕变曲线渐趋水平,组合柱的蠕变变形达到稳定阶段.

(2)长期荷载加载完毕后,蠕变变形的增长主要源于黏弹性变形的发展,4因素Burger模型可以较准确地模拟组合柱的蠕变行为,拟合曲线和试验曲线的相关系数R2均在0.95以上.

(3)随着加载水平的提高,蠕变弹性变形、黏弹性变形及蠕变总量均显著增大,而蠕变黏性变形却基本保持不变,黏性变形占蠕变总量的比例随加载水平的提高而降低,黏性变形发展速率及其在蠕变总量中所占比值随含钢率的增大而提高.

(4)长期荷载作用后钢-竹界面黏结可靠性提高,未发生因黏结界面脱胶而导致的破坏,二次加载试验主要破坏模式包括翼缘竹胶板竖向劈裂破坏、翼缘竹胶板压溃后薄壁型钢局部屈曲破坏.

(5)长期荷载作用对组合柱极限承载力的影响并不明显,但组合柱的极限应变与延性显著提高,有利于提高组合柱工作应力,随着含钢率的提高,组合柱承载力与延性显著提升.