装配式高层钢框架-自复位混凝土筒体组合结构振动台试验模型设计

周 颖 宋朝阳

（同济大学土木工程防灾国家重点实验室，上海200092）

0 引 言

经过多次强烈地震灾害的检验，现如今我国传统结构的抗震设计已基本能够满足“小震不坏、中震可修、大震不倒”的三水准抗震设防目标。然而，随着社会经济的快速增长以及结构抗震技术理论的发展，人们对结构的抗震性能提出了更高的要求。为克服传统结构震后损伤严重、修复周期长甚至难以修复的缺点，地震损伤小、震后可恢复的可恢复功能防震结构体系逐渐成为工程师们关注的重点［1］。

自复位结构体系是可恢复功能防震结构体系的一种，主要包含自复位框架结构、自复位剪力墙结构、自复位支撑-框架结构等，相比传统结构具有变形能力大、残余变形小的优点［2-3］。自复位筒体结构建立于自复位剪力墙结构的理论基础上，筒体由多面自复位墙组成，各墙体具有独立摇摆的能力，其可开合接缝通过预应力连接在一起，将构件的材料变形转变为结构接缝处的几何变形，大大降低了构件自身的损伤。现如今，国内外对自复位墙相关的研究多停留在单片剪力墙或双向非耦合剪力墙结构，因此有必要构建三维自复位筒体结构并进行整体结构的动力试验研究。

为研究新型装配式自复位筒体结构的整体抗震性能及其特殊细部构造的有效性，同济大学土木工程防灾国家重点实验室开展了装配式高层钢框架-自复位混凝土筒体组合结构的模拟地震振动台试验。本文对该振动台试验模型设计进行了详细的介绍，主要围绕结构体系的作用机理、试验模型的设计计算流程和该结构特殊的细部构造等进行了阐述，为今后类似的装配式高层自复位筒体结构的设计和试验提供参考。

1 试验模型概况

试验采用同济大学土木工程防灾国家重点实验室的4.0 m×4.0 m模拟地震振动台。试验模型为1∶6比例缩尺的装配式高层钢框架-自复位混凝土筒体组合结构。结构总高为5 m，层高0.5 m，共10层。结构平面双轴对称，平面尺寸为3.5 m×2.9 m。试验模型的结构示意如图1所示。

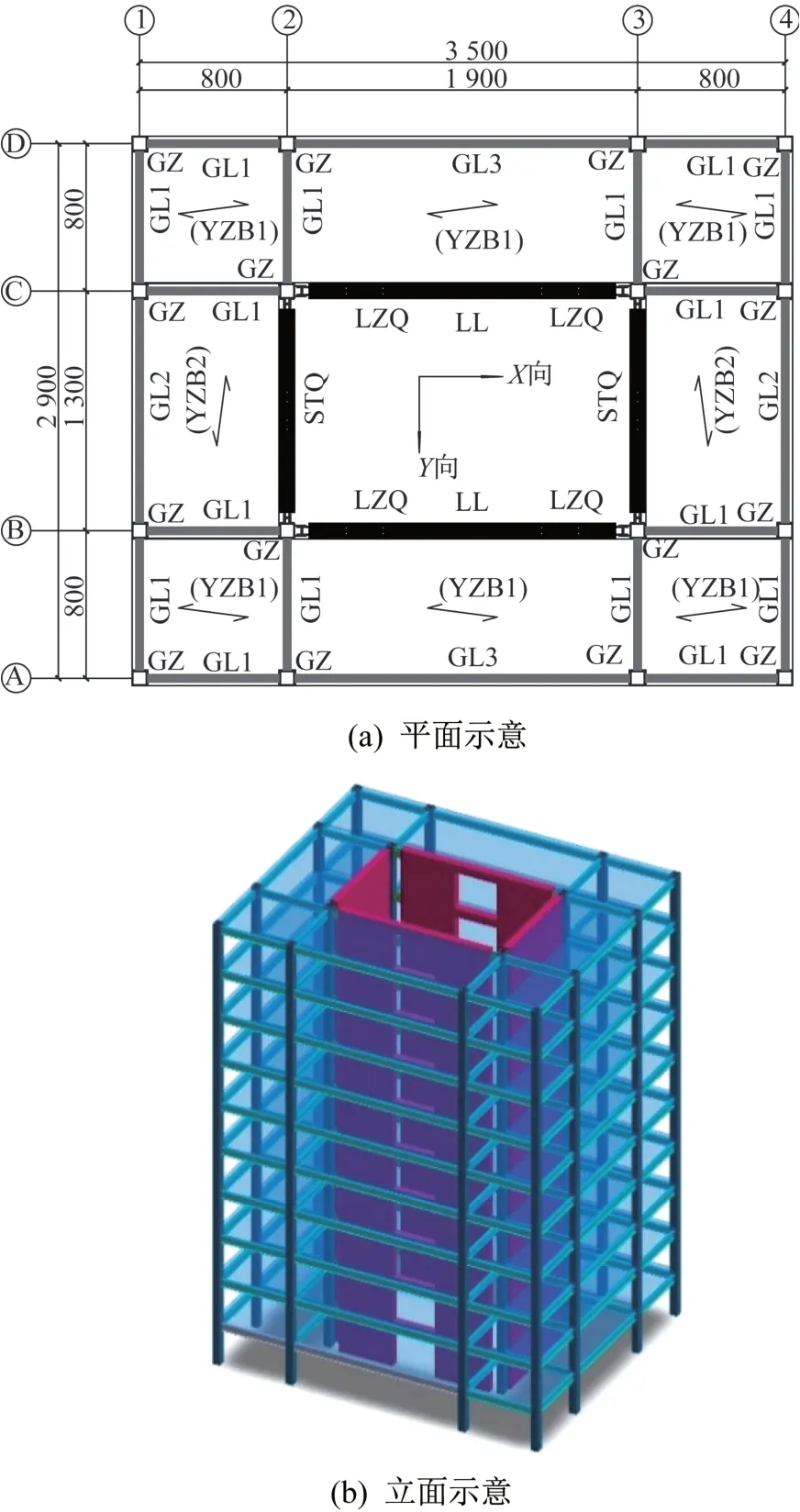
图1 试验模型结构示意图（单位：mm）Fig.1 Schematic diagram of the model building（Units：mm）

结构主体由承担竖向荷载的外围框架和抵抗水平作用的内部自复位筒组成。框架柱为80 mm×80 mm×4 mm×4 mm的箱形钢柱，框架梁为80 mm×40 mm×3 mm×3 mm的H型钢梁，柱脚及梁柱节点均采用铰接连接。楼板采用30 mm厚度的压型钢板组合楼板。内部自复位筒体由四片自复位混凝土墙组成，沿模型X向为1 660 mm×80 mm的自复位联肢墙（包含长度460 mm的自复位连梁），沿模型Y向为1 100 mm×80 mm的自复位整体墙。自复位墙端部通过预埋的滑槽节点板与钢柱相连，以组成完整的筒体，可保证外围框架在水平方向上与内部筒体协同运动，但不阻碍筒体墙竖直方向上的自由抬升与接缝的开合。

该试验模型设计场地的抗震设防烈度为8度（0.20 g），设计地震分组为第二组，场地类别为Ⅱ类，场地特征周期为0.4 s。

2 模型设计过程

2.1 相似关系

综合考虑模拟地震振动台的性能参数、实验室的施工条件及吊装能力等因素，首先，确定试验模型的几何相似常数SL=1/6；其次，考虑到振动台噪声、台面承载力和振动台性能参数等因素，选择加速度相似常数Sa=1.50；最后，依据实验室可以实现的混凝土强度确定弹性模量相似常数SE=0.25。试验模型的相似关系见表1。

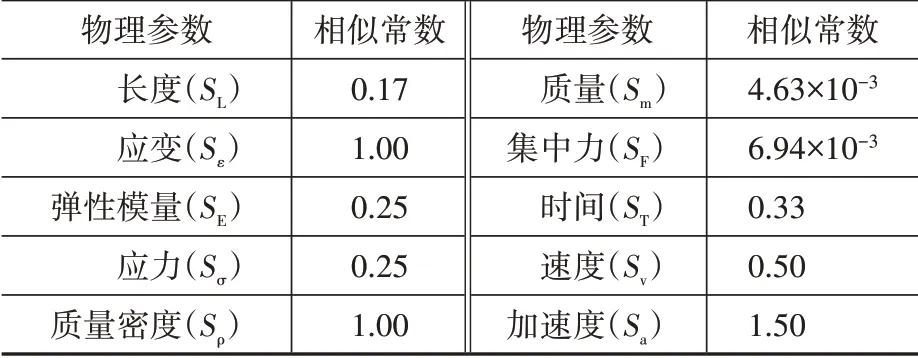
表1 试验模型相似关系Table 1 Similitude relation of the model building

2.2 模型材料

缩尺模型材料的弹性模量应尽可能小、比重应尽可能大，同时应力-应变关系应尽可能与实际的原型材料相似。基于以上考虑，采用C15等级的细石混凝土模拟实际的高强度混凝土，以镀锌铁丝模拟普通钢筋。试验用钢材、预应力钢筋及耗能钢筋分别采用Q235B标准钢材、抗拉强度1470 MPa的预应力光圆钢丝以及Q235B圆钢，通过对模型附加质量进行适当的调整以满足相似关系要求。

2.3 构件设计

相比传统的基于力的抗震设计方法，直接基于位移的抗震设计方法更适用于自复位结构体系，并可以有效降低结构成本［4］。本文参考周颖等［5］提出的四水准下基于位移的抗震设计理论，直接对试验缩尺模型进行性能设计，具体过程如下：

（1）确定设计位移目标及有效阻尼比。直接针对第四水准进行结构的极限状态设计，设计目标位移角取为2%。有效阻尼比为结构弹性阻尼比和塑性滞回阻尼比之和，其中弹性阻尼比取为3%。考虑到现如今缺少切实可行、方便直接的自复位墙结构塑性滞回阻尼比估算方法，本文依据自复位墙结构的旗帜形滞回曲线特点，提出以下方法近似计算结构X向和Y向的塑性滞回阻尼比。参考Priestley［6］的推荐公式，自复位墙结构的塑性滞回阻尼比按照滞回圈面积计算，公式如下：

式中：ξhyst为塑性滞回阻尼比；η为滞回响应和非线性时程响应的塑性耗能修正系数，对于塑性耗能能力较低的自复位墙结构可保守取值为1.0；β为旗帜形滞回曲线的形状系数，与结构耗能能力密切相关，按照新西兰规范［7］的建议应不大于0.93；r为屈服后刚度比，建议的取值范围为0.003～0.05；μ为延性比，μ=θd/θy。

屈服状态时墙底受压区混凝土长度一般在0.20lw～0.30lw之间，可近似取为0.25lw。因此，延性比可近似按公式（2）计算，计算得结构X向和Y向的延性比分别为13和16。

式中：θd为设计目标位移角；θy为屈服状态下的墙底转角；lw为墙截面长度；le为耗能钢筋的无黏结长度；εey为耗能钢筋的屈服应变。

自复位墙极限位移和屈服位移下的基底弯矩比值一般在1.2～1.4［8］。考虑到一般墙截面长度越大，屈服后强度增长越快，结构X向和Y向极限弯矩和屈服弯矩的比值分别取1.2和1.4，按式（3）计算X向和Y向的屈服后刚度比分别为0.017和0.027 。

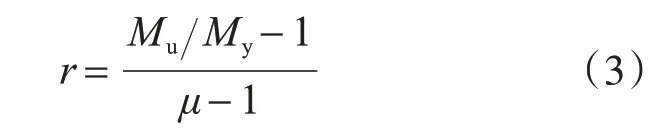
式中：Mu为设计目标位移下结构的基底弯矩；My为结构屈服位移下的基底弯矩。

旗帜形滞回曲线的形状系数作为截面设计的指导参数需要预先选取，鉴于墙截面长度更大的自复位整体墙更有利于发挥墙底耗能钢筋的塑性耗能能力，X向和Y向分别取0.45和0.55。因此，可按式（1）计算得结构X向和Y向的塑性滞回阻尼比分别为10.8%和11.4%。

（2）计算等效单自由度体系参数。直接基于位移的抗震设计方法将多自由度体系等效成单自由度体系，主要考虑结构第一振型的影响，计算公式如下：

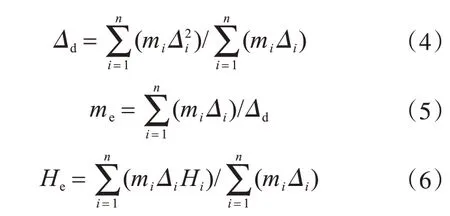
式中：Δd为有效设计位移；me为有效质量；He为有效高度。

试验模型质量根据原型结构的质量分布按相似关系确定。各层质量取楼层上下各一半层高范围内的结构总质量，重力荷载代表值取1.0恒载+0.5活载。楼层位移按线性分布计算得到，结构楼层参数见表2。计算得Δd=68.52 mm，me=11.28 t，He=3.426 m。

表2 结构楼层参数Table 2 Geometric information of structural stories

（3）建立等效弹性位移谱。结构位移谱采用欧洲规范［9］建议的等效弹性位移谱，见式（7）、式（8）。该公式适用范围较广，当周期较短时（T≤3 s），对于较大的阻尼比（ξ≤0.25）也有着很好的精度。

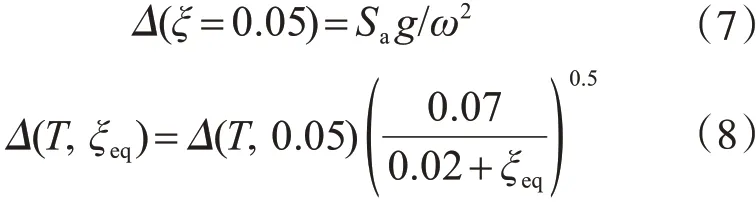
式中，ξeq为结构有效阻尼比，为结构弹性阻尼比和塑性滞回阻尼比之和。

8度抗震设防烈度第四水准的水平地震影响系数最大值为1.35。根据抗震规范［10］建立设计场地的规范反应谱，根据式（7）将规范反应谱转换为弹性位移谱，并依据相似关系和有效阻尼比将弹性位移谱按式（8）转换为试验缩尺模型的等效弹性位移谱，如图2所示。由等效弹性位移谱可得，结构X向和Y向的有效周期Teff分别为0.972 s与0.983s。

图2 结构等效弹性位移谱Fig.2 Equivalent elastic displacement response spectra

（4）确定结构地震作用力。根据式（9）、式（10）计算得结构X向、Y向的地震合力分别为32.27 kN与31.58 kN，地震作用引起的基底倾覆弯矩分别为110.5 kN·m与108.2 kN·m。

式中：V为基底剪力；Fi为第i层的楼层地震力。

鉴于外围框架仅作为结构的承重体系，结构的水平地震作用全部由自复位筒体承担。设计时可忽略筒体墙在平面外方向的抗侧能力，认为地震力完全由该方向上的自复位筒体墙承担。此外，由于此时结构的侧向位移已经较大，应计入P-Δ效应。由于直接基于位移的抗震设计预先确定了结构的侧向位移模式，故结构的P-Δ效应可以直接求解。最终，结构X向自复位联肢墙的底部剪力为17.62 kN，底部倾覆弯矩为59.00 kN·m；Y向自复位整体墙的底部剪力为17.26 kN，底部倾覆弯矩为57.76 kN·m。

（5）检验结构位移模式的准确性。建立各筒体墙的弹性模型，根据求得的地震力计算墙身变形的大小。计算得X向、Y向墙身变形引起的位移角仅为0.12%与0.08%，仅占设计位移角的6%和4%，说明线性位移分布假定符合该结构的设计要求。

（6）墙截面配筋与构造设计。自复位筒体墙截面的承载力设计可参考Perez等［11］提出的计算方法，筒体墙的设计参数如表3所示。图3为Y向整体墙底部截面的设计原理示意，其他截面的设计原理类似。自复位墙体的构造设计参考杨博雅等［8］提出的构造设计方法，本文试验缩尺模型的自复位筒体墙的构造措施均满足设计要求。

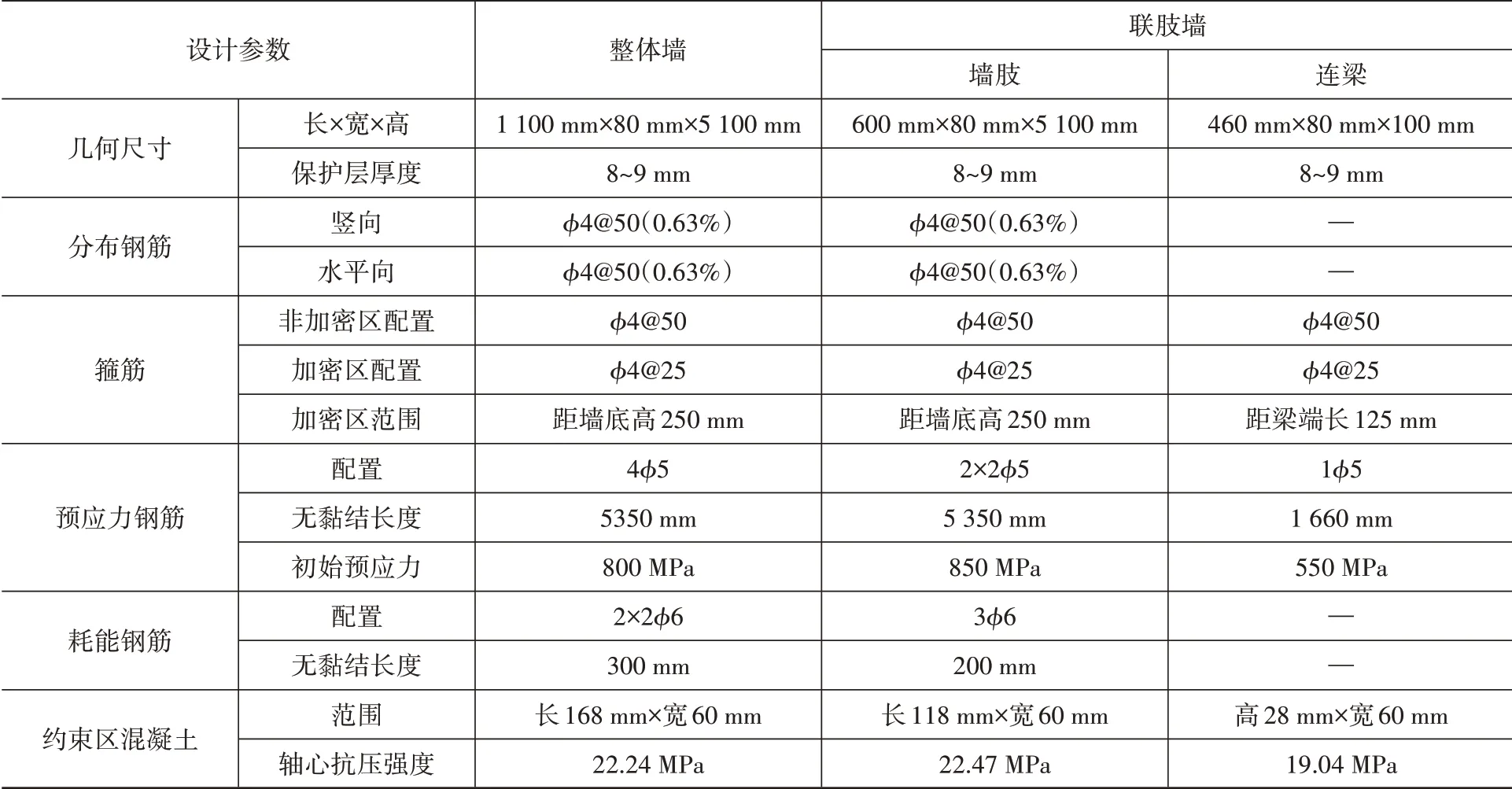
表3 自复位筒体墙设计参数Table 3 Design parameters of self-centering tube walls

图3 Y向自复位整体墙底部截面设计示意Fig.3 Designing diagram of base joint of self-centering integral wall in Y direction

（7）校验与迭代计算。初步设计完成后，采用OpenSees软件对所设计的筒体墙进行数值模拟，并进行低周往复加载分析（图4），以校验结构有效阻尼比。根据滞回曲线计算得结构X向和Y向的塑性滞回阻尼比分别为10.5%和11.5%，与步骤1中计算结果的误差仅为2.9%和0.9%，符合设计精度要求，无须重复迭代计算。可见，本文提出的自复位墙结构塑性滞回阻尼比的初步估算方法是可行的。

图4 自复位筒体墙基底剪力-顶点位移角滞回曲线Fig.4 Base shear-roof drift hysteretic curves of selfcentering tube walls

3 模型细部构造

3.1 可开合接缝

在筒体墙接缝的开合过程中，接触面之间（墙底与基础面之间、墙端与梁端之间）会发生较剧烈的碰撞。如果接缝处没有合适的过渡垫层，接触面上的混凝土会因冲击碰撞而破坏，从而导致接缝截面抗弯、剪承载力过早地下降。接缝处的过渡垫层应具有足够的强度与良好的韧性，可采用的垫层种类有很多，包括纤维砂浆垫层、钢板垫层、环氧树脂垫层等。已有的试验结果［12～14］表明，这几类垫层都具有很好的过渡、缓冲作用。其中，纤维砂浆垫层性能优良、便于施工，并能提供较大的摩阻力，因此应用较广。但对于缩尺比例较大的模型，较小厚度的纤维砂浆垫层性能不稳定，厚度较大则会因剪应力而过早破坏。故本文的试验缩尺模型采用钢板垫层，墙底接缝和连梁端部接缝处均铺设了5 mm厚度的钢板（图5）。相比砂浆层，钢板与混凝土之间的摩擦系数较小，故对钢板表面做喷砂处理，以提高接触面的摩擦性能。

图5 筒体墙可开合摇摆接缝Fig.5 Rocking joint of self-centering tube wall

此外，考虑到可开合接缝处抗剪切滑移能力的重要性，在各接缝处额外添加了抗剪装置（抗剪螺栓、止滑角钢等），以防接触面摩擦失效从而导致结构的意外倒塌。抗剪装置与摇摆构件之间存在一定的间隙，仅在接缝处摩擦失效、发生剪切滑移时发挥作用，不会影响结构预期的性能。

3.2 墙段拼接

一面完整的自复位筒体墙（肢）由两个或多个预制墙段拼接而成。在墙段拼接处需采取可靠且合适的连接方式，既能使装配成型后的筒体墙作为一个整体进行运动，又能使墙段连接接缝处具有一定的可开合能力，从而降低地震作用下墙片自身的损伤。为此，本文试验采用了纤维砂浆坐浆、后浇锚固端部无黏结抗弯钢筋的湿连接方式进行墙段拼接（图6）。纤维砂浆为M20强度等级的掺聚乙烯醇纤维（体积率0.1%）水泥砂浆，后浇锚固区域则采用了高强度无收缩灌浆料。

图6 自复位墙段拼接接缝Fig.6 Upper joint of self-centering tube wall

3.3 滑槽连接节点

由于自复位墙在地震作用下作刚性摇摆，摇摆过程中的墙体抬升会对相邻的结构构件造成损坏。采用传统的连接构造方式会导致墙体摇摆时与楼板发生碰撞，或连梁因伸长效应与楼板产生挤压，造成楼板的局部损坏，影响结构的低损伤特性，并会在一定程度上阻碍自复位墙的摇摆性能。现有的方法是选择削弱墙体与相邻结构构件的连接，从而减轻楼板的损伤，但这种方法不能从根本上避免这一问题。

因此，本文为防止外围铰接框架阻碍自复位筒体的摇摆性能，在筒体墙端部预埋竖向滑槽节点板，以保证柱体不阻碍墙体的自由抬升；而在柱端焊接横向滑槽节点板，使得筒体墙与钢柱之间仅传递水平接触拉力，以防平面内刚度较大的楼板阻碍连梁端部接缝的开合。该连接构造使得各筒体墙具有独立摇摆的能力，并达到结构承重体系与抗侧体系完全分离的目的，是实现自复位筒体性能至关重要的构造措施。筒体墙和钢柱之间滑槽连接节点的构造如图7所示。

图7 墙柱间滑槽连接节点Fig.7 Channel joint between self-centering tube wall and steel column

相比传统的节点板连接，滑槽节点要求节点板具有足够的厚度，以保证：①竖向滑槽平面不会因连接螺杆的滑动接触而发生塑性承压破坏；②横向滑槽端部不会因连接螺杆的碰撞而断裂。因此，本文的试验缩尺模型人为地加厚了滑槽节点板的厚度，各节点板的厚度均为5 mm。

4 结 论

本文介绍了新型装配式自复位筒体结构体系及该结构振动台试验缩尺模型的设计过程。对结构体系、试验模型的设计过程及特殊的细部构造进行了详细的介绍，涉及了振动台试验中诸多的关键问题——相似关系、材料、构件、细部构造等，以期为今后类似的装配式高层自复位筒体结构的设计和试验提供参考。