一种高效的混凝土框架结构优化设计方法

楼善治 张海静

（上海大学土木工程系，上海200072）

0 引 言

随着计算机技术的进步，遗传算法发展十分迅速，有大量关于遗传算法的专著及研究文献出现。在框架结构设计优化领域，也有越来越多的学者运用遗传算法解决工程问题。

S.Rajeev［1］把离散变量的概念用于基于标准遗传算法的钢筋混凝土框架优化设计研究。Hongjin Kim［3］利用实数编码遗传算法对钢筋混凝土框架优化设计，克服了二进制编码个体编码冗长的缺陷。陈雨生［4］采用平面框架有限元程序和MATLAB遗传算法工具箱结合开发了实用的优化系统程序。但在优化程序中仅考虑了构件的强度约束，结构的整体位移约束则通过手动调整变量值来实现。张琦［5］以结构造价最小为目标函数，通过可靠度理论，对各类约束进行处理，优化结果与实际工程更贴近。但其在约束处理过程中仅考虑了构件的强度和刚度约束，没有考虑结构的整体位移约束。

遗传算法解决工程时的一个较大缺陷是在搜索过程中需要不断对个体进行结构分析，从而导致计算效率低下。实际工程通常结构体型较大，优化时设计变量个数较多，遗传算法的种群规模也需相应地取较大值，若对每一个个体都进行结构分析，会造成优化设计的时间成本过高的问题。本文采用构件内力静定化假设，在每一轮优化的过程中冻结构件内力，避免了在优化过程中进行大量的结构分析，极大地提高了计算效率。

学者们在将遗传算法运用于框架结构优化设计的领域上取得了一定的成果。但在上述列举的文献中，均未在优化程序中同时考虑构件约束和结构整体位移约束。本文将优化过程分为两部分：第一部分采用遗传算法对构件尺寸和混凝土强度等级进行优化设计，通过惩罚函数处理构件约束；第二部分采用准则法对不满足结构位移约束的最佳个体进行位移调整。这样在确保构件满足约束的同时，又能使结构整体满足位移约束。

现有的工程问题遗传算法优化设计研究中，很多学者采用的还是标准的交叉、变异、选择算子，而传统的遗传算法存在着局部寻优能力差、迭代过程缓慢、随机性大、易出现振荡和早熟收敛等缺点［6］。结构设计优化问题是一种多变量、多约束的复杂问题。为了得到更好的优化效果，本文对遗传算法进行改进，通过自适应的操作算子，在保证优化效果的同时，可以达到加速种群进化收敛的目的，节省了时间成本。

1 框架结构优化模型

1.1 优化变量设计

在材料单价确定的情况下，以造价为目标函数的优化问题中，框架结构的优化变量应为梁柱的b，h，纵向配筋值As和箍筋值Asv。当内力被冻结，纵向配筋值和箍筋值都可以通过尺寸参数和内力由规范［12-13］公式求得，也就是说纵向配筋值As和箍筋值Asv是关于构件b和h的函数［7］。因此，最终的优化设计变量仅仅是梁柱的截面尺寸b和h。实际工程中为了便于施工，同层柱的混凝土等级一般相同，故本文将每层柱的混凝土等级作为变量。梁的混凝土等级采用C30不变。

1.2 目标函数

本文以框架结构的经济效益为研究目的，因此采用框架主体部分的造价为目标函数。其中包括梁、柱混凝土，受力纵筋、箍筋以及模板。

1）单根梁造价

单根梁造价为

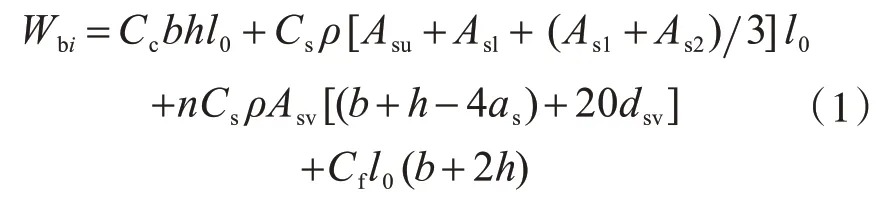
式中：b，h分别为截面宽度和高度；Cc为混凝土单位体积价格；Cs为钢筋的单位重量价格；受力筋和箍筋的单价统一取用Cs；ρ为钢筋的密度；Asu为上部架立筋截面面积之和；Asl为底部纵筋截面面积之和；As1，As2为梁端负弯起钢筋截面面积；Cf为模板单位面积价格；l0为构件长度；n为整根杆件的箍筋根数；Asv为单肢箍筋截面面积；as为保护层厚度。

梁的配筋立面图见图1，配筋剖面图见图2。

图1 梁配筋立面图Fig.1 Elevation of beam steel bar

图2 梁配筋剖面图Fig.2 Profile of beam steel bar

2）单根柱造价

单根柱造价为

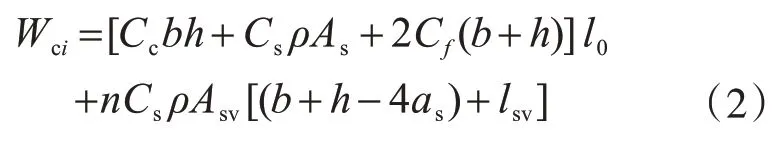
式中：As为纵筋面积之和；lsv为柱内部箍筋长度。

柱的立面图见图3，剖面图见图4。

图3 柱配筋立面图Fig.3 Elevation of column steel bar

图4 柱配筋剖面图Fig.4 Profile column steel bar

（3）钢筋混凝土框架结构的总造价为

式中，nc，nb分别为梁总数和柱总数。

1.3 约束条件

1.3.1 强度约束

1）梁

2）柱

（1）大偏心情况

（2）小偏压情况（x>x）

式中：

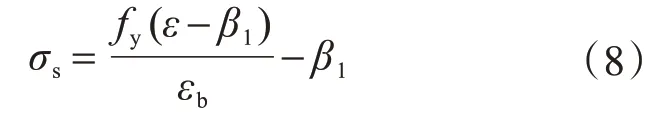
除满足式（7）以外，同时还需满足式（6）的第二式。

另外，在各种情况下还需满足斜截面承载力要求及轴压比限制要求：

式中，αac为轴压比限值。

框架结构抗震等级为一级、二级、三级、四级时分别取0.65，0.75，0.85，0.90。

1.3.2 构造约束

构造约束参照《混凝土结构设计规范》《建筑抗震设计规范》中的各项条文，如梁截面高宽比小于或等于4；构件截面最大及最小配筋率、配箍率；构件中钢筋最大及最小间距、箍筋肢数等。

1.3.3 位移约束

每层最大弹性层间位移角

式中：Δi为第i层的层间相对位移；h i为第i层的层高。

2 自适应遗传算法及优化流程

2.1 自适应遗传算法

遗传算法是借鉴了进化生物学中的一些现象而发展起来的一种启发式算法，这些现象包括遗传、突变、自然选择以及杂交等。传统遗传算法是仅使用选择算子、交叉算子和变异算子的最基本的遗传算法，其控制参数是事先确定且在遗传进化过程中保持不变的。如何最优给定有关控制参数，以便使遗传算法的性能最优，本身就是一个极其复杂的优化问题，要从理论上严格解决这一问题还很困难。自适应遗传算法通过对遗传参数的自适应调整，大大提高了遗传算法的收敛精度，加快了收敛速度［7］。

2.1.1 适应度函数

适应度是遗传算法中评判个体优劣的标准。适应度函数值越大的个体越接近最优解，能遗传到下一代的概率也越大。反之则概率越小。选取合适的适应度函数可以保证优秀个体能够有机会使优良特性得以遗传。本文采用的适应度函数为

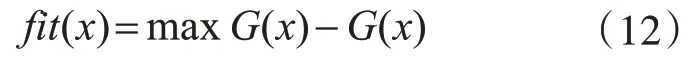
式中，G(x)是自适应惩罚函数，在2.1.3节会详细介绍。

2.1.2 选择、交叉、变异算子

1）自适应交叉算子

交叉概率和变异概率的取值对遗传算法的性能有很大的影响。交叉概率Pc值过大，新个体将快速出现，种群多样性更强，但容易破坏优秀个体的基因，造成优秀个体流失。Pc值过小，容易陷入局部最优解。传统遗传算法中Pc的取值往往需要多次试算来决定。为了克服上述困难，本文采用动态的自适应交叉算子，根据待交叉的两个个体的适应值来计算交叉概率，提高搜索速度的同时也保护优秀个体不受破坏［8］。自适应交叉概率的计算公式为

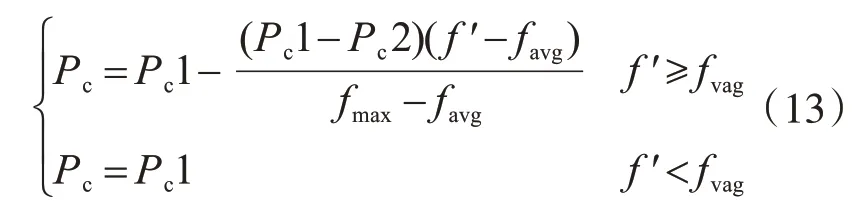
式中：favg为当前种群的平均适应值；fmax为当前种群中的最佳适应值；f′为待交叉的两个个体中适应度更高者的适应值。Pc1，Pc2为相关常数，可取Pc1=0.9，Pc2=0.6。

当待交叉的两个个体中适应值较大者的适应值不小于平均适应值时，调整减小交叉概率Pc；当待交叉的两个个体的适应值均小于平均适应值时，交叉概率Pc等于原先设定的初始交叉概率Pc1。

2）自适应变异算子

变异概率Pm过大会造成盲目搜索，Pm过小则难以产生新个体，种群多样性差。本文同样采用动态的自适应交叉算子，自适应变异概率的计算公式为

式中：f为待变异个体的适应值；Pm1，Pm2为相关常数，可取Pm1=0.1，Pm2=0.01。当待变异个体的适应值较大者的适应值不小于平均适应值时，按式（14）调整减小变异概率Pm；当待变异个体的适应值均小于平均适应值时，Pm等于原先设定的初始变异概率Pm1。

3）选择算子

本文根据选用适应度比例法进行选择。适应度比例法，又称轮盘赌选择法，是将个体的相对适应度作为该个体被选择的概率，某个体的相对适应度越高，它被选择的概率就越大。

2.1.3 约束处理

本文采用惩罚函数处理约束问题。惩罚函数是将约束条件的违反度作为惩罚项加到目标函数中，从而构造出带参数的增广目标函数。个体违反约束的程度越大，其对应的惩罚项的值和增广目标函数值越大，个体适应度值越小，从而达到使违反约束程度大的个体遗传到下一代的概率减小的“惩罚”目的。这种约束处理的思想是把一系列的约束优化问题转化成无约束的优化问题求解。

在约束条件下求函数最小值的数学表达式为

式中：f（x）为目标函数；Pm1和Pm1分别为不等式约束条件和等式约束条件；x∊Ω⊆S,S⊆Rn是搜索空间，Ω是可行域，即满足所有约束条件的空间。

惩罚函数方法把问题转化为min G(x)=f(x)+cφ(x)，其中，G（x）称为惩罚函数，c为惩罚因子，φ(x)为惩罚项。惩罚项个体到可行域的距离，个体x到第j个约束条件的距离可以表示为

传统的惩罚函数中，惩罚系数c的选取比较困难，c过大会降低对不可行域的搜索，因而失去由不可行解提供的一些有价值的的信息；c过小会导致约束条件被忽略。为了解决上述问题，蔡海鸾［10］提出了一种改进的自适应惩罚函数，利用当前群体总的可行解的比例来权衡目标函数和约束违反程度，实现对惩罚系数的动态调整。假设惩罚系数函数为

式中：ρ为可行解在种群中所占的比例；α是一个调整的参数，α>0，可取［0，10］之间的一个数。

综上可得自适应惩罚函数为

本文用自适应惩罚函数处理构件约束。层间位移角约束采用下文介绍的位移调整策略来实现。

2.2 准则法位移调整策略

在完成一次遗传算法后需要对获得的最优个体进行位移验算，如果不满足位移规范的要求，则从该个体出发，在其附近搜索满足位移约束的新个体，并令其替换为本轮整体优化的最优个体［11］。

本文结合传统设计时调整不满足层间位移角的思路，提出了一种基于准则法的简化调整策略，使得在遗传算法最优个体附近快速找到一个满足位移约束的个体。

传统结构设计实践中，当框架结构不满足位移约束时，有两种常见的调整思路：

（1）放大本层不满足位移要求方向的梁尺寸，一般只放大梁高尺寸；

（2）放大本层与不满足位移要求方向的同向柱边尺寸。

基于以上两种思路，本文设计了如图5所示的调整位移不满足约束的搜索策略：首先，把遗传算法计算出的最优个体分别按照上述（1），（2）思路进行模型调整；然后，比较两种思路调整后的个体适应值，取个体适应值最大的替换遗传算法的优化结果。

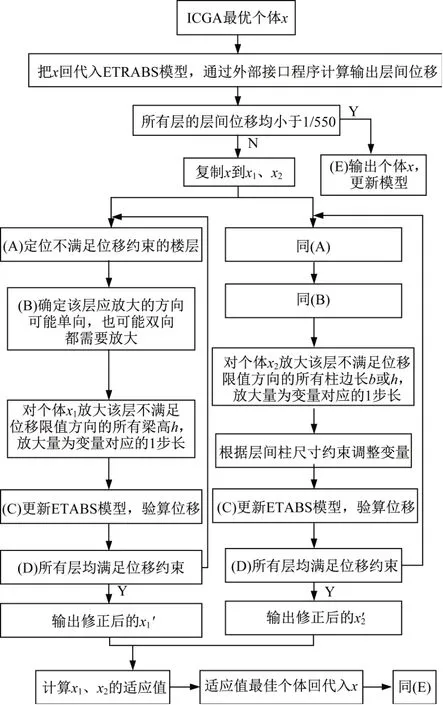
图5 位移不满足约束时的调整策略Fig.5 Adjustment strategy when the displacement does not meet the constraint

2.3 整体优化流程

本文采用分部优化思想来处理框架结构的尺寸和内力的非线性问题。整体优化分为两步执行，第一步冻结内力做结构尺寸的优化，第二步在第一步得到的新最优个体的基础上，更新模型内力，再次执行第一步的操作，反复这个过程直到造价满足收敛条件。

第一步优化又分两个级别。第一级为不考虑结构刚度对内力的影响，在梁柱构件约束和层间约束下执行遗传算法；第二级为在遗传算法优化得到的最佳个体后，将变量回代入有限元分析软件进行受力分析并输出层间位移，分析结果若不满足位移约束，则执行2.2节的位移调整策略不断更新ETABS模型，直到满足位移约束。整个优化过程的执行流程图见图6。

图6 钢筋混凝土框架结构整体优化流程Fig.6 Overall optimization process of reinforced concrete frame structure

3 框架结构优化实例

某8层钢筋混凝土框架结构，左右对称，结构层平面图见图7。初始模型各变量参数输入值见表2。结构设防烈度为7度（0.1g），地震分组为第一组。楼面恒荷载输入为2.5 kN/m2，活荷载输入为2.0 kN/m2，基本风压为0.55 kN/m2，地面粗糙程度为B类，场地类别为Ⅱ类。

图7 标准层平面图（单位：mm）Fig.7 Standard floor plan（Unit：mm）

图8 为该框架模型优化过程中的造价曲线。整体优化在第5次达到收敛精度要求，总耗时为18分33秒，框架优化后的造价收敛于428 833元，与原始模型相比减少了近25%的造价。表1为优化前后结构层间位移角，表2为优化前后各变量的值的对比。可见结构层间位移角均满足约束要求。

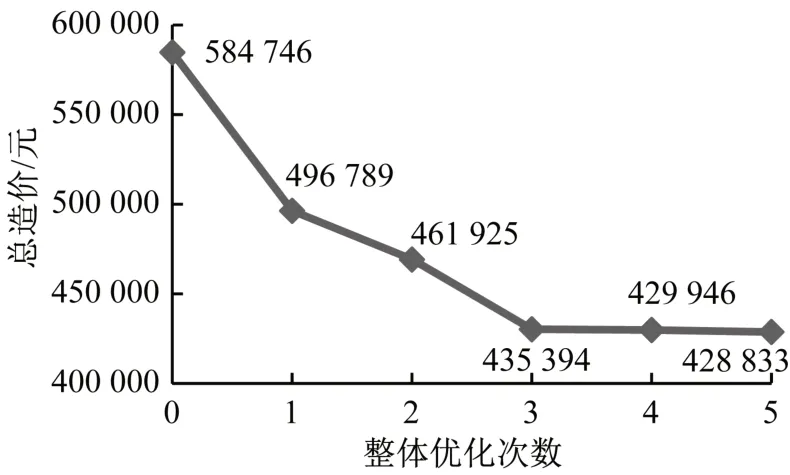
图8 结构整体优化造价下降曲线Fig.8 Cost decline curve of overall structural optimization

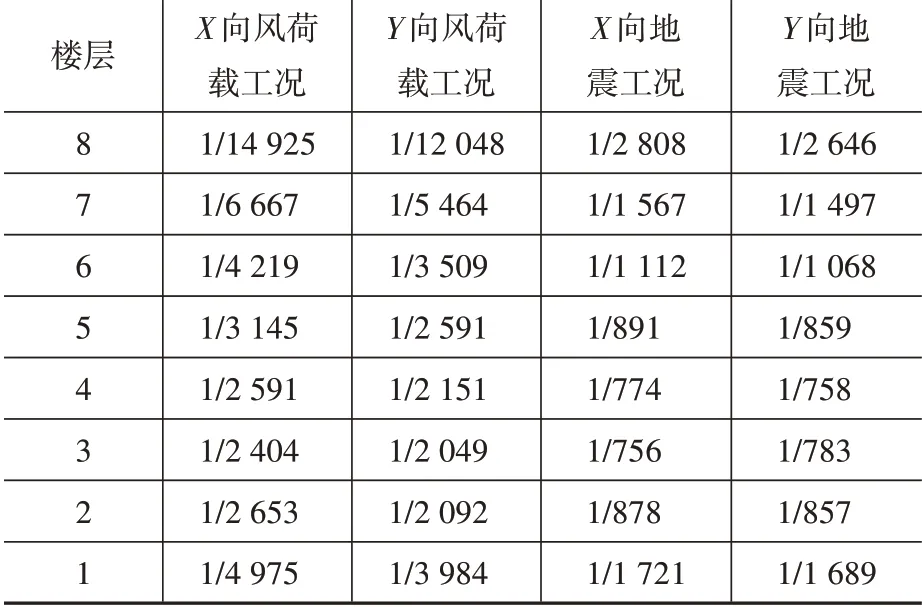
表1 框架结构优化后的层间位移角Table 1 Inter story displacement angle of frame structure after optimization

表2 框架结构优化前后数据对比Table 2 Data comparison of frame structure around optimization

4 结 论

本文采用自适应遗传算法，在内力静定化假设的前提下对钢筋混凝土框架结构进行了优化设计。内力静定化假设避免了在优化过程中进行大量的结构分析，极大地提高了计算效率。自适应遗传算法通过对遗传参数的自适应调整，大幅度提高了遗传算法的收敛精度，加快了收敛速度。通过算例实践，验证了本文设计的框架优化程序的可行性和实用性。在大大提高工作效率的同时，也能保证优化效果良好。