稳定拱肋对主拱肋力学行为影响的试验研究

申富林 宋小春 饶 瑞

（1.广州轨道交通系统装备安全与智能技术重点实验室，广州510006；2.广州大学-淡江大学工程结构灾害与控制联合研究中心，广州510006）

0 引 言

斜靠式拱结构具有外型美观、承载能力高、稳定性好等优点，在桥梁、屋盖等结构中应用逐渐增加。斜靠式拱结构形式较一般单拱结构复杂，其力学行为更加复杂多变，有必要进行深入研究，以满足实际应用的需要。

目前，关于拱桥结构力学行为的研究主要有理论研究和试验研究两种。理论研究包括：皮永林、刘爱荣及卢汉文等针对不同的拱结构线型、复杂边界条件以及荷载效应进行了单拱结构系列理论研究［1-6］，阐明了长细比、圆心角等对单拱结构稳定的影响机理；刘爱荣和申富林等针对斜靠式拱结构的承载能力展开了理论研究［8-10］，得出了横撑抗弯刚度、矢跨比、主拱肋边界条件等对斜靠式拱结构承载性能的影响规律。试验研究包括：赵思远等对钢管桁架拱、实腹式拱、工字形铝拱等单拱结构进行了稳定试验研究［7］；李康杰和陈林对组拼拱结构进行试验研究［11-12］，揭示了拱截面、横撑截面刚度以及长度等对组拼拱力学性能的影响；此外，赵露薇、沈烔伟、林天然等对钢管混凝土拱桥展开了动力、拱脚水化热及吊杆张拉力等方面的系列研究［13-15］。相对而言，关于斜靠式拱结构力学行为的研究涉及较少。

本文开展多点竖向荷载作用下斜靠式钢管圆弧拱结构的力学行为试验研究，着重考察稳定拱肋对主拱肋力学行为的影响，揭示稳定拱肋倾角对斜靠式拱结构主拱肋的力学行为影响规律，为斜靠式拱结构的设计与应用提供参考。

1 试验模型

1.1 试验模型设计

试验选用钢管和混凝土材料，主拱肋和稳定拱肋采用Q345B钢材，底座混凝土采用C35混凝土。此外，斜靠式拱结构试验模型中，主拱肋与稳定拱肋的线型均采用圆弧线型，其中主拱肋采用截面为Φ220×8的空心钢管，Φ表示为钢管外径，跨径为3 000 mm，矢跨比为1/4；稳定拱肋采用截面为Φ76×5的空心钢管，稳定拱肋倾角分别采用10°、20°、30°；横撑采用截面为Φ60×5的空心钢管，与主拱肋和稳定拱肋相互焊接，总数为5根，分别从跨中开始每隔500 mm布置1根，拱顶横撑长均设置为200 mm，斜靠式拱结构试验模型参数详见表1所示。此外，在加载装置中，底座采用长4 400 mm、宽1 600 mm、高400 mm的钢筋混凝土结构。斜靠式拱结构试验模型示意图如图1-图3所示，图1为斜靠式拱结构试验模型加载装置整体效果图；图2为斜靠式拱结构试验模型侧视图，其中，α表示稳定拱肋倾角，P表示竖向油压千斤顶施加的荷载；图3为斜靠式拱结构试验模型拱顶截面图，其中，t1、t2、t3分别表示主拱肋、稳定拱肋、横撑的钢管厚度。

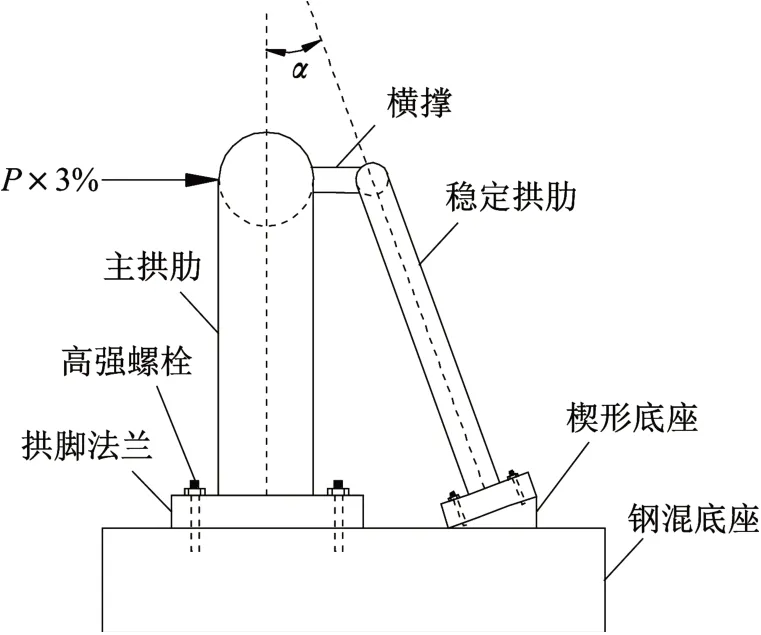
图2 试验模型侧视图Fig.2 Side view of experimental model

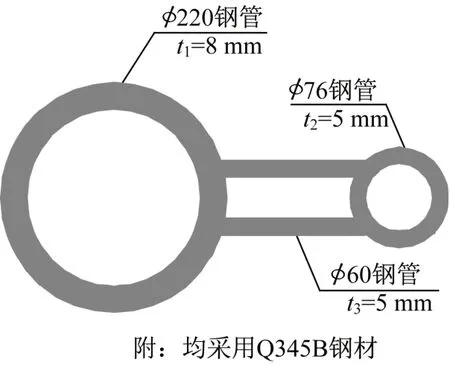
图3 拱顶截面图Fig.3 Cross section at the top of the arch

表1 模型参数Table 1 Model parameters

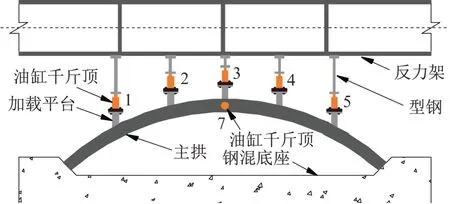
图1 试验模型正视图Fig.1 Elevation view of experimental model

1.2 加载方案

斜靠式拱结构试验装置主要由反力架、油压千斤顶、试验试件、测量装置等构成。在主拱肋的5个加载平台（每隔500 mm）分别设置竖向油压千斤顶，为提供初始缺陷在拱顶设置一个横向油压千斤顶，且其加载荷载数值设置为竖向油压千斤顶加载荷载数值的3%。此外，斜靠式拱结构与反力架之间的相对转动由油压千斤顶触头球铰实现。另外，为了在试验过程中实现斜靠式拱结构与反力架之间的相对位移不受约束，在油压千斤顶与反力架之间设置滚轴。斜靠式拱结构试验装置如图4所示。

图4 试验装置图Fig.4 Experiment setup

加载方案分为预加载与正式加载，两种加载过程均记录测量数据。其中，预加载至屈曲荷载理论值的20%。分4级加载，每级增加5%，持载3 min。通过预加载初步判断加载方式是否合理。对于正式加载，同样采取分级加载的方式，当加载小于屈曲荷载理论值的70%时，每级荷载按屈曲荷载理论值的10%增加，且每级持载时间为3 min，待稳定后记录数据；当施加荷载超过屈曲荷载理论值的70%且小于屈曲荷载理论值的90%时，每级荷载按屈曲荷载理论值的5%增加，且每级持载时间为3 min，待稳定后记录数据；当施加荷载超过屈曲荷载理论值的90%时，开始进行缓慢并且连续的加载，同时实时记录试验数据，预加载与正式加载的方案如表2所示。

表2 加载方案Table 2 Loading plan

1.3 测量方案

为了全面反映在五点竖向荷载P作用下斜靠式拱结构主拱肋的力学行为，三个斜靠式拱结构（α=10°、20°、30°）均在1～5号测点的截面下部布置竖向位移计测量该测点的竖向位移v，在其截面前部布置横向位移计测量该测点的横向位移w，如图5所示。此外，均在0～6号测点截面的上下左右四个位置处按逆时针方向布置应变片测量该处的应变ε，如图6所示。

图5 位移计布置图Fig.5 Layout of displacement meters

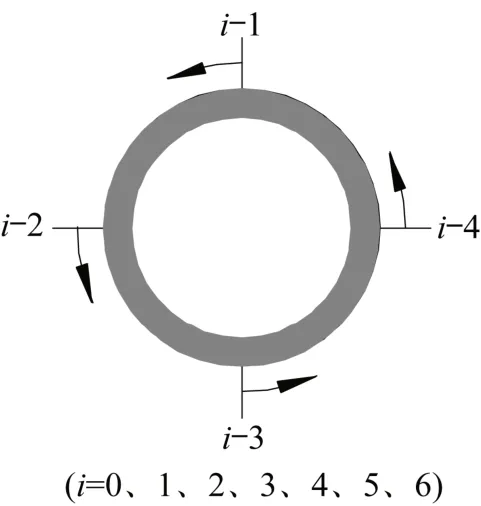
图6 应变片布置图Fig.6 Layout of strain gages

2 试验结果分析

通过试验测量得到多点竖向荷载作用下不同稳定拱肋倾角（α=10°、20°、30°）时斜靠式拱结构主拱肋竖向位移v、横向位移w以及纵向应变ϵ的相关数据。通过Matlab软件对数据进行处理，对实测数据进行对比分析。

2.1 位移分析

图7和图8分别为该工况荷载（P=300 kN）作用下以及不同稳定拱肋倾角（α=10°、20°、30°）时斜靠圆弧式拱结构主拱肋的竖向位移v与横向位移w的全跨分布图。其中，θ和Θ分别表示为圆弧拱系结构的角坐标与半圆心角。由图7可知，竖向位移v的绝对值随着稳定拱肋倾角α的增加而增加，且在拱顶位置处（θ/Θ=0）最大，表明稳定拱肋倾角α越大，斜靠圆弧式拱结构的竖向刚度越小；由图8可知，横向位移w的绝对值随着稳定拱肋倾角α的增加而减小，其同样在拱顶位置处（θ/Θ=0）最大，即稳定拱肋倾角α越大，斜靠圆弧式拱结构的抗侧倾能力越大。

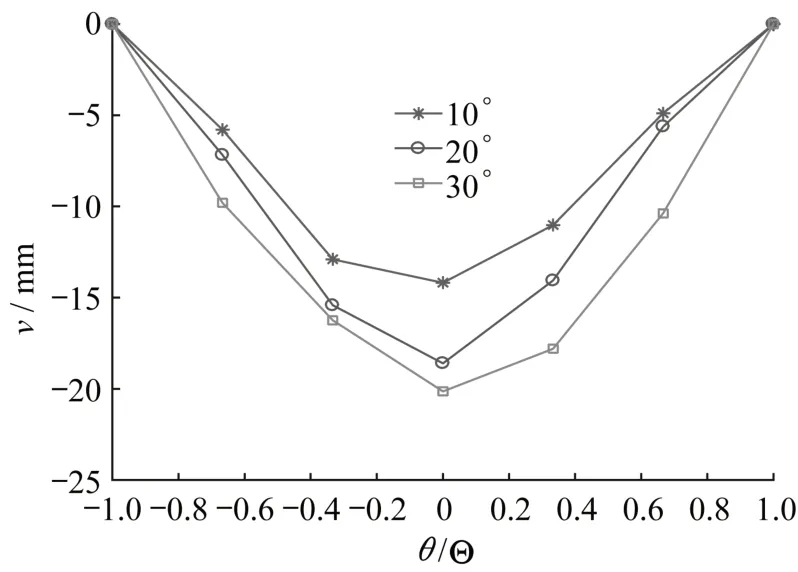
图7 全跨竖向位移Fig.7 Distribution of vertical displacementalong the main-arch

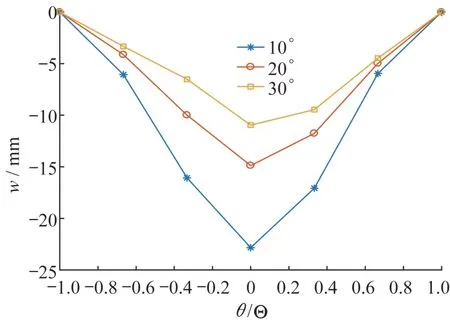
图8 全跨横向位移Fig.8 Distribution of horizontal displacementalong the main-arch

图9 和图10分别为在多点竖向荷载作用下稳定拱肋倾角α=20°时斜靠式拱结构主拱肋1～5号测点竖向位移v与横向位移w的变化图。其中，S表示为主拱肋弧长。从图9中可以看出：主拱肋的3号截面测点（S×3/6）处竖向位移v的绝对值最大；1号截面测点（S×1/6）与5号截面测点（S×5/6）竖向位移v的绝对值比较小，且两者较为一致；而2号截面测点（S×2/6）与4号截面测点（S×4/6）竖向位移v的绝对值也较为吻合，且大小居中。由图10可以看出，不同的竖向荷载P作用下斜靠式拱结构主拱肋1～5号截面测点横向位移w的变化规律与图9所得的竖向位移v的变化规律相似。同样在3号截面测点处横向位移w的绝对值最大；在1号截面测点与5号截面测点横向位移w的绝对值相近且比较小；在2号截面测点与4号截面测点横向位移w的绝对值相近且大小居中。表明斜靠式拱结构在失稳破坏过程中，拱顶位置的位移量最大，而拱脚位置的位移量最小。

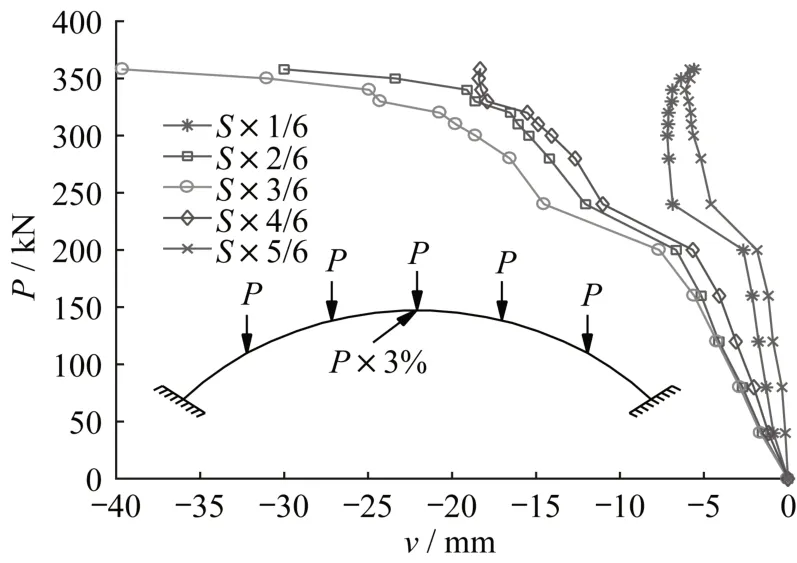
图9 竖向位移（α=20°）Fig.9 Distribution of vertical displacement atα=20°

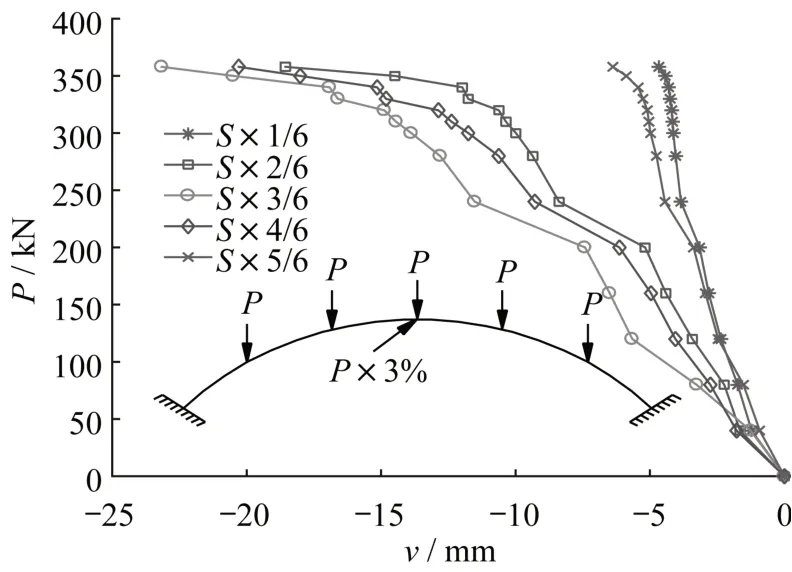
图10 横向位移（α=20°）Fig.10 Distribution of horizontal displacement atα=20°

图11和图12分别为多点竖向荷载作用下不同稳定拱肋倾角（α=10°、20°、30°）时斜靠式拱结构主拱肋3号截面测点竖向位移v与横向位移w的变化图。由图11可知：随着荷载P的增加，3号截面测点竖向位移v的绝对值增加；而随着稳定拱肋倾角α的增加，3号截面测点竖向位移v的绝对值增加；且稳定拱肋倾角α越大，斜靠式拱结构的临界失稳荷载越大。由图12可知：随着荷载P的增加，3号截面测点横向位移w的绝对值增加；而随着稳定拱肋倾角α的增加，3号测点横向位移w的绝对值减小。由图11和图12可以看出：稳定拱肋倾角α对斜靠式拱结构主拱肋横向位移w的影响比对纵向位移v大；且斜靠式拱结构的承载能力随着稳定拱肋倾角α增加而增强。

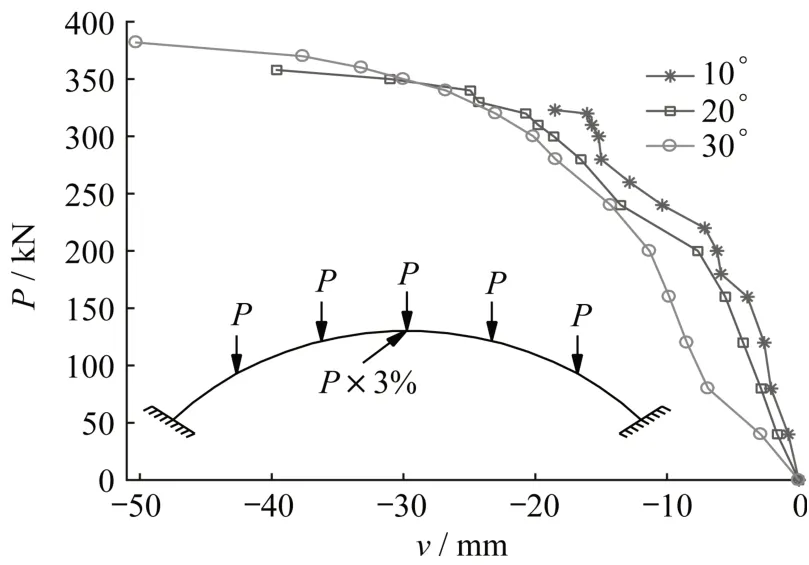
图11 竖向位移Fig.11 Vertical displacement

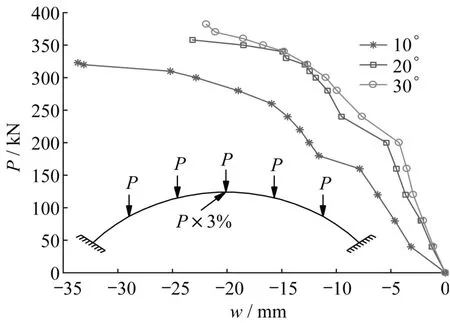
图12 横向位移Fig.12 Horizontal displacement

2.2 应变分析

图13 和图14分别为稳定拱肋倾角α=20°时多点竖向荷载作用下斜靠式拱结构主拱肋0～6号截面上缘测点应变ε的变化图以及3号截面上下左右四个测点应变ε的变化图。由图13可知：3号截面3-1测点处应变ε的绝对值最大，2、4、5、1、6、0号截面上缘测点应变ε的绝对值依次减小，且0号截面0-1测点与6号截面6-1测点的应变值较为一致，1号截面1-1测点与5号截面5-1测点的应变ε相近，2号截面2-1测点与4号截面4-1测点的应变值大小基本一致，表明了斜靠式拱结构变形对称均衡，结构缺陷较小，试验较为理想。由图13可知：3号截面上下左右四个测点（3-1、3-2、3-3、3-4）的应变ε不尽相同，其中3-1测点处应变ε绝对值最大，而3-3测点处的应变ε为正值，表明斜靠式拱结构在失稳破坏过程中，主拱肋拱顶截面的上缘变形最大，而下缘表现为受拉状态。

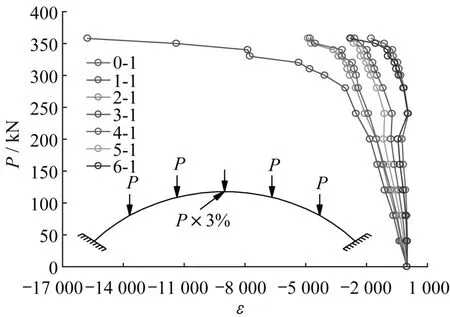
图13 全跨应变图Fig.13 Distribution of strain along the main-arch

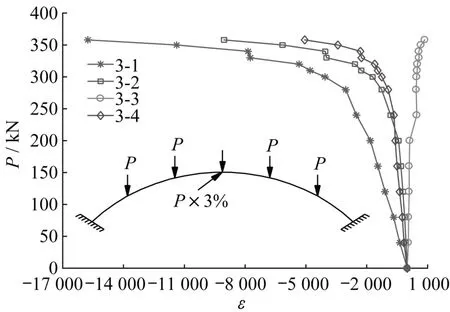
图14 拱顶截面应变Fig.14 Strain in the section at the top of the arches

图15 为不同稳定拱肋倾角（α=10°、20°、30°）时多点竖向荷载作用下斜靠式拱结构主拱肋3号截面3-1测点的实测应变ε变化图。从图15中可以看出：随着荷载P的增加，3号截面3-1测点应变ε的绝对值随之增加；而随着稳定拱肋倾角α增加，3号截面3-1测点应变ε的绝对值减小；并且同样可以看出稳定拱肋倾角α越大，斜靠式拱结构的承载能力越强。

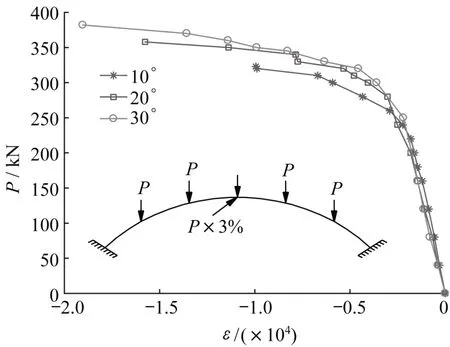
图15 拱顶应变图Fig.15 Strain at the top of the arch

3 结 论

本文对不同稳定拱肋倾角的斜靠式钢管圆弧拱结构进行多点竖向加载试验。通过试验测得的主拱肋竖向位移v、横向位移w以及应变ε，基于数据分析获得以下结论：

（1）当荷载相同时，斜靠式钢管圆弧拱结构的竖向刚度随着稳定拱肋倾角α增加而减小，其抗侧倾能力随着稳定拱肋倾角α增加而增强，且稳定拱肋倾角α对主拱肋横向位移w的影响大于对纵向位移v的影响。

（2）斜靠式拱结构主拱肋的拱顶截面上缘应变ε的绝对值随着稳定拱肋倾角α的增加而减小，且拱顶截面上缘测点处应变ε的绝对值最大。

（3）斜靠式钢管圆弧拱结构的极限承载能力随稳定拱肋倾角α的增加而增强。