An optimization method:hummingbirds optimization algorithm
ZHANG Zhuoran,HUANG Changqiang,HUANG Hanqiao,TANG Shangqin,and DONG Kangsheng
1.Aeronautics Engineering College,Air Force Engineering University,Xi’an 710038,China;2.Unmanned System Research Institute,Northwestern Polytechnical University,Xi’an 710072,China
1.Introduction
Optimization problems are common in science,economics,engineering,chemistry and other fields.However,in the face of increasingly complex optimization problems,especially high-dimensional ones with many local optimum points, gradient-based algorithms that use derivations of objective functions to direct the search are no longer applicable.
Stochastic algorithms optimize optimization problems randomly without substantial gradient information.Therefore, they are more suitable for complex optimization problems than gradient-based algorithms.In recent decades,stochastic algorithms have made great progress and have gradually replaced gradient-based algorithms to become the mainstream algorithms used for optimal calculations.
Stochastic algorithms include two main types:individual-based and population-based algorithms.Individual based algorithms generate only a single random solution and update during the whole optimization process.Although the algorithms have fewer function evaluations,the algorithms lack information sharing between individuals because of the small number of solutions,which makes it easy for the algorithm to fall into local optima.In contrast,population-based algorithms create multiple solutions randomly and ameliorate them during the course of optimization.Multiple solutions can enable population-based algorithms to search in different areas of space,and individuals can exchange information with each other.Therefore,compared with individual-based algorithms,population-based algorithms have the ability to jump out of local optima,at the expense of increasing the computational cost.
Most population-based algorithms have four basic characteristics:(i)they are nature-inspired;(ii)they use random variables;(iii)they do not require substantial gradient information;and(iv)they have several parameters that need to be tuned.According to the source of inspiration,the population-based algorithms can be divided into four categories:evolutionary,swarm intelligence-based,physics-based,and human behavior-based.Evolutionary algorithms are inspired by the evolutionary process of creatures in nature.The most representative algorithm is the genetic algorithm(GA)[1];it is based on Darwin’s theory of biological evolution,the main principle of which is survival of the fittest.Other popular algorithms are differential evolution(DE)[2],asexual reproduction optimization(ARO)[3],species co-evolutionary algorithm(SCEA)[4]and monkey king evolution(MKE)[5].
Swarm intelligence-based algorithms are inspired by the behavior of groups of creatures in nature.The most representative algorithm is particle swarm optimization(PSO)[6],which mimics the flocking behavior of birds.Other popular algorithms are cuckoo search algorithm(CS)[7],firefly algorithm(FA)[8],bat algorithm(BA)[9],grey wolf optimizer(GWO)[10],moth- flame optimization algorithm(MFO)[11],crow search algorithm(CSA)[12],cognitive behavior optimization algorithm(COA)[13],sperm whale algorithm(SWA)[14],grasshopper optimization algorithm(GOA)[15],and satin bower bird optimizer(SBO)[16].
Physics-based algorithms are inspired by physical rules in the universe.The most representative algorithm is gravitational search algorithm(GSA)[17],which works on the laws of gravity and mass interaction.Other popular algorithms are galaxy-based search algorithm(GbSA)[18],kinetic gas molecules optimization algorithm(KGMO)[19],water evaporation optimization(WEO)[20]and electrosearch algorithm(ES)[21].
Human behavior-based algorithms are inspired by the social behavior of human beings.The most representative algorithm is teaching-learning-based optimization(TLBO)[22],which simulates the teaching behavior of teachers and the learning behavior of students in a classroom.Other popular algorithms are harmony search(HS)[23],interior search algorithm(ISA)[24],human behavior-based optimization(HBBO)[25]and human mental search(HMS)[26].
For the vast majority of population-based algorithms,how to more effectively balance exploration and exploitation is the key to improving the performance of the algorithms.Exploration represents the global search ability of population-based algorithms,and it is employed to enhance the ability to jump out of local optima by searching in new regions with some randomization method.Meanwhile,exploitation can improve the convergence speed of population-based algorithms,and it is applied to find a better solution in the vicinity of the current optimal solution.However,these two capabilities are conflicting,and no one knows the exact proportion of the two in the algorithm for any optimization problem.The existing viable balancing strategies can be grouped into three categories:(i)The initial phase of the algorithm is searched globally and locally searched later.(ii)Better individuals perform local search,and poor individuals perform global search.(iii)Global search and local search are randomly switched at a certain probability in the algorithm.
Moreover,almost all population-based algorithms contain several parameters that need to be tuned before runs.For example,DE requires scaling and crossover factors to be pre-set.HS should consider the value of the harmony memory considering rate,the pitch adjusting rate and the bandwidth of generation.PSO needs to determine the inertia weight,the maximum value of velocity,the cognition factors and the social learning factors.For different optimization problems,the algorithm often needs to set differentparameter values. This is time-consuming work.Therefore,compared to algorithms with multiple control parameters,an algorithm with fewer parameters is easier to implement and more adaptive to a wider variety of optimization problems.
Despite a variety of new algorithms emerging in an endless stream,the no-free-lunch theorem[27]has proven that no single algorithm can solve all optimization problems.In other words,if an algorithm performs well for some issues,it will inevitably perform poorly for other problems.Therefore,there are still many specific optimization problems that need to be addressed by new algorithms instead of the current optimization techniques.For this reason,a population-based algorithm named the hummingbirds optimization algorithm(HOA)is proposed to solve optimization problems.The algorithm is inspired by the foraging process of hummingbirds.
The rest of the paper is organized as follows:The mathematical model of HOA is described in detail in Section 2.Section 3 describes the experimental setting and demonstrates the experimental results.Eventually,the conclusion and suggestions for further work are presented in Section 4.
2.HOA
2.1 Inspiration
Hummingbirds are the smallest birds in the world,and most of them are 7 cm to 13 cm long.This unique bird is only distributed in the Americas,and the habitat of the vast majority of species is in tropical and subtropical Central America.Hummingbirds can fly at a speed of up to 45 km per hour.They can hover in mid-air at rapid wingflapping rates,which vary from approximately12beats per second in the largest species to in excess of 80 in some of the smallest[28].Hummingbirds need to rely on foraging to maintain the body’s high metabolism,and their main food comes from nectar.Fig.1 shows a hummingbird in nature.

Fig.1 A real hummingbird who is gathering nectar
There are two search phases during the foraging process of hummingbirds.The first is the self-searching phase.In this phase,the hummingbird can search according to its cognitive behavior without interacting with other indivi-duals in the population[29,30].Essentially,cognitive behavior is a selective search process that is based on the search experience accumulated by an individual.For example,hummingbirds often perform a targeted search using their experience and can thus anticipate the amount of nectar in flowers according to their shape or color.If the amount of nectar is determined to be plentiful,the hummingbird will further exploit this flower.However,they will quickly leave a flower and randomly search for the next target if it is not plentiful.It is undoubtedly a simple and effective search model when hummingbirds lack explicit information about food location.
The second is a guide-search phase.In addition to searching through experience,hummingbirds can also search by using various dominant individuals as guidance information.For example,in the territorial behavior of hummingbirds,after an individual occupies a rich food source as its territory,other hummingbirds will move rapidly to the territory [31,32].When these new arrivals are driven away by the first individual,they will follow other outstanding individuals.The advantages of this mode are to help hummingbirds have a clear searching direction and avoid blind searching.
Inspired by these two search phases,we propose a new optimization algorithm,the HOA,whose details are described in the next section.
2.2 Proposed method description
As described above,our HOA includes two phases:a self searching phase and a guide-searching phase.The hummingbirds in HOA represent searchers,and their positions are corresponding to feasible solutions of the optimization problem.The quality of food sources are the values of the fitness functions,and the best food source is the optimal solution.The initialization of HOA is done by the following formula:

wherePiis the position of theith hummingbird in the population(i∈{1,2,3,...,N},Nis the population size),andubandlbrepresent the upper and lower bounds of the variables in the search space,respectively.randis a random number between 0 and 1,and it has the same meaning in the following paragraphs.
2.2.1 Self-searching phase
To convert the cognitive behavior into a mathematical model,we treat the last preserved solution of the algorithm as the experience of the current search.When hummingbirdicontinuously finds better sources of foodit means that the current search area is promising.
Thus,the hummingbird will exploit the area further.The new position of hummingbirdican be obtainedvia the following formula:
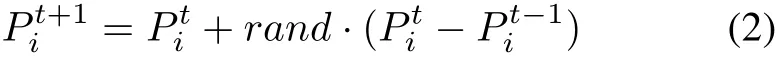
whereare the positions of theith hummingbird at iterationtandt-1 respectively.is accepted if it gives a better function value,otherwise it keeps unchanged.
When hummingbirdisearches continuously,but fails to find better resultsit means that the hummingbird will know from experience that the current area is not worth continued exploitation.In this case,the hummingbird will randomly change the search direction.This procedure is implemented based on Levy flight. Levy flight is an important non-Gaussian random walk whose random step is subject to a heavy-tailed probability distribution[33].Due to the in finite and rapid growth of variance,the most important feature of this flight mode is that it can search the space to the greatest extent possible in an uncertain environment.Levy flight is more efficient for searching than regular random walk or Brownian motion.Fig.2 exhibits the movement tracks of 1 000 steps of Levy flight and Brownian motion in two dimensions.
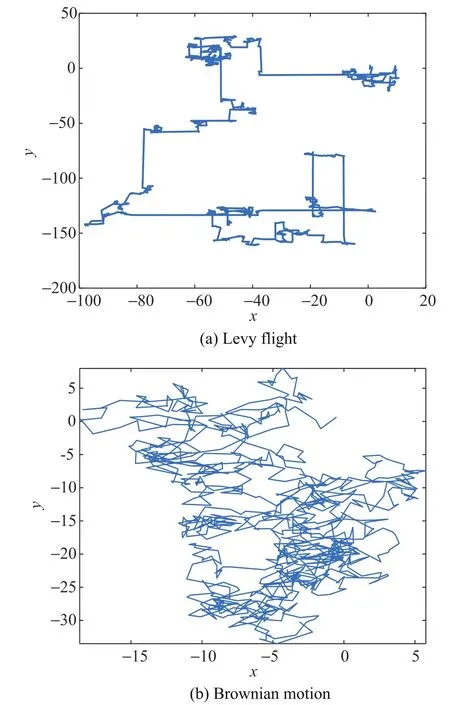
Fig.2 Comparison of the movement tracks of Levy flight and Brownian motion in two dimensions
As shown in Fig.2,we can observe that Levy flight generates larger jumps than the Brownian motion and thereby explores the search space more broadly.Therefore,it is more suitable for large-scale search.
The new positions of hummingbirds are generated by performing Levy flight,as described as follows:

whereαis a scale factor that should be related to the scales of the problem of interest.The⊕is the entry-wise multiplications.Acceptif it gives a better fitness value.
According to[7,34],αand Levy(β)can be formulated as

In the self-searching phase,hummingbirds generally learn according to the original gradient information,which can accelerate the convergence speed of the algorithm.However,when the algorithm may fall into a local optimum,the hummingbirds search extensively through Levy fl ight in the search space,which can enhance the global search capability of the algorithm.
2.2.2 Guide-searching phase
In this phase,the humming birds search in the environment by territorial behavior.The current best individual in HOA that occupies the territory is called the territory bird.The other individuals are called following birds. The position of the territory is the same as the position of the current optimal individual.After occupying the territory,the territory bird patrols around its territory ceaselessly.This process can be described as follows:
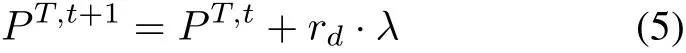
wherePT,tis the position of the territory birdat thetth iteration.rdis a random value between–1 and 1,which can adjust the search direction of the individual.λis a scale factor that make the territory bird move slightly around its current position.Here,λis set to 0.1(ub-lb).PT,t+1will replacePT,tif its fitness value is better thanPT,t.Equation(5)is aimed to adding a slight perturbation to the best individual,allowing it to perform a fine search within its neighborhood.This method can help the best individual jump out of the local optimum,thus avoiding the stagnation of the evolution of the algorithm.
Different from the territory bird,the movement of the following birds is divided into two states.
State 1The territory bird does not find the approaching following birdj.In this case,the following birdjwill move to the territory bird.Its new position is updated as follows:
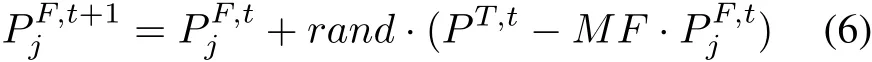
whereis the position of thejth following bird at thetth iteration.MFis a mutation factor that can decide if the position of the following bird is to be changed.The value of this factor is 1 or 2,which is again a heuristic step selected randomly by equal probability asMF=round[1+rand{2-1}].As the population gradually converges in the search space,will approachIn the later stage of convergence,it is assumed that,then(6)can be transformed into the following forms:
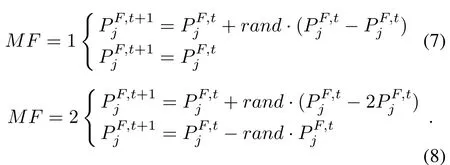
From(7),it can be found that,will always bewhenMF=1.Meanwhile,(8)shows that the population remains exploratory and allows for exploration away from the spatially converged solutions.Based on the above analysis,MF can effectively balance the local search ability and global search ability of the algorithm.
State 2The territory bird finds the following birdjclose to itself and issues warnings.The following birdjis frightened and flies to the surrounding area. In this process,an individual is randomly selected from the other following birds.If the selected individual has a better position,the following birdjflies towards it.However,if the selected individual has a worse position,it is better to move away from that individual.This process is described by the following formula:
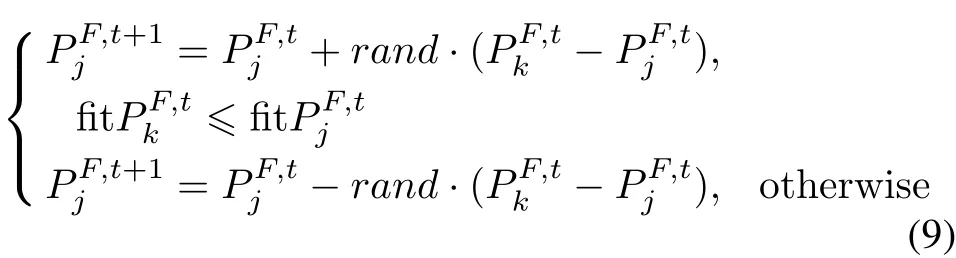
wherej,k∈{1,2,3,...,N-1},j/=k.
Combining the two states,the movement pattern of the following birds can be described as follows:

wherePFtdenotes the probability that the following birds are found by the territory bird.In this work,PFtis determined as follows:

To avoid being trapped into local optima,a role-switch mechanism during the search process is introduced:if a following bird finds an area that is better than that currently occupied by both other following birds and the territory bird,it will be converted into the new territory bird,and the original territory bird will be converted into a following bird in the next iteration.
In addition,individuals in HOA may search beyond the borders.Therefore,we add a border control strategy,whose specific process is as follows:

whereis thedth dimension of theith solution at thetth iteration.To sum up,the pseudo code of the HOA can be given as in Algorithm 1.
Algorithm 1HOA pseudo code


3.Experimental study
In total,ten classical benchmark functions and two well known engineering design optimization problems are employed to integrally evaluate the performance of HOA.All experiments are performed in the MATLAB 2016a software,and the simulations are run on a Core(TM)i7-6700HQ 2.60 GHz with 16 GB RAM.
3.1 Experiment I:unconstrained benchmarks
In this section,ten different benchmark functions,as given in[35],are used to evaluate the performance of HOA,and their results are compared with the results of 11 algorithms in two groups.In the first group,three classical and mainstream algorithms that have been applied in many fields,i.e.,PSO[36],artificial fish swarm algorithm(AFSA)[37],artificial bee colony(ABC)algorithm[38]are used.In the second group,eight state-of-the art algorithms that have been proposed in the recent literature:CS[7],GSA[18],FA[8],GWO[10],MFO[11],CSA[12],sine cosine algorithm(SCA)[39]and SBO[16]are employed.The benchmark functions include two categories:unimodal(f01–f05)and multimodal(f06–f10).The detailed information for the ten benchmarks is summarized in Table 1. The maximum number of function evaluations(MaxFEs)is set to 100 000 forf01–f10.Each algorithm is performed independently for the test functions 30 times.
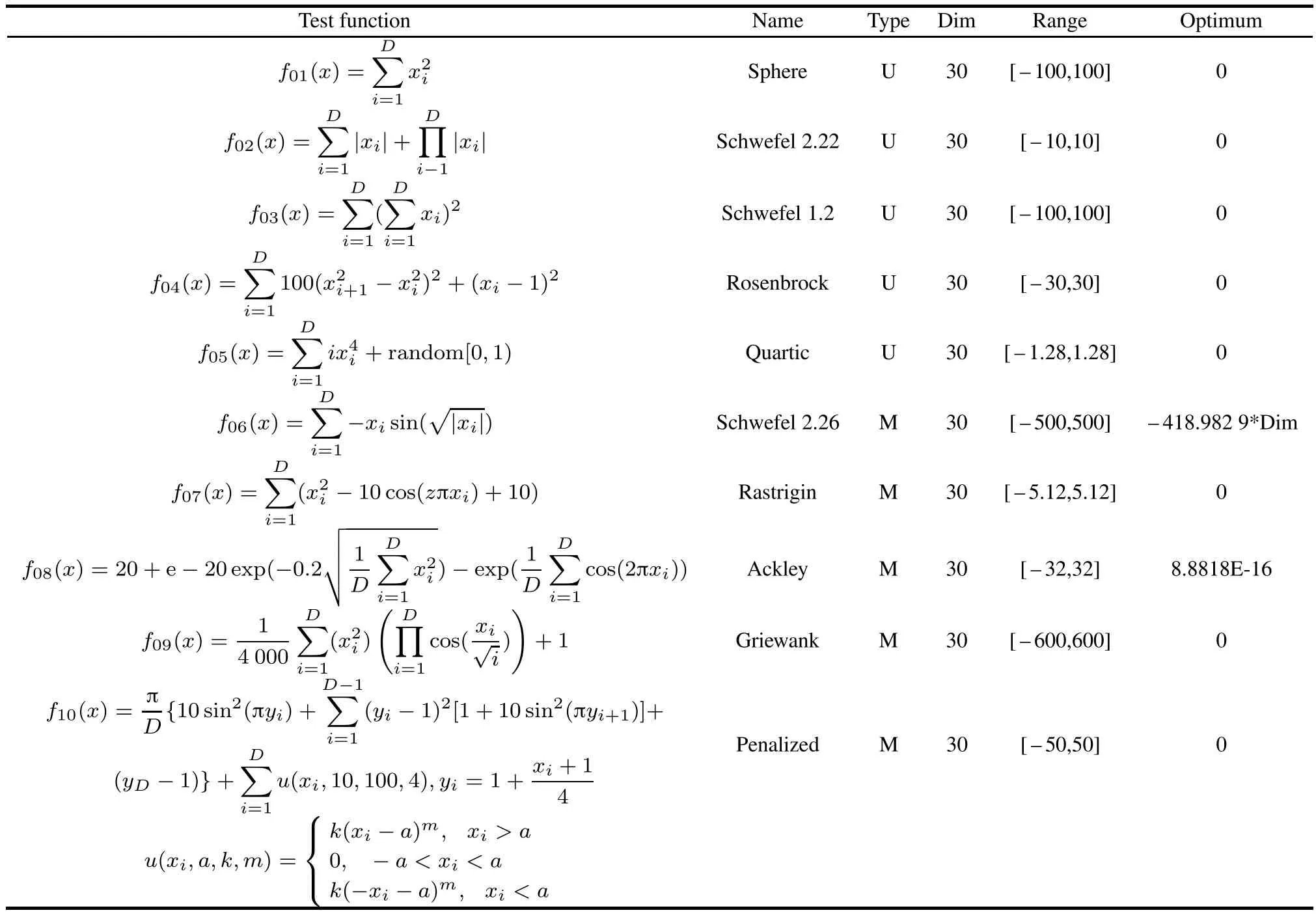
Table 1 Description of the benchmark functions(U:unimodal;M:multimodal;Dim:dimension)
First,we compare HOA with mainstream algorithms in the first group.For a fair comparison,to compare all algorithms under the same number of maximum iteration for each test function,the population size of the HOA is set to 50 because it has two phases,and the population size of the other algorithms is set to 100 because of the inclusion of one phase.The control parameter settings for the compared algorithms in this test are detailed as follows:
(i)PSO:ωmax=0.9,ωmax=0.4 andc1=c2=2 as in[36];
2) 将液压千斤顶进行升压,加载油压升压到23.89 MPa,系统稳定15 min后输入150 t,标定满量程。
(ii)AFSA:Visual=1,Step=10,try number=100 andδ=0.618 as in[37];
(iii)ABC:limit= (N·D)/2;size of employed bee=onlooker bee=(colony size)/2 as in[38].
Table 2 shows the optimization results obtained using the HOA and three compared algorithms over unimodal functions(f01–f05),where“Best”,“Worst”,“Mean”,and“SD”,respectively,denote the best,worst,and mean fitness values with the standard deviation.Moreover,the algorithms are sorted on the mean solution from small to large,and the best results are highlighted for each function with boldface font.Finally,to intuitively exhibit the performance of the three algorithms,we add the average ranks and the over all rank in Table 2.According to Table2,it can be observed that our HOA has the best results among the compared algorithms,and the convergence curve shown in Fig.3 indicate that HOA has the fastest convergence speed.
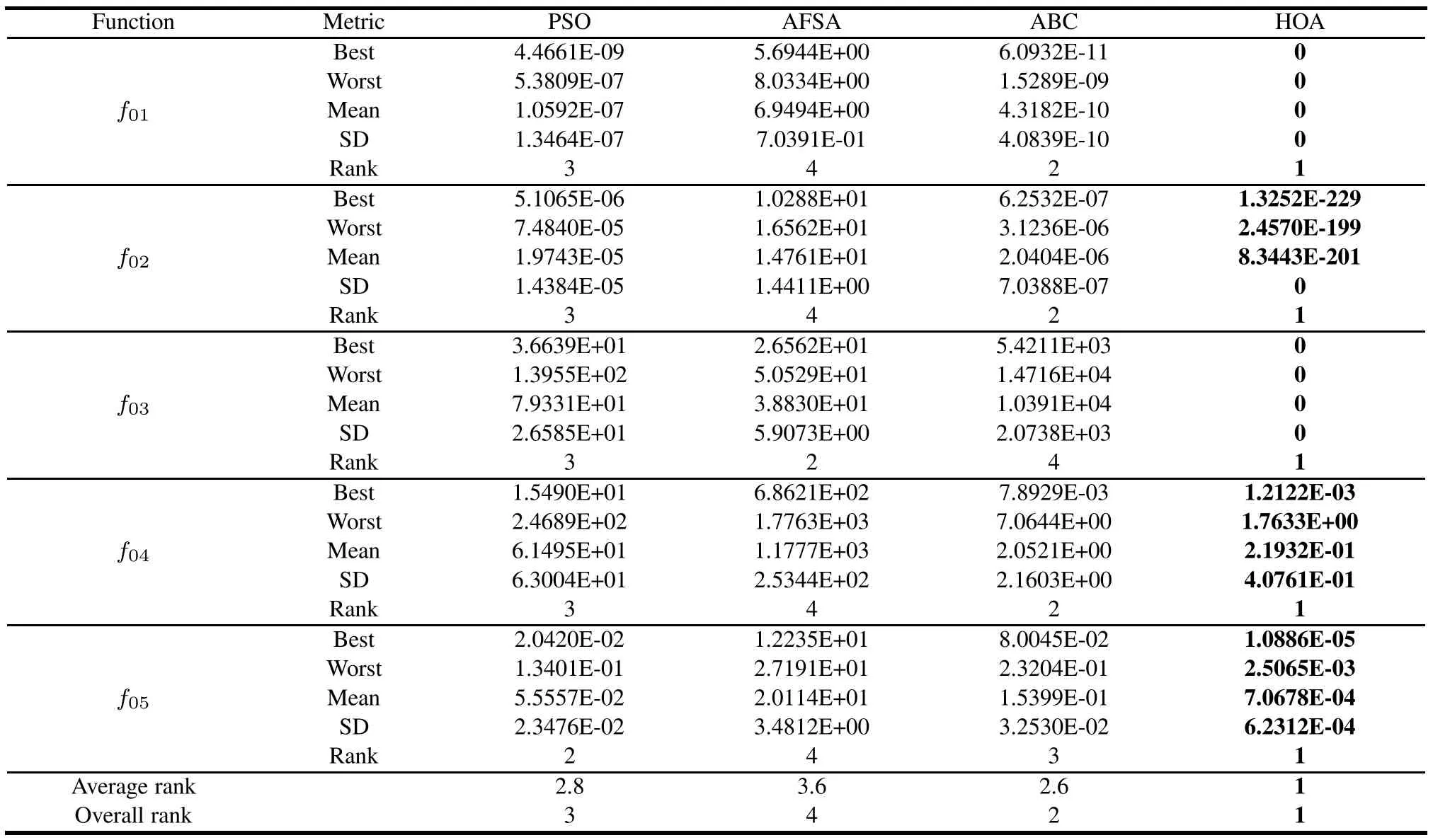
Table 2 Statistical results of five unimodal functions for four algorithms

Fig.3 Convergence graphs of four unimodal functions for PSO,AFSA,ABC,and HOA
The comparative results obtained by all algorithms for the multimodal functions(f06–f10)are summarized in Table 3.Unlike the unimodal functions,multimodal functions include many local minima,the number of which increases exponentially as the problemsize increases.Therefore,these functions can undermine the exploration capability of the optimizers.From Table 3,we can find that HOA outperforms other algorithms on functions(f07–f10)and only loses inf06.Forf06,ABC exhibits the best performance and HOA shows the second best performance.From the last row of Table 3,HOA ranks first among all the algorithms.As the convergence curves of all algorithms shown in Fig.4,HOA presents the promising performance in the convergence speed.
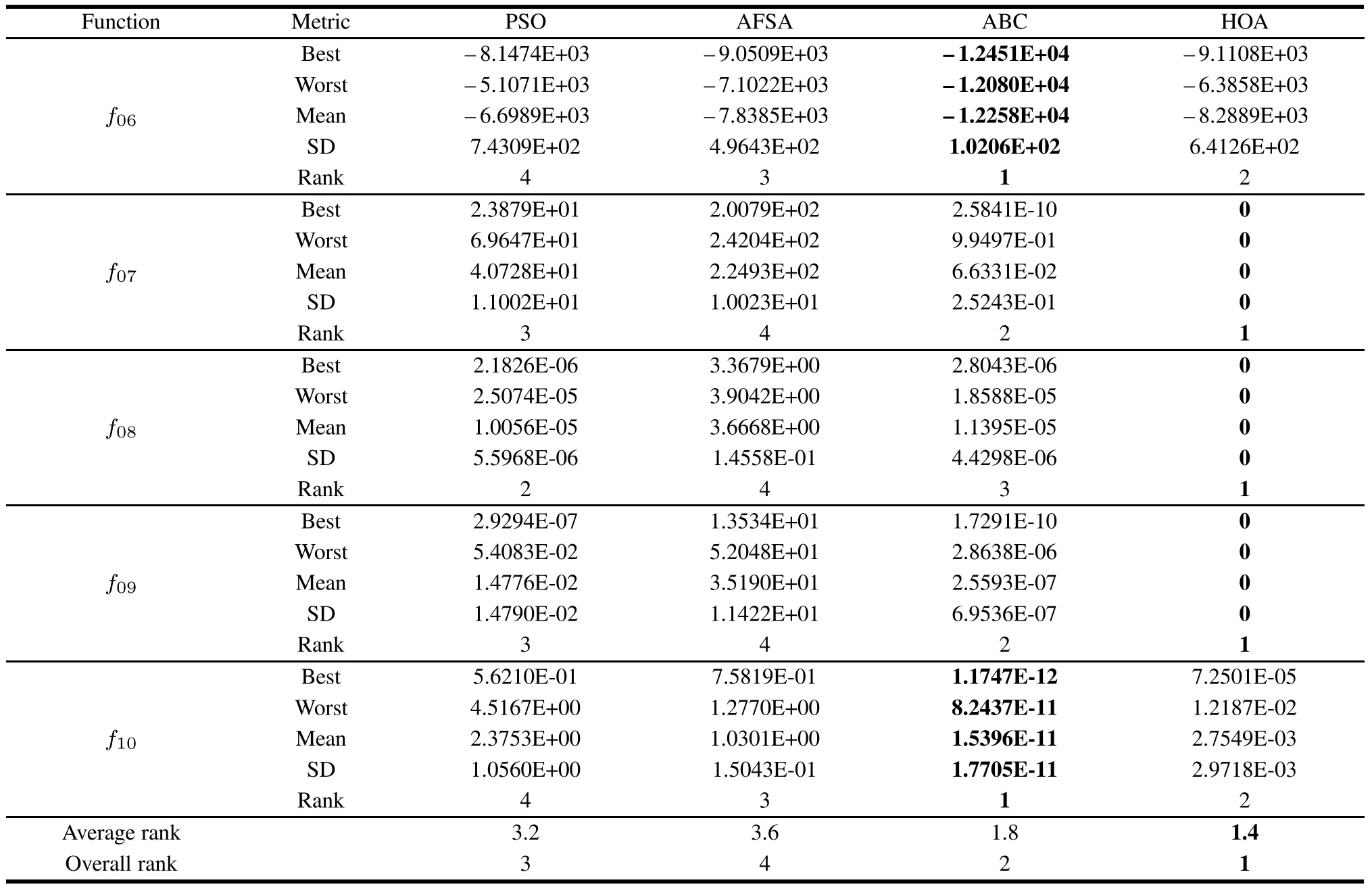
Table 3 Statistical results of five multimodal functions for four algorithms
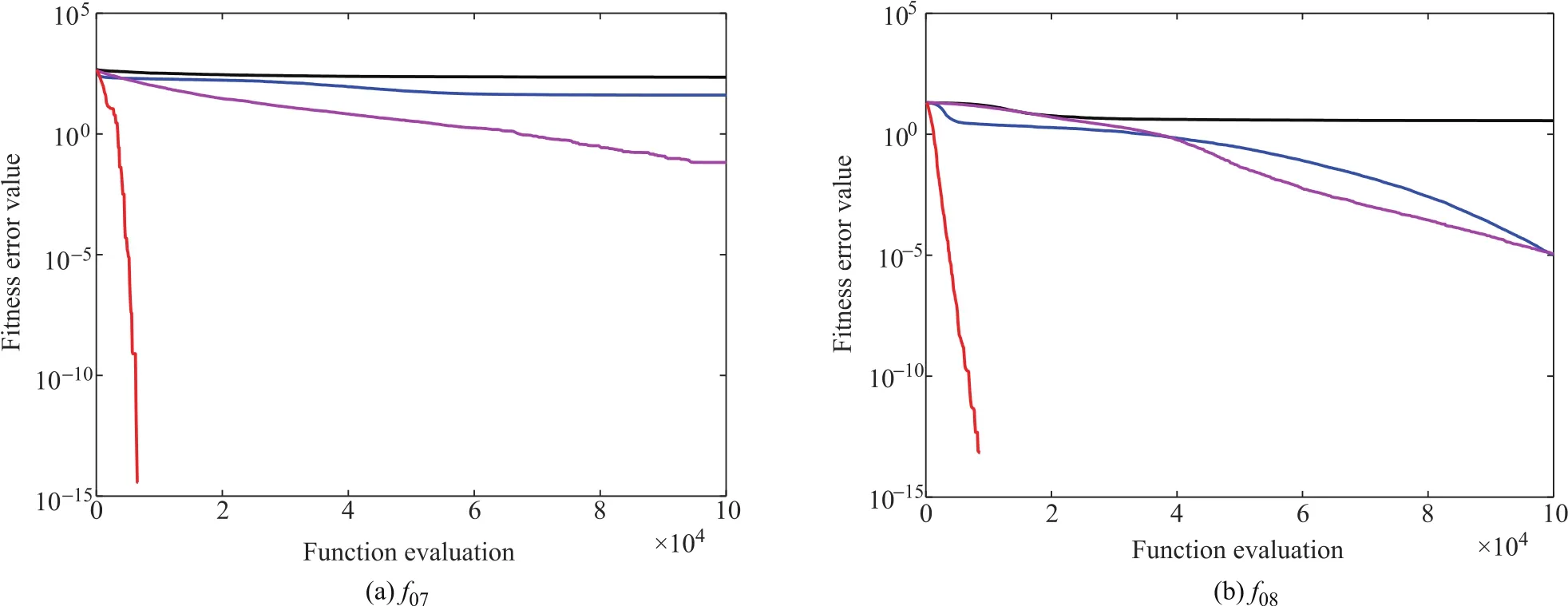
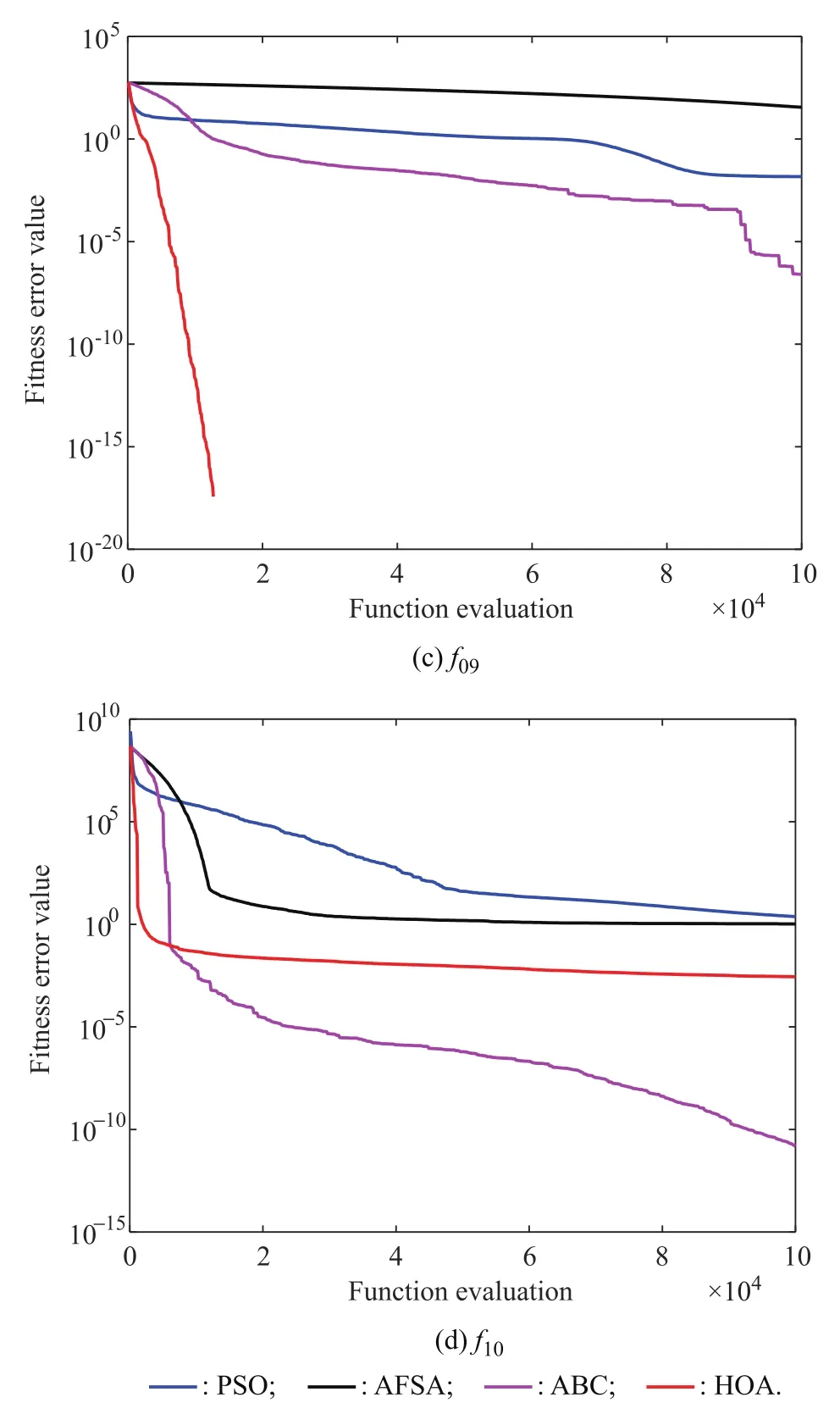
Fig.4 Convergence graphs of four multimodal functions for PSO,AFSA,ABC,and HOA
In order to further test the performance of the algorithm,the HOA is compared with the second group of advanced algorithms.To ensure the fairness of comparison, the population size of HOA and CS is set to 50 because they have two phases.For the remaining algorithms,the population size is equal to 100because they have only one phase.Specific control parameters are not required for the HOA,and the control parameters settings for all compared algorithms are described in Table 4.

Table 4 Control parameters of eight compared algorithms
Table 5 provides the statistic results obtained by the nine algorithms for unimodal functions(f01–f05).From Table 5,we can observe that HOA can achieve better results than the other companion algorithms forf01–f04and is worse only forf05.The last row of Table 5 shows that HOA ranks first among all algorithms.GWO has promising performance forf05and ranks second compared with the other algorithms.The graphical results of the convergence rate and analysis of variance(ANOVA)test given in Fig.5 indicate that HOA outperforms its competitors in terms of convergence rate and solution quality.

Table 5 Statistical results of five unimodal functions for nine algorithms
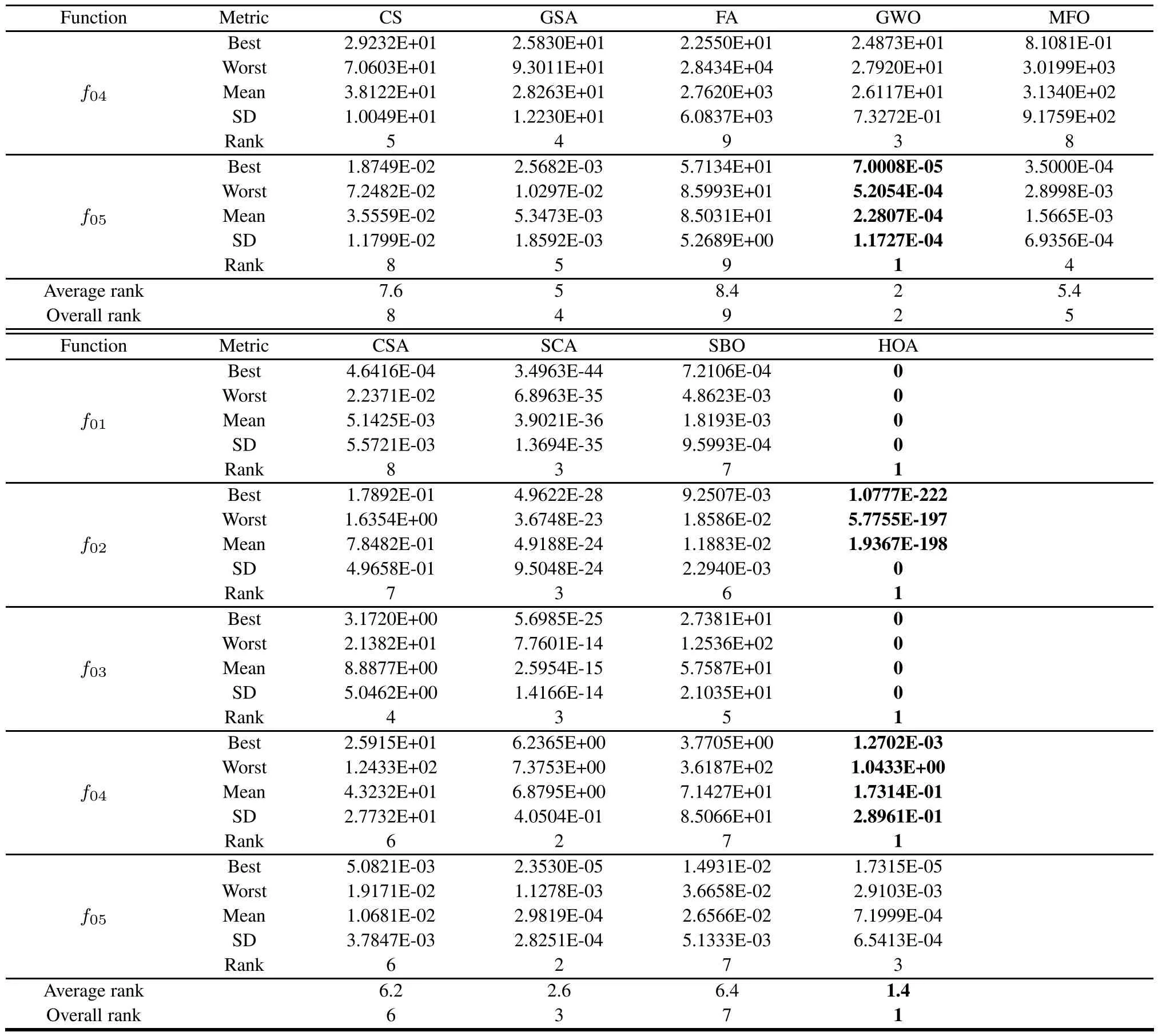
Continued

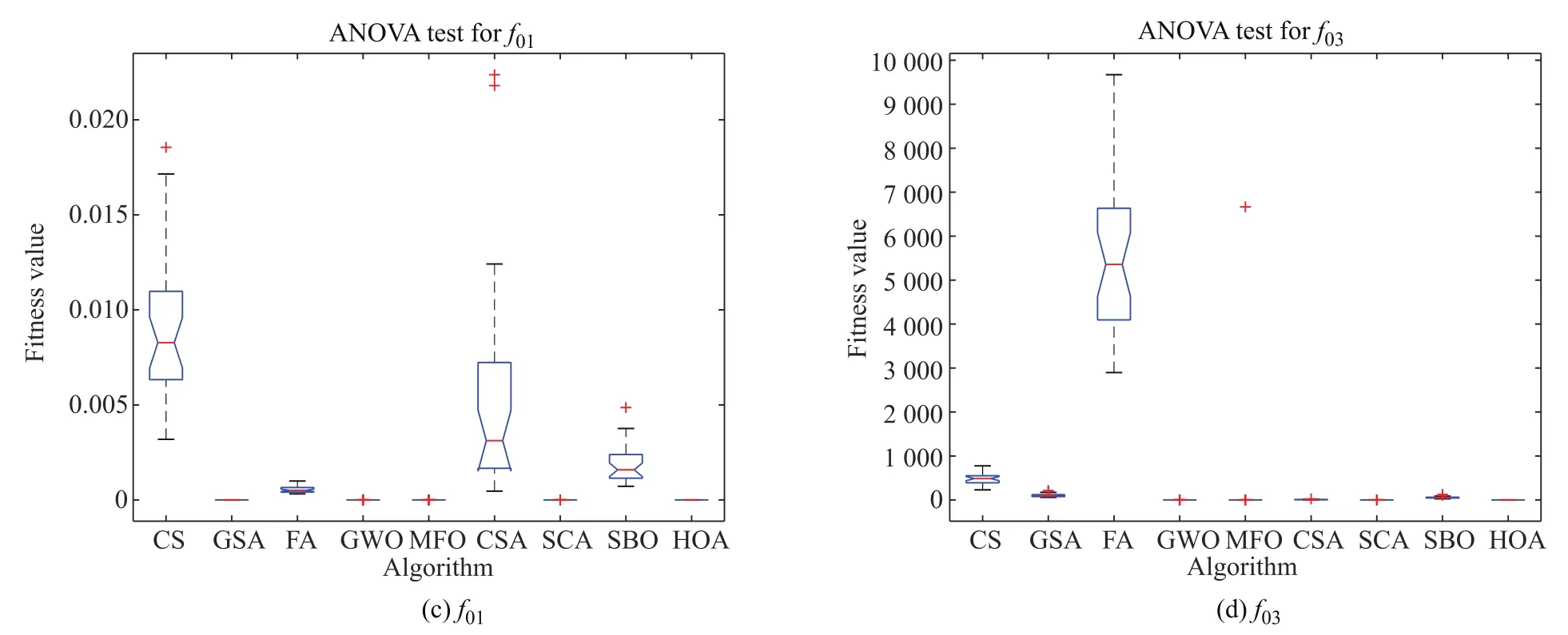
Fig.5 Convergence curve and ANOVA test of four unimodal functions
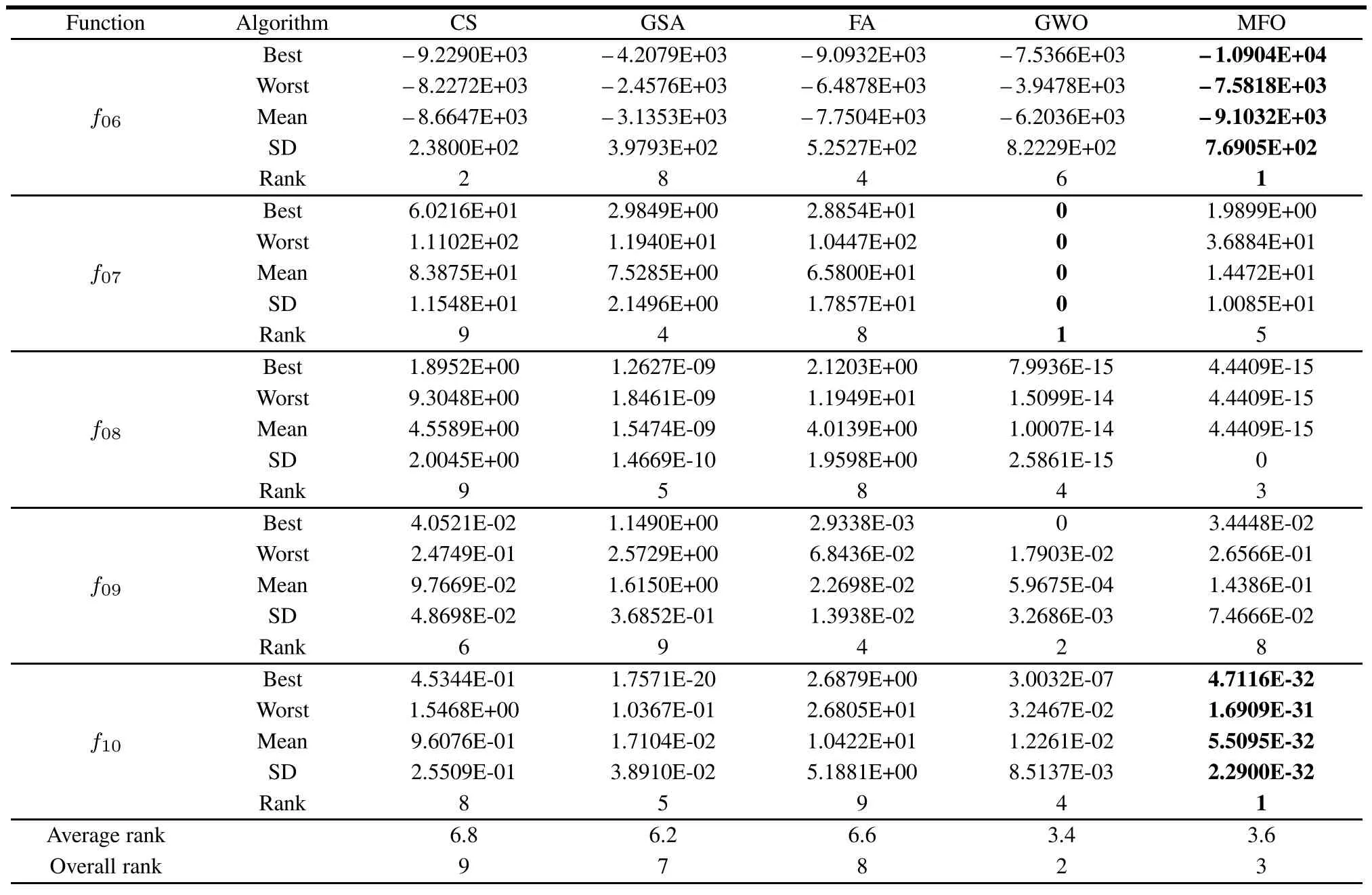
Table 6 Statistical results of five multimodal functions for nine algorithms

Continued

Fig.6 Convergence curve and ANOVA test of four multimodal functions for different algorithms
Table 7 presents the statistical results of the Wilcoxon signed ranks test[40]at the 95%significance level for ten functions.As a nonparametric test,the Wilcoxon signed ranks can detect whether there is a significant difference between HOA and each compared algorithm.In Table 6 and Table 7,“+”means that HOA is significantly better than the other algorithm,and“–”means the opposite.“≈”indicates that HOA is not significantly different from the competitor.“R+”indicates the sum of ranks for which HOA exceeds the corresponding competitor,and“R–”denotes the sum of ranks for the opposite.From the results of“+/≈/–”of Table 5 and Table 6,we can observe clearly that HOA obtains a greater number of“+”than the other algorithms,which means that HOA shows a statistically excellent performance compared to its competitors in the Wilcoxon signed ranks test.
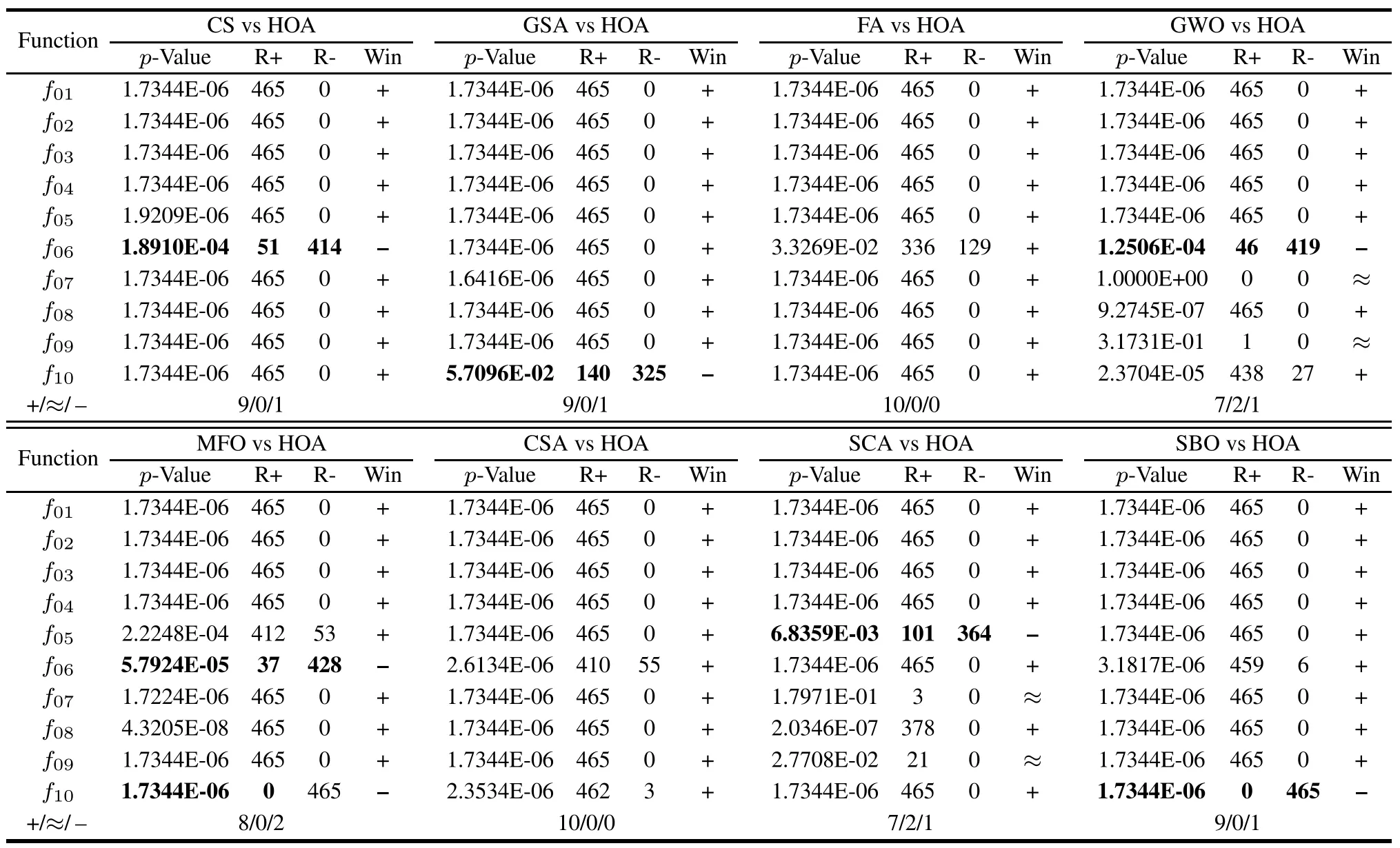
Table 7 Results of a Wilcoxon signed ranks test based on the best solution for each function with 30 independent runs(α=0.05)
In general,HOA is faster than other algorithms in terms of convergence speed,due to full use of its own gradient information and global optimal individual information,which effectively improves the local exploitation capability of the algorithm.In addition,HOA also gets its own superiority in search accuracy.The main reason of that is that HOA contains two random search strategies:Levy flight strategy and random escape strategy,which enhance the exploration ability of the algorithm.At the same time,we can note that CS,FA,AFSA perform poorly among the above-stated methods.This is because the mutation of the CS algorithm is single,and the control parameters of the FA and AFSA algorithms are more difficult to adjust.Therefore,the combination of multiple mutation methods and the minimal control parameters may be the focus of future research on optimization algorithms.
3.1.1 Search behavior analysis of HOA
To study the influence of the self-searching phase and the guide-searching phase,in this section,the proposed algorithm is compared with two different algorithms:(i)HOA without the self-searching phase(denoted HOA-S)and(ii)HOA without the guide-searching phase(denoted HOA-G).In addition,the population of the two tested algorithms is set to 100 because each of them has only one phase.These two algorithms and the standard HOA are tested by six typical functions from the above classic benchmark functions.The statistical results of 30 runs for all algorithms are presented in Table 8,and the convergence rates for each algorithm for four functions are depicted in Fig.7.

Table 8 Statistic results of HOA-S,HOA-G and HOA

Fig.7 Convergence curves of HOA-S,HOA-G and HOA for different benchmarks
According to Table 8 and Fig.6,we can easily draw several significant conclusions:First,HOA outperforms HOA-S and HOA-G in terms of accuracy and convergence rate,which means that the coexistence of the self-searching phase and the guide-searching phase is very important.Second,the performance of HOA-G is the worst among all algorithms,which suggests that the guide-searching phase has the greatest impact on the performance of HOA.Finally,although the impact of the self-searching phase on the algorithm is far less than that of the guide-searching phase,the former also has important effects on the performance of HOA.In general,the two phases influence the final optimization results of the algorithm to different degrees.When the two phases coexist,the algorithm is better at solving the optimization problem.Therefore,each behavior is essential for HOA.
3.1.2 Computational complexity of the HOA
The computational complexity of our HOA relies on the population sizeN,dimension of the problemD,maximum number of iterationsT,and sorting mechanism of the following birds in each iteration.During one iteration,the time complexity of all individuals update and border control strategy in the self-searching phase of HOA isO(2ND).In addition,in the guide-searching phase of HOA,the time complexity of the territory bird update and border control strategy isO(2D);the time complexity of probabilityPFtisO((N-1)2);the time complexity of the following birds update and border control strategy isO(2(N-1)D).Based on the analysis of the above,the overall computational complexity of HOA is defined as follows:
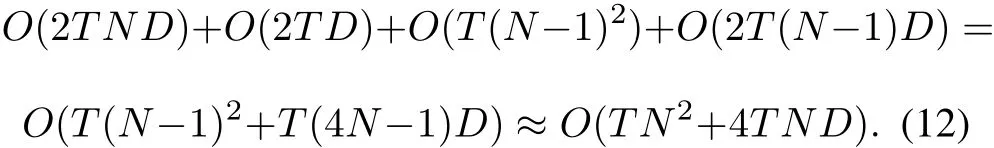
Table9lists the comparisons of computational complexity of HOA and several representative algorithms in our experiments.From Table 9,we can observe that the computational complexity of CSA is the smallest,and it is followed by the PSO and CS.Although the HOA ranks fifth,it is better than the ABC and GSA.However,based on the promising performance for the ten benchmarks,the computational complexity of the HOA is acceptable.

Table 9 Comparison of the computational complexity of seven algorithms
3.2 Experiment II:engineering design problems
Two well-known engineering design optimization problems,the three-bar truss design problem and the welded beam design problem,are chosen as constrained functions to further examine the performance of HOA.The penalty functions are used as constraint handling mechanisms because they are the simplest and have the lowest computational cost.The population size of HOA is set to 50,and the statistical results of HOA for each engineering problem are obtained in 30 independent runs.
3.2.1 Three-bar truss design problem
The three-bar truss design problem is a famous structural design problem in practical engineering applications,and is often used to assess the performance of different algorithms.A pictorial illustration of some components of the design problem is given in Fig.8 There are two structural variables,which are cross-sectional areas(A1andA2).This problem aims to acquire the least weight,but it also needs to be subject to several constraints,such as stress,deflection,and buckling constraints.The problem is formulated as follows:
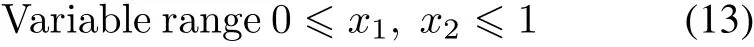

Fig.8 Schematic of the three-bar truss design problem
Table 10 presents the comparisons of the best optimization results obtained by HOA and several previous methods.To date,this problem has been dealt with by numerous optimization algorithms,including:society and civilization(SC)[41],hybrid evolutionary algorithm and an adaptive constraint-handling technique(HEA-ACT)[42],DE with dynamic stochastic selection(DEDS)[43],PSODE[44],CS[45],mine blast algorithm(MBA)[46],and CSA[12].The comparisons of statistical results for HOA and the above mentioned optimizers are shown in Table11.From Table 11,it can be found that the best result is 2.638958433764684E+02 with only 13 000 function evolutions(FEs),which is the lowest among all methods.Specially,for the mean or standard deviation,even the worst value of our HOA with 20 000 FEs is the smallest among all the algorithms,which indicates that HOA is more robust than the other reported optimizers.

Table 10 Comparison of the best solution found by various studies for the three-bar truss design problem
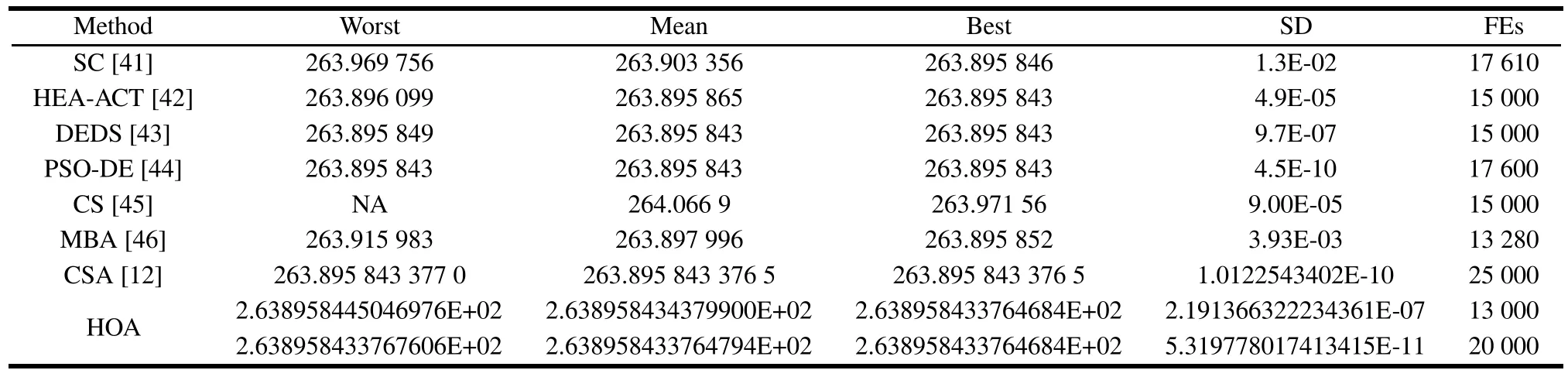
Table 11 Comparison of statistical results found by different approaches for the three-bar truss design problem
3.2.2 Welded beam design problem
As Fig.9 indicates,this problem includes four variables:the design thickness of the weldh,the length of the clamped barl,the height of the bart,and the thickness of the barb.The main purpose of this optimization process is to obtain the minimum cost of a welded beam subject to constraints such as weld stress,buckling load,beam deflection and beam bending stress.This problem can be expounded as follows:

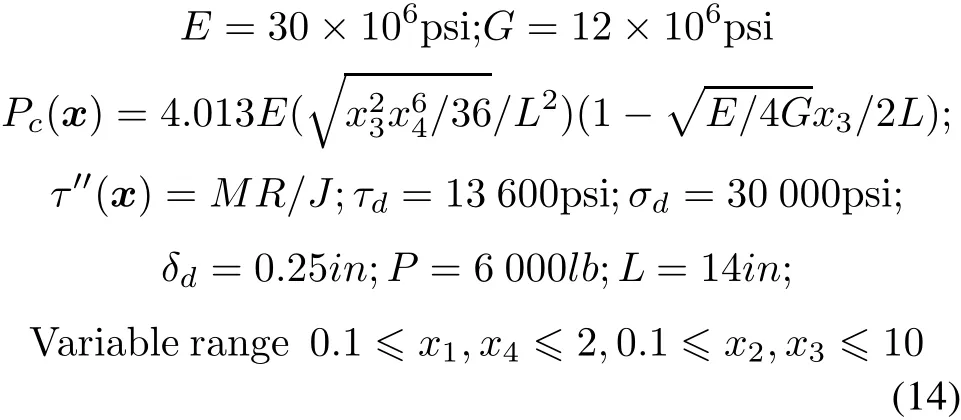

Fig.9 Schematic of welded beam design problem
Table 12 compares the best designresults given by HOA and other published work.There are plenty of optimization methods to solve this problem in the literature,such as coevolutionary PSO(CPSO)[47],hybrid PSO(HPSO)[48],coevolutionary DE(CDE)[49],FA[50],GA[51],cultural algorithms with evolutionary programming(CAEP)[52],water cycle algorithm(WCA)[53],ABC[54],MBA[46],ISA[24],and improved global-best-guided PSO(IGPSO)[55].The statistical results using the abovementioned optimizers and HOA are shown in Table 13.As we can observe from Table 13,in terms of the best solution and the number of function evaluations,HOA apparently outperforms the published methods.The best total cost is 1.724 852 308 597 365,with 100 000 FEs obtained by HOA.In addition,the mean value of HOA is the best,and its SD is better than those of the other algorithms,except for MBA,which means that our HOA is quite competitive with the other compared methods.
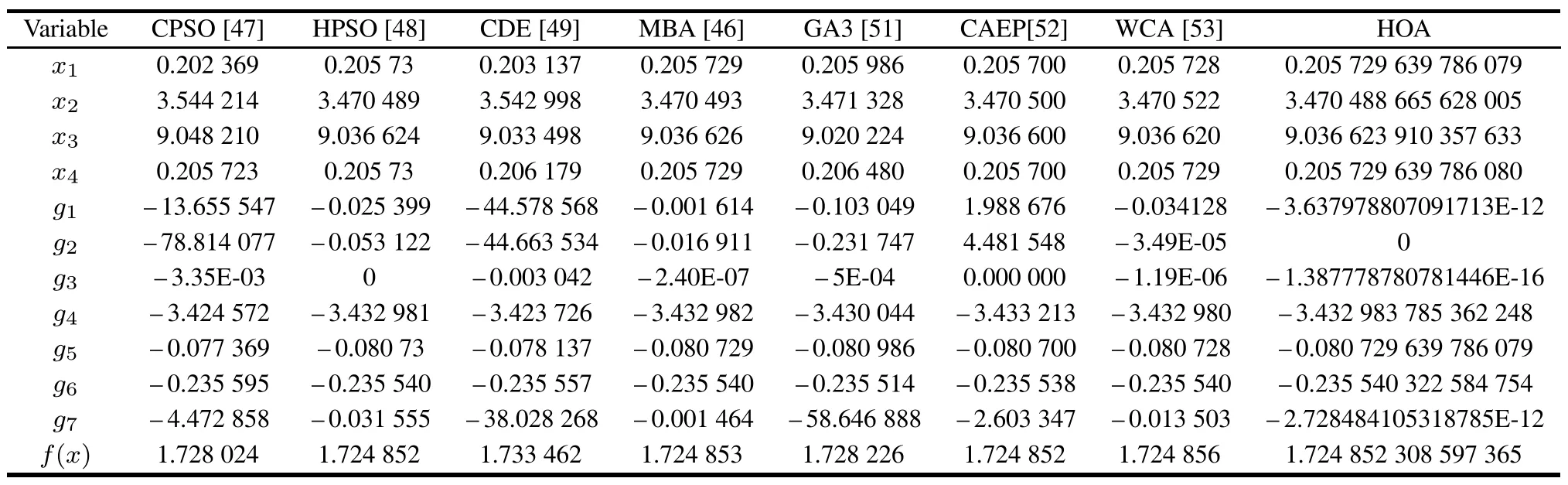
Table 12 Comparison of the best solution found by previous works for the welded beam design problem

Table 13 Comparison of statistical results found by different works for the welded beam design problem
4.Conclusions
With the development of society,studying new optimizationalgorithms for solving complex optimization problems has become a research hots pot.Based on the search behavior of hummingbirds during the foraging process,this paper proposes an HOA.The proposed algorithm can be divided into two phases:the self-searching phase and the guide-searching phase.The self-searching phase mainly simulates the cognitive behavior of hummingbirds.On the one hand,HOA uses gradient information for targeted searching to improve search efficiency.On the other hand,it uses Levy flight for random searching to jump out of local optima.The guide-searching phase mimics the territorial behavior of hummingbirds.In this phase,HOA uses the optimal and random individuals as guiding information,which effectively balances the exploitation and exploration abilities.Through the collaborative operation of these two search phases,the final solution is obtained.
For experiment study,ten classic benchmark functions are selected to test the performance of HOA.The results prove that HOA outperforms other classic and state-of the-art algorithms.Moreover,two engineering design optimization problems,the three-bar truss design problem and the welded beam design problem,are used as constrained problems to evaluate the performance of HOA.The results demonstrate that HOA can achieve the best performance among many published algorithms.Therefore,our HOA will most likely become a new optimization tool and can replace the existing optimization methods.
Future work can be expanded in these areas:First,the binary and multi-objective versions of HOA are worth researching.Second,the HOA can be hybridized with other optimization algorithms to improve its performance.Finally,studying the application of HOA in fields such as image processing,inverse geophysical problems,eco-nomic statistical design,and petroleum production optimization is of practical significance.
[1]HOLLAND J.Genetic algorithms.Scientific American,1992,267(1):66–72.
[2]STORN R,PRICE K.Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces.Journal of Global Optimization,1997,11(4):341–359.
[3]FARASAT A,MENHAJ M B,MANSOURI T,et al.ARO:a new model-free optimization algorithm inspired from asexual reproduction.Applied Soft Computing,2010,10(4):1284–1292.
[4]LI W,WANG L,CAI X,et al.Species co-evolutionary algorithm:a novel evolutionary algorithm based on the ecology and environments for optimization.Neural Computing&Applications,2015:1–10.
[5]PAN J S,MENG Z,CHU S C,et al.Monkey king evolution:an enhanced ebb-tide- fish algorithm for global optimization and its application in vehicle navigation under wireless sensor network environment.Telecommunications Systems,2017,65(3):1–14.
[6]EBERHART R C,KENNEDY J.A new optimizer using particles swarm theory.Proc.of the 6th International Symposium on Micro Machine and Human Science,1995:39–43.
[7]YANG X S,DEB S.Cuckoo search via Lvy flights.Proc.of the World Congress on Nature&Biologically Inspired Computing,2009:210–214.
[8]YANG X S.Fire fl y algorithm,stochastic test functions and design optimization.International Journal of Bio-Inspired Computation,2010,2(2):78–84.
[9]YANG X S,GANDOMI A H.Bat algorithm:a novel approach for global engineering optimization.Engineering Computations,2012,29(5):464–483.
[10]MIRJALILI S,MIRJALILI S M,LEWIS A.Grey wolf optimizer.Advances in Engineering Software,2014,69(3):46–61.
[11]MIRJALILI S.Moth- fl ame optimization algorithm:a novel nature-inspired heuristic paradigm.Knowledge-Based Systems,2015,89:228–249.
[12]ASKARZADEH A.A novel metaheuristic method for solving constrained engineering optimization problems:crow search algorithm.Computers&Structures,2016,169:1–12.
[13]LI M,ZHAO H,WENG X,et al.Cognitive behavior optimization algorithm for solving optimization problems. Applied Soft Computing,2016,39(C):199–222.
[14]EBRAHIMI A,KHAMEHCHI E.Sperm whale algorithm:An effective metaheuristic algorithm for production optimization problems.Journal of Natural Gas Science&Engineering,2016,29:211–222.
[15]SAREMI S,MIRJALILI S,LEWIS A.Grasshopper optimization algorithm:theory and application.Advances in Engineering Software,2017,105:30–47.
[16]MOOSAVI S H S,BARDSIRI V K.Satin bowerbird optimizer:a new optimization algorithm to optimize ANFIS for software development effort estimation.Engineering Applications of Artificial Intelligence,2017,60:1–15.
[17]RASHEDI E,NEZAMABADI-POUR H,SARYAZDI S.GSA:a gravitational search algorithm.Intelligent Information Management,2009,4(6):390–395.
[18]SHAH-HOSSEINI H.Principal components analysis by the galaxy-based search algorithm:a novel metaheuristic for continuous optimization.International Journal of Computational Science and Engineering,2011,6:132–140.
[19]MOEIN S,LOGESWARANR.KGMO:a swarm optimization algorithm based on the kinetic energy of gas molecules.Information Sciences,2014,275(3):127–144.
[20]KAVEH A,BAKHSHPOORI T.Water evaporation optimization:a novel physically inspired optimization algorithm.Computers&Structures,2016,167:69–85.
[21]TABARI A,AHMAD A.A new optimization method:electrose arch algorithm.Computers&Chemical Engineering,2017,103:1–11.
[22]RAO R V,SAVSANI V J,VAKHARIA D P.Teaching learning-based optimization:an optimization method for continuous non-linear large scale problems.Information Sciences,2012,183(1):1–15.
[23]ZONG W G,KIM J H,LOGANATHAN G V.A new heuristic optimization algorithm:harmony search.Simulation Transactions of the Society for Modeling&Simulation International,2001,76(2):60–68.
[24]GANDOMI A H.Interior search algorithm(ISA):a novel approach for global optimization.ISA Transactions,2014,53(4):1168–1183.
[25]AHMADI S A.Human behavior-based optimization:a novel metaheuristic approach to solve complex optimization problems.Neural Computing&Applications,2016:1–12.
[26]MOUSAVIRAD S J,EBRAHIMPOUR-KOMLEH H.Human mental search:a new population-based metaheuristic optimization algorithm.Applied Intelligence,2017,3:1–38.
[27]WOLPERT D H,MACREADY W G.No free lunch theorems for optimization.IEEE Trans.on Evolutionary Computation,1997,1(1):67–82.
[28]CLARK C J,DUDLEY R.Flight costs of long,sexually selected tails in hummingbirds.Proceedings Biological Sciences,2009,276(1664):2109.
[29]HEALY S D,HURLY T A.Cognitive ecology:foraging in hummingbirds as a model system.Advances in the Study of Behavior,2003,32(3):325–359.
[31]EWALD P W,BRANSFIELD R J.Territory quality and territorial behavior in two sympatric species of hummingbirds.Behavioral Ecology&Sociobiology,1987,20(4):285–293.
[33]PAVLYUKEVICH I.Lvy flights,non-local search and simulated annealing.Journal of Computational Physics,2007,226(2):1830–1844.
[34]MANTEGNA R N.Fast,accurate algorithm for numerical simulation of Lvy stable stochastic processes.Physical Review E:Statistical Physics Plasmas Fluids&Related Interdisciplinary Topics,1994,49(5):4677–4683.
[35]LI M,ZHAO H,WENG X,et al.Artificial bee colony algorithm with comprehensive search mechanism for numerical optimization.Journal of Systems Engineering and Electronics,2015,26(3):603–617.
[36]SHI Y,EBERHART R.A modified particle swarm optimizer.Proc.of the IEEE International Conference on Evolutionary Computation,1998:69–73.
[37]LI L X,SHAO Z J,QIAN J X.An optimizing method based on autonomous animals: fish-swarm algorithm.Systems Engineering—Theory&Practice,2002,22(11):32–38.
[38]KARABOGAD,BASTURKB.Apowerful and efficient algo-rithm for numerical function optimization:artificial bee colony(ABC)algorithm.Journal of Global Optimization,2007,39:459–471.
[39]MIRJALILI S.SCA:a sine cosine algorithm for solving optimization problems.Knowledge-Based Systems,2016,96:120–133.
[40]DERRAC J,GARC´IA S,MOLINA D,et al.A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms.Swarm&Evolutionary Computation,2011,1(1):3–18.
[41]RAY T,LIEW K M.Society and civilization:an optimization algorithm based on the simulation of social behavior.IEEE Trans.on Evolutionary Computation,2003,7(4):386–396.
[42]WANG Y,CAI Z,ZHOU Y,et al.Constrained optimization based on hybrid evolutionary algorithm and adaptive constraint-handling technique.Structural&Multidisciplinary Optimization,2009,37(4):395–413.
[43]ZHANG M,LUO W,WANG X.Differential evolution with dynamic stochastic selection for constrained optimization.Information Sciences,2008,178(15):3043–3074.
[44]LIN G H,ZHANG J,LIU Z H.Hybrid particle swarm optimization with differential evolution for numerical and engineering optimization.Applied Soft Computing,2010,10(2):1–12.
[45]GANDOMI A H,YANG X S,ALAVI A H.Erratum to:Cuckoo search algorithm:a metaheuristic approach to solve structural optimization problems.Engineering with Computers,2013,29(2):245–245.
[46]SADOLLAH A,BAHREININEJAD A,ESKANDAR H,et al.Mine blast algorithm:a new population based algorithm for solving constrained engineering optimization problems.Applied Soft Computing,2013,13(5):2592–2612.
[47]KROHLING R A,COELHO L D S.Coevolutionary particle swarm optimization using Gaussian distribution for solving constrained optimization problems.IEEE Trans.on Systems Man&Cybernetics Part B:Cybernetics,2006,36(6):1407.
[48]HE Q,WANG L.A hybrid particle swarm optimization with a feasibility-based rule for constrained optimization.Applied Mathematics&Computation,2007,186(2):1407–1422.
[49]HUANG F,WANG L,HE Q.An effective co-evolutionary differential evolution for constrained optimization.Applied Mathematics&Computation,2007,186(1):340–356.
[50]GANDOMI A H,YANG X S,ALAVI A H.Mixed variable structural optimization using fire fl y algorithm.Computers&Structures,2011,89(23/24):2325–2336.
[51]COELLO C A C.Use of a self-adaptive penalty approach for engineering optimization problems.Computers in Industry,2000,41(2):113–127.
[52]COELLO C A C,BECERRA R L.Efficient evolutionary optimization through the use of a cultural algorithm.Engineering Optimization,2004,36(2):219–236.
[53]ESKANDAR H,SADOLLAH A,BAHREININEJAD A,et al.Water cycle algorithm—a novel metaheuristic optimization method for solving constrained engineering optimization problems.Computers&Structures,2012,110/111(10):151–166.
[54]AKAY B,KARABOGA D.Arti fi cial bee colony algorithm for large-scale problems and engineering design optimization.Journal of Intelligent Manufacturing,2012,23(4):1001–1014.
[55]OUYANG H B,GAO L Q,LI S,et al.Improved global-bestguided particle swarm optimization with learning operation for global optimization problems.Applied Soft Computing,2017,52(C):987–1008.
 Journal of Systems Engineering and Electronics2018年2期
Journal of Systems Engineering and Electronics2018年2期
- Journal of Systems Engineering and Electronics的其它文章
- Health evaluation method for degrading systems subject to dependent competing risks
- Remaining useful life prediction for a nonlinear multi-degradation system with public noise
- Multi-focus image fusion based on block matching in 3D transform domain
- Hybrid artificial bee colony algorithm with variable neighborhood search and memory mechanism
- Direction navigability analysis of geomagnetic field based on Gabor filter
- Integrated modeling of spacecraft relative motion dynamics using dual quaternion
