Remaining useful life prediction for a nonlinear multi-degradation system with public noise
ZHANG Hanwen,CHEN Maoyin,and ZHOU Donghua,2,*
1.Department of Automation,Tsinghua University,Beijing 100084,China;2.College of Electrical Engineering and Automation,Shandong University of Science and Technology,Qingdao 266590,China
1.Introduction
Prognostics and health management(PHM)has been widely studied during the last several decades.Accurate remaining useful life(RUL)prediction results can provide effective basis for formulating maintenance schedules,and then increase systems’reliability and decrease their risk[1].As a consequence,RUL prediction has been considered as acrucial procedure in PHM[2,3],which is generally defined as the probability density function(PDF)of the first hitting time(FHT)[4,5].
From the existing literature,data driven RUL prediction approaches are usually divided into two classes:failure time data based approaches[6,7]and performance degradation data based approaches[8,9].Note that,for most practical equipment,the performance degradation data are easier to be achieved than the failure time data.In addition,the performance degradation data can reveal the detailed degradation mechanism of a specific system.Therefore,the performance degradation data based approaches are more desired and credible than failure time data based approaches.Many efforts have been made to achieve effective RUL prediction by degradation modeling.Some typical degradation models based on the Wiener process,the Gamma process or random coefficient regression(RCR)are proposed.However,most of the reported methods neglect the interdependency between degradations or only consider one degradation[10–12].In our previous work,an RUL prediction method for multi-degradation systems with public noise has been proposed[13].However,this method is based on an assumption that all the degradations are linear.In addition,the RUL of the whole system is not given.
However,in practical industry processes,equipment is generally composed by several parts or components,and there may exist correlations among the degradations of the system.Therefore,neglecting the correlations among degradations will result in inefficient prediction.Therefore,the correlations among degradations should be taken into account.As all the parts or components of a system work in the same circumstance and affect each other,there must exist public elements in their degradations.In this paper,the noise which impacts every degradation of the system is called the public noise.Here our main interest is to estimate the RUL of each single degradation and the whole system,respectively.
This paper is structured as follows.Section 2 introduces a nonlinear multi-degradation model.An estimation method is presented in Section 3 to estimate the degradation states as well as unknown parameters in the degradation model.In Section 4,we derive the PDF of FHT for each degradation and the whole system.In Section 5,a practical case is provided to prove the proposed method.Finally,conclusions of this paper are given in Section 6.
2.Multi-degradation model
To predict the RUL for a class of nonlinear multi-degradation systems, a method is presented. In the real industrial processes, systems are usually composed by several parts or components,and these parts or components are working in the same environment,thus the degradations of these parts or components will be influenced by common factors.To describe such a phenomenon in degradations,a multi-degradation model with public noise is proposed.To identify the degradation states and the unknown parameters,an iterative estimation method is proposed by using the Kalman filter and the expectation maximization(EM)algorithm.Next,with known thresholds,the RUL of each degradation can be predicted by using the FHT.In addition,the RUL of the whole system can be obtained by a Copula function.Finally,a practical case is used to demonstrate the proposed method.To characterize the degradation of a multi-degradation system influenced by public noise,we establish a nonlinear multidegradation model by adding a public Brownian motion to the traditional Wiener process with nonlinear drift. In order to obtain the RUL prediction, the multi-degradation system needs to satisfy the following assumptions:
(i)The system includesmdegradations,and each dgradation can be observed by a sensor.
(ii)The degradations of the system are observed by the same kind of sensors.
(iii)The failure mode of the system is competing failure,i.e.,it is regarded as the failure of the system,once any degradation of the system exceeds the threshold.
(iv)The threshold of the each degradation is known.
Then the multi-degradation can be described by anmdimension vectorY(t)=[Y(1)(t),Y(2)(t),···,Y(m)(t)]T.Each degradation can be denoted by a Wiener process with a nonlinear drift and two independent Brownian motions,which is formulated by

whereis the initial value of theith degradationY(i)(t),i=1,2,...,m,ψ(i)(t;Θ)denotes the drift coefficient of theith degradation,Θis a set of the unknown parameters inψ(i)(t;Θ),λ(i)andγ(i)are diffusion coefficients.B(t)andB(i)(t)are standard Brownian motions,whereB(t)characterizes the public noise which influences all the degradations,andB(i)(t)is distinct from each other in each degradation because it characterizes the private noises.Without loss of generality,here we assume
As themdegradations are observed bymsensors,we can formulate the measurement equation as follows:

To describe different degradation paths of various equipment,the drift coefficientψ(i)(t;Θ)can be any form.To obtain a closed-form expression of RUL,we only require thatψ(i)(t;Θ)is continuous with respect tot.To embody the degradation,we use three different forms ofψ(i)(t;Θ).
The corresponding degradation processes can be denoted as

3.Identification of the degradation model
In order to estimate the RUL of the multi-degradation system,the degradation states and the parameters in themdegradation model should be estimated firstly.ForM1,we haveWhile,forM2andWe propose the joint estimation ofykandΘby combining the Kalman filter with the EM algorithm in this section.
3.1 Estimation of degradation states
Firstly,we use a Kalman filter[14]to estimateykaccording to the measurement vectorzk.
(i)Time-update:According to the last estimation,update the one-step predictions and variances by

3.2 Estimation of parameters
Note that the EM algorithm[15]can identify parameters by using incomplete or missing data.In order to identify the unknown parameters online with estimated degradation states,we propose a recursive identify method in this section.For simplicity,we defineand,forM1,M2andM3,respectively.Based on the estimated degradation states obtained by(10)–(14),the EM estimation in thelth iterative step can be given by

(ii)M-step:Calculate the estimates by maximizing

Owing to the nonlinear drift coefficient,the analytical solutions of the estimates are intractable to deduce by making the partial derivatives equal to zero.Here we use their numerical solutions obtained by the Matlab function“fminsearch”.
4.RUL prediction
4.1 RUL of a single component
The RUL of each part or component is very informational for scheduling maintenance actions.The RUL is usually defined as the time interval from the present timetkto the failure timeTf,namely,

The RUL attkof theith degradation with a known thresholdη(i)can be formulated as
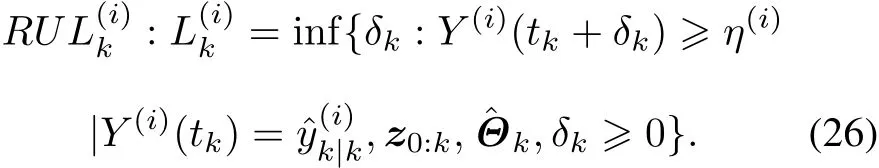
It can be easily proved that the sum of two independent Brownian motions is also a Brownian motion.Therefore,for a single degradation,we use a Brownian motionB′(i)(t)to replaceB(i)(t)andB(t).Setδk=t-tk,then theith degradation can be expressed by(27)at the sampling timetkgivent≥tk.
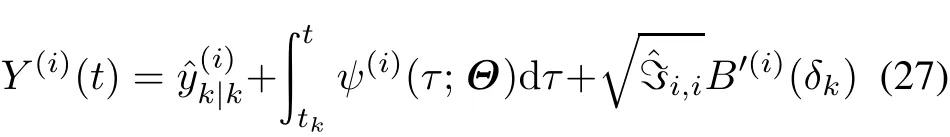
To achieve the analytical form of RUL of each degradation,we use Lemma 1 to calculate the FHT of the stochastic process given by(27).
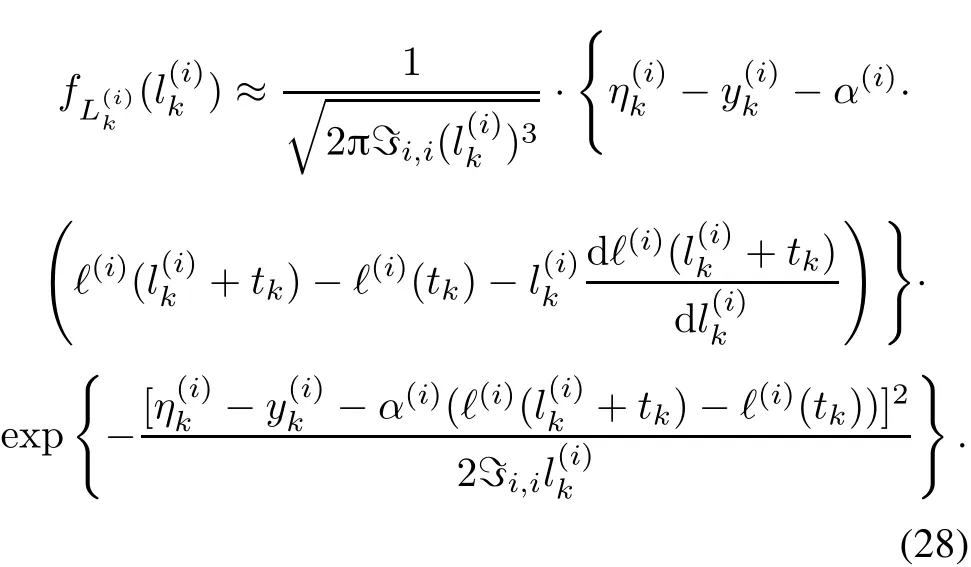
Lemma 1[17] For degradation(27),ifψ(i)(t;Θ)is continuous with respect tot,the PDF of RUL with the thresholdη(i)can be approximated as According to Lemma 1,we can deduce the RULs for the specific degradations expressed byM1,M2andM3.The main results are provided in Corollary 1.
Corollary1For degradation processes(7),(8)and(9),the PDF of RUL with a thresholdη(i)can be given as
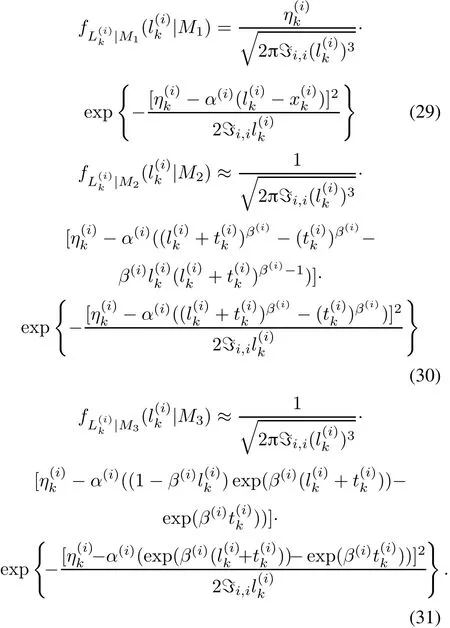
4.2 RUL of the whole system
From Corollary 1,the RUL of each single degradation can be obtained.To predict the RUL of the whole system,we use a Copula function to combine the marginal distribution of each degradation.Firstly,we calculate the cumulative distribution function(CDF)of RUL of each degradation by

The Copula function is a method of correlation analysis and multiple statistical analysis,which can obtain the joint distribution by combining several one-dimensional marginal distributions[18].The existence of the Copula function can be illustrated by the Sklar theorem.
Lemma 2(Sklar theorem)[19]Any multivariate joint distribution can be written by univariate marginal distribution functions with a Copula function,which describes the dependence between the variables.
Here we suppose that the failure mode of the system is the competing failure.Therefore,we can define the RUL of the whole system as

Then by the Copula function,we can obtain the distribution of RUL of the whole systemFLk(lk)as follows:

whereC(·)is a Copula function,andθis a matrix of parameters.Here,the maximum likelihood estimation(MLE)method is adopted to identifyθ.The likelihood function is given by
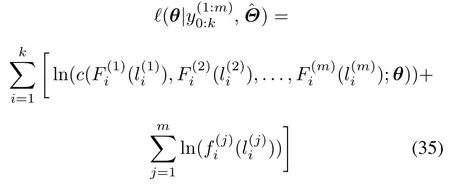
wherec(·)is the PDF ofC(·).Then the estimation ofθcan be obtained by maximizing
To obtain the RUL of the whole system,the Gaussian Copula function is adopted here.With the CDF of RUL of each degradation obtained by (32) and the estimated matrixθ,the CDF of RUL of the whole system can be formulated by
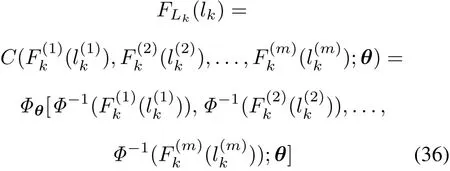
whereΦθis anm-dimensional normal distribution with correlation matrixθ.The PDF of RUL of the whole system can be deduced by taking the derivative ofFLk(lk).
5.Case study
To demonstrate the proposed method,an actual example of a blast furnace wall is adopted.The degradation d at a are collected from a blast furnace with a capacity of 1 000 m2in Jiayuguan,China.The degradations of three positions of the blast furnace wall are collected.Since the temperature of the blast furnace wall can reflect the residual thickness,we use the temperature as the degradation to predict the RUL.The three degradations are shown in Fig.1.The degradation 1 is observed by a temperature sensor located with a height of 7.395 m and a depth of 0.15 m northeast,the degradation 2 is observed by a temperature sensor located with a height of 8.936 m and a depth of 0.4 m southwest,and the degradation 3 is observed by a temperature sensor located with a height of 10.139 m and a depth of 0.15 m northwest.
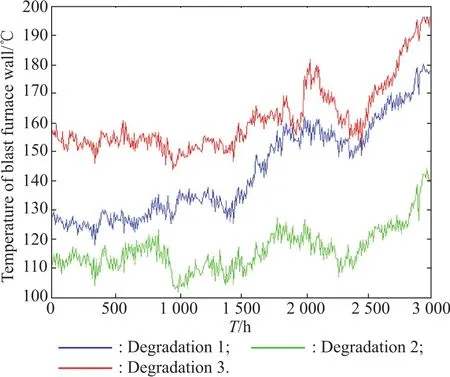
Fig.1 Degradations of the three positions of a blast furnace wall
As the operation and the fluctuation of the furnace condition affect the whole blast,there may exist public noise in the degradations of different parts of the blast furnace wall.From Fig.1,we find that the three degradations have a common trend to some extent,even though they are located in different directions and deepness.To demonstrate the common trend among the three degradations,the co-integration test is employed[20,21].From the pairwise tests of the degradations,the common trend can be found between degradation 1 and degradation 2 with 96.38%confidence,between degradation 1 and degradation 3 with 86.26%confidence,and between degradation2 and degradation 3 with 99.80%confidence.Thus the proposed degradation model is more suitable for the degradations.Next,we compare our method with a traditional method[10]neglecting the public noise.
According to the presented method,a degradation model with public noise for the three degradations can be established.Here we useM2to establish the degradation model.Then the unknown parameters can be identified by the approach presented in Section 3.Main estimations are listed in Table 1.

Table 1 Estimations of main parameters
To avoid casualties caused by burning through,blast furnaces are usually stopped in a conservative manner.Thus the total life cycle data of blast furnace walls are hard to acquire.Here we only consider the FHT of the degradation passing a set threshold.The thresholds are supposed to be 175°for degradation 1,130°for degradation 2,and 190°for degradation 3.Then,the failure time of the three degradations is the 2 848th hour,the 2 784th hour and the 2 776th hour,respectively.According to Corollary 1,we obtain the RULs of the degradations(as shown in Fig.2).To verify the superiority of the presented method,we also obtain the RUL predictions by a traditional method[10]which neglects the public noise (as shown in Fig. 2).Moreover,to quantify the performance of the methods,the mean square error(MSE)is employed(as shown in Table 2).Note that,it means the failure of the whole blast furnace,if any point of the blast furnace wall burns through,i.e.the failure mode of the blast furnace is competing failure.We simply assume that the RUL of the blast furnace wall is determined by the three degradations.Therefore,the failure time is the 2 776th hour.

Table 2 MSEs of the RUL predictions

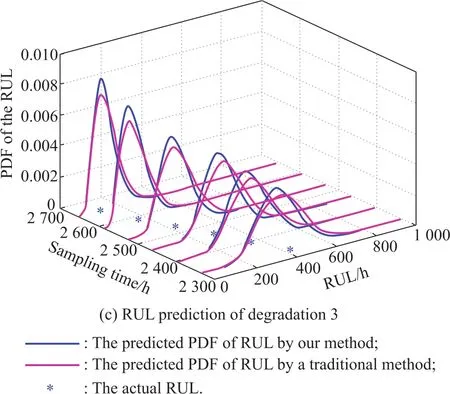
Fig.2 RUL prediction of each single degradation
Fig.3 shows the RULs of the blast furnace wall obtained by the Copula function with results achieved by the proposed method and the traditional method,respectively.And the MSEs of the whole system’s RUL predictions obtained by the two methods are also listed in Table 2.
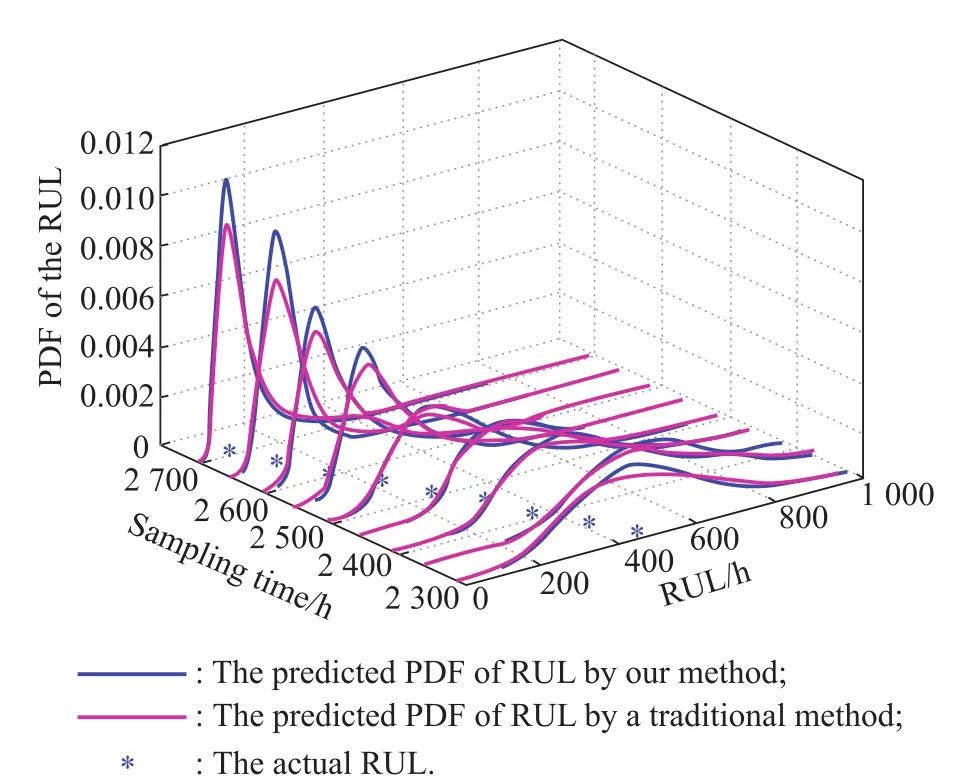
Fig.3 Combined RUL prediction with the three degradations
The results given by Fig.2,Fig.3 and Table 2 demonstrate that the proposed RUL prediction method for single degradation and the whole system works well and efficiently for the degradations of the blast furnace wall,compared with the traditional method which neglects the public noise.
6.Conclusions
In order to predict the RULs of a kind of multi-degradation systems affected by the public noise,a nonlinear multidegradation model is proposed.To characterize the public noise,a public Brownian motion is formulated in each degradation process.In addition,the measurement noise is also taken into account.To identify the degradation states and unknown parameters,a joint online identification algorithm is presented.Then the RUL of each degradation is obtained in the sense of FHT.The RUL of the whole system is also obtained by a Copula function.A case study of a blast furnace wall is presented to demonstrate the validity of the presented method.
[1]PECHT M.Prognostics and health management of electronics.Hoboken:John Wiley&Sons,2008.
[2]BARALDI P,MANGILI F,ZIO E.Investigation of uncertainty treatment capability of model-based and data-driven prognostic methods using simulated data.Reliability Engineering&System Safety,2013,112(2):94–108.
[3]SI X S,HU CH,KONGX,et al.Aresidual storage life prediction approach for systems with operation state switches.IEEE Trans.on Industrial Electronics,2014,61(11):6304–6315.
[4]JARDINE A K S,LIN D,BANJEVIC D.A review on machinery diagnostics and prognostics implementing condition based maintenance.Mechanical Systems and Signal Processing,2006,20(6):1483–1510.
[5]ZHANG H,CHEN M,XI X,et al.Remaining useful life prediction for degradation processes with long-range dependence.IEEE Trans.on Reliability,2017,66(4):1368–1379.
[6]KALBFLEISCH J D,PRENTICE R L.The statistical analysis of failure time data.Hoboken:John Wiley&Sons,2011.
[7]MEEKER W Q,ESCOBAR L A.Statistical methods for reliability data.Hoboken:John Wiley&Sons,2014.
[8]LEE J,WU F,ZHAO W,et al.Prognostics and health management design for rotary machinery systems–reviews,methodology and applications.Mechanical Systems and Signal Processing,2014,42(1):314–334.
[9]SI X S,WANG W,HU C H,et al.Remaining useful life estimation:a review on the statistical data driven approaches.European Journal of Operational Research,2011,213(1):1–14.
[10]WANG X,GUO B,CHENG Z.Residual life estimation based on bivariate Wiener degradation process with time-scale transformations.Journal of Statistical Computation and Simulation,2014,84(3):545–563.
[11]WANG H K,LI Y F,HUANG H Z,et al.Near-extreme system condition and near-extreme remaining useful time for a group of products.Reliability Engineering&System Safety,2017,162:103–110.
[12]RODRIGUES L.Remaining use full ife prediction for multiple-component systems based on a system-level performance indicator.IEEE/ASME Trans.on Mechatronics,2018,23(1):141–150.
[13]ZHANG H,CHEN M,ZHOU D.Predicting remaining useful life for a multi-component system with public noise.Proc.of the Prognostics and System Health Management Conference,2016:1–6.
[14]KALMAN R E.A new approach to linear filtering and prediction problems.Journal of Basic Engineering,1960,82(1):35–45.
[15]DEMPSTER A P,LAIRD N M,RUBIN D B.Maximum likelihood from incomplete data via the EM algorithm.Journal of the Royal Statistical Society-Series B(Methodological),1977,39(1):1–38.
[16]DEWAR M,KADIRKAMANATHAN V.A canonical space time state space model:state and parameter estimation.IEEE Trans.on Signal Processing,2007,55(10):4862–4870.
[17]SI X S,WANG W,HU C H,et al.Remaining useful life estimation based on a nonlinear diffusion degradation process.IEEE Trans.on Reliability,2012,61(1):50–67.
[18]NELSEN R B.An introduction to copulas.New York:Springer Science&Business Media,2007.
[19]SKLAR A.Random variables,joint distribution functions,and copulas.Kybernetika,1973,9(6):449–460.
[20]AHMAD J,HARNHIRUN S.Cointegration and causality between exports and economic growth:evidence from the ASEAN countries.The Canadian Journal of Economics/Revue canadienne d’Economique,1996,29(s1):413 – 416.
[21]ENGLE R F,GRANGER C W J.Co-integration and error correction:representation,estimation,and testing.Econometrica:Journal of the Econometric Society,1987,55(2):251–276.
 Journal of Systems Engineering and Electronics2018年2期
Journal of Systems Engineering and Electronics2018年2期
- Journal of Systems Engineering and Electronics的其它文章
- Health evaluation method for degrading systems subject to dependent competing risks
- Multi-focus image fusion based on block matching in 3D transform domain
- Hybrid artificial bee colony algorithm with variable neighborhood search and memory mechanism
- An optimization method:hummingbirds optimization algorithm
- Direction navigability analysis of geomagnetic field based on Gabor filter
- Integrated modeling of spacecraft relative motion dynamics using dual quaternion
