Integrated modeling of spacecraft relative motion dynamics using dual quaternion

PENG Xuan,SHI Xiaoping,and GONG Yupeng

1.Control and Simulation Center,Harbin Institute of Technology,Harbin 150080,China;2.Research Center of Satellite Technology,Harbin Institute of Technology,Harbin 150080,China

1.Introduction

With rapid development of aerospace technology,new space missions,like space rendezvous and docking(RVD),satellite formation flying(SFF),on-orbit maintenance and so on,have proposed higher requirements for control accuracy of relative position and attitude.To complete these tasks,an accurate model of 6 degree-of-freedom(6-DOF)relative motion must be established.For simplicity,traditionally,position and attitude are separately modeled and controlled,without considering their coupling.However,to realize high accurate control of relative position and attitude,their coupling must be deeply explored.

Recently,there are mainly two ways in research of position and attitude coupling.One is‘independent-coupled’modeling.First separately model the relative position and attitude motion.Then the coupling terms are artificially introduced and finally the coupled dynamics is built.In[1–10],the coupling is mainly reflected in the impact of attitude error on position.However,this modeling method can hardly include all coupling terms.What’s worse,most of them do not have clear physical meaning or formation causes.

The other way is building an integrated model using dual quaternion.The Charles theory shows that the general motion of any space rigid body can be realized by the rotation around one axis and the translation along this axis.This combination of rotation and translation is called screw motion,which is often used to describe the general motion of the space rigid body[11].To describe the screw motion,dual quaternion has proved to be the most efficient and compact method with the least computation[12].Dual quaternion has already been successfully applied in space robot[13,14],mechanism kinematics[15,16],inertial navigation[17,18]and so on.

However,in close on-orbit service,there are not much application.Due to the novelty and special operation rules of dual quaternion,using it to build the integrated dynamics model of relative motion is very difficult.In[19–25],the integrated models of relative motion based on dual quaternion either are too complicated to understand or have no clear modeling process.Until now,there is no unified model of relative motion based on dual quaternion,which also hinders the consequent deeper research.

2.Mathematical foundation

2.1 Quaternion

Quaternion is the extension of the complex number in four dimensional(4D)real space R4,which is defined as

If the scalar partqsis 0,the quaternion is called vector quaternion,which is equal to a vector.If the vector partqvis 0,the quaternion is called scalar quaternion,which is equal to a scalar.Thus vector and scalar quaternion can inter convert with the normal vector and scalar according to specific computation requirements.

Based on the Euler finite rotation theory,supposing coordinateArotates angleΦaround axiseand becomes coordinateB,then this rotating coordinate transform can be described by quaternion which is defined by Euler parameters,as

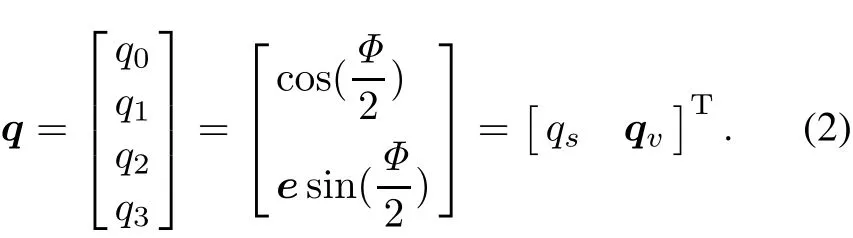
As(2)shows,when used to describe rotation, the quaternion’s four parameters are not independent,which satisfy the following constraint:

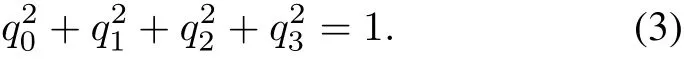
Quaternion which satisfies(3)is called unit quaternion.

The operation rules of quaternion used in this paper are given as follows,whereq,qaandqbare arbitrary quaternions.

Conjunction

Notice that the dot product returns a scalar,the cross product returns a 3D vector and the logarithm maps quaternion to 3D space.

In matrix form,quaternion multiplication can be expressed as

For three arbitrary quaternionsp,q,r,their multiplication satisfies

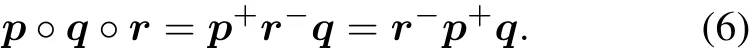
Suppose vectorris represented asin coordinateAand asin coordinateB.Then there is

If the corresponding direction cosine matrix isCba,then there is

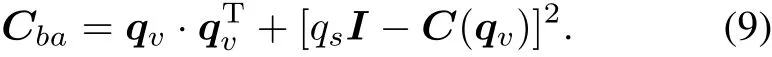
In the coordinate conversion of 3D vector or vector quaternion,using(9)to replace(7),which can make the dimension of this computation decrease from four to three.

2.2 Dual number and dual vector

In 1873,Clifford proposed the concept of dual number.Dual numberis defined as an ordered real number pair

whereaandbare respectively the real and dual parts of.εis the dual operator,which satisfiesε2=0 andThe dual number set is denoted by

In 1901,Study extended the concept of the dual number to space geometry to express the relationship between two lines,which is represented by dual angle

where the real partθand the dual partdrespectively represent the angle and distance between two lines,as Fig.1 shows.

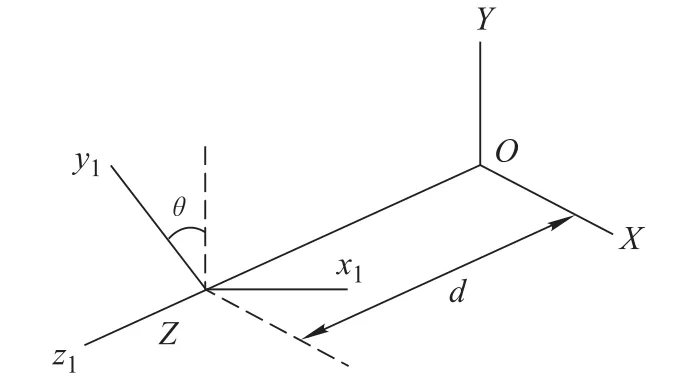
Fig.1 Dual angle

According to dual quaternion algebra,the dual function can be expanded into Taylor series.As for dual anglethere are

A dual vector is composed by three dual numbers,whose set is denoted by.The dualvector is of ten called motor and written as

Operation rules of the dual number and motor are similar to those of the real number and vector in linear algebra.Just bewareε2=0.

Definition 1IfaTb=0 andthe dual vector is called unit motor,which is denoted by

The geometric interpretation of the unit motor is showed in Fig.2.It represents space position of lineNrelative to originO.The real parta0is a unit vector parallel toNand the dual part describes lineN’s moment relative to originO,wherepis the position vector of the arbitrary point on lineN.

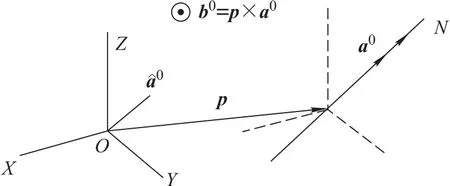
Fig.2 Unit motor

2.3 Dual quaternion

Dual quaternion can be defined as a dual number whose parameters are all quaternion

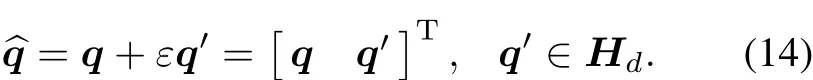
Also it can be defined as a quaternion whose parameters are all dual number

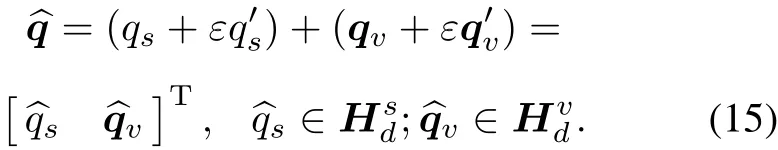
The dual quaternion set is denoted byHd.In computation,it is often expressed in form of an 8D vector.

The operation rules of dual quaternion are similar to those of quaternion,dual numbers and dual vectors.Just bewareε2=0.For simplicity,only some important rules are given as follows.

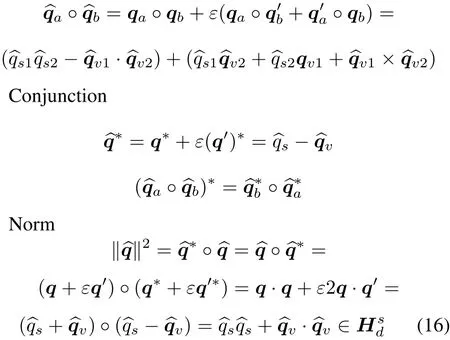
Multiplication Ifis called unit dual quaternion,which satisfies

Similar to quaternion,multiplication of dual quaternion can be expressed in matrix form as

As for arbitrary three dual quaternions,their multiplication satisfies

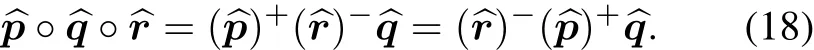
As Fig.3 shows,describe the screw motion of the space rigid body by the motion of the coordinate.CoordinateAfirstly rotatesΦaround screw axis,then shiftsdalongand finally becomes coordinateB.

Fig.3 Coordinates transform in dual quaternion

According to geometric meaning,this screw motion can be expressed by dual quaternion which is defined as

Compared with(2),we can see that dual quaternion and quaternion have the similar form when defined by geometric meaning.And there is

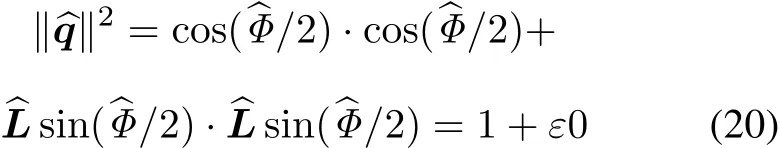
Dual quaternion which describes screw motion can also be interpreted as:coordinateAfirstly rotatesqand then shiftsrb.

When defined by(21),the real partqand dual partq′satisfy

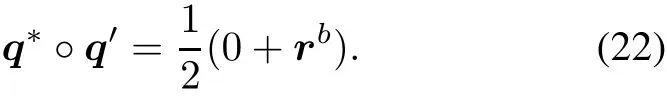
The real part of(22)is 0.Thus according to the rule of quaternion multiplication,there is

Notice thatqis a quaternion describing rotation,so there is

Equations(23)and(24)are two restraints of dual quaternion which is used to describe screw motion.They make the 8D space composed by dual quaternion decrease to a 6D space,and there is

As(20)and(25)show,no matter defined by either form,quaternion describing screw motion is always a unit quaternion.

If the dual vector is expressed asin coordinateAand asin coordinateB,then there is

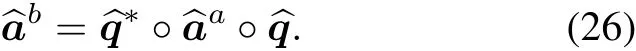
Besides,as for dual quaternion defined by(21),its logarithm is given as

Noting that the logarithm maps dual quaternion to a 6D vector.

By comparison of sections 2.1 and 2.3,it can be seen that,when describing motion,dual quaternion has many parallels with quaternion.In fact,according to the Kotelnikov transference principle,dual quaternion completely inherits properties of quaternion as shown in Table 1.

Table 1 Comparison of quaternion and dual quaternion

3.Coordinates

As shown in Fig.4,to establish the model of relative motion between the chaser and the target,some necessary coordinates are defined.

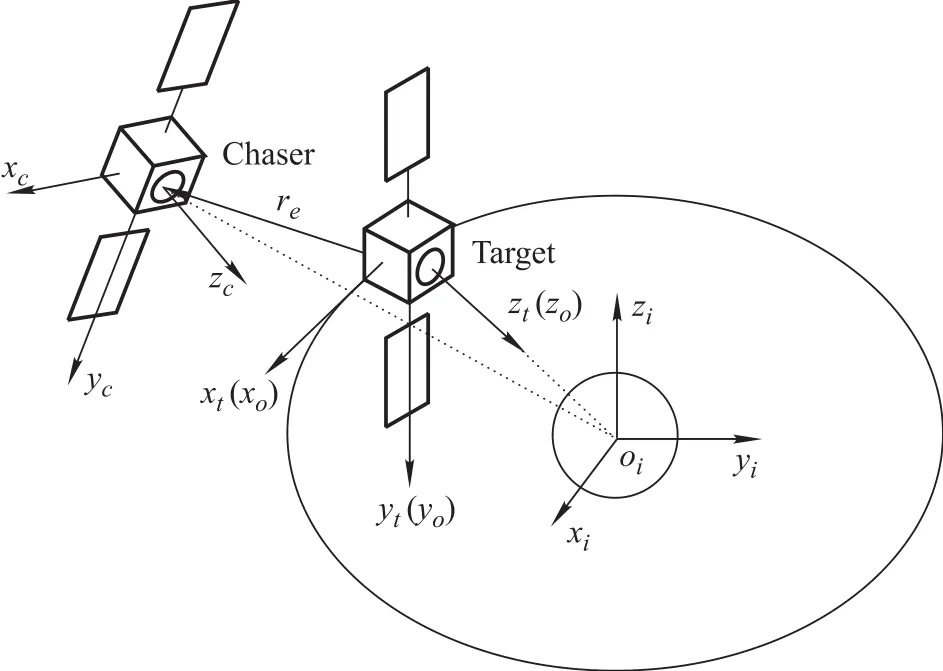
Fig.4 Coordinates

Earth centered inertial(ECI):denoted as frameI.It is a nonaccelerating reference frame with its origin in the center of the earth,xipointing to the vernal equinox,andzipointing to the north pole.yiis given by the right-hand rule.

Orbital coordinate:denoted as frameO.Its origin is at the centroid of spacecraft.zopoints from the origin to the earth center.xois vertical tozoin the orbital plane.yois parallel to the negative normal direction of the orbital plane.

Body fixed coordinate:denoted as frameB.It is centered at the centroid of spacecraft.Its three axes are parallel to three principal axes of inertia.When the spacecraft is at the state of the earth oriented attitude,frameBcoincides with frameO.The target’s body fixed coordinate is denoted as frameTand the chaser’s is denoted as frameC.

In the following sections,attitude,position,angular velocity and velocity all mean frameB’s motion relative to frameI.

4.Motion model based on dual quaternion

4.1 Integrated kinematics

Suppose the position vector and attitude quaternion of frameBarerandqrespectively.Then the spacecraft’s spatial position can be described by dual quaternion as

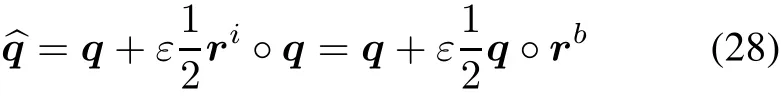
whereriandrbare respectively expressions ofrin frameIand frameB.Notice thatXarepresents expression ofXin frameA.

Take the derivative of(28).Then bring in the quaternion kinematic equation and use the cross product rule,we can get

Equation(29)is kinematic equation described by dual quaternion.Similarly,another form can be deduced as

Now we get the full description of integrated kinematic equation by dual quaternion as

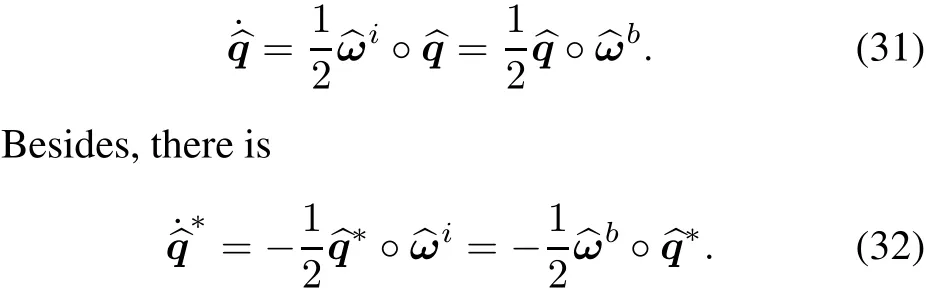
4.2 Time derivative of vector

Suppose coordinateArotates at

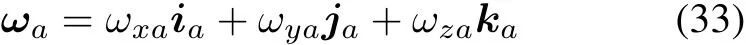
relative to inertial space.uis a changing vector.

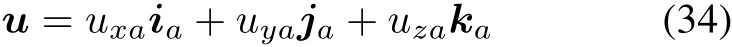
Then the time derivative ofuin inertial space can be written as

where dau/dtrepresents the time changerate ofurelative to the vector basenamely the relative derivative ofuin coordinateA.

In coordinateA,the component-wise form of(35)is

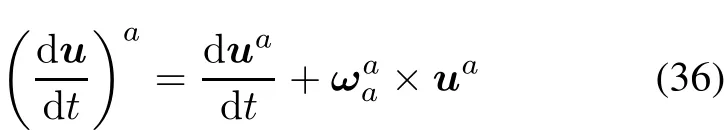
where(du/dt)ais the component vector of du/dtexpressed in coordinateA,dua/dtis the derivative of the component vector ofuexpressed inA,namely the relative derivative ofuin coordinateA.is coordinateA’s angular velocity expressed inA.

Extend this property to two changing coordinatesAandB,we can get

4.3 Integrated dynamics

If at one moment,a rigid body’s angle velocity isω,the velocity of arbitrary pointAon it isvA.Then its velocity motor can be described as

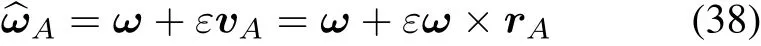
whereωis a sliding vector,which is not related to reference point andrAis the position vector ofA,sovAis a location vector which will change with the referencepoint.

Suppose at one moment,the force and the torque exerted on pointAarefAandMA.Apparently,the force is a sliding vector and the torque is a location vector.Thus the force motor can be expressed as

The rigid body’s momentum motor is

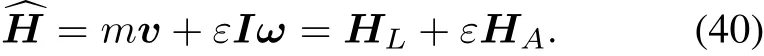
As shown in(40),linear momentumHLis a sliding vector whilevis a location vector,the angular momentum is a location vector while the angular velocityωis a sliding vector.We can see that when mass and moment of inertial are involved,the real part and dual part of velocity motor and momentum motor are exchanged.Thus we introduce operator d/dε,which has an opposite effect ofε,shown as

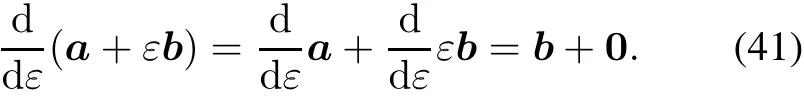
Then we introduce dual mass as

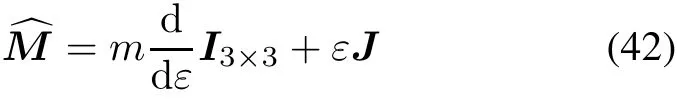
wheremis the mass of the rigid body,Jis the moment of inertia relative to the centroid.The inverse ofis defined as

Now,the spacecraft’s momentum motor relative to centroid can be rewritten as

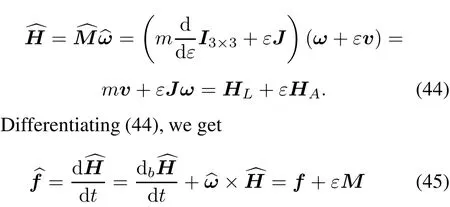
wherefandMare the net force and torque acted on the centroid of the spacecraft.

According to(36),rewritte(45)in frameBas follows:

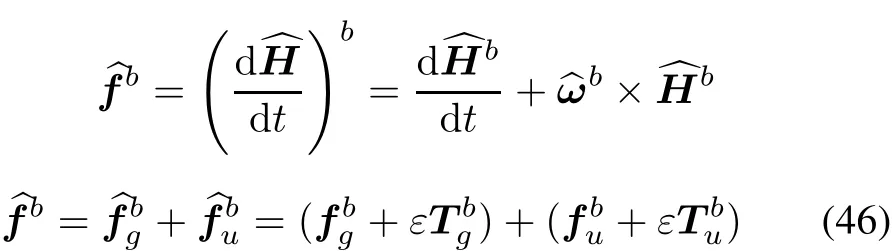
whereare respectively the gravity, gravity gradient torque, control force and control torque exerted on the spacecraft.

Equations(31)and(46)are the full integrated model of a single spacecraft’s position and attitude coupled motion.

5.Integrated modeling based on relative error

Error of relative motion is defined as the space position of frameCrelative to frameT.And the model based on relative error is established in frameC.

5.1 Relative kinematics

Suppose the target and chaser are in circular orbit,their spatial positions areThen their difference can be defined by multiplication as

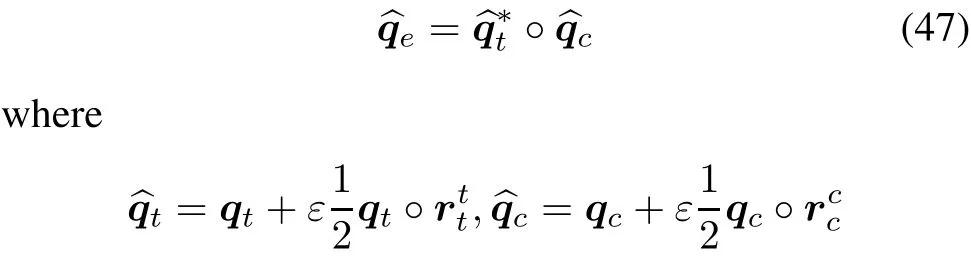
whereqtandqcare the target and chaser’s attitude quaternions.The spatial position error between two spacecrafts is

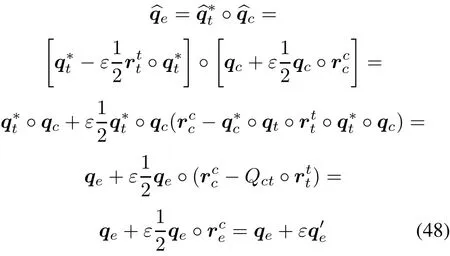
whereare rotational quaternion errors,is the translational quaternion error.We can see from(48)that the coupling between posit on and attitude has been integrated in the spatial position error described by dual quaternion.

In later sections,according to section 2.1,for coordinate transform of the 3D vector,replaceQctwithCct,which is calculated by(9).

Differentiating(48)and bringing in(31),we can get

This is the kinematic equation based on the error of relative motion.

5.2 Relative dynamics

Use the velocity motor error and target’s velocity motor to express the chaser’s velocity as

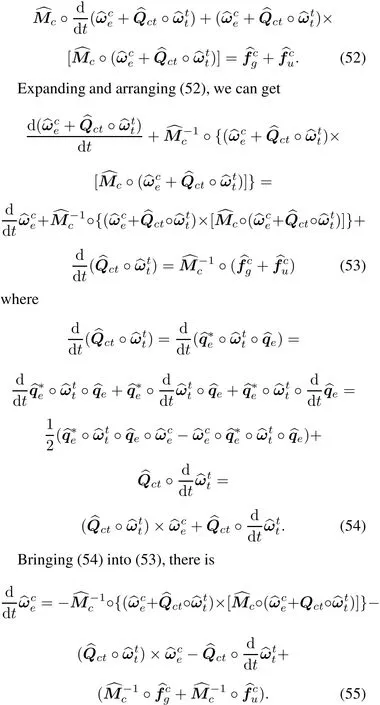
Equations(50)and(55)are kinematic and dynamic equations based on relative error.

Given the convenience of designing a controller,analyze the coupling effect,and decompose(50)and(55)into real and dual parts.Firstly,give the following definitions:

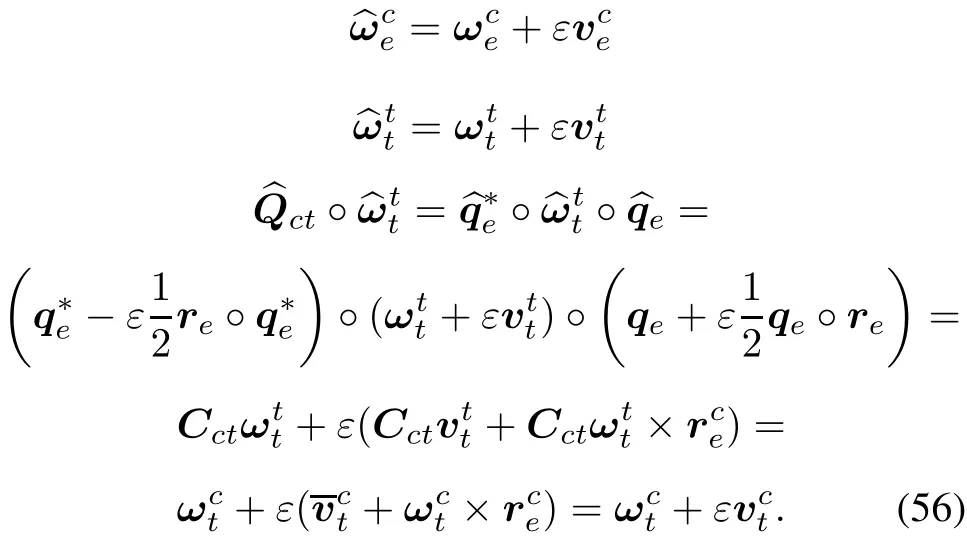
Based on these definitions,decomposition results of(50)can be directly given as

The decomposition of(55)is the difficulty and focus of the whole modeling process.Given the clarity and simplicity of derivation,the right four terms of(55)are decomposed separately as follows.

The first term:

Taking(58),(59),(61),(62)together and bringing in the definitions in(56),the real and dual parts of(59)can be written as

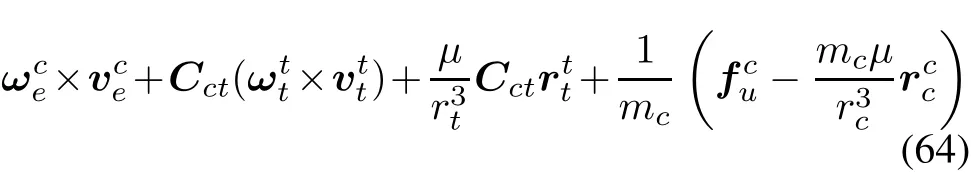
wherertandrcare the orbit radii of the target and the chaser,respectively.Given the distance between them can be neglected in comparison with the orbit radius,so we deem thatWe can see that attitude error parametersare involved in many terms in(64),which describes the translational motion.We can also see from(64)that the coupling between attitude and position is intricate.However,dual quaternion can describe the coupled relative motion in an integrated form,which is simple,compact and accurate as shown in(50)and(55),so we do not have to artificially add many complicated coupling terms.

5.3 Comparison with traditional coupled modeling method

In[3],relative position and attitude are separately modeled by different methods.And the coupling is divided in to coupled control inputs and coupled control instruction.Then relative position and attitude are artificially coupled via transformation between different coordinates. In[26],considering more coupling terms,the coupled model is much more complex than that in[3].

Based on the above analysis,this traditional modeling method has the following disadvantages.First,during the modeling process,detailed information of the target is needed,such as the target’s mass,moment of inertia,attitude quaternion and so on.As to non-cooperative targets, in practice, it is almost impossible to get so much information about the target,especially mass and moment of inertia.Second,to add the coupling terms,there are much coordinates transformations between ECI,body fixed frame and Hill frame,which are not only complicated but difficult to obtain accurate transformation relationships.Third,there is no unified and accurate model to describe the coupled relative motion.Because all coupling terms are added artificially,when using different modeling methods or considering different coupling factors,the final coupled models are all different,such as the model in[3],[4]and[26].

Using dual quaternion,these defects can be conquered at utmost.First,the coupled model can be built without much detailed information of the target like mass and moment of inertia.Second,coordinates transformation is only between two body fixed frames,which is easier and more feasible.Third, there is a unified and compact model to describe the coupled relative motion.

5.4 Coupled control

Dynamics described by(55)is strong coupled and nonlinear.Given the reliability and practicability,we adopt the generalized proportion-derivative(PD)control law.

5.4.1 Design of control law

The design object of the controller is to stabilize the close loop system described by(50)and(55).Namely0+ε0 and.For convenience,rewrite(55)as

Definition 2Supposingaandbare vectors of the same dimensions,define a new multiplication ‘.∗’as

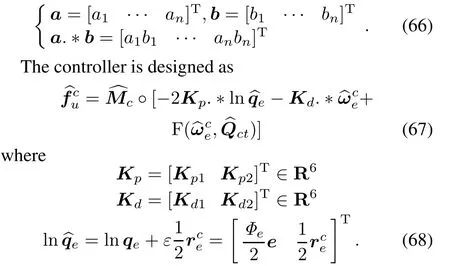
After decomposing(67)into real and dual parts,bring them into(63)and(64)respectively,then we can get

whereΦeandeare Euler parameters transferred fromqe.Based on the classic control theory,parameters of the generalized PD control law can be chosen as follows:

5.4.2 Simulation analysis

According to the former hypothesis,the velocity and angular velocity of the target can be described in frameTas

Other initial parameters are given in Table 2.represents the desired relative position.In order to be intuitive,initial errors of attitude angles and initial relative position are given instead of initial quaternions.The initial dual quaternion can be easily calculated based on the relation between attitude angle and quaternion,and by(48).

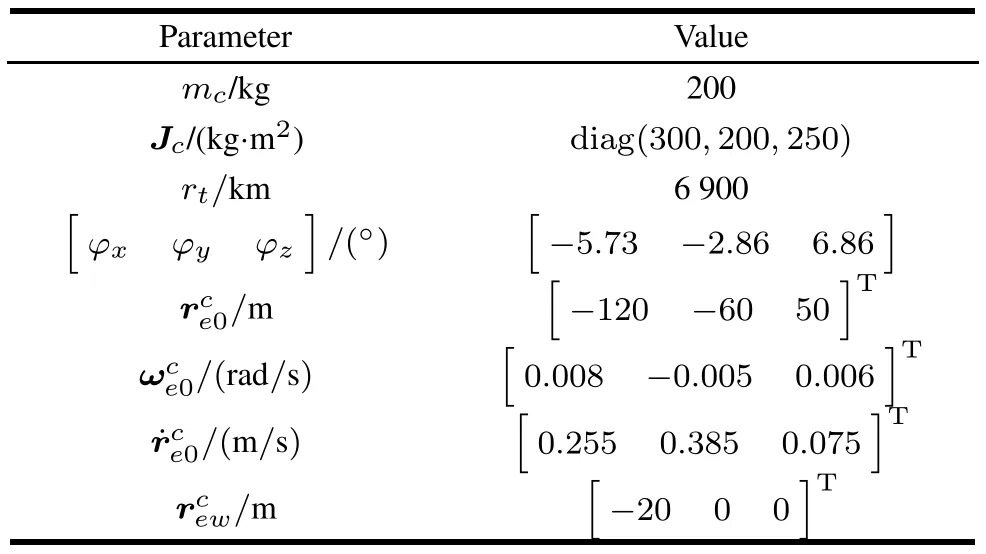
Table 2 Simulation parameters

Simulation results are shown in Fig.5–Fig.10.These quantities are all described in frameC.In Fig.5,ψx,ψy,ψzrepresent the angle attitude errors in three axes.In Fig.6,rex,rey,rezrepresent the relative positions in three axes.

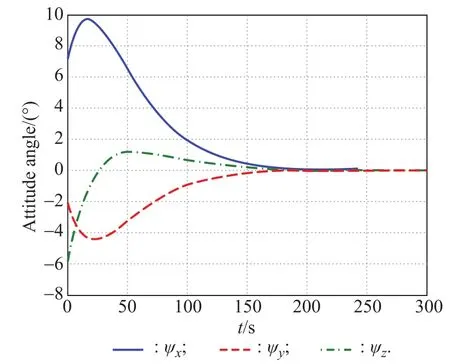
Fig.5 Attitude angle error curve

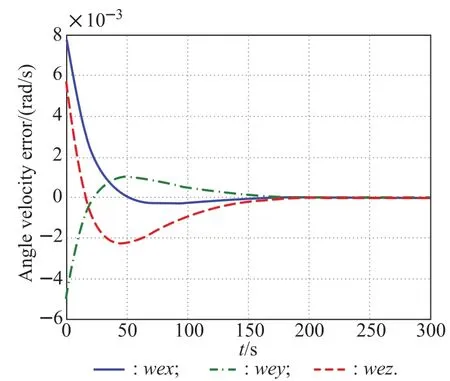
Fig.7 Angular velocity error curve

Fig.8 Velocity error curve

Fig.9 Control torque curve

Fig.10 Control force curve

In Fig.7,wex,wey,wezrepresent the angular velocity errors in three axes.In Fig.8,vex,vey,vezrepresent the velocity errors in three axes.In Fig.9,Tx,Ty,Tzrepresent the control torques in three axes.In Fig.10,Fx,Fy,Fxrepresent the control torques in three axes.

To show the control precision clearer, the orders of magnitude of different controlled variables are given in Table3.And we can see that the control accuracy at 300 s has already been very high.

Table 3 Control results at time of 300 s

6.Conclusions

To handle the coupling between position and attitude during the proximity relative motion of two spacecrafts,this paper uses dual quaternion to establish an integrated model of coupled relative posit on and attitude motion.As to the coupled relative motion,it has a unified description which is more compact,simpler and needs less target information than that using the traditional method.Firstly,introduce the foundation of dual quaternion systematically.Based on this,the detailed and clear modeling process are given,which provides an important reference for future researches.Then the 6D model is decomposed into two parts,which shows the couplings clearly and the decomposing form model can greatly facilitate the simulation model building in Matlab.Finally,a generalized PD control law is designed based on the integrated model established by dual quaternion.Simulation results show that the control law is effective and of high accuracy.

[1]SEGAL S,GURFIL P.Effect of kinematic rotation-translation coupling on relative spacecraft translational dynamics.Journal of Guidance Control&Dynamics,2012,32(3):1045–1050.

[2]XIN M,PAN H.Nonlinear optimal control of spacecraft approaching a tumbling target.Aerospace Science and Technology,2011,15(2):79–89.

[3]LU W,GENG Y H.Coupled control of relative position and attitude for on-orbit servicing spacecraft with respect to target.Acta Aeronautica et Astronautica Sinica,2011,32(5):857–865.(in Chinese)

[4]ZHANG Q Z,JIN Y Q,KANG Z Y,et al.Coupled control of relative position and attitude for servicing spacecraft approaching the target in close proximity.Systems Engineering and Electronics,2015,37(1):141–147.(in Chinese)

[5]SUN S H,JIA Y M.Attitude and orbit control of spacecrafts for motion reconstruction of flying around and approaching the tumbling target.CAAI Transaction on Intelligent Systems,2016,11(6):818–826.

[6]STANSBERY D T,CLOUTIER J R.Position and attitudecontrol of a spacecraft using the state-dependent Riccati equation technique.Proc.of the American Control Conference,2000:1867–1871.

[7]XING Y,CAO X,ZHANG S,et al.Relative position and attitude estimation for satellite formation with coupled translational and rotational dynamics.Acta Astronautica,2010,67(3):455–467.

[8]YANS U,KANGLI.Coupled relative attitude-orbit dynamics and control of anear satellites.Aerospace Control&Application,2014,40(4):20–25.(in Chinese)

[9]CHEN W,JING W,XIA X.Autonomous robust orbital and attitude coupling control of final proximity in rendezvous.Proc.of the IEEE International Symposium on Systems and Control in Aerospace and Astronautics,2009:1–6.

[10]ZHENG Z,ZHOU H,CHEN B,et al.Sliding mode control for satellite proximity operations with coupled attitude and orbit dynamics.Proc.of the IEEE International Conference on Intelligent Control and Information Processing,2011:824–829.

[11]SELIG J M.Geometric fundamentals of robotics.New York:Springer,2005.

[12]FISCHER I.Dual-number methods in kinematics,statics and dynamics.Boca Raton,USA:CRC Press,1998.

[13]FIGUEREDO L F C,ADORNO B V,ISHIHARA J Y,et al.Robust kinematic control of manipulator robots using dual quaternion representation.Proc.of the IEEE International Conference on Robotics and Automation,2013:1949–1955.

[14]GAO Y,LIU X P.Robot base frame calibration method based on dual quaternion.Journal of Mechanical&Electrical Engineering,2017,34(3):310–314.

[15]GAN D,LIAO Q,WEI S,et al.Dual quaternion based inverse kinematics of the general spatial 7R mechanism.Journal of Mechanical Engineering Science,2008,222:1593–1598.(in Chinese)

[16]NI Z S,LIAO Q Z,WU X X.General 6R robot inverse solution algorithm based on a quaternion matrix and a Groebner base.Journal of Tsinghua University(Science and Technology),2013,53(5):683–687.

[17]BRANETS V N,SHMYGLEVSKY I P.Introduction to strapdown inertial navigation systems.Moscow:Nanka,1992.

[18]ZHAO Y L,QIAO B,JIN Y Q,et al.An integrated relative navigation algorithm for spacecraft based on binocular vision and inertial measurement.Aerospace Control,2016,34(4):47–52.(in Chinese)

[19]FILIPE N,TSIOTRAS P.Adaptive position and attitudetracking controller for satellite proximity operations using dual quaternions.Journal of Guidance Control&Dynamics,2014,38(4):566–577.

[20]ZHU Z X,MA J J,FAN R S.Synchronization control of relative motion for spacecraft with screw theory based description.Acta Aeronautica et Astronautica Sinica,2016,37(9):2788–2798.

[21]WANG J Y,LIANG H Z,SUN Z W,et al.Relative motion coupled control based on dual quaternion.Aerospace Science&Technology,2013,25(1):102–113.

[22]WANG Q B,TANG S,MA K,et al.Relative position and attitude estimation of spacecrafts based on dual quaternion for rendezvous and docking.Acta Astronautica,2013,91(10):237–244.

[23]YANG Y D,JING W X,ZHANG Z.A new method for orbit and attitude coupling control problem of flexible spacecraft based on dual quaternions.Journal of Astronautics,2016,37(8):946–956.(in Chinese)

[24]GUI H,VUKOVICH G.Dual-quaternion based adaptive motion tracking of spacecraft with reduced control effort.Nonlinear Dynamics,2015,83(1/2):1–18.

[25]WANG X,YU C,LIN Z.A dual quaternion solution to attitude and position control for rigid-body coordination.Proc.of the IEEE International Conference on Bioinformatics and Biomedicine,2013:38–42.

[26]CHEN B L,GENG Y H.Relative motion coupled dynamic modeling between two docking ports.Systems Engineering and Electronics,2014,36(4):714–720.(in Chinese)