基于代理模型的喷水推进泵水力特性分析及优化

陈 杰，张孟杰，刘涛涛，*，吴 钦，叶哲豪

（1.北京理工大学 机械与车辆学院，北京 100081；2.中国北方车辆研究所，北京 100072）

0 引言

喷水推进作为一种特殊的推进方式[1]，相比于传统的螺旋桨推进，喷水推进泵具有结构紧凑、效率高及附体阻力小等优点，逐渐成为两栖车及船舶的主要推进方式[2-3]。

然而，两栖车及船舶在启航、加速以及转弯等状态时，喷水推进泵很容易进入空化工作区，空化的发生将直接导致喷水推进泵性能下降[4-5]。针对喷水推进泵的空化问题主要通过结构优化设计进行解决[6-8]，主要集中在试验优化设计[9]、速度系数法优化设计[10]、损失极值法优化设计[11]、计算流体力学（CFD）优化设计[12]以及多工况优化设计[13]等方面。但喷水推进泵结构往往较为复杂，工作环境恶劣，传统的优化方法都具有一定的局限性，或需要大量准确的公式推导，或有赖于设计者的经验和试验结果借助仿真软件进行多次重复建模才能得到设计目标的变化趋势。

近年来由Shyy等[14]提出的代理模型优化设计方法有效避免了传统优化方法的不足，可有效过滤数值仿真或者实验结果中的噪声，最大程度上保证设计结果的准确性，同时还可得到多目标的优化结果。Goel等[15]采用代理模型的方法对泵的叶片几何形状进行了优化，取得了理想的结果。赵宇等[16]以泵首、次级叶轮的叶片安放角以及相位角作为优化设计参数，以效率和压力系数为优化目标，采用代理模型的方法对某一串列泵进行优化设计，使得泵效率和空化性能均有所提升。吴钦等[17]利用代理模型分析方法对考虑了模型参数和物质属性的 Merkle空化模型在低温介质空化流动计算中的应用进行了评价和优化，提高了模型的预测能力。熊英华等[18]以诱导轮出口安放角和泵叶轮进口安放角为优化参数，泵扬程系数和空化余量为优化目标，采用代理模型的方法对某航空燃油泵进行优化设计，结果显示，优化后的燃油泵空化性能提高了18%。谷海涛等[19]以某种水下滑翔机为研究对象，构建机翼的代理模型优化设计方法，优化结果显示，滑翔机的运动性能提高，升阻比较之前提高了6.76%。Fan等[20]采用移动最小二乘法建立代理模型，对射流泵为研究对象进行全局优化，在泵输入功率减小20%的同时，效率提高4%。

本文采用代理模型优化方法对设计工况下的喷水推进泵结构参数进行优化分析，基于全局敏感度分析方法评价了叶轮叶片进出口安放角对喷水推进泵水力特性的影响，同时采用数值计算方法对优化后的喷水推进泵性能进行了分析。

1 数值计算方法

1.1 基本控制方程

研究采用均质平衡流模型，假设汽液两相为均相流动，相间无相对速度，考虑汽液两相间的传输速率，则基于Favre平均的Navier-Stokes方程为

1.2 基于标准SST k-ω模型的旋转修正湍流模型

由Menter提出的SST k-ω湍流模型[21]如下：

湍流粘性系数由下式确定：

式中：Pk为湍流生成项；Dk、Dω为湍流耗散项；F1、F2为混合函数；S为剪应力张量的常数项。

由于叶轮的高速旋转，推进泵内部流场具有强烈的旋转曲率效应，标准的SST k-ω涡粘模型难以捕捉强旋转和大曲率流动。为了解决这一问题，本文研究中基于局部涡旋运动效应对标准SST k-ω湍流模型k方程和ω方程中的Pk进行修正，旋转修正函数为

式中：r*和分别为当地涡旋运动引起的流线曲率和流场旋转效应；经验常数 Cr1=1.0，Cr2=2.0，Cr3=1.0。

考虑到数值计算稳定性的要求，计算中对旋转函数做如下限定：

则修正系数fr为

式中，Cscale为比例系数，默认值为1。

1.3 空化模型

计算采用基于 Rayleigh-Plesset空泡生长方程得到的Zwart空化模型[22]，则蒸发和凝结项为

式中：αnuc=5×10-4为空化核子体积分数；RB=1×10-6m为空泡半径；p和pv分别为当地压力和汽化压强；Cprod=0.01和Cdest=50分别为凝结和蒸发系数。

1.4 网格划分与边界条件设置

数值计算采用的轴流式喷水推进泵水力模型如图1所示，其主要的几何尺寸如表1所示，叶轮直径D=300 mm，设计转速 n=2 000 r/min，设计流量Qd*=0.802 m3/s，本文计算中流量范围为设定为0.85～1.1 Qd*。

表1 轴流式喷水推进泵主要参数Table 1 Main parameters of axial flow water-jet propulsion pump

图1 轴流式喷水推进泵水力模型及流道结构Fig.1 Hydraulic model and channel structure of axial flow water-jet propulsion pump

喷水推进泵采用六面体全结构化网格，其中进口段与出口段在ANSYS-ICEM中进行划分，叶轮和导叶区域在 ANSYS-TurboGrid中进行划分，近壁面区域采用分层网格局部加密处理，网格质量均在0.7以上，如图2所示。计算采用总压入口、质量流量出口边界，叶片及轮缘轮毂均采用无滑移壁面边界，壁面函数为标准壁面函数，动、静交接面采用Frozen Rotor类型，以单相计算结果作为初值，进行迭代计算空化流动。

图2 局部网格划分示意图Fig.2 Schematic diagram of local grid division

1.5 网格无关性及数值计算方法验证

为了对网格无关性进行验证，在相同计算条件下分别取网格数为320 W、360 W、400 W、440 W的网格进行计算。由于进、出口网格对整体性能影响较小，且在壁面处已进行加密处理，网格质量较高，计算中保持进、出口网格数量不变，只考虑叶轮和导叶的网格数量对外特性计算结果的影响，各流域的网格划分如表2所示。图3给出了在设计工况下（n=2 000 r/min，Qd*=0.802 m3/s）喷水推进泵外特性参数与网格数之间的关系，可以看出：随网格数的增加，推进泵效率变化范围较小；扬程系数和轴功率系数在网格数为400 W后基本保持不变。综合考虑网格质量对计算结果的影响以及计算的经济性，最终选择轴流式喷水推进模型泵的计算网格数为400 W。

表2 轴流式喷水推进泵各流域网格划分Table 2 Grid division of each basin of axial flow water-jet propulsion pump

图3 网格无关性验证Fig.3 Grid independence verification

为了进一步对数值计算方法的准确性进行验证，图4和图5分别给出了轴流式喷水推进泵在设计转速（n=2 000 r/min）、不同流量范围0.85～1.1 Qd*时实验和数值计算得到的外特性曲线和设计流量下的空化特性曲线。通过对比可以看出，数值计算得到的外特性与实验结果一致性较好，扬程、轴功率和效率误差均在 5%以内。二者间存在误差的主要原因是：实验中存在弯管损失、实验台存在测量误差以及实际加工精度存在误差等。从空化特性曲线可以看出，随着NPSH的降低，模型泵扬程起初并未发生明显波动，当NPSH下降到11.91 m时，扬程急剧下降，数值预测的扬程随NPSH的变化趋势与试验结果基本一致。试验中模型泵临界空化余量为11.91 m，略高于数值计算结果，这可能是由于水中可能含有少量空气或者杂质颗粒使管路系统中发生空化。由此说明，本文所采用的数值计算方法可以较准确地对泵的性能进行预测。

图4 喷水推进泵外特性曲线Fig.4 External characteristic curve of water-jet propulsion pump

图5 喷水推进泵空化特性曲线Fig.5 Cavitation characteristic curve of water-jet propulsion pump

2 结果与分析

2.1 喷水推进泵水力特性分析

图6给出了设计工况下模型泵的空化特性曲线，可以看出随着NPSH的降低，喷水推进泵的空化特性曲线可分为空化初生、空化发展以及空化充分发展 3个阶段，如图6中（Ⅰ）、（Ⅱ）、（Ⅲ）所示。在空化初生阶段（12.73 m＜NPSH＜24.79 m），扬程系数基本保持不变；在空化发展阶段（11.8 m＜NPSH＜12.73 m），扬程系数先在小范围内波动，后急剧下降，在 NPSH=11.8 m时，下降幅度超过 5%，出现扬程断裂现象；在空化充分发展阶段（NPSH＜11.8 m），扬程系数进一步下降，泵无法正常工作。效率和轴功率变化趋势与扬程变化趋势类似。

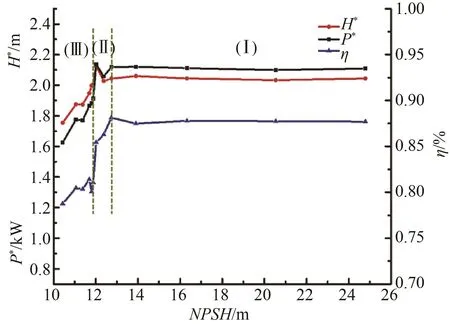
图6 轴流式喷水推进泵空化特性Fig.6 Cavitation characteristics of axial flow water-jet propulsion pump

为进一步分析喷水推进泵的空化特性，图7给出了不同NPSH条件下数值预测的叶轮叶片表面空穴形态与试验的对比。从图中可以看出，当NPSH=24.79 m时，叶轮表面未发生空化。随着NPSH的逐渐降低，进口区域靠近轮缘处及出口区域的叶顶间隙处首先出现空化现象，并逐渐向叶片中部延伸。当NPSH进一步降低，叶顶间隙处开始发生空化，并向流道内扩张，导致间隙处局部流速升高，压力降低，叶片工作面和背面的压差增大，即叶片做功能力增加，扬程和轴功率升高；同时，由于叶轮旋转与轮缘产生相对运动，导致叶顶空化形状近似三角形，且空化区域由轮缘向轮毂延伸，当 NPSH降低至 11.8 m时，空化区域覆盖整个叶片表面，结合图6可以看出，此时空化特性曲线陡降，泵开始失效。

图7 叶轮叶片表面空穴分布对比（σv=0.1）Fig.7 Comparison of cavitation distribution on impeller blade surface（σv=0.1）

图8给出了叶轮叶片进、出口安放角等不同设计参数在设计工况下的效率曲线，其中C1和C2分别表示叶轮的进口安放角和出口安放角。从图中可以看出，设计参数叶轮叶片进口安放角β1和出口安放角β2对推进泵的效率具有明显影响。当 C1＞0°、C2＞0°时，推进泵的效率随着流量的增大先增大后趋于不变；当C1＜0°、C2＜0°时，推进泵的效率随着流量的增大呈下降趋势，尤其是叶轮叶片进、出口安放角分别为C1=-5°和 C2=-2°时，其效率下降速率明显增大，在Q*/Qd*=1.1时，效率已经下降至η=0.48。

图8 不同叶轮叶片进、出口安放角下喷水推进泵的效率曲线Fig.8 Efficiency curve of water-jet propulsion pump with different impeller blade angles at inlet and outlet

2.2 基于代理模型的结构参数优化设计

轴流式喷水推进泵的叶片安放角对其性能具有重要的影响，通过数值计算的方法寻求最优的结构参数，计算量大且计算周期较长，因此采用合理、高效的数值优化方法获取空化性能和外特性最优时推进泵的结构参数至关重要。

2.2.1 代理模型及优化分析

轴流式喷水推进泵的叶片安放角对其性能具有重要的影响，通过数值计算的方法寻求最优的结构参数，计算量大且计算周期较长，因此采用合理、高效的数值优化方法获取空化性能和外特性最优时推进泵的结构参数至关重要。基于代理模型的优化设计方法是一种计算量小、精度高的分析方法，其实质是通过离散的数据点，建立精度较高的数学模型，拟合出反映目标变量和自变量之间关系的函数，分析目标变量和自变量的敏感性以及对自变量取值进行寻优。基于上述的分析，本文选取叶轮进口安放角 C1和出口安放角 C2作为代理模型的自变量，选取效率和轴功率作为目标变量，具体的优化流程如图9所示。

图9 轴流式喷水推进泵优化设计流程图Fig.9 Flow chart of optimization design for axial flow water-jet propulsion pump

选取叶片安放角为 0°时的喷水推进泵作为基础模型，以叶轮进、出口安放角作为自变量，样本空间取值范围如表3。结合拉丁超立方法和中心复合法生成30组样本点，每组样本点包含C1、C22个参数，将样本空间归一化，如图10所示，其中安放角增加-4°时为0，增加4°时为1。根据样本点信息绘制30组喷水推进泵模型，采用CFX针对喷水推进泵进行数值计算后获得30组目标变量值。

表3 样本空间Table 3 Sample space

图10 样本点归一化分布Fig.10 Normalized distribution of sample points

根据30组数值计算的结果分别选取Kriging模型（KRG）、项式响应面近似模型（PRS）、辐射神经元网络近似模型（RBNN）及加权平均值近似响应模型（WAS）等4种代理模型近似方法对数值计算结果进行数据拟合，并采取均方根误差（Root Mean Square Error，RMSE）方法针对代理模型的拟合精度进行评价，其表达式为

式中：n为测试点数目；xi为第i个测试样本点；y(xi)为测试点的实际响应值；ˆy(xi)为预测响应值。

表4给出了各代理模型对目标变量的拟合误差，可以看出不同代理模型对样本数据的拟合精度存在较大差异。其中KRG模型对轴功率和效率的拟合精度最差；PRS和 RBNN模型的拟合精度较好，但仍然存在提升空间；WAS模型的拟合精度最高。由于WAS模型基于上述3种代理模型的误差进行了权重分配，故其对目标变量的拟合精度最高。因此，本文的后续研究将采用WAS模型作为最优的代理模型。

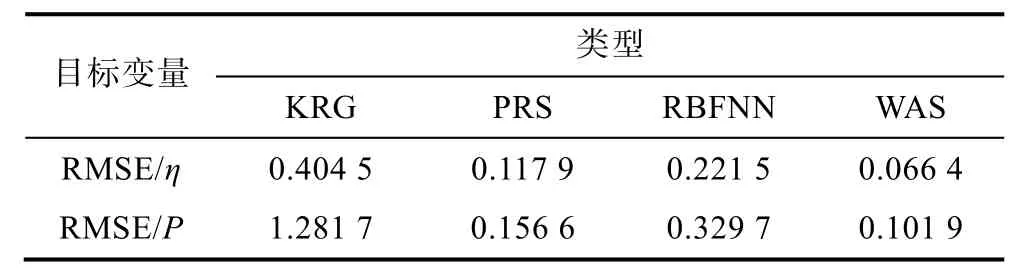
表4 代理模型误差评价Table 4 Error evaluation of surrogate model

2.2.2 敏感度分析及结构参数优化

为了对喷水推进泵的结构参数进行优化，首先需要对涉及到的结构参数进行敏感度分析。敏感度分析是指利用代理模型对喷水推进泵在设计工况下的数值计算结果进行拟合，比较自变量的偏方差和总方差以获得自变量β1和β2对目标变量效率η和轴功率P的重要程度分析。图11给出了采用Sobol方法对WAS代理模型的10 000组拟合数据进行全局敏感度分析的结果，其中C1为叶轮进口安放角，C2为叶轮出口安放角。从图中可以看出，叶轮叶片进口安放角C1在目标变量轴功率P的全局敏感度分析中所占比重为 68%，出口安放角C2所占比重为32%，说明目标变量轴功率P受叶轮出口安放角C2影响较大；而在对目标变量效率 η的敏感度分析中，各自变量所占比重差异较大，C1所占比重高达95%，而C2的比重仅为5%，说明目标变量效率η主要受叶轮出口安放角C2的影响。

图11 WAS代理模型自变量对目标变量的全局敏感度分析Fig.11 Global sensitivity analysis of independent variables to target variables in WAS proxy model

图12给出了WAS代理模型拟合结果在目标变量空间中的分布情况，其中x轴为轴功率、y轴为效率，绿色圆点为10 000个样本点。由图可知，喷水推进泵结构参数多目标优化问题不存在最优解，所有可能的解都只满足一个目标变量的最佳取值，并构成Pareto最优解集（红色点集），其最优解集分布在样本空间右上方。

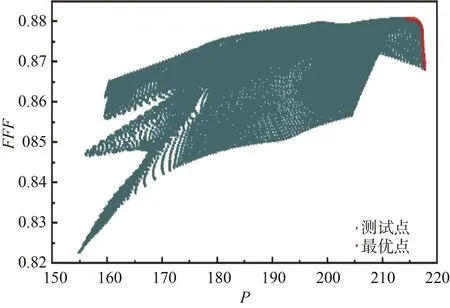
图12 目标变量空间分布Fig.12 Spatial distribution of target variables

图13给出了Pareto最优解集在其自变量空间的分布情况，可以看出，最优解在自变量空间内主要集中在3个区域。考虑到本次优化的最终目标是在具有较高效率的同时保证尽可能高的轴功率，为此在这3个区域分别选取一个最优的样本点进行二次数值计算，表5为所选取的样本点的相关参数及代理模型预测结果。

图13 最优解集在自变量空间的分布Fig.13 Distribution of optimal solution set in independent variable space

表5 3组样本点参数及代理模型优化结果Table 5 Optimization results of parameters and surrogate model of three groups of sample points

针对上述优化点分别建立喷水推进泵模型，并采用CFX方法对设计工况下推进泵性能进行数值计算，其结果如表6所示。由表可知：设计工况下样本点2的效率最高，样本点3的轴功率最高。综合上述分析，为满足效率较高的同时轴功率尽可能高的要求，选择样本点2为最终优化结果，此时喷水推进泵叶轮叶片的进口安放角C1=0.69°，出口安放角C2=3.92°。

表6 设计工况下3组样本点的数值计算结果Table 6 Numerical calculation results of three groups of sample points under design conditions

2.2.3 优化后喷水推进泵性能分析

图14给出了优化前后喷水推进泵的外特性曲线，从图中可以看出，优化前后的喷水推进泵外特性曲线变化趋势基本相同，即随流量的增加，扬程逐渐下降，轴功率逐渐上升，效率先上升后下降。优化后的扬程和轴功率在不同流量工况下较优化前均有所提升，效率的提升主要体现在在设计工况和大流量工况，其最大效率点出现在Q*/Qd*=1.0处。总体而言：优化后喷水推进泵外特性较优化前有所提升，效率最高为88.54%，较优化前提高了约1.7%；此时功率密度约为2.91 MW/m2，较优化前提高了约6%。

图14 优化前后喷水推进泵外特性对比Fig.14 Comparison of external characteristics of water-jet propulsion pump before and after optimization

图15对比了设计工况下优化前后喷水推进泵在10%、50%和90%叶高处叶轮叶片吸力面和压力面压力沿流向的分布，由图可以看出，优化前后叶轮叶片表面的压力沿流向分布规律类似，即叶轮进口及出口处压力变化较为剧烈，叶轮中部压力变化相对均匀。同时，优化后的叶片在10%、50%叶高处的吸力面和压力面的压差较优化前增大，说明喷水推进泵的做功能力增加，性能得到提升。优化后的叶片在90%叶高处的压力分布较优化前更为均匀，说明叶轮出口处的流动脱落现象得以改善。

图15 优化前后叶轮叶片表面压力沿流向分布Fig.15 Distribution of surface pressure of impeller blade along flow direction before and after optimization

为进一步评价优化后的喷水推进泵性能，图16给出了优化前后推进泵在不同空化阶段的空穴形态对比。从图中可以看出，随着NPSH的下降，叶轮叶片吸力面前缘开始产生空泡，并逐渐向后发展直至覆盖整个叶片；在相同进口条件下（即 NPSH相同），优化后的推进泵吸力面空穴面积较优化前均有所减小，说明优化后的喷水推进泵空化性能也得到了一定的提高。

图16 优化前后叶轮叶片表面空穴形态对比（σv=0.1）Fig.16 Comparison of cavitation morphology on impeller blade surface before and after optimization（σv=0.1）

3 结束语

本文基于旋转修正的SST k-ω湍流模型和Zwart空化模型对轴流式喷水推进泵的水力特性进行了数值计算研究，基于数值计算结果，采用代理模型优化方法，对喷水推进泵的叶轮进出口安放角等结构参数进行了优化设计，得到以下结论：

1）采用的数值计算方法能够准确地预测喷水推进泵的外特性和空化特性，并基于数值计算结果发现叶轮的进口安放角和出口安放角对喷水推进泵的水力特性影响较大。

2）通过代理模型优化分析，喷水推进泵叶轮出口安放角对其效率和轴功率影响占比分别约为 95%和68%，进口安放角对其效率和轴功率影响占比分别约为5%和32%，说明喷水推进泵效率和轴功率主要受叶轮出口安放角的影响。

3) 当叶轮进口安放角和出口安放角分别为0.69°和3.92°时，满足Pareto最优解，此时喷水推进泵效率较优化前提高了约 1.7%，功率密度较优化前提高了约6%，模型泵的整体优化效果明显。