基于小波分析的侧扫声呐信号非线性增强算法
王 磊,金绍华,崔 杨,边 刚,魏 源,3
(1.海军大连舰艇学院 军事海洋与测绘系,辽宁 大连 116018;2.中国人民解放军92763部队,辽宁 大连 116041;3.中国人民解放军 91937部队,浙江 舟山 316002)
0 引言
侧扫声呐探测技术是水下目标或海底探测的重要手段之一。由于其独特的成像机制限制和海洋中大量噪声的影响,导致形成图像的质量相对较差,特别是在图像细节方面,对比度低、边缘模糊,这对水下目标识别、分类等影响很大。为此,往往在侧扫声呐图像降噪的同时需要对图像进行增强处理,以突出感兴趣部分信息,获取更好的视觉效果。
图像增强是指有目的地强调图像的整体或局部特征,突出感兴趣的特征,以满足某些特殊分析的需要[1]。传统的图像增强方法主要有空间域增强和频率域增强。空间域增强主要是对图像像素灰度值进行处理,如直方图均衡化[2]、反锐化掩膜[3]等,但利用空间域增强的同时往往也增强了噪声信号,导致图像后期处理困难。频率域增强主要是将图像由时域转换到频域,对频域内系数进行相应处理,达到增强图像目的,如基于傅立叶变换算法、频域同态滤波[4]等,但以上频率域处理方法会造成部分细节丢失。
通过小波变换对小波系数进行处理,在增强图像细节特征的同时抑制噪声是图像增强的有效方法之一,并在红外图像、超声图像处理中得到了广泛应用[5-6],但在侧扫声呐图像的增强处理中应用的还不多。由于小波变换仅对一维信号中的点奇异特征敏感,只能表达水平、竖直和对角方向上的信息,不能较好表示多维信号中的方向信息,会造成细节部分表现不充分,因此小波变换在多维信号处理当中存在不足。侧扫声呐的降噪处理可分为ping[7](呯,声呐脉冲,侧扫声呐发射阵元每隔一段时间发射一个短脉冲,经反向散射接收到的回波序列称为一个 ping)数据处理和声呐图像数据处理[8],目前大多数侧扫声呐图像处理均基于声呐图像数据[9-11],基于ping数据进行处理的很少。本文选取了侧扫声呐 ping信号数据进行一维小波变换,利用非线性函数处理高频信息和低频信息,再经过反变换重构信号。实测数据实验表明:该方法较好地发挥了小波变换处理一维信号的优势,可以同时实现侧扫声呐图像的增强和噪声的抑制,获取良好的视觉效果。
1 基于小波变换的非线性增强
利用小波变换对 ping信号进行非线性增强的核心是对小波分解后的小波系数进行非线性增强处理,该算法包含2部分:小波阈值降噪和小波系数的非线性增强。
1.1 小波阈值降噪
分解后的小波系数中,包含了信号的信息部分和噪声部分。其中幅值较大、数目较少的为信息部分,多分布于低频;而幅值较小、个数较多的为噪声部分,多分布于高频。基于这一特征,把绝对值较小的系数置为0,保留或伸缩绝对值较大的系数,再利用变换后的小波系数进行信号重构,即可达到降噪的目的。该过程主要涉及小波基的选择、分解层数的选择以及阈值的选择,其中最关键的是阈值选择。通常侧扫声呐ping信号波动较大,是一种非稳态信号,此类信号分解更适用 db小波基[12];分解层数选择上,层数越大,越利于信号与噪声分离,但同时失真也越大,侧扫声呐ping信号噪声水平较高,导致信噪比降低,在分解层数较大时才能更好地进行噪声抑制;阈值选择通常采用以下几种。
1)Visushrink阈值。
即通用阈值,其计算方法为

式中:σ为噪声标准差;N为信号长度。该方法认为与噪声相关的小波系数大于该阈值的概率趋于0,但该方法中阈值大小与信号长度相关,信号长度越大,阈值越大,可能估计阈值远大于实际,造成过多的消除有用信息。
2)K-Sigma阈值。


式中:σ为噪声标准差,实际中k取3~4之间。该方法认为当噪声为正态高斯分布时,与噪声相关的小波系数大于3σ的概率趋于0。尽管该方法下阈值大小与信号长度无关,但未考虑小波分解各尺度下噪声影响的不同,采用同一k值无法有效去除不同尺度下的噪声。
3)Sureshrink阈值。
即Stein无偏风险阈值,是一种基于Stein的无偏似然估计自适应阈值。其阈值风险函数为

式中:wi为某一尺度小波系数;N为该尺度系数个数。以风险函数中的最小值rmin为风险值所得到对应的小波系数wmin,求取SureShrink阈值:

式中,σ为噪声标准差。该阈值应用较多,但运算较为复杂。
4)BayesShrink阈值。
该阈值为大量实验得出的最佳阈值,是对各尺度小波系数进行Bayes最小风险估计得到的:

σk为第k尺度下小波系数标准差:

式中:N为该尺度小波系数个数;wi为某一尺度小波系数;σ为噪声标准差。BayesShrink阈值理论的提出与应用是建立在以经验观察为背景的基础上,计算较SureShrink阈值更为简单,因此被广泛应用在图像处理领域中[13]。
随着小波分解尺度的不断增加,噪声集中的能量分布逐渐减小,此时采用同一阈值易去除不同尺度下高频分量中的有用信息。本文采用了一种改进的 BayesShrink阈值选择方法[14],将其应用到侧扫声呐 ping信号处理中,并根据 ping信号特征加以修正。

由上式可见,尺度越大,阈值越小,符合小波变换后噪声分布的特性。该方法考虑了小波分解尺度影响和各尺度下噪声特性,可以克服统一阈值的不足,增强算法的自适应性。
在真实 ping信号处理中,由于无法事前获取真正的噪声强度,因此需要对噪声标准差进行估计。利用经典中值估计公式进行噪声标准差估计是常用的方法之一:

式中:Median为取中值;wi为某一尺度下高频小波系数;0.647 5为经验常数。
1.2 非线性增强
基于小波分析的非线性增强的实质是利用非线性增强函数来映射各级小波系数[15]。对侧扫声呐ping信号进行增强就是在抑制噪声的同时对高、低频小波系数进行不同类型的伸缩变换,达到增强目的。侧扫声呐信号概貌信息和缓慢变化部分通常表现为低频分量,噪声和目标细节部分通常表现为高频分量。以某侧扫声呐ping信号为例,进行3层db5小波分解结果如图1所示。

图1 ping信号及小波分解图Fig.1 Diagram of ping signal and wavelet decomposition
由图1和以上分析可知,侧扫声呐ping信号低频小波系数模值相差小,曲线变化平缓,而在高频中边缘细节的小波系数相对较大,曲线变化剧烈。一般可将增强函数仅作用于高频分量,而低频分量不变。但侧扫声呐信号形成图像整体对比度低,细节不明显,所以可以选择对低频和高频分量小波系数分别进行非线性函数处理,以提高图像的整体质量。
1.2.1 高频系数的非线性增强
选取合适的非线性函数对高频小波系数进行增强,需要满足以下几点要求。
1)保持信息部分中较小的系数增强较小,较大的系数增强较大,同时避免噪声的小波系数被增强。
2)保持小波系数的原有特征,保证非线性增强函数的单调性,避免出现新的极值点。
3)保持小波系数的相位极性,保证非线性增强函数的反对称,避免出现“振铃”现象。
本文选取增益函数[16]


图2 高频非线性增益函数曲线Fig.2 Curve of high-frequency nonlinear enhancement function
根据式(7)-(8)对高频小波系数进行阈值化处理,可得

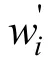
1.2.2 低频系数的非线性增强
侧扫声呐信号低频分量反映概略信息,一般含噪声较少,由于其系数值相对较小,需通过拉伸得到更好的增强效果。选取合适的非线性函数对低频小波系数进行增强,需要满足以下几点要求。
1)非线性函数为单调函数,初始段缓慢增长,中间段快速增长,结尾段缓慢增长,即呈现s型。
2)非线性函数参数易控制,可以方便控制拐点位置和快速增长段斜率。
本文选取增益函数[17]

进行低频系数非线性增强,其中e决定增长区位置,d决定快速增长区斜率。图3为该增益函数曲线,其中d=10,e=4。

图3 低频非线性增益函数曲线Fig.3 Curve of low-frequency nonlinear enhancement function
将该增益函数用于低频小波系数,可得

式中:C、C′分别为增强前后的低频小波系数;Cmax为低频小波系数的最大值;k′为常数,通常大于1。
2 实验结果及分析


式中,S、P分别为改正前后的声幅值。
图4中原始图像偏暗,整体不清晰,噪声水平较高。以图中红色标记区域为例,经直方图均衡化处理后,部分区域明显亮度过高,同时噪声被放大,噪点明显较多,细节和边缘未得到有效的增强;经同态滤波增强处理后,图像细节和边缘得到改善,但噪点仍比较明显;经二维小波增强处理后,细节轮廓和整体噪声水平得到较大改善,但图像仍稍显模糊;经本文方法处理后,图像整体对比度提高,抑制噪声效果较明显,且边缘和细节得到较好的保留,图像视觉效果较好。
图5为失事飞机区域放大图。以图中红色标记区域为例,原始图像较暗,较难分辨轮廓和细节信息;直方图均衡化后,该区域噪点明显,呈现一片白色,掩盖了有效信息;同态滤波和二维小波增强后,轮廓较完整,但图像整体模糊;本文方法处理后轮廓和细节均较明显,且图像整体清晰度较高。为进一步验证本文方法的效果,本文采用信噪比进行量化评价,结果如表1所示。数据结果表明:本文方法量化结果好于其它几种方法,信噪比较其它方法平均提高了约16.3%,说明该方法较其它几种方法具有更好的噪声抑制能力。

表1 各增强方法评价指标对比表Table 1 Evaluation index contrast table of various enhancement methods

图5 侧扫声呐图像局部增强对比Fig.5 Contrast of side scan sonar image local enhancement
3 结束语
本文基于一维小波对侧扫声呐 ping声幅序列进行分解,采用不同的非线性函数对分解后的高、低频小波系数进行增强处理,再通过小波反变换重构 ping信号,获取处理后的侧扫声呐图像。实验结果表明:本文算法能够有效提升侧扫声呐图像整体对比度,利用该算法获取的视觉效果和定量指标均优于基于声呐图像数据进行处理的直方图均衡化、同态滤波增强和二维小波变换增强方法,在侧扫声呐图像增强处理上具有一定的应用价值。

