基于ALE方法的航行器跨介质冲击载荷研究
刘超维
(中国船舶重工集团公司第705研究所,陕西 西安 710077)
0 引言
航行器跨介质是非常复杂的流固耦合[1]问题,以跨水介质为例,其过程可分为撞水阶段、侵水阶段、带空泡航行阶段和全侵湿阶段。在跨介质初期的撞水阶段、侵水阶段航行器会承受极大的冲击载荷[2],对航行器壳体及其内部组件产生较大的危害。目前的航行器设计,只能依靠工程师经验以及简要仿真计算来得到其的跨介质条件,冲击载荷计算模型过于简化,计算结果误差较大,无法指导工程设计。对于某些垂直、高速情况下跨介质的航行器而言,其流固耦合作用变的更加复杂,极大增加了计算跨介质载荷的难度,因此,开展航行器跨介质冲击载荷研究意义重大。
关于跨介质弹道问题的研究,最早可以追溯至19世纪末20世纪初有关结构跨介质问题的研究。1929年,Von Karman[3]基于动量守恒定理和附加质量法解决了水上飞机在降落过程中的跨介质冲击载荷问题。Wagner[4]于1932年对Von Karman的方法进行修正,引入了水波影响因子,提出小斜升角模型的近似平板理论,使其结果更加符合实际,奠定了跨介质冲击研究的基础,此阶段国内关于航行器跨介质冲击载荷的计算分析研究较少。
随着数值技术和计算机科学的发展,数值方法处理跨介质砰击问题及弹道问题显示出了较大的优越性。L.Facci[5]等用CFD方法对多曲率结构的流固抨击进行了计算,并通过PIV试验证明了CFD方法在计算水中速度场、水动力载荷分布以及冲击过程中的能量传递方面的准确性。陈诚等[6]对超空泡航行器 20°角倾斜入水冲击载荷特性进行了试验研究。西北工业大学潘光[7]等对空投刚性体鱼雷垂直跨介质时流体动力进行了数值计算。张岳青等[8]进行了结构物入水冲击表面压力的模型研究及应用,分析了不同质量、不同结构物形状对入水冲击表面压力的影响。胡明勇[9]等人利用对低亚声速射弹跨介质时空泡、流场与弹道间的多介质耦合问题进行了数值计算,得到了不同跨介质条件下深度、速度变化曲线和空泡面闭合、空泡深闭合时间。
本文以航行器为研究对象,研究了不同跨介质速度及跨介质角度对冲击载荷的影响规律,为航行器跨介质弹道及外形结构设计提供一定参考。
1 流固耦合模型
1.1 ALE方法
ALE方法兼具欧拉(Euler)方法与拉格朗日(Lagrange)方法两者的特长,在建立几何模型和进行网格划分时,结构采用 Lagrange单元,而流体采用Euler单元,Lagrange结构与Euler流体的几何形状以及网格可以重合。在计算过程中,Euler流体流动时产生的压力载荷与 Lagrange结构网格相互作用。采用罚函数耦合方法对 Lagrange结构进行约束,将结构相关参数传递给流体单元。
罚函数耦合方法通过罚函数系数追踪Lagrange结构(从物质)和Euler流体(主物质)之间的相对位移d,检查每一个从节点对主物质表面的贯穿情况,如果不贯穿就不进行任何操作;如果出现贯穿,界面力F就会分布至Euler流体的节点上,界面力F的大小与贯穿的数量成正比:F=kid,式中ki为基于主从模型特性的刚度系数。
在每一个时间步积分上都要对界面力F进行计算,将它作为一个外部体积力,影响 Lagrange结构和Euler流体的加速度、速度、位移的变化。
ALE 方法下的控制方程包括质量、动量和能量守恒方程:
1)质量守恒方程:
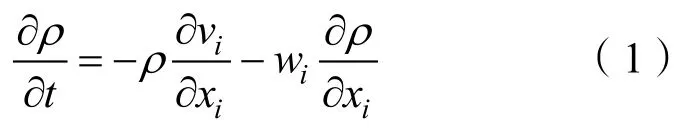
2)动量守恒方程:
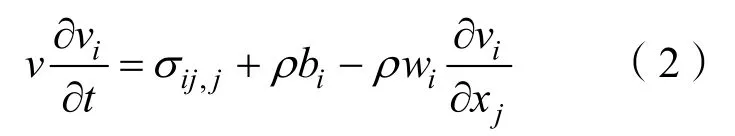
3)能量守恒方程:
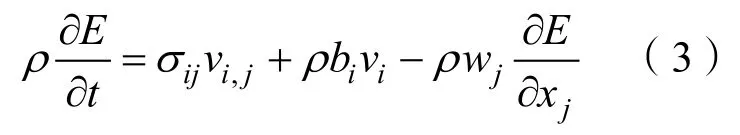
1.2 航行器的三维模型
利用三维建模软件 UG进行航行器的三维建模,航行器的具体尺寸参数如表1所示。

表1 航行器结构参数Table 1 Structural parameters of UUV
根据航行器的结构参数,在UG中进行航行器的三维建模,航行器的三维模型如图1所示。

图1 航行器的三维模型图Fig.1 Three-dimensional model diagram of UUV
1.3 有限元模型
在进行航行器跨介质冲击仿真计算时,ANSYS/LS-DYNA采用cm-g-μs单位制。
首先,选择网格划分需要的显式单元,本文中选择的单元类型是SOLID164单元。然后定义航行器、水、空气的材料模型,本文中航行器的材料为钢材,选择*MAT_PLASTIC_KINEMATIC材料模型作为航行器的材料模型,流体材料水和空气选择空材料模型*MAT_NULL来描述,水的状态方程采用Gruneisen状态方程来描述:
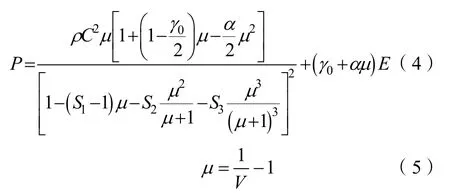
式中:P为压力;V为相对体积;E为单位体积内能;C、S1、S2、S3、0γ为水的材料常数。
空气材料状态方程采用 LINER-POLYNOMIAL线性状态方程来描述:

式中:P为压力;V为相对体积;E为单位体积内能;c0、c1、c2、c3、c4、c5、c6为空气的材料参数。
将航行器的三维模型导入到 ANSYS/LSDYNA中进行有限元的前处理,为了减少网格数量,节约计算时间,导入航行器的三维模型进行有限元建模时,取航行器的二分之一模型,将航行器的三维模型进行有限元网格划分,共有节点 4 768个,航行器有限元模型图如图2所示。

图2 航行器的有限元模型Fig.2 Finite element model of UUV
在 ANSYS/LS-DYNA中建立水域和空气域的三维模型,并进行网格划分。空气域的模型尺寸为3 000 mm×500 mm×1 500 mm,划分网格后共有18 000个节点;水域的模型尺寸为 3 000 mm×4 000 mm×1 500 mm;划分网格后共有144 000个节点。航行器的跨介质有限元模型如图3所示。
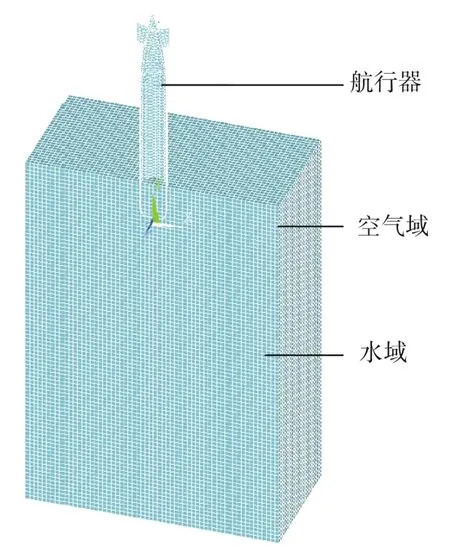
图3 航行器的跨介质有限元模型Fig.3 Cross-medium finite element model of UUV
2 航行器跨介质冲击流场
航行器在触水的瞬间,在触水点会产生压力冲击波,该冲击波会在水中迅速传播,在后续时刻,航行器会有更多的触水点,也会产生更多的冲击波。不同时刻压力冲击波变化如图4所示。
由图4可以看出,在航行器跨介质过程中,跨介质冲击压力有以下几点基本规律:1)航行器的跨介质冲击压力峰值发生在航行器跨介质的初期,即航行器刚触水时刻;2)航行器的跨介质压力冲击波从航行器与水域的接触点沿径向进行传播,并且距离流固耦合面越远,压力值越小;3)航行器的跨介质冲击压力波压力峰值,随着跨介质过程逐渐减小。

图4 航行器跨介质不同时刻压力云图Fig.4 Stress cloud diagram of UUV at different moments across medium
3 航行器跨介质冲击载荷
3.1 跨介质冲击载荷
在航行器跨介质瞬间(ms级),水介质会对航行器产生巨大的冲击力,后续时刻,航行器受到的跨介质冲击力迅速减小,并在一个较小范围内震荡。航行器垂直跨介质过程中受到的跨介质冲击轴向载荷与径向载荷变化过程分别如图5与图6所示。

图5 航行器跨介质冲击轴向载荷曲线图Fig.5 Cross-medium impact axial load curve diagram of UUV
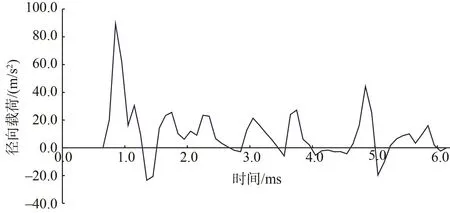
图6 航行器跨介质冲击径向载荷曲线图Fig.6 Cross-medium impact radial load curve diagram of UUV
航行器在跨介质过程中,由于受到跨介质冲击压力的作用,航行器的跨介质速度会随着跨介质深度的增加逐渐减小,航行器跨介质过程中跨介质速度随时间的变化如图7所示。

图7 航行器跨介质速度时间曲线图Fig.7 Cross-medium velocity-time curve diagram of UUV
由图4-7可以看出,在航行器跨介质过程中,跨介质冲击载荷和跨介质速度有以下几点规律:
1)航行器跨介质冲击载荷峰值发生在航行器跨介质冲击的初期,在航行器跨介质过程开始的1 ms内冲击载荷即达到峰值;
2)航行器的跨介质冲击载荷在达到峰值之后迅速减小,并一直保持在一个较小的范围内震荡;
3)航行器在垂直跨介质过程中,主要受到轴向冲击载荷作用,径向冲击载荷的大小明显小于轴向载荷;
4)由于受到航行器的跨介质冲击载荷作用,航行器的跨介质冲击速度随着跨介质过程的推进逐渐减小,并且在航行器的跨介质初期,由于受到较大的跨介质冲击载荷,速度减小较快,随后速度减小逐渐平缓。
3.2 跨介质速度的影响
航行器以不同的速度垂直跨介质时,跨介质冲击载荷峰值随速度的变化如图8所示。
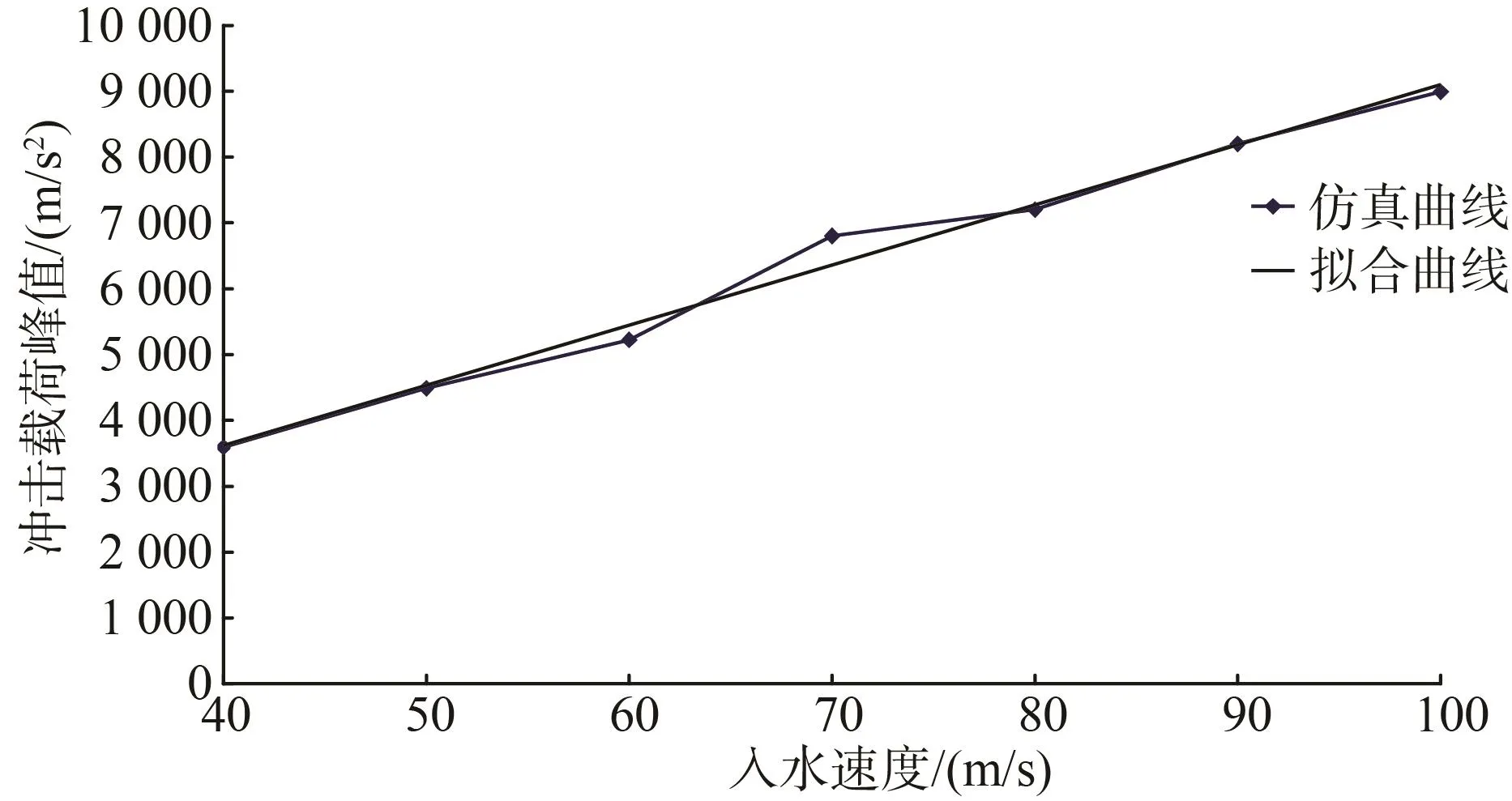
图8 航行器跨介质载荷峰值-跨介质速度曲线Fig.8 Cross-medium load peak-cross-medium velocity curve diagram of UUV
由图8看出,航行器垂直跨介质时,航行器的跨介质冲击载荷峰值随着航行器跨介质速度的增大而增大,对航行器的跨介质载荷峰值与跨介质速度进行曲线拟合,得到拟合曲线:

式中:y为航行器跨介质冲击载荷峰值;x为航行器的跨介质速度(40~100 m/s);2σ 为曲线的拟合方差。
由拟合曲线的方程以及拟合方差可以看出,航行器垂直跨介质的跨介质载荷峰值与速度基本成线性关系,在航行器垂直跨介质时,可根据方程估算航行器的跨介质载荷峰值,对仿真计算以及实验有一定的指导意义。
3.3 跨介质角度的影响
对航行器以 50 m/s的跨介质速度不同跨介质角度跨介质进行仿真,得到航行器不同跨介质角度跨介质时的跨介质冲击载荷峰值。航行器轴向载荷峰值、径向载荷峰值以及总的载荷峰值随航行器跨介质角度的变化如图9-11所示。

图9 航行器跨介质轴向载荷峰值-跨介质角度曲线Fig.9 Cross-medium axial load peak-cross-medium angle curve diagram of UUV
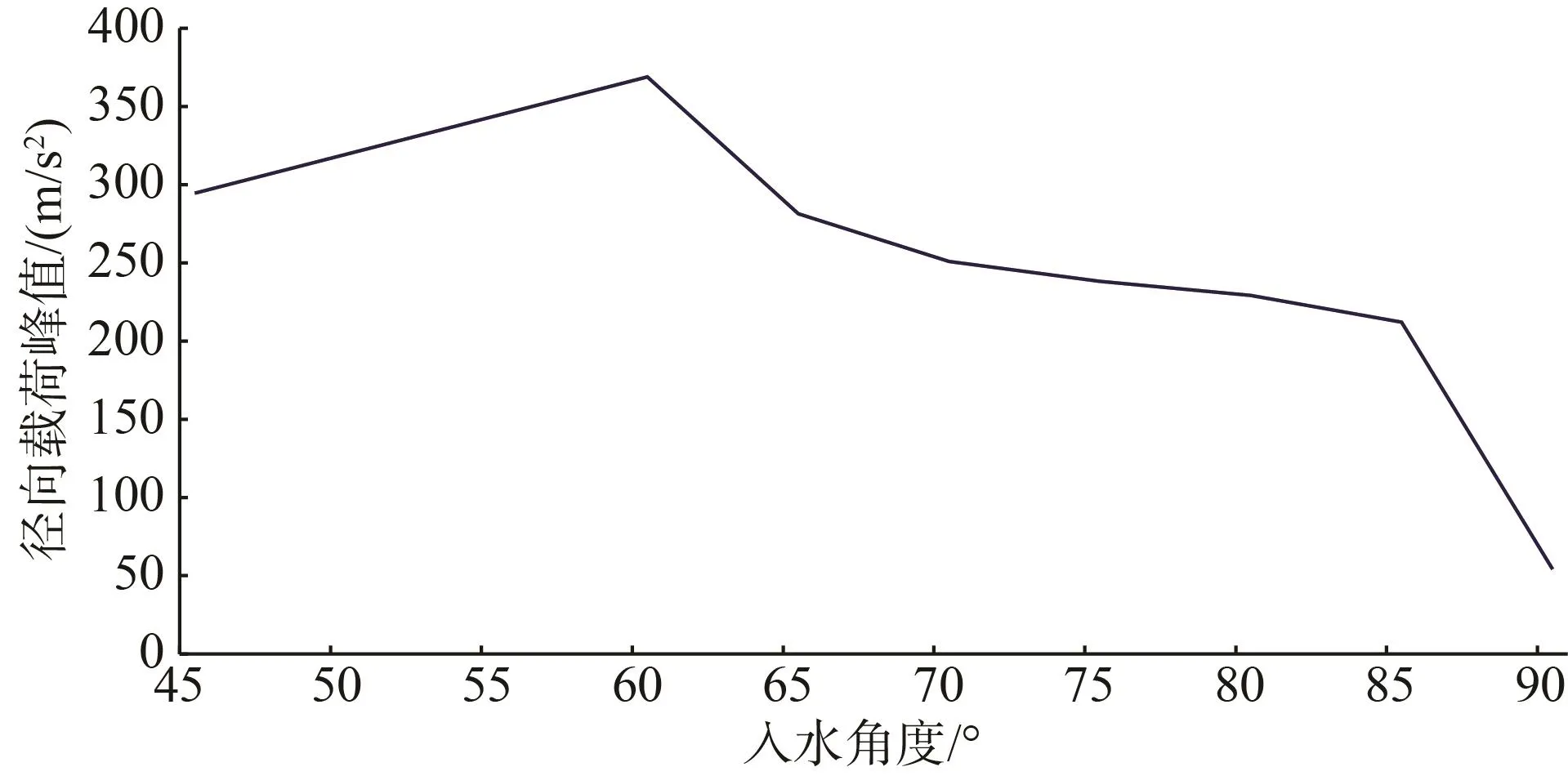
图10 航行器跨介质径向载荷峰值-跨介质角度曲线Fig.10 Cross-medium radial load peak-cross-medium angle curve diagram of UUV
由图9-10可以看出,航行器的轴向载荷峰值随跨介质角度的增大逐渐增大,在50 m/s的速度以不同的角度跨介质时,径向载荷峰值在跨介质角度60°时达到最大值。
由图11可以看出,航行器以50 m/s的速度不同的跨介质角度跨介质时,航行器受到的总的冲击载荷峰值随航行器的跨介质角度的增大而增大,在垂直工况下达到最大。对仿真数据点进行曲线拟合,得到拟合曲线:

图11 航行器跨介质总冲击载荷峰值-跨介质角度曲线Fig.11 Cross-medium total impact load peak-cross-medium angle curve diagram of UUV
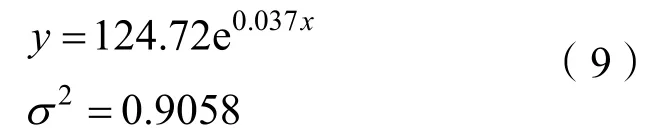
式中:y为航行器跨介质冲击载荷峰值;x为航行器的跨介质速度(45°~90°);2σ为曲线的拟合方差。
由拟合曲线的方程以及拟合方差可以看出,航行器以不同的角度跨介质时,航行器的跨介质载荷峰值与跨介质角度基本成指数函数的关系,航行器的跨介质冲击载荷峰值随航行器的跨介质角度的增大而增大。
由图8和图11可以看出,航行器的跨介质冲击载荷峰值随航行器跨介质工况的变化有以下几点规律:
1)在垂直跨介质时,航行器的跨介质冲击载荷峰值随着航行器的跨介质速度的增大而增大,并且跨介质速度与冲击载荷峰值基本成线性关系;
2)以相同的速度不同的角度跨介质时,随着航行器跨介质角度的增大,航行器轴向跨介质冲击载荷峰值增大;而径向跨介质冲击载荷峰值先增大再减小,在60°跨介质角时达到最大值;总冲击载荷峰值逐渐增大,并且冲击载荷峰值与航行器的跨介质角度基本成指数函数的关系。
4 结束语
本文基于所建立的航行器跨介质数值计算模型,对航行器跨介质过程中的动力学响应进行仿真研究,分析得到不同初始参数对航行器最大冲击载荷的影响规律。仿真结果表明,航行器的跨介质冲击载荷峰值随着航行器的跨介质速度的增大而线性增大,随跨介质角度的增加而指数增大。文中方法及结果可为航行器入水冲击过程的研究以及外形设计提供一定参考,但仍存在不足之处,如对该问题的机理分析研究不够深入,下一步需要从理论方面进行进一步研究。

