为孩子明天的发展而教

周春芝

【摘 要】一年级是学生数学学习的起始阶段，在平时的教学中，教师不仅要引导学生掌握相应的基础知识和基本的计算技能，同时还应注重引导学生体验基本的数学思想方法，发展学生的抽象和概括能力，提升学生的思维能力，不断落实核心素养的目标的达成。

【关键词】一年级数学 数学思想 数学模型 前瞻性

今年又执教一年级数学，同事调侃说：“一年级数学教师最轻松，基本上没事做。”问其何故，答曰：“现在孩子入学前，他们的父母基本上已教会其子女读、写100以内的数，口算20以内的加、减法，用竖式计算进位加法和退位减法的笔算。”这位同事说的是实情，可是我再从头至尾逐页研究苏教版数学一年级上册的教材时，发现同事刚才说的这些只是教学目标任务中的冰山一角，其实除了这些显性的基础知识和基本技能之外，还有诸如数学思想方法、数学活动经验、动手实践能力、思维能力、创新精神和意识等数学素养需要在平时的教学中逐步渗透和培养。现结合自己平时的教学工作，谈谈一年级数学教学的具体做法和体会。

一、抽丝剥茧，建立模型

数学课程标准指出：数学模型是学生体会和理解数学与外部世界联系的基本工具。它一端联系着现实生活中问题解决的对象，另一端指向一个去除非本质属性、纯化的数学知识结构。然而，由于我们长期对“数学模型”概念的曲解和片面认知，狭隘地认为“数学模型”是“高端”的方程、函数、图像等，一年级数学教学根本没有涉及数学模型思想的建立。张奠宙教授认为：“广义地讲，数学中各种基本概念和基本算法，都可以叫作数学模型。”加减乘除都有各自的现实原型，它们都是以各自相应的现实原型作为背景抽象出来的。每位数学教师从一年级开始引导学生经历把现实世界中有待解决或未解决的问题从数学的角度去发现问题、提出问题、理解问题，通过转化归结为一类已经解决或较易解决的问题，并综合运用所学的数学知识与技能求得结果的建模过程，让学生初步感受模型的简洁、高效、概括等特点，经历“生活—数学—生活”的探究之旅。                                                                                                                       在不断抽象、概括和建模，并运用模型解决问题的过程中，培养学生问题解决的能力。

案例一：

师（出示图1）：现在一共多少人？

生：一共是5人。

师：怎样得出是5人的。

生：我是数的。1，2，3，4，5。

师：可以从其他数开始数吗，还可以怎样数？

生：4，5。（指着后来的两个小朋友）

生：把原来的3人和后来的2人合起来就是5人。

师：你能用摆小棒的方法表示刚才合的过程吗？

（生操作，然后汇报交流）

生：先摆3根，再摆2根，合在一起就是5根。

师：先摆的3根表示什么？2根呢？5根呢？

生：表示原来的3个小朋友，再擺的2根表示后来的2个小朋友，5根表示合在一起一共有5个小朋友。

（板书：3     2     5）

师：像这样把3人和2人合起来是5人，可以用3+2=5来表示（顺势把板书补充完整），其中“+”就表示合起来的意思。

…………

师：3+2=5除了表示把3人和2人合起来是5人外，还可以表示生活中的哪些数学问题，你能举例说一说吗？

生：我原来有3支铅笔，妈妈又帮我买了2支铅笔，现在我一共有5支铅笔。

生：我先收了3本作业本，又收了2本作业本，一共收了5本作业本。

生：我先吃了3个苹果，然后又吃了2个苹果，一共吃了5个苹果。

…………

师：这里的3可以表示什么？2和5呢？

生：可以表示3个人、3支铅笔、3本作业本、3个苹果……

荷兰数学家弗赖登塔尔认为：学生学数学就是经历数学化的过程，也就是把数学研究的对象的某些特征进行抽象处理，用数学语言、图形或模型表达出来。上述案例中，学生从数出图中的总人数是5人，到用摆小棒的方法形象直观表征出自己的思维过程，直至最后从一类现实问题中抽象出数学加法算式并加以解释和应用，正是一个不断抽象、概括和建模的过程。学生完整经历了“生活—抽象—建模—应用”的探究之旅，体会到一个加法算式可以概括一类数学问题，这样的学习历程有助于积累学习经验，发展数学思考和数学思维能力，对提升学生的数学素养大有裨益。

二、细雨润物，渗透思想

小学数学教学内容包括两条线，一条是数学基础知识，这是一条明线，写在教材上，大家都能看明白;另一条是数学思想方法，这是一条暗线，并未直接写在教材上，而教学中又必须予以渗透、体验、感悟。数学教学中基础知识是重要的，数学思想方法同样重要。如果把数学基础知识看作外壳，那么数学思想方法就是内核。没有剥离具体数学基础知识的数学思想方法，也不存在撇开数学思想方法的数学基础知识。数学思想方法和数学基础知识是一个问题的两个面，相辅相成、互相促进。数学基础知识掌握得比较扎实，有利于数学思想方法的体悟;而数学思想方法的体悟又有利于对数学基础知识进行深层次的理解和建构。如果把数学学习比作一驾马车，那么数学基础知识和数学思想方法就是这驾马车的两个车轮，只有两个车轮同时发力才能驱动这驾“马车”奔向数学学科的殿堂。

案例二：

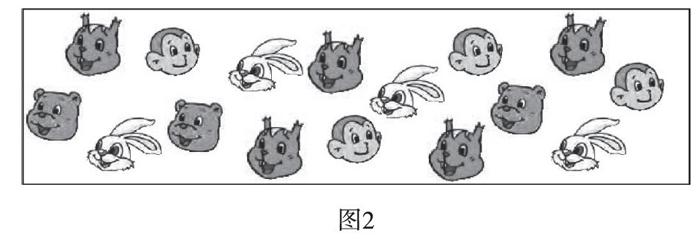
师（出示图2）：哪种小动物多？你会比一比吗？同桌之间可以合作，选取其中两种小动物比一比。

（汇报交流）

生1：小兔有4只，我们就摆4个圆片，小猴也有4只，我们再摆4个三角形。（如图3）

师：为什么要一个三角形对着一个圆片呢？这样做有什么好处？

生：可以很清楚看出小猴和小兔一样多。

师：通过一个三角形对着一个圆片摆，正好全部对完，我们可以看出小兔和小猴都没有多余的，我们就说小兔和小猴一样多。

…………

师：谁来说说你们是怎样比较小松鼠和小熊的。

生：我用花片代表小松鼠摆一排，同桌用正方形代表小熊也摆成一排，然后一个对着一个摆。（如图4）

生：小松鼠还有两只没有小熊对着。

师：我们就说小松鼠有多余的，小熊没有多余的。那么谁多谁少呢？

生：小松鼠比小熊多。

师：反过来怎么说，意思不变。

生：小熊比小松鼠少。

师：谁再来说一说小松鼠和小兔比是什么结果。（图略）

师：小松鼠有多余的，而小兔没有多余的，我们就说小松鼠比小兔多，或者说小兔比小松鼠少。

…………

上述案例中，学生自发地将同一类的小动物用同一种图形来代替，并摆成一排。其实这里的小动物排排队就是一种集合思想的体现。集合是数学中最基本的概念之一，把一组对象看作一个整体就形成一个集合（或集）。虽然教师没有为小朋友画上一个个集合圈，但是学生用自己的方式表达出了一个个集合。在比较的过程中采用“一对一”的方式摆放学具，已经无意识中运用了“一一对应”的数学思想方法帮助自己比较不同集合中元素个数的多与少。只不过有的是等价集合，如小兔和小猴的只数一样多;有的是非等价集合，如小松鼠比小熊多。现代数学教学论认为：掌握数学思想方法不但易于形成数学能力，而且对于提高学生的数学素质乃至科学素质、创新才能都有重大的作用。所以在平时的教学中，不仅要帮助学生解决“表面的知识”，更需要引领学生感悟这些闪烁着智慧光芒的数学思想和方法。

三、立足长远、放眼未来

“教学不应落后于发展”，数学教师不仅要了解“学生现在在哪里”，还要能预见“学生将来会到哪儿”。这就需要教师全盘了解小学数学知识的编排结构和体系，对本册、本年级、本学段教材，乃至1～6年级数学教材的内容都了然于胸。小学数学教材将四大领域分别编排在不同年级和不同学段的数学教材中，总体呈螺旋式上升、波浪式前进的态势。前后知识之间如筋骨相连，脉络清晰。教师在平时的教学中除了要教好当前的数学知识，更要为学生今后的学习与发展做长远考虑。一言以蔽之：我们的数学教学要求教师要有前瞻性，虽然学生懵然不知，但教师要有未雨绸缪的远见。

案例三：

师（出示图5）：先填一填，再观察这些算式中的数，你有什么发现？

生：加号前面的数都是从小到大排的，加号后面的数是从大到小排的。

师：你是怎样观察的？

生：我是從上往下观察的。

师：如果从下往上观察，你又有什么发现？

生：加号前面的数是从大到小排的，加号后面的数是从小到大排的。

师：不同的观察顺序就会得到不同的发现，还有什么发现吗？

生：从上往下看，加号前面的数每次增加1个，而加号后面的数每次减少1个。

师：为什么有这样的规律呢？同学们你能看一看左边的圆圈图，或者想一想刚才分圆片的过程说一说这样变化的原因吗？

生：我是看圆圈图，左边每次多涂1个圆圈，右边就会少1个白圆圈。

生：我是想刚才分圆片，每次从右边移一个圆片到左边，左边就会增加1个，右边的圆片就减少1个。

师：通过刚才看圆圈图和想分圆片的过程，我们知道了加号前面数变化会引起加号后面的数也跟着发生变化。再看一看，有什么是不变的？

生：加出来的得数都是10。

师：为什么得数不变呢？

生：因为不管怎样分，每行还是10个圆。

上述案例中，学生不仅掌握了10的拆分和加法，同时通过观察发现两个加数的变化规律，并且联系圆圈图和分圆片的过程揭示规律产生的原因，体会到一个加数变化会引起另一个加数跟着变化，但不变的是得数都是10。函数思想就是用运动和变化的观点去分析不同变量之间的关系。到了六年级，学生将要认识正比例和反比例函数。首先要理解什么是相关联的量，一个量发生变化能引起另一个量跟着变化，这样的一组两个量就是相关联的量，那个不变的量就是守恒量。以上教学过程为学生今后的学习进行了必要的渗透和铺垫，实现了从“静止”向“运动”的转变，从“常量”向“变量”的转变。

不积跬步何以致千里。假设一年级的数学学习是“起跑线”，而教师要做的就是引导学生在数学求知的道路上扎实、稳妥地走好每一步。在平时的教学实践中既要注重基本知识和基本技能的掌握，又要注重基本数学思想感悟和基本活动经验的积累，把数学核心素养悄然渗透在平时的点滴教学之中。