基于机器学习的时间反转散射体检测方法

韩令贺， 狄帮让， 胡自多， 刘威， 王国庆， 徐中华

1 中国石油大学(北京)油气资源与探测国家重点实验室， 北京 102249 2 中国石油勘探开发研究院西北分院， 兰州 730020 3 中国石油天然气集团有限公司油藏描述重点实验室， 兰州 730020

0 引言

传统地震勘探通常使用反射波信息估算地下介质的速度，并通过不同的偏移方法对地下连续反射层和地质构造进行成像(李振春，2014；陈生昌和周华敏，2016).虽然近年来速度建模和偏移方法的进步大大提高了地下地质体的成像精度(Wang and Tsvankin，2013; Fletcher et al.，2019)，但反射波勘探由于其本身的局限性，仍无法准确识别出地下的不连续地质体，如断层、尖灭点、溶洞、裂缝等小尺度散射体.而这些与地震主波长尺度相当或更小的局部构造和岩性信息对于提高地震勘探的分辨率具有重要意义，也有利于提高小尺度地质体的预测精度和钻探目标靶点选择的可靠性.

地下小尺度散射体的地震响应常表现为绕射波或散射波(绕射波即狭义上的散射波)，因此，绕射波成像成为检测地下散射体最常用的方法.在地震原始数据中，绕射波能量一般比反射波能量弱一到两个量级(Landa et al.,2008)，往往淹没在较强的反射波信号中，准确识别难度较大，而在常规资料处理(动校正、叠加)中，绕射波能量也会被压制.因此，绕射波成像首先要对绕射波和反射波进行较好的分离，再单独对绕射波进行偏移成像.国内外学者根据绕射波与反射波在运动学和动力学特征上的差异，在绕射波分离与成像方面提出了很多不同的方法：Landa等(1987)提出在共绕射点剖面上利用相关来增强绕射点位置的地震信号振幅，以检测地下局部非均匀地质体；Khaidukov等(2004)根据反射波和绕射波的聚焦特性不同，采用聚焦-反聚焦方法提取出主要包含绕射波信息的炮集并进行成像；Koren和Ravve(2010)则利用局部角度域成像构建全方位方向角道集，并通过镜像加权叠加和绕射加权叠加分别得到反映地下连续地质体和小尺度地质体的成像结果；朱生旺等(2013)利用局部倾角滤波和预测反演联合分离绕射波，可以提取出完整的绕射波信息.除此之外，还可以利用本征矢量法(Bansal and Imhof, 2005)、Radon方法(Nowak and Imhof,2004)、平面波分解(PWD)方法(黄建平等，2012)和多聚焦方法(Berkovitch et al., 2009)进行绕射波分离与成像.

地下小尺度散射体的物性参数通常与围岩有较大差异，在速度模型中表现为速度突变或速度异常区，对这些速度异常区的检测和定位是无损检测技术主要解决的问题.同时地下小尺度散射体也可以看作是绕射源，对小尺度散射体的检测和地球物理中广泛存在的震源定位问题有一定的相似性，如天然地震震源定位、微地震震源检测、火山震颤等.

近年来，时间反转原理逐渐被应用于震源定位问题，该原理基于无耗散介质中波动方程具有时间不变性和互易性的性质，通过将记录的波场数据时间反转、反向传播并聚焦到初始的震源位置.时间反转是一种基本的物理规律，具有物理可实现性.法国巴黎大学的Fink(1992)在超声学领域提出时间反转镜(TRM，Time Reverse Mirror)技术，并将其成功应用于粉碎肾结石的实验.随后，时间反转在水下声学、通信、无损检测、碎石术和癌症治疗等很多领域得到推广应用(Kuperman et al.,1998; Chakroun et al., 1995, Thomas and Fink, 1996).如果给定准确的地下介质模型，时间反转可以通过波动方程数值实现.在勘探地震学领域，时间反转原理主要用于被动源的震源定位.McMechan等(1985)提出可以利用波场反向外推进行震源分析，并利用该技术对1983年加州一次天然地震的震源进行了分析.Lu等(2008)利用时间反转原理定位微地震震源，以在开发过程中监控储层变化.Zhu(2014)对黏声介质的声波方程进行修改，利用时间反转原理实现了井间地震震源的定位.Lellouch 和Landa(2018)利用时间反转聚焦对井间地震数据进行速度建模.

对于被动源的震源定位，利用时间反转原理搜索模型中所有时刻反传波场的最大振幅值即可定位出震源位置及震源激发时刻.而对于主动源激发并由地下散射体产生的绕射波，由于绕射波能量相对于反射波能量较弱，同时由于散射体的多样性导致绕射波形态也较为复杂，因此，利用时间反转原理检测地下散射体的位置面临很多困难.本文通过分析主动源模型中反传波场在绕射点的聚焦状态，提取不同的特征反映波场聚焦的程度，并采用机器学习中的朴素贝叶斯分类算法计算出模型中每个点成为绕射点的概率，最终检测出地下散射体最有可能存在的位置.最后通过散射体模型和Sigsbee2a模型数据的试算，验证了本文方法的有效性和正确性.

1 时间反转原理

无耗散介质的声波方程可以写为

(1)

二维情况下，式(1)中P(x,z,t)为压力场，v(x,z,t)和ρ(x,z,t)分别为速度和密度.该方程中只包含了波场P对时间的二阶偏导数算子，具有时间不变性.如果P(x,z,t)是方程的一个解，那么P(x,z,-t)也是方程的一个解.考虑到时间的因果性关系，用P(x,z,T-t)表示方程的解，其中T表示记录的总时间，并假设该时间T足够长且P(t>T)=0.

时间反转原理基于无耗散介质中波动方程具有时间不变性和炮检互易性的性质，并具有物理可实现性.理想情况下的时间反转腔体实验由Fink在超声实验室完成，如图1所示.假设包围震源的封闭表面上分布着足够密集的传感器，可以接收压力场及其法向导数，根据惠更斯原理即可以计算出封闭表面内任一点的波场值.时间反转腔体实验包括两步，第一步：一个点状震源在封闭表面内激发出球面波，波前在经过非均匀介质时发生扭曲，并被封闭表面上的传感器接收，如图1左侧所示.第二步：将传感器接收到的信号沿时间方向反转，并从每个传感器将时间反转后的信号发出，波场将沿原路径返回，并最终在震源点位置聚焦，如图1右侧所示.

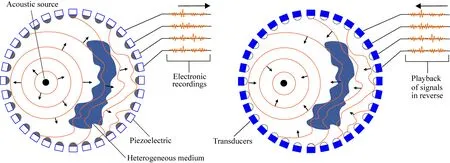
图1 时间反转腔体实验(Fink，1999)Fig.1 Time-reversal cavity experiment (Fink，1999)

时间反转腔体只是一种理想情况下的实验，实际地震勘探中只能在地表放置检波器，也无法观测到波场的法向导数.因此，实际应用中只能采用有限孔径的时间反转镜(TRM)来实现波场在震源点位置的聚焦，TRM可以是任意的形态和维度.医学和无损检测等领域的研究已证实，在非均匀介质中由于存在多次聚焦，TRM对震源点仍具有较好的聚焦能力(Fink,1999).

时间反转原理的数值实现在地震勘探中已得到应用，通常用于被动源的震源定位，其数值实现包括两步：(1)将检波点记录的地震数据沿时间方向反转；(2)将时间反转后的地震数据进行反向传播，反向传播通常采用波动方程有限差分法实现.时间反转也是逆时偏移的重要组成部分，逆时偏移在时间反转的基础上增加了两步：炮点波场的正向传播及成像条件的应用.成像条件通常选择炮点正传波场和检波点反传波场的零延迟互相关，但这两个波场在波阻抗反射界面上会产生较强的逆散射能量，经过互相关后会产生严重的低频噪声.同时，错误的子波估计也会导致逆时偏移的成像结果产生一些假象.

图2和图3是对被动源模型进行的时间反转试验，在图2a的两层介质模型中，被动源位于(1000 m,800 m)处，被动源可以是天然地震或微地震震源，地表接收到的单炮记录如图2b所示，记录长度为1.2 s，波场包含直达波和层界面产生的反射波，对此单炮记录进行时间反转，并采用声波方程高阶有限差分法进行反向传播，图3a—d为不同时刻的反传波场.可以看到，随着反传时间从1.2 s减小到0 s，反传波场在震源点位置逐渐聚焦，在t=0 s即震源激发时刻震源点位置的能量最强.因此，对于被动源的震源定位，利用时间反转原理搜索模型中所有时刻反传波场的最大振幅值即可定位出震源位置及震源激发时刻.

图2 被动源模型时间反转试验 (a) 速度模型； (b) 单炮记录.Fig.2 Time-reversal experiment of passive source (a) Velocity model； (b) One shot record.

图3 不同时刻反传波场快照 (a) 0.6 s； (b) 0.4 s； (c) 0.2 s； (d) 0 s.Fig.3 Back propagation wavefield snapshot at different times

图4和图5是对主动源模型进行的时间反转试验，实际地震勘探都采用人工震源，属于主动源模型.在图4a的均匀介质模型中有一个散(绕)射点，均匀介质的速度为2000 m·s-1,散射点的速度为4000 m·s-1.震源位于(1000 m,0 m)处，散射点位于(1000 m,800 m)处，检波点位于地表，记录长度为1.2 s，波场包含直达波和散射点产生的绕射波.由于绕射波能量一般相对于直达波小2个量级，相对于反射波小1个量级，因此反传时去掉直达波，去除直达波后的单炮记录如图4b所示.图5a—d为不同时刻的反传波场.可以看到，在不同时刻的反传波场呈现出不同的聚焦状态，在t=0.4 s即震源激发的波场到达散射点的时刻，反传波场恰好在散射点位置聚焦(此时散射点相当于二次震源)，在其他时刻反传波场呈现出非聚焦状态.因此，对于主动源模型，反传波场理论上应该在散射点的激发时间聚焦，但对于实际资料，速度不可能完全准确，无法准确计算出散射点的激发时刻，只能以某种方法判断反传波场的聚焦状态，达到检测地下散射体位置的目的.

图4 主动源模型时间反转试验 (a) 速度模型； (b) 去除直达波后的单炮记录.Fig.4 Time-reversal experiment of active source (a) Velocity model； (b) One shot record after removing direct wave.

图5 不同时刻反传波场快照 (a) 0.8 s； (b) 0.6 s； (c) 0.4 s； (d) 0.2 s.Fig.5 Back propagation wavefield snapshot at different times

2 时间反转散射体检测方法

实际地震勘探中人们关注的地下小尺度散射体可以看作是主动源模型中的散射点，根据时间反转原理，通过分析每个时刻反传波场的聚焦状态，可以判断模型中的每一个点是散射点还是非散射点，理论上可以检测出地下散射体的位置.我们需要计算模型中每个点的聚焦质量来评估其聚焦状态，对二维空间中任一点(x,z)和任一反传时刻t，需要计算在一个时空窗内的聚焦函数F(x,z,t)，聚焦函数的大小正比于该点成为散射点的概率.由于存在多次聚焦现象，波场会在不同的时刻在散射点聚焦多次，将所有时刻的聚焦函数累加得到每个点最终的聚焦函数，累加值越大，该点为散射点的概率越大，结果也越可靠.关于聚焦函数的选取可以借鉴图形图像处理方面的算法(Pertuz et al.,2013)，但对于地震反传波场，由于波场形态的复杂性和散射体的多样性，同时缺少准确的震源子波和模型速度信息，很难给出一个准确的聚焦函数分析波场的聚焦状态.

2.1 朴素贝叶斯分类算法原理

考虑到时间反转散射体检测需要对模型中任一点分析其反传波场的聚焦状态，从而判断该点是散射点还是非散射点，因此，这是一个典型的分类问题，更适合采用基于机器学习的分类算法.目前常用的分类算法包括朴素贝叶斯分类、决策树、支持向量机、逻辑回归、随机森林、K最近邻、人工神经网络和深度学习等算法，其中朴素贝叶斯分类算法具有算法简单、分类准确率高、速度快的优点，在工业界得到了广泛应用.

朴素贝叶斯分类是一种基于概率统计的分类方法，以贝叶斯定理为理论基础，并假设特征条件之间相互独立.该方法是一种监督学习方法，先通过已给定的训练数据，以特征条件之间独立作为前提假设，学习从输入到输出的概率密度函数，再将学习到的模型应用到新数据，输出新数据的分类结果.

假设有变量x和y，x表示特征变量，且x有n种取值，y表示分类变量，且y有m种取值，那么对于贝叶斯分类问题，根据贝叶斯公式和全概率公式，可通过式(2)计算出类别y的后验概率p(y|x)，即特征x属于y类的概率：

(2)

式中，p(x,yi)表示联合概率，p(yi)表示类别yi的先验概率，p(x|yi)表示似然函数，即特征x在类别yi下的条件概率，p(x)表示证据因子，对于给定的特征x，p(x)为固定值，且与类别y无关.

朴素贝叶斯分类基于贝叶斯定理并假设特征条件之间相互独立，则式(2)可改写为：

(3)

式(3)即为朴素贝叶斯分类器的表达式，对于训练样本来说，需要提取样本的特征属性，并计算先验概率p(yi)，即每个类别yi在训练样本中的出现频率，及每个特征属性对每个类别的条件概率p(xj|yi).

2.2 朴素贝叶斯分类实现过程

本文将朴素贝叶斯分类算法应用于时间反转散射体检测中，对模型中每个时刻每个点的反传波场进行分类，判断该点是散射点还是非散射点.根据对波场分类的任务特点，朴素贝叶斯分类算法的实现过程包括三大步：

2.2.1 数据准备阶段

根据分类任务的具体情况确定特征属性，对每个特征属性进行适当划分并分类，形成训练样本集合.这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定.

对于模型中每个时刻每个点的反传波场来说，特征属性应该能反映反传波场的聚焦特征，具有物理意义的特征属性能提高训练效果，本文对一个时空窗内的反传波场计算如下两种特征属性：

(1)聚焦点到时空窗中心的加权距离：

(4)

其中，f1(x,z,t)表示特征属性，w为模型中任一点的时空窗，时空窗的大小取为时间和空间域的平均波长，di=‖li-lcenter‖表示时空窗内任一点到中心点的距离，li表示将时空窗按像素点排列后第i个像素点，Ai为第i个像素点的振幅.如果聚焦点恰好位于时空窗的中心点，f1的值为最小.

(2)反传波场和高斯函数的相关系数：

(5)

其中，X、Y分别为时空窗的反传波场和高斯函数，cov(X,Y)表示两者的协方差，σX、σY分别为X、Y的方差.相关系数越大，表明时空窗内反传波场的形态和高斯函数的形态越接近，反传波场聚焦特征越好.

2.2.2 训练阶段

这一阶段主要工作是计算每个类别在训练样本中的出现频率及每个特征属性对每个类别的条件概率，输入是特征属性和训练样本，输出是分类器.本文采用高斯朴素贝叶斯分类方法，即假设每一类的数据都服从高斯分布，那么每一类的概率密度函数为：

p(xj|yi)=

(6)

其中，d为特征属性的维度，本文计算两种特征属性，因此d=2；μi为第i个类别所有特征的均值，Σ为协方差矩阵.

训练阶段通过式(6)计算每一类的高斯概率密度函数，即可得到每个特征属性对每个类别的条件概率，同时统计每个类别在训练样本中的出现频率，利用式(3)即可得到朴素贝叶斯分类器.

2.2.3 分类阶段

分类阶段输入新数据，并计算新数据的特征属性，利用训练阶段得到的朴素贝叶斯分类器对其进行分类.输入待分类的每炮数据的反传波场，输出每个反传时刻模型中每个点成为散射点的概率，因存在多次散射现象，将所有时刻所有炮的计算结果累加并进行归一化，最后得到模型中每个点成为散射点的概率.

图6为应用朴素贝叶斯分类进行时间反转散射体检测的算法框架图.在训练阶段需分别对无绕射波的反传波场和有绕射波的反传波场数据提取两种特征属性进行训练，生成朴素贝叶斯分类器，无绕射波的反传波场可由平滑速度模型和密度模型进行正演模拟得到，有绕射波的反传波场可由绕射源模型进行正演模拟得到；在分类阶段，输入实际数据、速度模型和密度模型即可利用分类器进行分类，计算模型中每个点成为散射点的概率.

图6 时间反转散射体检测算法框架Fig.6 Time-reversal scatterer detection algorithm framework

3 模型算例

3.1 简单散射点模型

设计如图7所示的模型，模型大小为100 m×100 m，网格间距为1 m，速度为常数700 m·s-1，密度模型为在常密度背景模型上设计了2个反射层和3个散射点，3个散射点分别位于(30 m，45 m)、(50 m，45 m)、(70 m，45 m).采用二维声波方程数值模拟方法计算得到20炮正演数据，采用的观测系统如下：检波点位于地表，从x=1 m到x=99 m每隔1 m放置一个检波点，每炮99道接收；炮点位于地表，从x=1 m到x=96 m每隔5 m放置一个炮点，共20炮，主频80 Hz，采样间隔1 ms，采样长度500 ms.正演的第11炮和第12炮数据如图8a所示，为减小绕射波和反射波的能量差异，对正演数据加增益(AGC, Automatic Gain Control)并添加高斯白噪后单炮如图8b所示.从单炮记录上可以识别出2个反射层的1次反射波及3个散射点的1次散射波，同时由于反射层界面上下较强的阻抗差异，导致单炮发育几套短周期多次反射波及多次散射波.本文的时间反转散射体检测方法不需对反射波和绕射波进行分离，只需对单炮数据加增益，使两者的能量处于同一量级即可.

图7 散射点密度模型Fig.7 Density of scatterer model

图8 正演炮记录 (a) 第11和12炮记录； (b) 加AGC和高斯白噪后炮记录.Fig.8 Forward modeling shot records (a) The 11th and 12th shot records； (b) Shot records after adding AGC and Gaussian white noise.

图9为采用图6所示的时间反转散射体检测方法对有绕射波和无绕射波的两类反传波场进行训练的结果，纵、横坐标分别为利用式(4)、(5)计算的两种特征属性，每类训练样本为100000个，其中红色圆圈代表有绕射波数据的训练结果，蓝色圆圈代表无绕射波数据的训练结果.从图中可以看到，两类数据的特征属性具有明显差异，有绕射波数据和高斯函数的相关系数较高，中心点加权距离较小；而无绕射波数据和高斯函数的相关系数较低，中心点加权距离较大.利用这两种特征属性可以对有绕射波数据和无绕射波数据进行较好的区分，经训练后产生的朴素贝叶斯分类器可用于对模型中的散射体和非散射体进行分类.

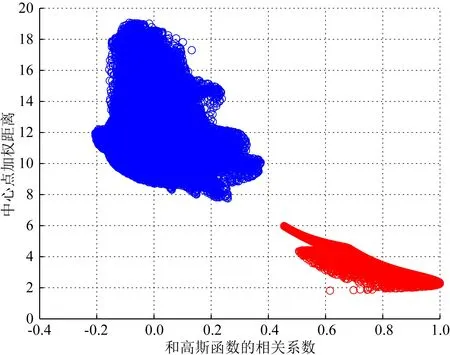
图9 两类训练数据特征属性的交会图 红色、蓝色圆圈分别代表有绕射波数据和无绕射波数据的训练结果.Fig.9 Crossplot of two kinds of training data feature attributes The red and blue circles represent the training results with and without diffraction data respectively.

应用本文方法对20炮正演数据进行试算，将所有时刻的结果累加可以得到每炮的散射体检测结果.对第11炮正演数据检测结果进行分析，图10为3个散射点处的检测概率随反传时间的分布图，可以看出，由于多次散射的存在，在几个不同时刻都会检测到散射体聚焦的现象，并且由于炮点位置的不同，不同散射体的聚焦次数也不同，对第11炮数据而言，左侧散射点检测到2次聚焦，中间散射点检测到1次聚焦，右侧散射点检测到4次聚焦，但t=0.25 s处的检测概率很小，在对所有时刻的结果累加时会选择一个门槛值，将较小的概率检测结果剔除，并用聚焦次数对累加结果进行归一化，得到每炮最终的检测结果.图11a为第11炮数据的散射体检测结果，对20炮数据的散射体检测结果进行累加，并以总炮数进行归一化，得到最终的散射体检测结果，如图11b所示.从最终的散射体检测结果中可以看出，在3个散射点位置都能检测到较大的概率，非散射点位置的检测概率相对很小，检测结果能较好的反映散射点的位置.

图10 散射点位置检测概率随反传时间的分布 (a) 左侧散射点(30 m，45 m)； (b) 中间散射点(50 m,45 m)； (c) 右侧散射点(70 m,45 m).Fig.10 Distribution of detection probability of scattering point location with back propagation time (a) Left scatterer (30 m，45 m)； (b) Middle scatterer (50 m，45 m)； (c) Right scatterer (70 m，45 m).

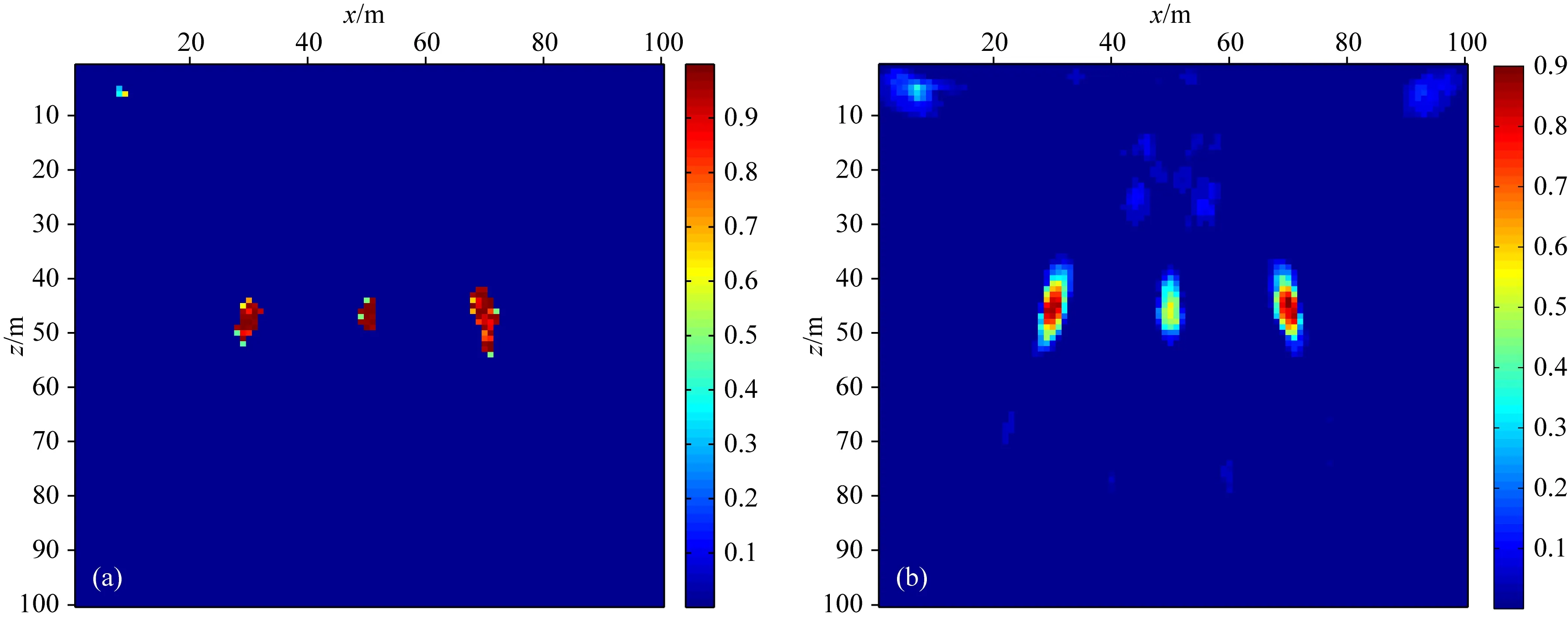
图11 散射体检测结果 (a) 第11炮数据； (b) 20炮数据.Fig.11 Scatterer detection results (a) The 11th shot； (b) 20 shots.

3.2 多个散射体模型

为检验本文算法对地下散射体的纵横向分辨能力，设计如图12所示的多个散射体模型，模型大小为2000 m×1400 m，纵横向网格间距均为10 m.模型从上至下三层介质的速度分别为2500 m·s-1、3000 m·s-1、4000 m·s-1,在第2层介质中分布有12个纵横向不同间距的高速散射体，散射体的大小均为10 m×10 m、速度为4500 m·s-1.第1和第2个散射体与第1层反射界面重叠，第3和第4个散射体的纵向距离为100 m，第5和第6个散射体的横向距离为100 m，第7和第8个散射体的纵向距离为50 m，第9和第10个散射体的纵向距离为20 m，第11和第12个散射体的横向距离为50 m.设计观测系统如下：检波点位于地表，每个网格点均放置一个检波点，每炮201道接收；炮点位于地表，从第2个网格点，每隔6个网格放置一个炮点，共34炮，主频30 Hz，采样间隔1 ms，采样长度1400 ms.采用声波方程数值模拟方法进行正演，将正演数据的直达波切除并加增益作为本文算法的输入，其中第16炮数据如图13所示，从正演单炮中可以看到两层的反射波及散射体产生的大量绕射波.应用本文方法对34炮正演数据进行试算，将所有时刻的结果累加可以得到每炮的散射体检测结果，将每炮检测结果累加并进行归一化后得到最终的散射体检测结果，如图14所示.从检测结果中可以发现，对于第1和第2个散射体，虽然两者和第1层反射界面重叠在一起，输入数据也没有将反射波和绕射波分离，但本文算法不受反射层的影响，仍能清楚地检测到散射体的位置，这对于塔里木盆地检测某些和反射层位置重叠的溶洞等散射体具有重要的参考价值.

图12 多个散射体模型Fig.12 Multiple scatterer model

图13 多个散射体模型正演单炮Fig.13 One forward modeling shot of multiple scatterer model

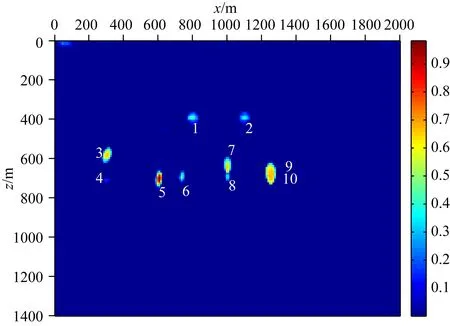
图14 34炮数据的散射体检测结果Fig.14 Scatterer detection result of 34 shots

该模型也可以验证本文方法在检测散射体时的纵横向分辨率.第2层介质的速度为3000 m·s-1，震源主频为30 Hz，因此第2层内震源子波的波长为100 m.第3和第4个散射体的纵向距离为1个波长，第7和第8个散射体的纵向距离为半个波长，从检测结果上可以看到，第3和第4个散射体、第7和第8个散射体都能区分开，只是由于下方散射体产生的绕射波在向上传播时会受到上方散射体的影响，所以下方散射体的检测概率要小于上方散射体；第9和第10个散射体的纵向距离为20 m，小于1/4个波长，两个散射体的检测结果相互重叠为一个检测概率较大的散射体，因此两个散射体不能被有效区分开.

从检测结果中可以看到，第11和第12个散射体的横向距离为50 m，两个散射体无法被检测到，究其原因，笔者认为这与算法选取的时空窗大小有关，由于时空窗的大小至少要包括整个地震子波的长度，因此时空窗的大小通常选取为1个波长.当两个散射体的横向距离小于或等于半个波长时，两个散射体的绕射波相互叠合导致在1个时空窗内的聚焦特征较差，被检测到的概率较小.当两个散射体的横向距离大于半个波长时，才能被检测到并有效区分开，如第5和第6个散射体的横向距离为100 m，两者均可以被清晰地检测到.

3.3 Sigsbee2a模型

为验证本文算法对复杂构造的适用性，选取部分Sigsbee2a模型进行测试，速度模型如图15所示，模型中下部含有两个高速散射体.模型大小为276×226个网格点，纵横向网格间距均为15.24 m.设计观测系统如下：检波点位于地表，每个网格点均放置一个检波点，每炮276道接收；炮点位于地表，从第15个网格点，每隔20个网格放置一个炮点，共13炮，主频20 Hz，采样间隔2 ms，采样长度4000 ms.采用声波方程数值模拟方法进行正演，将正演数据的直达波切除并加增益作为本文算法的输入，其中第7炮数据如图16所示.应用本文算法对13炮正演数据进行试算，将每炮检测结果累加并进行归一化后得到最终的散射体检测结果，如图17所示.可以看到，检测结果在模型下部的两个高速散射体位置能得到较大的概率，同时检测结果对于模型3条断裂中速度突变的断点位置也能得到较好的反映，将检测到的断点位置用红色虚线连接起来得到断裂检测结果如图18所示，和模型中的3条断裂具有较高的吻合度.同时由于断点位置的速度突变弱于散射体位置，断点产生的绕射波能量也弱于散射体产生的绕射波能量，因此，断点位置的检测概率也小于散射体的检测概率.

图15 部分Sigsbee2a速度模型Fig.15 Partial Sigsbee2a velocity model

图16 Sigsbee2a模型正演单炮Fig.16 One forward modeling shot of Sigsbee2a model

图17 13炮数据的散射体检测结果Fig.17 Scatterer detection result of 13 shots

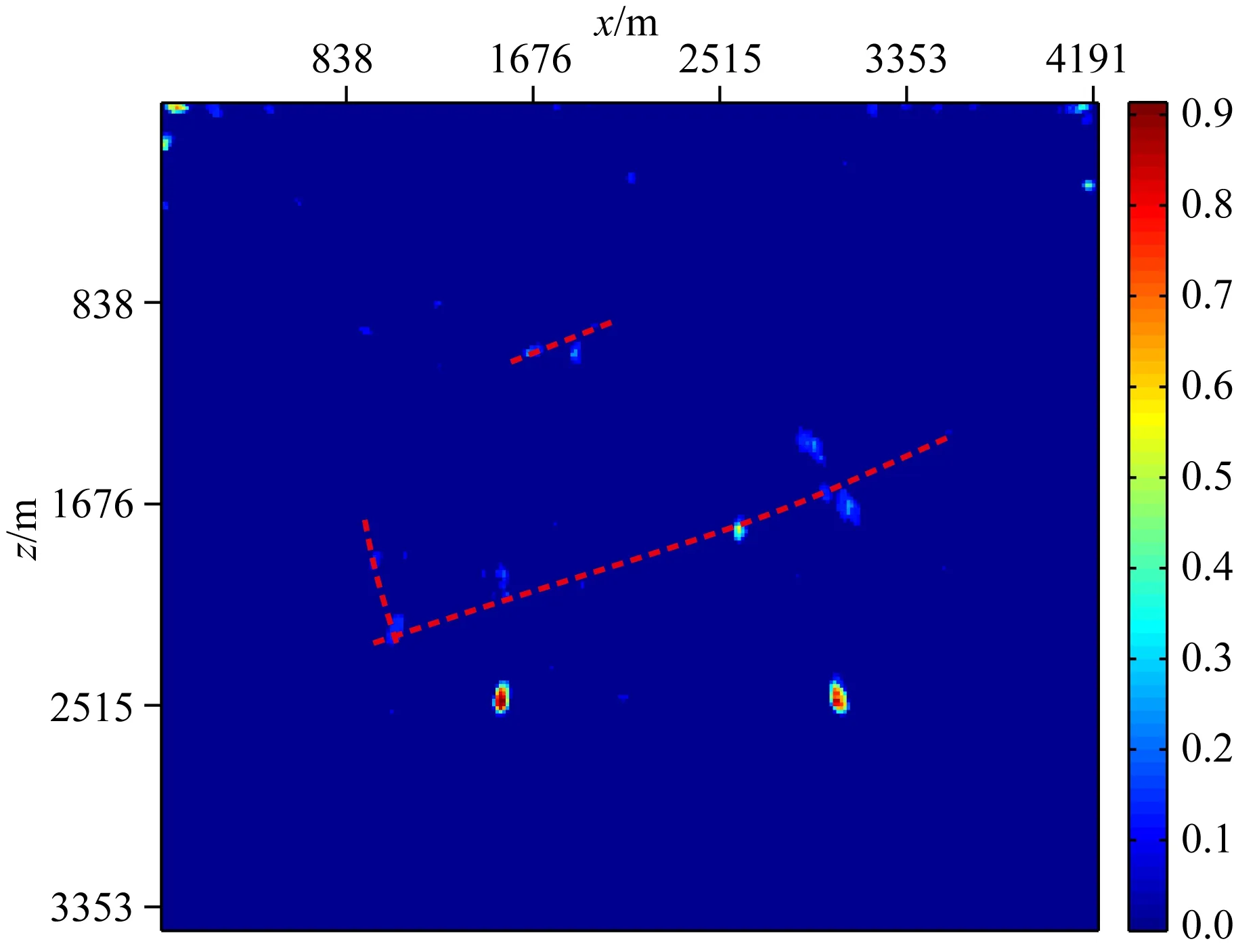
图18 断裂检测结果Fig.18 Fracture detection result

4 结论与讨论

时间反转原理基于无耗散介质中波动方程具有时间不变性和互易性的性质，已被广泛应用于被动源震源定位问题，同时也是逆时偏移的重要组成部分.本文将时间反转原理引入到地下散射体检测和定位中，并针对地下反传波场形态的复杂性和散射体的多样性，引入机器学习中的朴素贝叶斯分类算法，计算两种反映波场聚焦状态的特征属性，给出适用于时间反转散射体检测的分类算法框架，计算得到模型中每个点成为散射体的概率，最终检测出地下散射体最有可能存在的位置.散射体模型和Sigsbee2a模型的试算结果表明，本文方法在不需对反射波和绕射波分离的情况下，即可实现对地下散射体的检测和定位，即使散射体和反射层重叠在一起也不受反射层的影响，同时由于考虑了多次散射的影响，检测结果能准确反映地下散射体的位置.利用多个散射体模型对本文方法的纵横向分辨能力进行了探讨，结果表明受选取时空窗大小的影响，本文方法检测散射体的纵向分辨率要大于横向分辨率.

训练样本的质量对朴素贝叶斯分类算法的效果具有重要影响，本文给出的时间反转散射体检测方法流程中，对于有绕射波的训练样本假定散射体是点源形态，实际地下散射体的形态比较多样，在后续研究中利用多种散射体产生有绕射波的训练样本，可能会提高朴素贝叶斯分类算法的分类效果.同时，对于三维情况下的散射体检测，如何提取能反映三维反传波场聚焦状态的特征属性是一个较大的挑战，也是作者后续的研究重点.