GRACE/GRACE-FO空窗期的陆地水储量变化数据间断补偿：以全球典型流域为例

2021-09-06 12:09:46徐鹏飞蒋涛章传银芮明胜刘宇

地球物理学报 2021年9期

徐鹏飞，蒋涛，章传银，芮明胜，刘宇

1 中国测绘科学研究院，北京 100830 2 山东科技大学测绘与空间信息学院，山东青岛 266590

0 引言

陆地水是不可或缺的重要自然资源，与人类活动密切相关，由于水资源的分布不均，制约着国家和地区的高速发展，严重影响我国可持续发展战略(Zhong et al.，2009).因此，陆地水储量异常TWSA(Terrestrial Water Storage Anomaly)的长期可持续监测，对于研究水循环过程，合理配置水资源，预防洪涝、干旱等自然灾害等有相当重要的科学意义和参考价值(Chen et al.，2009).

2002年初，GRACE(Gravity Recovery and Climate Experiment)卫星开始运行，基于GRACE获取空间中长尺度的时变重力场信息，可反演TWSA，使TWSA的长期可持续监测成为可能，国内外学者基于GRACE数据对区域TWSA进行了大量研究(Tapley et al.，2004；Yeh et al.，2006；Tiwari et al.，2009；Chen et al.，2014；Long et al.，2016).直至2017年10月，GRACE任务结束，CSR(Center for Space Research)、GFZ(Helmholtz-Centre Potsdam-German Research Centre for Geosciences)、JPL(Jet Propulsion Laboratory)三所机构最新发布的GRACE Level-2 RL06(Release 06)数据更新至2017年6月，但由于卫星后期运行存在的质量问题，一般2016年8月之后的数据不再使用.2018年5月，为延续GRACE任务，GRACE-FO(GRACE Follow-On)成功发射升空，该卫星将继续监测全球重力场的变化.近期CSR、GFZ、JPL公布了最新的GRACE-FO Level-2 RL06球谐系数数据，下文简称GRACE-FO SH，截至2021年1月10日，数据的时间段为2018年6月至2020年11月，由此GRACE与GRACE-FO之间存在了20多个月的数据空窗期.为得到长期连续的TWSA监测结果，更准确的研究TWSA的年际变化与长期趋势特征，从而合理利用配置水资源，一种有效的针对GRACE/GRACE-FO数据空窗期的TWSA间断补偿方法是十分必要的.

数据间断的补偿可通过时间序列分析或机器学习等方法预测实现，国内外学者针对水储量变化的预测开展了大量研究工作.Mirzavand和Ghazavi(2015)利用ARMA(Autoregressive Moving Average)、ARIMA(Autoregressive Integrated Moving Average)、SARIMA(Seasonal Autoregressive Integrated Moving Average)对伊朗喀山平原的地下水位进行预测试验，研究表明可提前60个月对地下水位取得较好的预测效果.Adamowski和Chan(2011)利用小波神经网络WNN(Wavelet Neural Network)预测加拿大魁北克的地下水位，并与ARIMA方法比较，验证了该方法的有效性及潜力.Dos Santos和Pereira Filho(2014)利用ANN(Artificial Neural Network)，并引入天气变量，预测圣保罗地区的用水需求，发现天气对用水消耗存在反馈作用.另外还有WA-ANN(Wavelet Analysis-Artificial Neural Network)、SVR(Support Vector Regression)等其他方法(Adeli and Jiang，2006；Moosavi et al.，2013；王宇谱等，2013；Tiwari and Adamowski，2015；Al-Zahrani and Abo-Monasar，2015；Mukherjee and Ramachandran，2018).传统的时间序列分析方法实现简单，基于最小二乘原理构造随时间变化的函数，向后递推，从而预测后续序列.然而该方法对于信号成分复杂的时间序列的预测效果较差，且易受到信号中噪声成分的影响，从而预测失真.相较而言，ANN、WA-ANN、SVR算法的精度较高，但需额外的物理变量进行约束(如气象数据等)，实现困难，计算效率较低.综上所述，本文将引入奇异谱分析SSA(Singular Spectrum Analysis)+ARMA组合方法(Shen et al.，2018；牛余朋等，2020)，预测GRACE/GRACE-FO空窗期的TWSA，从而对TWSA的间断进行补偿.GRACE运行多年，积累了较为充足的样本，且近期GRACE-FO数据的发布，为间断补偿的精度评定提供了可靠依据.

SSA作为一种时间序列信号的处理方法，在GNSS(Global Navigation Satellite System)数据处理等领域应用较多(王解先等，2013；Kondrashov and Berloff，2015；肖胜红等，2016)，但在水储量变化的预测方面应用较少，从有限时间序列的动态重构出发，结合特征向量分析(Eigenvector Analysis)，SSA方法可充分识别并提取信号中不同成分(如周期、趋势、噪声等)，且无需引入额外的物理变量，实现较为简易，特别适合分析预测具有周期特征的TWSA时间序列.Li等(2019)利用SSA方法预测了中国多个地区的水储量变化，取得了较好的效果，但关于如何选择训练样本、检验样本提高预测模型精度的讨论尚不充分.因此，本文将选取TWSA周期特征明显的全球典型流域为例，验证SSA方法在典型流域的适用性及间断补偿效果，并进一步讨论如何选择训练样本、检验样本构建更适用于间断补偿的预测模型，从而提高GRACE/GRACE-FO数据空窗期TWSA间断补偿结果的精度.此外，虽然SSA方法可以有效对TWSA序列的周期项等主要成分进行分解与重构，但剩余随机序列中依然存在部分有效信息，而剩余随机序列可以利用ARMA模型进行拟合递推.为此，本文引入了SSA+ARMA组合方法进一步提高间断补偿结果的精度.从全球选取亚马逊流域、多瑙河流域、恒河流域、密西西比河流域、尼日尔河流域、伏尔加河流域、叶尼塞河流域、长江流域这八个典型流域进行试验，并分别利用SSA+ARMA、SSA、ARMA和WNN算法进行对比分析，验证SSA+ARMA方法的适用性和有效性.后续采用GRACE-FO SH反演TWSA、Mascons、GLDAS(Global Land Data Assimilation System)数据，评定基于SSA+ARMA方法的TWSA间断补偿结果精度，验证方法的可靠性.

1 数据

1.1 GRACE/GRACE-FO level-2 RL06

本文使用CSR的GRACE/GRACE-FO RL06 大地水准面球谐模型GSM(Geoid Spherical Harmonic Model)球谐系数文件，阶数为60阶，下文简称GRACE SH.选取GRACE SH的时间段为：2003年1月—2016年8月，共计149个月数据(部分月数据缺失).截至2021年1月10日，新发布的GRACE-FO SH时间段为：2018年6月—2020年11月，共计28个月数据(2018年8月、2018年9月数据缺失).与RL05数据一样，这些数据扣除了固体潮汐、海洋潮汐、非潮汐的大气和海洋信号(Bettadpur，2003).与RL05相比，RL06数据在参数选择、算法设计、数据编辑、背景场模型构建等方面进行了优化，“条带”误差与截断误差有明显的改善(Save，2018；Göttl et al.，2018).数据预处理阶段分别用SLR(Satellite Laser Ranging)提供的C20项和来自Swenson的一阶项，替换GSM中的C20项、一阶项(Swenson and Wahr，2002；Cheng and Tapley，2004).此外，冰川均衡调整(GIA)引起的重力场长期变化趋势利用了三维压缩地表负荷滞弹响应模型进行扣除(Geruo et al.，2013).

1.2 Mascons结果

为验证GRACE SH反演TWSA的可靠性及对间断补偿结果进行精度评定，本文选取JPL、CSR、GFZ的Mascons RL05以及JPL、CSR的Mascons RL06数据进行比较.Mascons RL05数据的分辨率为1°×1°，每月一值，数据时间段为2003年1月至2017年1月.JPL发布的Mascons RL06数据的分辨率为0.5°×0.5°，每月一值.CSR发布的Mascons RL06数据的分辨率为0.25°×0.25°，每月一值.截至2021年1月10日，基于GRACE-FO数据的Mascons RL06结果已经更新至2020年10月.经过泄漏误差的修复、GIA改正等一系列处理后，具有更好的精度，因此广泛应用于GRACE SH反演TWSA结果精度的验证分析(Scanlon et al.，2016).其中Mascons RL05采用的GIA改正模型为三维压缩地表负荷滞弹响应模型，与本文对GRACE SH的处理一致.而Mascons RL06采用的ICE6G-D模型(Purcell et al.，2016).二者模型存在差异，但差异主要体现在南极地区，在本文所选的研究流域中差异较小(马超等，2016).

1.3 GLDAS水文模型

本文选用GLDAS V2.1的NOAH模型，时间段为2003年1月—2020年2月，其分辨率为0.25°×0.25°.该模型考虑了0～200 cm的土壤水、植物冠层地表水、雪水当量，不包含地下水部分.本文将利用GLDAS数据求解单尺度因子，一定程度上修复球谐系数滤波引起的泄漏误差，以及验证补偿结果的可靠性.

2 原理及方法

2.1 GRACE SH反演TWSA方法

GRACE SH可反演流域内等效水高EWH(Equivalent Water Height)变化，然而GRACE重力场模型中存在高阶噪声及“条带”误差，因此本文引入了半径300 km的FAN滤波和P3M15的去相关滤波的组合滤波方法，从而反演得到八个典型流域的TWSA，具体公式如下(Wahr et al.，1998； Han et al.，2005；Zhang et al.，2009；詹金刚等，2011)：

×[ΔCn mcos(mλ)+ΔSn msin(mλ)]

(1)

2.2 SSA原理

SSA本质是针对一维时间序列的主成分分析方法，对于X=(x1,x2,…,xN)，SSA方法时间序列分析过程主要分为分解与重构两个方面，具体过程如下(Vautard et al.，1992；Chen et al.，2013)：

(1)轨迹矩阵

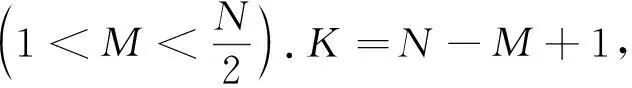
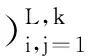
(2)

式中Xi=(xi,…,xi+M-1)T(1≤i≤K).X为M×K阶轨迹矩阵.

(2)奇异值分解

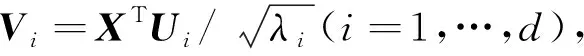
X=X1+X2+…+Xd,

(3)

(3)分组

将d个初等矩阵分成m个互不相交的子集I1,I2,…,Im，设I={i1,i2,…,ip}，则对应于子集I的合成矩阵可表示为：

XI=Xi1+Xi2+…+Xip,

(4)

将矩阵X以合成矩阵形式表示为：

X=XI1+XI2+…+XIm,

(5)

因此，分组的过程即是对I1,I2,…,Im的确定过程.

(4)时间序列重构

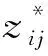
(6)

重构成分能够反映时间序列的变化特征，各重构成分功率谱密度的相对关系可用于有效信号提取与信噪分离.

2.3 SSA迭代预测方法与SSA+ARMA方法

本文采用的SSA迭代预测算法由SSA迭代插值法发展而来，二者的原理是一样的(Schoellhamer，2001；Beckers and Rixen，2003；Kondrashov et al.，2010；郭金运等，2018).将GRACE SH反演的TWSA时间序列作为训练样本，通过SSA分解对时间序列进行重构.迭代预测的具体步骤如下：

(1)设定预测时长n，将n个0值加到训练样本(长度为N)的末尾处，构建总长度为N+n的新序列.

(2)对长度为N+n的新序列进行SSA分解，将第一个重构成分(RC1)末尾处的n个值替换新序列，作为预测数据.之后循环该过程，最终前后两次SSA分解的RC1之间的残差小于阈值，根据经验阈值取0.01 mm(Shen et al.，2018；周茂盛等，2018).

(3)当步骤(2)循环过程结束时，继续通过SSA分解添加RC2，通过线性叠加RC1和RC2末尾处的n个预测值构建新序列，循环该过程直至前后两次分解的RC1+RC2之间的差值小于阈值.

(4)重复上述过程，直至用K个RC线性叠加(RC1+RC2+…+RCk)末尾处的n个预测值，且满足阈值条件，则序列末尾n个值即为TWSA的预测值.

以预测时序与检验样本符合精度最高为准则，结合W-correlation(Weighted Correlation)及FFT(Fast Fourier Transform)方法进行有效性和适用性检验(见3.2节)，测试最佳窗口长度M和重构阶数K，并以此窗口长度M与重构阶数K，可以得到基于SSA方法TWSA预测结果.同时RC1+RC2+…+RCk的前N个值为与训练样本对应的SSA重构序列，将训练样本扣除SSA重构序列后得到剩余随机序列，建立ARMA(p，q)对剩余序列进行外推预测，SSA预测结果与ARMA外推结果之和为SSA+ARMA的间断补偿结果，此为SSA+ARMA方法(Shen et al.，2018；牛余朋等，2020).

2.4 精度评定指标

RMSE(Root Mean Square Error)：

(7)

RMSE数值越小，表示模拟值序列与观测值序列的误差越小，精度越高.

3 结果分析

3.1 GRACE SH反演TWSA与Mascons比较

为方便表述，本文以相关代号表示各流域——亚马逊流域(AZRB)、多瑙河流域(DNRB)、恒河流域(GNRB)、密西西比河流域(MSRB)、尼日尔河流域(NGRB)、伏尔加河流域(VGRB)、叶尼塞河流域(YNSRB)、长江流域(YZRB).八个流域边界范围如图1所示，数据来自HydroSHEDS数据集(https:∥hydrosheds.org/page/overview).

首先利用CSR提供的2003年1月—2016年8月的GRACE RL06 SH反演各流域的TWSA序列.其中有15个月的球谐系数数据缺失，需对其进行插值补全.传统方法为利用前后两年或多年该月份球谐系数的均值代替，而本文将采用SSA迭代插值方法对TWSA结果进行插值补全(Shen et al.，2018；周茂盛等，2018).以MSRB为例，结果如图2所示，图中为传统的前后两年球谐系数均值替代法与SSA迭代插值方法的对比，可以看出SSA方法的插值结果更符合周期变化的特征，这有利于后续SSA方法的周期分解与重构.而传统方法有明显的跳变，引入了较大的误差，特别2012年10月二者结果的差值达6.53 cm.为此，本文将采用SSA迭代插值方法对GRACE SH反演TWSA和Mascons结果的缺失数据补全.

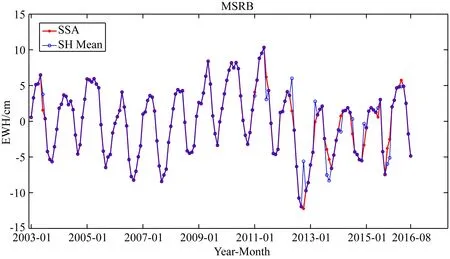
图2 基于SSA方法与SH平均方法的TWSA插值结果Fig.2 The interpolation results of TWSA using SSA and SH Mean

前文已知，本文采用组合滤波方法来抑制噪声和“条带”误差，但也造成了信号幅值的减小，空间分布衰减，即泄漏误差.为了恢复相对真实的TWSA，本文采用基于GLDAS数据的单尺度因子法，修复泄漏误差，该方法将GLDAS格网数据球谐展开并截取至60阶，采用与GRACE相同的处理流程得到区域TWSA序列，基于最小二乘原理求解TWSA时间序列与该区域原始GLDAS时间序列的比例系数(冯伟等，2012).由表1可知，不同流域的尺度因子存在差异，将研究流域GRACE SH反演的TWSA序列乘以对应的尺度因子，作为最终的反演结果.为验证GRACE SH反演TWSA结果的准确性和可靠性，本文将八个典型流域的TWSA分别与三所机构的Mascons RL05和JPL、CSR的Mascons RL06结果进行比较.

表1 不同研究区域的单尺度因子Table 1 Single scale factor in different study areas

如图3所示，GRACE SH反演的TWSA结果与Mascons结果相比，无论是振幅还是周期相位均有较强的一致性，这表明二者结果吻合性良好，验证了本文GRACE SH反演TWSA结果的有效性和可靠性，且三所机构不同版本间的Mascons结果差异也不明显.八个流域TWSA序列均有一定的周期信号特征，其中AZRB、NGRB(图3a，e)的TWSA序列周期特征最为明显，规律性更强，而DNRB、MSRB、YZRB(图3b，d，h)的信号成分复杂、周期特征相对较弱，序列中蕴含了更多的频率信息.

图3 GRACE SH反演研究区域的TWSA与Mascons结果比较Fig.3 Comparison of TWSA derived from GRACE SH with Mascons in study areas

本文通过计算八个流域的RMSE(cm)、NSE、R，定量评价GRACE SH反演TWSA结果与Mascons结果的符合精度.表2可知，GRACE SH反演TWSA结果与Mascons结果有较高的符合精度，大多数流域的RMSE在2 cm以内，且NSE、R在0.95以上.其中在AZRB、NGRB的符合精度最高，NSE、R都达到了0.99，RMSE也在1.5 cm之内.由NSE可知，在MSRB中，GRACE SH反演的TWSA与Mascons结果有较明显的差异，特别是RL06的Mascons结果.综合考虑，CSR的Mascons RL05、Mascons RL06结果与GRACE SH反演结果吻合程度最高，这与本文选取CSR的GRACE SH数据反演TWSA有关.由于Mascons RL05数据的时间范围所限，后续将采用CSR的Mascons RL06数据与TWSA间断补偿结果对比验证.

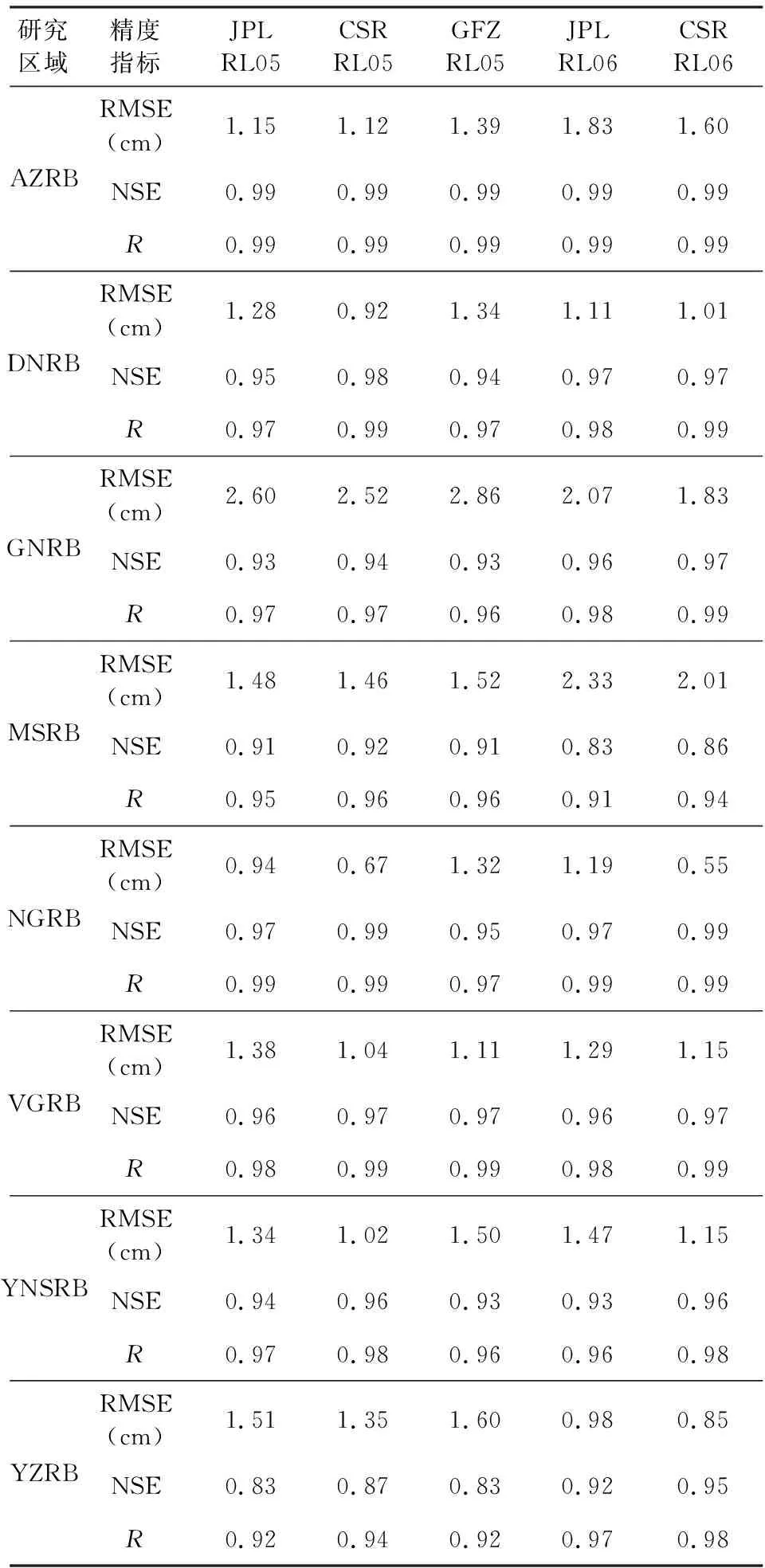
表2 GRACE SH反演研究区域的TWSA的精度评定Table 2 Accuracy assessment of regional TWSA derived from GRACE SH

3.2 SSA方法可行性分析

前文已知，在利用SSA方法预测前，需确定最佳窗口长度M和重构阶数K，本文以周期特征明显的AZRB的TWSA为例，详细说明该过程.为此将2003年1月至2012年12月的GRACE SH反演TWSA结果作为训练样本，共计120个数据.根据经验，GRACE SH反演的TWSA结果中可能存在3个月周期信号，因此在SSA分解时，将窗口长度M设置为3的倍数，连续测试窗口长度M，从而对分解的重构成分进行周期对分离.以预测时序与检验样本(2013年1月至2016年8月数据)符合精度最高为准则，不断测试，确定AZRB区域的最佳窗口长度M为48，重构阶数K为8.为定量描述各重构成分之间的相关性，检验模型的有效性和适用性，本文采用W-correlation进行分析，结果如图4所示，图4a可知，前8阶的两两相邻的重构成分相关系数均高于0.71，故前8阶重构成分中，相邻的两个阶项可能为周期对(如RC1与RC2、RC3与RC4、RC5与RC6等均具有相同的周期).图4b中，前8阶特征值的贡献率达98.29%.

图4 TWSA时序SSA分解RCs的 W-correlation分析结果Fig.4 W-correlation analysis of the RCs of TWSA with SSA

本文采用FFT方法探测各重构成分的周期特征，将具有相同周期信号特征的重构成分进行分组(Kay and Marple，1981).图5左侧为相邻两个RC之和的重构序列，右侧为该序列的功率谱密度.由图可知，RC1+RC2为具有年周期特征的信号，且其功率谱密度最大，对TWSA序列的贡献率最高，其振幅为：-21.92至22.35 cm；RC3+RC4为具有36个月周期特征的信号；RC5+RC6为具有18个月周期特征信号；RC7+RC8为具有6个月周期特征信号.因此本文选取前8阶重构成分对AZRB区域2003年1月至2012年12月的TWSA序列进行重构是适用的.

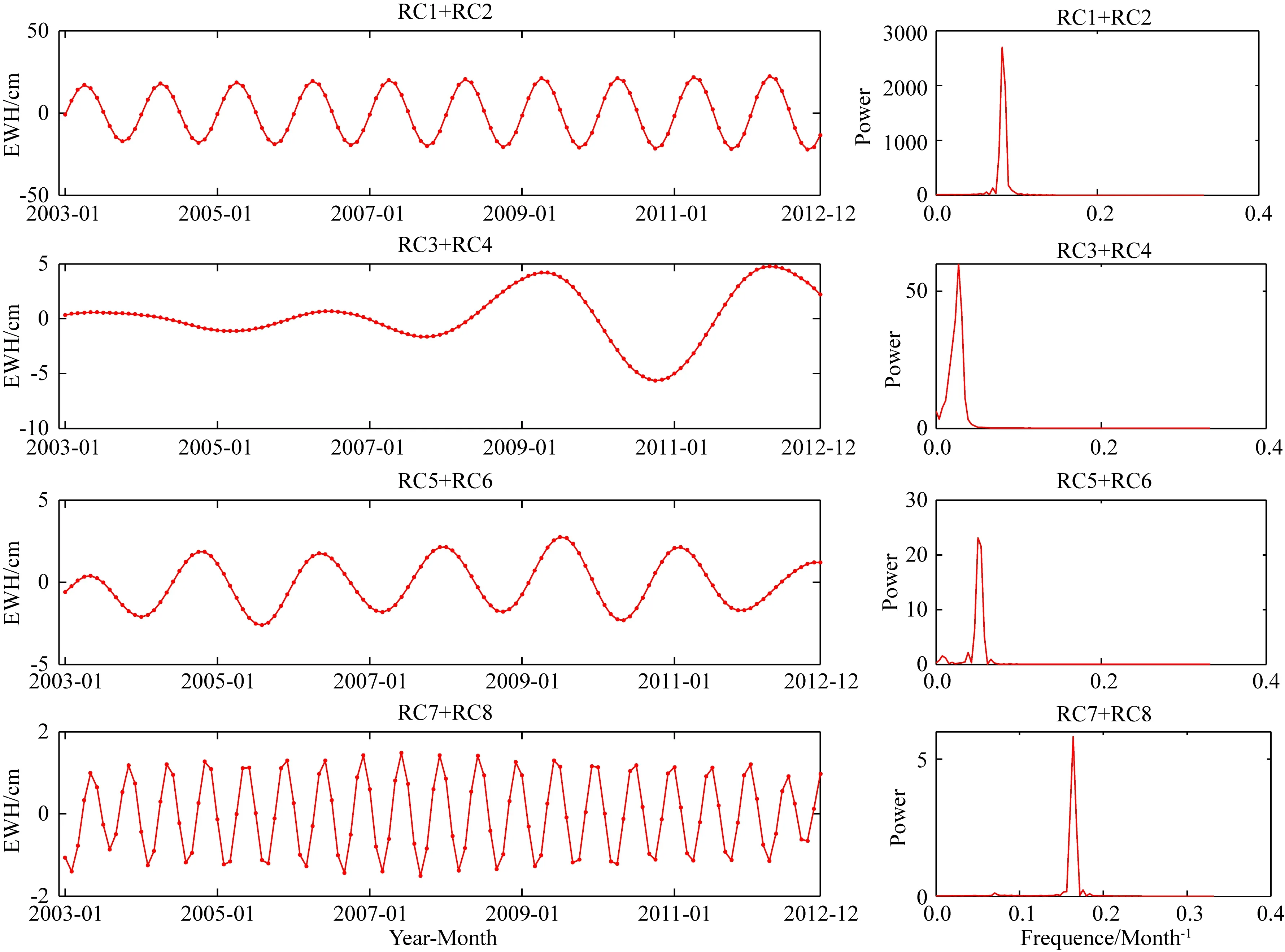
图5 TWSA时序SSA分解RCs的FFT周期探测结果Fig.5 FFT period detection results of the RCs of TWSA with SSA

如图6所示，将训练样本TWSA序列与SSA重构序列进行对比，两种结果吻合很好，特别是在周期相位上有很强的一致性，残差振幅也在2 cm左右，其符合精度分别为RMSE=1.71 cm、NSE=0.99、R=0.99.表明窗口长度M为48、重构阶数K为8的重构模型在AZRB是有效的，利用该重构模型继续生成新的序列，即SSA的预测值，验证了SSA迭代预测方法的可行性.同时，图6中残差序列即为SSA+ARMA方法中的剩余随机序列，利用ARMA模型对其进行外推，并与SSA方法的预测值相加，即为SSA+ARMA的间断补偿结果.不同流域的SSA预测模型窗口长度M和重构阶数K存在差异，根据以上过程最终确定各流域的SSA预测模型参数详见表4的预测模型A.

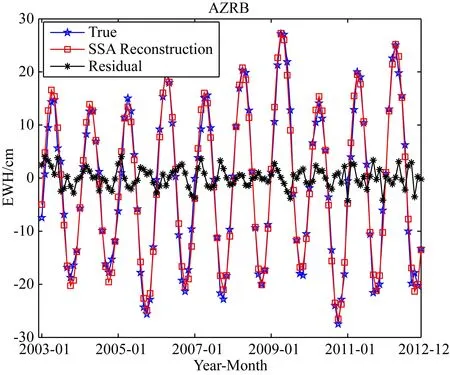
图6 AZRB区域TWSA序列与其SSA重构序列结果对比Fig.6 Comparison of SSA reconstruction results with TWSA in AZRB

3.3 ARMA预测模型有效性检验

同样以AZRB流域2003年1月至2012年12月的TWSA序列为样本，描述预测模型ARMA(p，q)的构建过程.首先对TWSA时间序列进行零均值处理，因为ARMA方法主要针对的是平稳时间序列，所以本文采用了ADF(Augmented Dickey-Fuller)检验对TWSA时间序列的平稳性进行检测，若序列不满足平稳性要求则需要进行差分处理，直至序列平稳(Luo et al.，2012；Mirzavand and Ghazavi，2015；牛余朋等，2020).利用AIC(Akaike Information Criterion)准则确定p、q，之后基于最小二乘原理求解模型的未知参数.构建模型后，还需有效性检验，有效性检验标准为拟合样本序列提取后的残差序列应与白噪声相似.本文在AZRB流域所构建ARMA(6，8)模型的有效性检验结果如图7所示.图7a为反映拟合序列与样本序列偏差的残差序列，振幅在-5.06 cm至7.02 cm之间.图7b为残差序列的正态QQ(Quantile-Quantile)图，残差的数值均分布在红线附近，且该残差序列满足显著性水平为0.05的Lilliefors假设检验，因而具有近似正态分布的特征.图7c、图7d中横轴表示滞后阶数，纵轴表示相关系数大小，当滞后阶数大于1时，残差序列的自相关函数、偏自相关函数数值很小，均在随机区间之内，且不随滞后阶数增大而下降，具有独立无关的随机特性.综上，残差序列为服从近似正态分布的独立无关随机变量，满足白噪声特性，所以AZRB流域构建的ARMA(6，8)是有效的，可以用于预测.

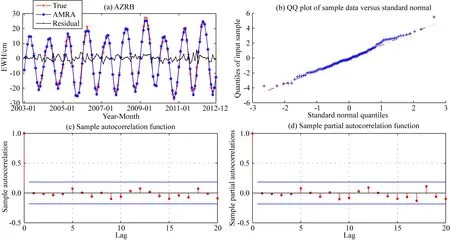
图7 AZRB区域ARMA(6，8)模型检验结果Fig.7 Test results of the ARMA(6,8) model in AZRB

不同流域的ARMA(p，q)模型存在差别，本文对不同流域的参数p、q进行测试，并进行有效性检验，最终确定了八个流域的ARMA模型：AZRB采用ARMA(6，8)，DNRB采用ARMA(7，6)，GNRB采用ARMA(6，7)，MSRB采用ARMA(8，8)，NGRB采用ARMA(9，8)，VGRB采用ARMA(8，8)，YNSRB采用ARMA(10，10)，YZRB采用ARMA(9，10).在SSA+ARMA方法中，各流域剩余随机序列的信号成分已发生变化，ARMA模型需要重新确定.

3.4 不同方法的TWSA预测结果比较

为比较SSA方法在典型流域的适用性，将前期120个月(2003年1月至2012年12月)的GRACE SH反演TWSA结果作为训练样本，分别用SSA+ARMA、SSA、ARMA与WNN方法预测后续44个月(2013年1月至2016年8月)的TWSA(Chen et al.，2006).并以同期的GRACE SH反演TWSA作为真值检验，评估不同方法的预测效果，从而选择适用于预测TWSA的方法.

如表3所示，四种方法TWSA预测序列均与真值序列有一定程度的吻合，但不同方法、不同流域之间还存在差异.SSA与SSA+ARMA方法的预测值与真值的吻合效果最好，且二者相差不大，ARMA方法效果最差.八个流域中，NGRB的TWSA预测结果精度是最高的，而DNRB、MSRB、YZRB预测结果精度相对较差.NGRB的TWSA时间序列的周期特征明显，规律性强，因而四种方法的预测结果均与真值时间序列吻合得较好.相反，DNRB、MSRB、YZRB地区的TWSA序列更加复杂多变，蕴含更多的信息，因而预测结果与真值序列符合相对较差.综合考虑三种精度指标，SSA与SSA+ARMA方法的预测精度较高且相对稳定，除AZRB外，其他多数流域的RMSE在4 cm以内，所有流域的NSE值在0.7以上，R值在0.85以上.WNN方法预测结果也有较高的精度，在DNRB、VGRB流域的预测精度还略优于SSA和SSA+ARMA方法，但在MSRB、YNSRB、YZRB预测精度较低，构建的预测模型适用性较差.相较而言，除在NGRB外，ARMA模型的预测精度最差，特别是在YZRB中，ARMA模型预测结果的NSE只有0.46.

表3 基于不同方法的TWSA预测精度评定Table 3 Evaluation of TWSA′s prediction accuracy based on different methods

图8为四种方法不同时段的预测精度，对多数流域来说，随预测时间与训练样本时间间隔越来越大，四种方法的预测精度逐渐下降，前两年的预测精度优于后两年的预测精度.不同时段中，SSA与SSA+ARMA方法在各流域均有较高的预测精度，且受预测时间长度逐渐增加的影响较小，特别是在YNSRB和YZRB中，2016年SSA+ARMA方法的RMSE分别为2.72 cm和1.59 cm，明显优于ARMA与WNN方法.ARMA方法预测精度较差，且受预测时间长度的影响较大，2016年AZRB的RMSE达到了14.25 cm.在MSRB、YNSRB、YZRB中，WNN方法2016年的预测精度较差，而AZRB、MSRB中，2016年的预测精度较高.大部分流域中所有时段SSA+ARMA方法的预测精度均略优于SSA方法，但二者差异较小.

图8 不同方法的TWSA预测结果对比Fig.8 Comparison of TWSA prediction results by different methods

综上所述，ARMA方法对于周期特征较弱的时间序列预测效果并不理想，易受到序列中噪声成分的干扰，导致预测结果精度降低.WNN方法为机器学习方法，通过不断调试学习速率、隐含层节点数等参数构建预测模型，计算效率较低，且因为缺少相关约束，某些流域构建的预测模型并不适用.在后续的研究中，若引入降水等气象数据作为约束，WNN方法构建模型的效率及预测精度可能会进一步提升，同样具有很大的潜力.而结合特征向量分析，SSA方法可有效识别并提取时间序列中不同成分，受噪声的影响小，能从复杂的信号成分中提取更多有用信息，特别适合分析预测具有复杂成分或信号周期特征明显的TWSA时间序列.

由表3可知，SSA与SSA+ARMA方法相比，SSA+ARMA方法要略优于SSA方法，且主要反映在RMSE上，其精度有0.01至0.1 cm量级的提升.这主要与各流域SSA重构序列的重构阶数有关，如图4b和图6所示，AZRB的前8阶重构成分的贡献率达98.29%，因此剩余时间序列包含的信息较少，精度提升并不明显.但各流域的SSA预测模型存在差异，对于SSA重构序列贡献率较低的流域，SSA+ARMA方法会有较明显的提升，如GNRB的重构阶数K为4(表4中预测模型A)，因而SSA重构成分的贡献率会较低，与SSA方法相比，其RMSE降低了0.35 cm，NSE、R均提升了0.2.

3.5 SSA+ARMA方法的预测模型构建及补偿结果精度评定

SSA+ARMA方法的预测精度主要还是由SSA方法的预测精度影响的.因而本文将讨论如何选择训练样本、检验样本构建更适用的SSA预测模型，提高GRACE/GRACE-FO数据空窗期TWSA补偿结果的精度.在之前的预测试验中，SSA迭代预测方法构建的各流域预测模型如表4中预测模型A所示，但该模型存在一定的局限性，训练样本选取的2003年1月至2012年12月的120个样本，并未充分考虑全部164个样本，且训练样本与GRACE/GRACE-FO间断期的时间跨度较大.因此构建的预测模型并不一定适用于数据间断的补偿.GRACE-FO数据作为GRACE的延续，本文对二者的数据处理过程一致，因此本文将GRACE-FO SH反演TWSA结果看作真值.为确定更准确、更适用于GRACE/GRACE-FO空窗期TWSA间断补偿的SSA模型，本文引入GRACE-FO SH反演TWSA及Mascons RL06结果作为检验样本，提出了另外两种构建预测模型的方案，三种方案区别如图9.预测模型A与预测模型B和C相比，分析了训练样本对预测模型构建的影响，其中预测模型B和C充分考虑了164个训练样本.预测模型B和C的区别在于检验样本的选择，上文已知，随预测时间与训练样本时间间隔越来越大，预测精度逐渐下降.因而预测模型B引入GRACE-FO SH反演TWSA结果作为检验样本，对间断补偿结果序列的末尾进行约束，从而得到更适用于间断补偿的预测模型.相较而言，预测模型C除了引入GRACE-FO SH反演TWSA结果，同时还考虑了Mascons RL06结果，可以对间断补偿结果序列的首尾两端均进行约束.以预测序列与检验样本符合精度最高为准则，确定了各流域的预测模型A、B、C的参数，即窗口长度M和重构阶数K.如表4所示，多数流域依据不同方案构建的SSA预测模型参数存在差异，特别是重构阶数K，在预测模型B和C中，AZRB的K为4，表示该流域SSA的重构序列中有4个重构成分，因而剩余随机序列中会包含较多的有效信息，相反NGRB的K为12，SSA方法对该流域TWSA序列的分解与重构更加充分，剩余随机序列中包含的有效信息较少.在VGRB、YZRB中，方案二和方案三构建的预测模型B与C是一样的.

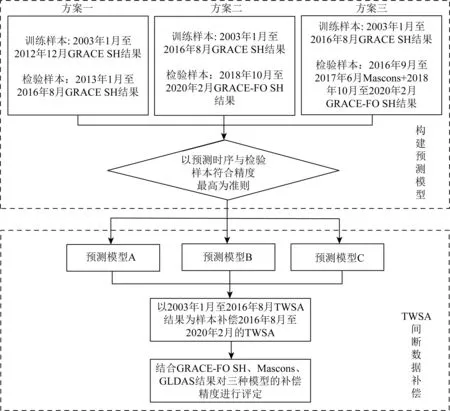
图9 三种方案的流程图Fig.9 Flow chart of the three programmes

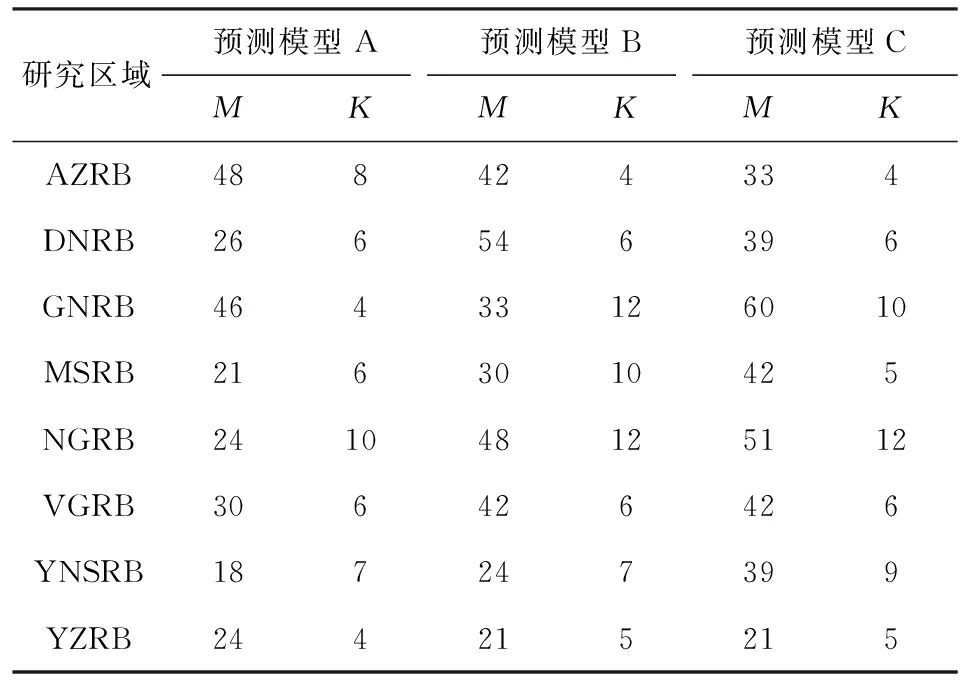
表4 基于不同方案的SSA预测模型Table 4 Prediction models of SSA based on different programmes

本文将GRACE SH反演的2003年1月至2016年8月TWSA序列作为样本，基于SSA方法分别采用预测模型A、B、C，补偿2016年9月至2020年2月的TWSA间断结果.为检验补偿结果的准确性及可靠性，受限于数据的包含范围，本文选取2016年9月至2017年6月的CSR的Mascons RL06结果，2016年9月至2020年2月的GLDAS结果，2018年10月至2020年2月的GRACE-FO SH反演TWSA结果进行对比验证.其中，GLDAS结果为对下载的格网序列球谐展开并截取至60阶后，进行与GRACE数据一样的处理流程后的结果.同样的，各类数据均扣除了对应数据2003年1月至2016年8月的均值，其中CSR提供的GRACE-FO RL06 SH扣除了该机构GRACE RL06 SH的2003年1月至2016年8月均值.三种方案在间断数据补偿阶段是一样的，均采用2003年1月至2016年8月的164个TWSA结果为样本，GRACE-FO SH结果与Mascons结果未参与实际预测过程，因此依据GRACE-FO SH结果与Mascons结果评定补偿结果精度是有意义的.

图10可知，除YZRB中预测模型A的补偿结果外，其他间断补偿结果均取得了较好的效果.基于SSA方法的TWSA间断补偿结果与Mascons、GRACE-FO SH结果吻合得较好，这验证了补偿结果的可靠性.表5中RMSE可知，TWSA间断补偿结果与GLDAS结果在振幅上有明显的差异，但由R可知，GLDAS结果与TWSA间断补偿结果在周期和相位变化上有较强的一致性，这亦能反映间断补偿结果的可靠性.振幅的偏差相对较大是因为GLDAS中只包含了0～200 cm土壤水、植物冠层地表水、积雪的变化，不包含地下水变化，而GRACE则反映了陆地总储水量的变化和固体地球可能的物理迁移(Chao，2016).因而在后续主要依据GRACE-FO SH反演的TWSA及Mascons结果进行精度评定.

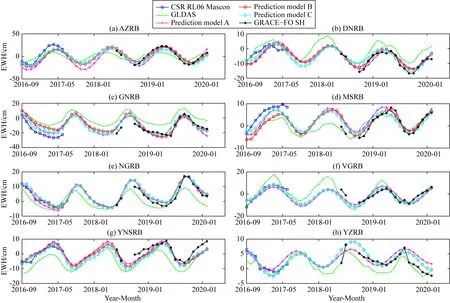
图10 基于SSA方法TWSA间断补偿结果与GRACE-FO SH，Mascons和GLDAS结果的比较Fig.10 Comparison of TWSA gap compensation results by SSA with GRACE-FO SH，Mascons and GLDAS results

表5可知，各流域中预测模型A、B、C的间断补偿结果精度存在差异.预测模型A的符合精度相对较差，表明在构建预测模型过程中，采用更充足的训练样本有利于构建更适用的预测模型.预测模型B、C均取得了较好的预测效果，但在细节上存在差异，预测模型B与GRACE-FO SH结果的符合精度最高，但可能会导致间断补偿结果序列的前部分失真，如DNRB的间断补偿结果与Mascons结果的NSE仅为-0.02；在GNRB中RMSE达10.60 cm.相较而言，预测模型C对间断补偿结果的首尾两端均进行了约束，不会出现这种问题.但值得注意的是，在MSRB中，比较NSE可得，预测模型B的补偿结果要优于预测模型C.这与本文GRACE SH反演的TWSA在该流域与Mascons结果存在较大差异有关(见表2).因此当引入Mascons RL06结果作为检验样本约束间断补偿结果时，反而会降低补偿精度.本文采用的GRACE/GRACE-FO SH均为CSR提供的RL06版本，且进行了相同的数据处理流程，可以看为同种数据，相反作为成熟产品的Mascons结果无法保证这一点.因而当预测模型B、C的补偿结果符合精度相当时，本文优先考虑预测模型B间断补偿结果.综上所述，AZRB、DNRB、GNRB、NGRB采用预测模型C的SSA间断补偿结果，MSRB、YNSRB采用预测模型B的SSA间断补偿结果，在VGRB、YZRB构建的预测模型B与C是一样的.

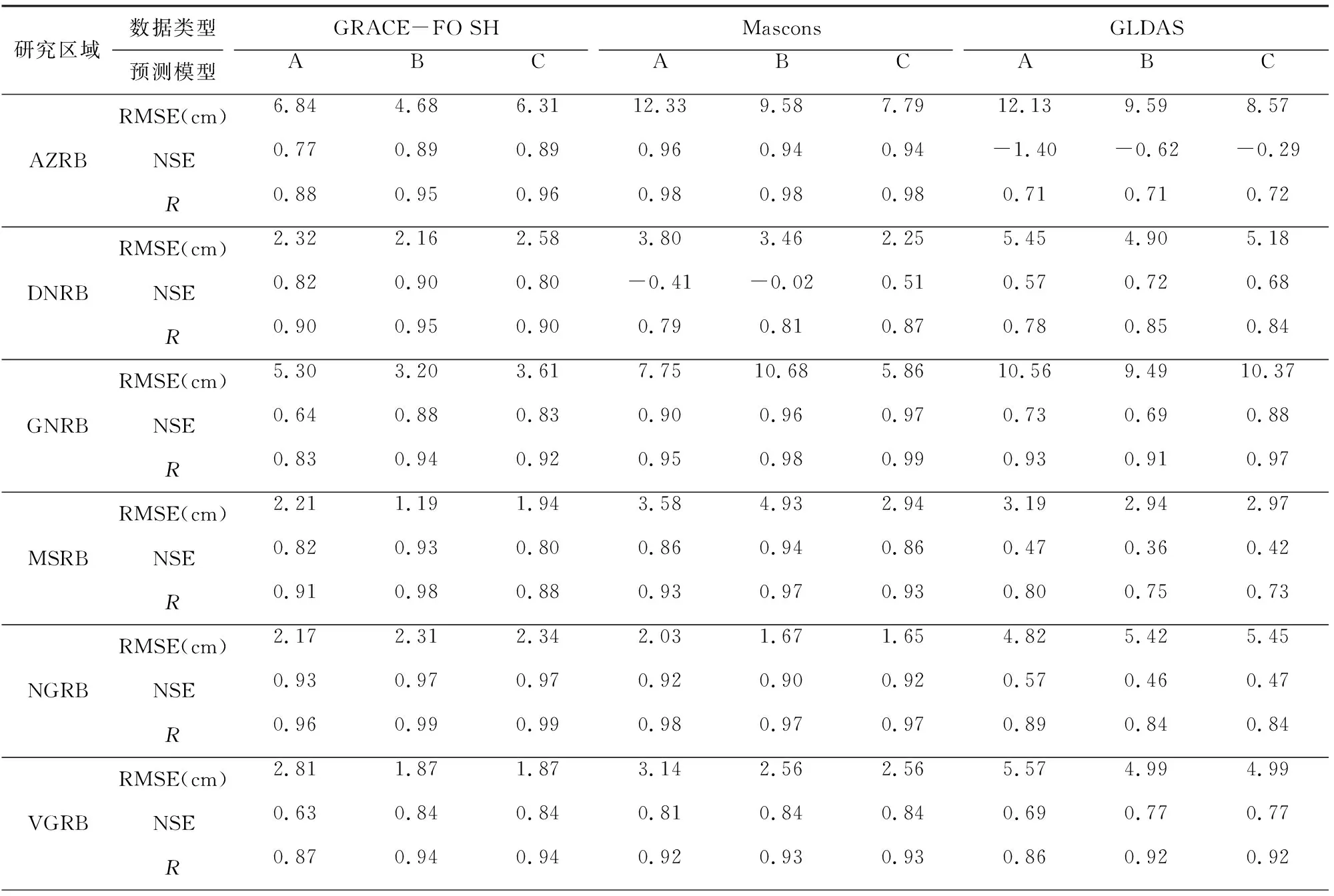
表5 基于SSA方法的TWSA间断补偿结果精度评定Table 5 Accuracy assessment of TWSA gap compensation results by SSA

续表5

根据上文选取的基于SSA方法的间断补偿结果，本文进一步采用SSA+ARMA方法提升补偿精度.表6可得，SSA+ARMA方法的间断补偿结果整体优于SSA方法，且主要体现在RMSE上.其中AZRB的间断补偿结果的精度提升最为明显，基于GRACE-FO SH结果的精度评定中，RMSE降低了1.35 cm，基于Mascons结果的精度评定中，RMSE降低了1.01 cm.除AZRB外，DNRB、NGRB、VGRB、YZRB的预测精度也有相对明显的提升.

表6 基于SSA+ARMA方法的TWSA间断补偿结果精度评定Table 6 Accuracy assessment of TWSA gap compensation results by SSA+ARMA

综上所述，基于SSA+ARMA方法的TWSA间断补偿结果有较高的精度，与同期GRACE-FO SH结果相比，除AZRB的RMSE为4.96 cm外，其他流域的RMSE均在4 cm以内；除YZRB的NSE、R分别为0.61、0.80外，其他流域的NSE值均在0.80以上，R值均在0.90以上.对TWSA序列相对复杂多变的DNRB、YZRB(图3b，h)，间断补偿结果也取得了较好的效果，特别是YZRB(图10h)的2018年10月—2019年7月周期特征不明显，而SSA间断补偿结果与GRACE-FO SH结果却有很强的一致性，这充分体现了SSA方法能识别、提取复杂成分信号中有用信息的特性.在八个典型流域中，NGRB的间断补偿结果精度最高，这可能与该流域受人类活动影响少，TWSA序列具有强周期特征有关.

3.6 基于SSA+ARMA方法的TWSA间断补偿结果试验

上文三种方案的预测模型构建中，由于部分流域GRACE SH反演的TWSA与Mascon结果符合较差，因而预测模型B和C互有优势.但在实际应用中，若采用同种数据作为训练样本与检验样本，方案三构建的预测模型取得的间断补偿效果更好.截至2021年1月，基于GRACE-FO的CRS RL06 Mascon数据结果已经更新至2020年10月，对基于SSA+ARMA方法的TWSA间断补偿的实际应用提供了充足的数据支持.

本文采用方案三的预测模型构建思路，利用2003年1月至2016年8月的Mascon结果为训练样本，2016年9月至2017年6月及2018年10月至2020年2月的Mascon结果作为检验样本构建SSA预测模型.构建预测模型后，在实际应用中为得到精度更高的间断补偿结果，无需考虑精度评定的问题，间断补偿阶段应尽可能选择充足的样本.因而采用2003年1月至2016年8月及2018年10月至2020年10月的Mascon结果作为样本，利用SSA+ARMA方法对2016年9月至2018年9月的结果进行补偿.如图11所示，各流域的TWSA间断补偿结果均取得了较好的效果，补偿结果与CSR RL06 Mascon结果连接较为紧密，且无论是趋势项还是周期特征均与原始时序符合得较好.对于典型流域，利用SSA+ARMA方法可以对GRACE/GRACE-FO空窗期的TWSA间断进行有效补偿.表7为SSA+ARMA与SSA方法补偿结果的统计信息对比.由标准差和均方根值可知，SSA+ARMA方法的补偿结果整体略优于SSA方法，相较SSA方法，SSA+ARMA方法可以顾及到SSA方法未能充分重构的剩余有效信息.

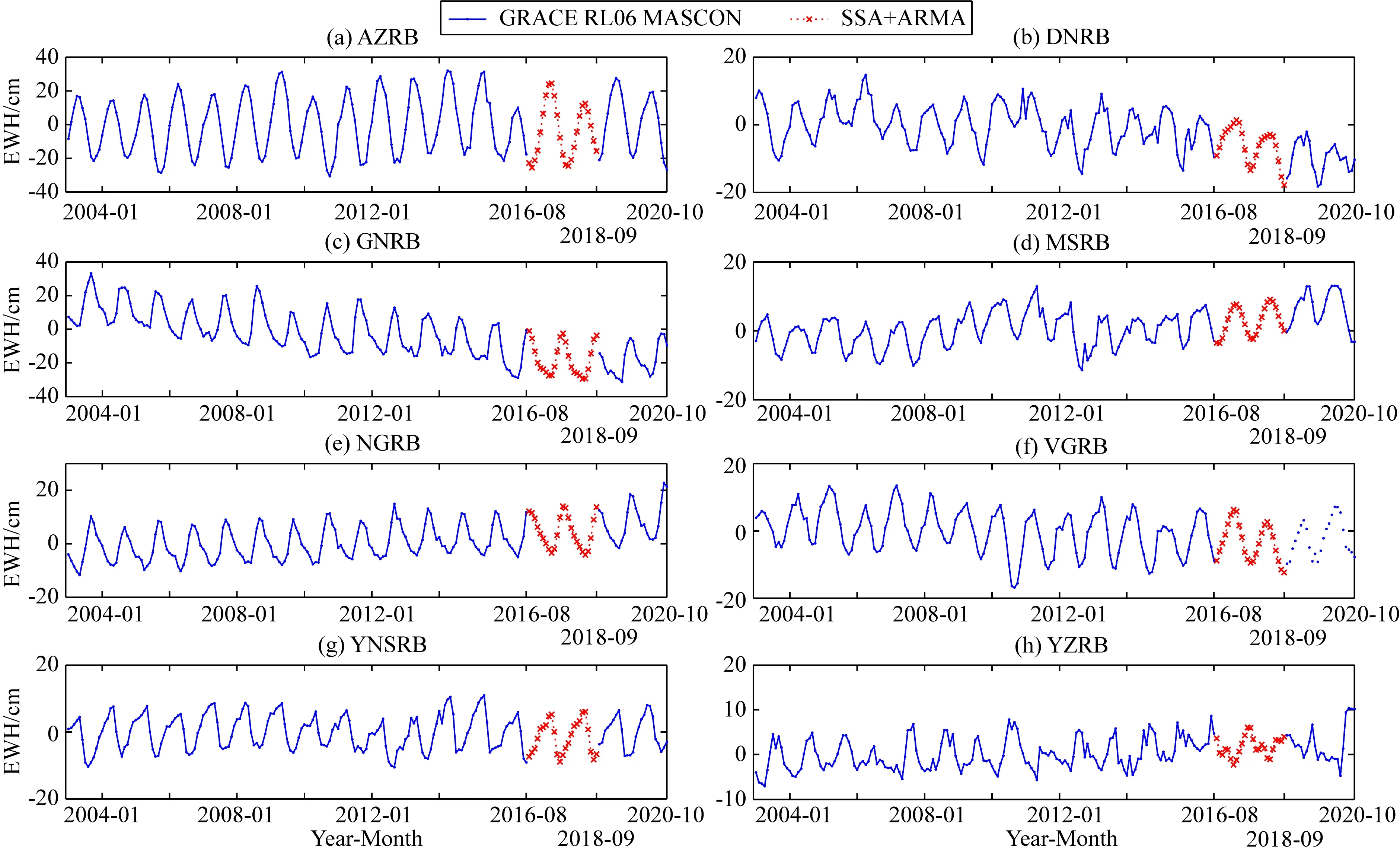
图11 基于SSA+ARMA方法的TWSA间断补偿结果Fig.11 TWSA gap compensation results by SSA+ARMA

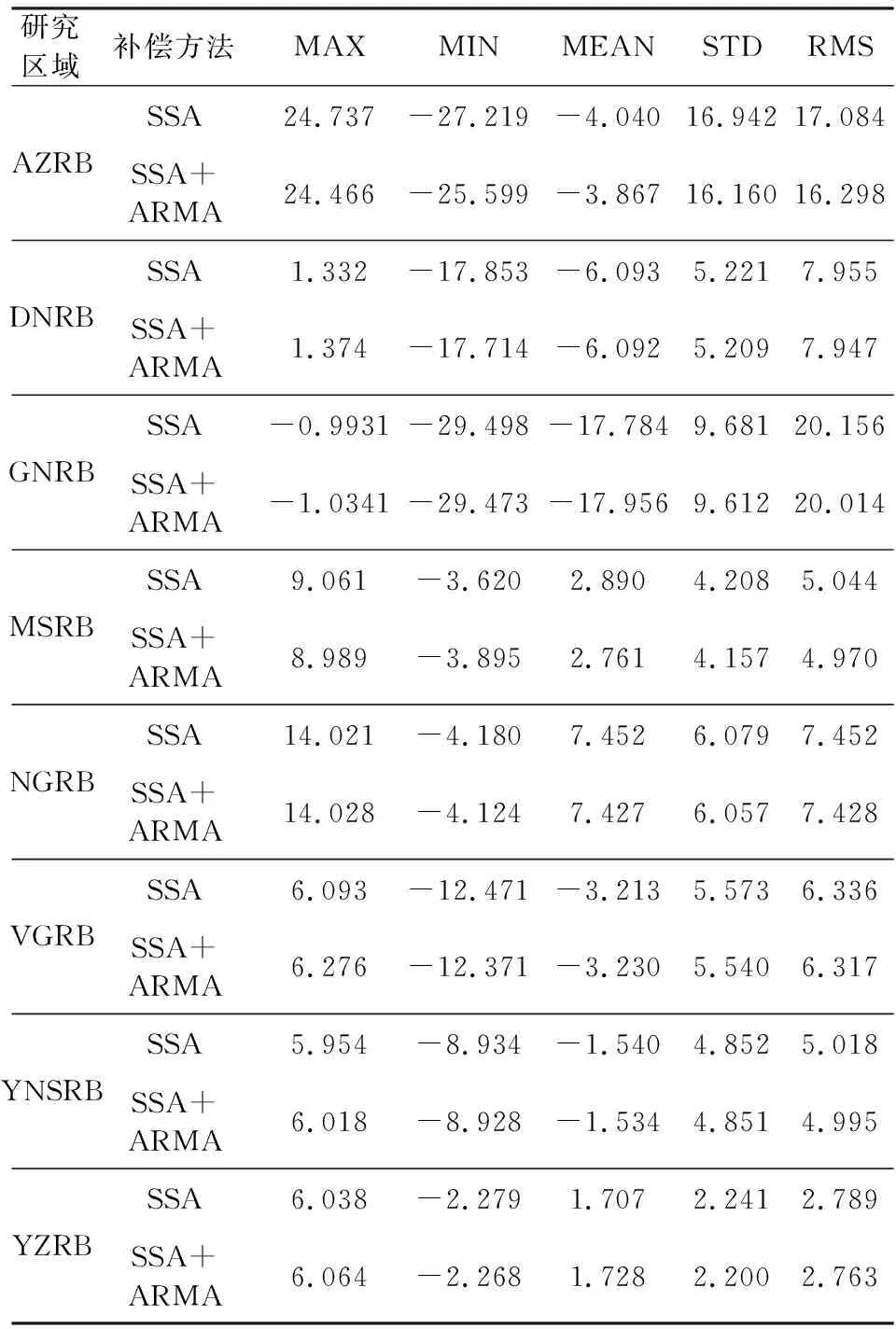
表7 基于SSA+ARMA和SSA的TWSA间断补偿结果统计信息(单位：cm)Table 7 The statistics of TWSA gap compensation results by SSA+ARMA and SSA (Unit: cm)

4 讨论

4.1 SSA预测模型参数确定

FFT及W-correlation方法均为提高构建预测模型效率的辅助方法，本文最终的模型参数确定以预测序列与检验样本的符合精度最高作为准则(包括WNN、ARMA方法).各典型流域均有明显的周年信号，但半年信号在不同流域存在差异，在构建各流域的SSA预测模型时，重构阶数K是否考虑半年信号还应以预测序列与检验样本的符合精度最高为准则.因而本文提出了三种方案来讨论如何选取训练样本、检验样本，构建更适用于间断补偿的SSA预测模型.引入GRACE-FO SH反演TWSA、Mascons结果作为检验样本，不仅能使训练样本更加充足，还能对间断补偿结果进行约束，防止间断补偿结果失真.方案一构建的预测模型A与方案二和方案三构建的预测模型相比表明，充足的训练样本有助于构建更适用于间断补偿的SSA预测模型.方案二的预测模型B的补偿结果与GRACE-FO SH反演的TWSA符合得更好，但可能会导致补偿结果前部分失真(如表5中DNRB、GNRB).方案三的预测模型C对补偿结果的首尾两端均进行约束，但在3.5节中，由于GRACE SH反演的TWSA与Mascons符合精度存在差异的问题，部分流域引入Mascons结果作为检验样本反而可能会导致得不到最佳的预测模型(如表5中MSRB、YNSRB).而3.6节中，当训练样本及检验样本均采用Mascon结果或同种数据时，采用方案三构建预测模型的思路能取得更好的间断补偿效果.方案三的主要思想为引入检验样本对间断补偿结果的首尾两端进行约束，从而构建更适用的预测模型.在实际应用中，训练样本与检验样本的长度可以根据研究目的及需求的不同进行调节.

4.2 SSA与SSA+ARMA方法

SSA+ARMA方法的间断补偿结果整体优于SSA方法，且主要体现在RMSE上，其精度有0.01至1 cm量级的提升.表6可得，SSA+ARMA方法对AZRB、DNRB、VGRB、YZRB的精度提升相对明显，特别是AZRB，基于GRACE-FO SH结果的精度评定中，该流域的RMSE降低了1.01 cm，基于Mascons结果的精度评定中，RMSE降低了1.35 cm.表4可知，AZRB的SSA预测模型C重构阶数K为4，扣除SSA重构序列后的剩余随机时间序列还保留了更多的有效信息，因而再利用ARMA进行外推可以有效提升最终的间断补偿结果的精度.在DNRB、VGRB、YZRB中，预测模型的重构阶数K同样较小.相反，NGRB的预测模型的K为12，因为该流域的TWSA信号周期特征最为显著，SSA方法能充分分解与重构TWSA时间序列，剩余随机时间序列包含的有效信号较少，所以SSA+ARMA方法的补偿结果精度没有明显的提升.当SSA方法无法充分的重构TWSA信号，即预测模型的重构阶数K较小，剩余信号中保留更多的有效信息时，SSA+ARMA方法能更明显的提升间断补偿结果的精度.如表7所示，由最大值、最小值及均值可知，SSA与SSA+ARMA补偿结果的振幅差异较小，大部分差异在0.1 cm的量级.由标准差和均方根值可知， SSA+ARMA方法的补偿结果整体略优于SSA方法，精度提升量级在0.01至0.1 cm，其中在AZRB的精度提升最为明显，标准差降低了0.78 cm，均方根值降低了0.79 cm.相较SSA方法，SSA+ARMA方法可以顾及到SSA方法未能充分重构的剩余有效信息.在以后的实际应用中，对于周期特征弱的非典型流域地区的TWSA序列进行间断补偿时，与SSA方法相比，SSA+ARMA方法可能会取得更好的补偿精度提升效果.

5 结论

本文引入了SSA+ARMA方法对GRACE/GRACE-FO空窗期的TWSA间断结果补偿的方法.联合GRACE SH、GRACE-FO SH、Mascons、GLDAS数据，在AZRB、DNRB、GNRB、MSRB、NGRB、VGRB、YNSRB、YZRB八个流域进行了不同方法的预测试验及SSA+ARMA方法的TWSA间断补偿试验，分别验证了SSA+ARMA方法的适用性及有效性.结论如下：

(1)传统利用多年或前后两年球谐系数均值替代缺失数据的方法会引入较大的误差，而本文采用SSA迭代插值方法的插值结果更符合TWSA序列周期变化的特征，更利于后续SSA方法的周期分解与重构.本文GRACE SH反演的TWSA与CSR、JPL、GFZ的Mascons结果有较好的一致性，大多数流域的RMSE在2 cm以内，NSE、R在0.95以上，验证了反演结果的准确性及可靠性.CSR的Mascons RL05、Mascons RL06结果与GRACE SH反演TWSA结果吻合程度最高.

(2)通过四种方法的预测对比试验发现，在多数流域中，随预测时间长度的增加，四种方法的预测精度逐渐下降，但SSA与SSA+ARMA方法受其影响较小.SSA与SSA+ARMA方法的预测精度较高且相对稳定，相较而言ARMA模型的精度最差.ARMA方法对于周期特征较弱的序列预测效果并不理想(如DNRB、MSRB、YZRB)，而SSA与SSA+ARMA方法取得了较好的效果，这充分体现SSA方法能识别、提取复杂成分信号中有用信息的特性.

(3)SSA+ARMA方法的补偿精度主要受SSA方法补偿精度的影响.引入GRACE-FO SH反演TWSA或Mascons结果作为检验样本，采用更充足的训练样本，可以构建更适用于间断补偿的SSA预测模型，进而能有效提高最终TWSA间断补偿结果的精度.在实际应用中，若引入同种数据作为检验样本，对间断补偿结果的首尾两端进行约束，构建的预测模型能取得更好的间断补偿效果.

(4)基于SSA+ARMA方法的TWSA间断补偿结果有较高的精度，与GRACE-FO SH结果有很强的一致性.除AZRB的RMSE为4.96 cm外，其他流域的RMSE均在4 cm以内；除YZRB的NSE、R分别为0.61、0.80外，其他流域的NSE值均在0.80以上，R值均在0.90以上.

(5)在实际应用的试验中，SSA+ARMA方法的间断补偿结果优于SSA方法，且主要体现在标准差和均方根值上，其精度提升可达0.1 cm量级.相较SSA方法，SSA+ARMA方法可以顾及到SSA方法未能充分重构的剩余有效信息.

综上，本文提出基于SSA+ARMA方法的TWSA间断补偿是可行且有效的，对实现TWSA的长期持续监测有重要的参考价值和科学意义.

致谢感谢匿名审稿专家对本文提出的宝贵意见.