高铁地震面波相速度频散曲线提取

温景充， 石永祥， 宁杰远,2*

1 北京大学地球与空间科学学院, 北京 100871 2 河北红山地球物理国家野外科学观测研究站， 河北邢台 054000

0 引言

中国东部人口众多，经济发达.为促进经济发展和提高人民生活水平，迫切需要进行诸如地下空间利用、智慧城市建设、高铁地基病害自动监测、资源和能源勘探、地震预测等方面的工作，地震学探测和监测不可或缺.但是，中国东部地震震源的缺乏严重制约了该区域地下结构的探测与监测.

高铁运行所产生的桥梁和路基振动是一种全新的优质绿色震源，能够激发出稳定的、重复性强的地震波场，应用前景很好.以利用高铁振动信号为目的的大规模学术研究始于2018年.三年来，中国科学家在高铁震源信号特征、高精度建模、高铁地震波场理论、高铁震源反演、近地表成像及反演等方面取得了突破性研究进展，初步证实了运行中的高铁列车所激发的振动是研究地球浅部介质结构、物性及其变化的优质人工震源(王晓凯等，2019a，b；刘磊和蒋一然，2019；张固澜等，2019；曹健和陈景波，2019；蒋一然等，2019a，b；鲍铁钊等，2019；温景充等，2019a，b；温景充和宁杰远，2019；Wang et al.，2021；Chen and Cao，2020；Liu et al.，2021).

国外科学家近年来利用重载列车进行了类似研究.其中，Brenguier等(2019)利用台阵策略和背景噪声方法，提取出跨断层传播的重载铁路体波信息，进行了与断层结构变化相关的研究，显示重载列车的信号在50 km以外仍然能被观测到.除体波外，由于铁路震源靠近地表，会产生振幅较大的面波，特别是近地表存在低速松散沉积物的情况下表现得更为明显(Takemiya，2008).因此，有必要尝试是否能够从铁路地震信号中提取出面波信息.

面波相速度成像是获取浅层波速结构的有效手段.传统的基阶面波频散曲线提取方法包括单台法、双台法(Sato，1995)、双平面波法(Forsyth et al.，1998)等.其中单台法获取的是震源与台站间的平均频散曲线，而双台法要求震源与两个台站近似在同一大圆弧路径上，得出两台站间的平均频散曲线.背景噪声面波方法是通过两个台记录的互相关获取经验格林函数(Campillo and Paul，2003)，要求噪声源分布均匀且相干性较低.但是，高铁作为移动组合源，既不符合天然地震的特点，也不满足背景噪声方法的要求，因而需要新的处理方法.

同时，研究者曾经提出了利用单个六分量地震仪提取单点处频散曲线的方法(Igel et al.，2005；Kurrle et al.，2010)，本文称其为旋转法.旋转地震仪记录的高铁地震信号如何用来研究地下结构是值得探讨的问题.

张唤兰等(2019)基于垂直于高速铁路的测线，利用反卷积方法，恢复经验格林函数，从中明显可见体波和面波成分，但未进一步从中提取面波相速度.Quiros等(2016)在重载铁路附近布设平行于铁路的测线，对体波和面波进行了尝试性提取，并尝试利用基阶和高阶面波频散曲线进行S波速度结构反演，但未考虑铁路震源的复杂性.因此，如果希望把面波方法扩展到研究高铁线路两侧的波速结构，有必要对传统的面波频散曲线提取方法是否适用于高铁地震信号进行研究.

本文通过计算分层介质的理论频散曲线，模拟出面波格林函数，进一步与高铁震源时间函数进行卷积，得到模拟的高铁地震面波记录.将传统面波方法应用于模拟记录时发现，并不能够直接获取正确的频散曲线.基于理论分析，结合高铁地震波场干涉特征，本文提出了针对高铁地震信号提取面波频散曲线的新方法.

1 高铁地震信号的面波提取方法

1.1 双台法

双台法最早是应用在天然地震中.若震源与两个台站近似位于一个大圆弧路径上，则面波近似沿两台站的连线传播.为了测量面波在这两个台站间传播的相速度，需要获取相位信息.通常，通过对两个台站的地震记录进行互相关测量相速度.由于时域互相关对应于频域上一个台站的记录乘另一个台站记录的复共轭，因此互相关记录的相位即为所需测量的相位差.从互相关记录中提取出相位差φ(ω)，进一步能够计算出相速度c(ω)=ωΔ/φ(ω)，其中Δ为两台站的台间距.由于我们更关注高铁作为移动组合源所产生的特殊地震波对面波方法的影响，因此先不关注面波方法中去噪、频散曲线挑选等细节，而只强调方法的基本原理.

1.2 旋转法

随着旋转地震仪相关技术的不断进步，近年来利用单台六分量地震记录获取单点处频散曲线的相关方法开始进入研究人员的视线.该方法的优点是不需要对两个台的记录进行互相关，仅需要单台就能够获取频散曲线.从原理上看，这一方法应该对震源的分布没有特殊要求，因为不同方位角传过来的波具有轴向对称性，是等效的.但必须明确其方位角，从而获取切向分量的加速度.

综上，六分量地震仪所记录到的水平切向加速度和绕竖直轴旋转的角速度成正比，该比值与波的相速度有关.分别对两者进行窄带滤波，计算其幅值之比，则能够计算该频率面波的相速度，获取面波频散曲线.目前，该方法主要应用于勒夫波，而在瑞利波上的应用较少.

1.3 面波方法在高铁数据中的应用

双台法和旋转法均要求入射波近似为平面波，而高铁震源为复杂的移动组合源，所激发的波场显然不满足两方法的基本要求.因此，需要通过分析高铁波场的特征，对两个方法进行一定的调整.考虑到我国东部平原地区大部分高铁线路架设在高架桥上的现状，本文仅讨论以桥墩为固定分立震源所激发高铁地震远场波场的特征及面波方法在其中的应用.

把等间距的桥墩视为点源，所得到的高铁地震远场波场会表现出一定的干涉特征(温景充等，2019b).具体表现为，某一特定频率的波会有一个或多个优势的干涉叠加方向，这些方向可由一个简单模型计算出来.如图1所示，若频率为f的波在与垂直于高铁的法线夹角为θ的方向上传播，相邻两桥墩所激发的波能够叠加增强，则应满足两列波的到时差为周期T=1/f的整数倍，即：

图1 干涉叠加增强示意图Fig.1 Schematic diagram showing superposition enhancement of an interference field

(1)

其中L为桥墩间距，v为高铁运行速度，c0(f)为面波相速度，k为正整数.

如果给定相速度频散曲线c0(f)，对于每一个干涉级数k，都能够在一定的频率范围内算出一个角度θ与之对应.若取本文计算中使用的速度模型对应的勒夫波相速度(如图3所示)，取桥墩间距为32 m，列车速度为64 m·s-1时，计算结果如图2所示(国内高铁桥墩间距的典型值为32 m，高铁和动车速度分别约为80 m·s-1和64 m·s-1，车厢长度典型值约为25 m，本文选取这些典型值进行计算).

图2 不同频率的波叠加增强的方向 图中红色、绿色、蓝色、青色和粉色分别对应式(2) 中k为1到5的情况(图5—8同).Fig.2 The directions in which waves of different frequencies are superimposed and enhanced The red, green, blue, cyan and pink colors in the figure correspond to the cases where k is 1 to 5 in equation (2) (same in Figs.5—8).

图中显示，干涉级数越高，覆盖的频率范围就越宽.在某些特定的频段，没有可叠加增强的方向；而一些较高的频率可能有不止一个优势方向.本文将有且仅有一个优势叠加方向的频率范围称作有效频率范围.

在远场条件下，认为某一频率的面波近似为沿优势叠加方向传播的平面波，则若将双台垂直于高铁线路放置，则这一平面波的传播方向与双台连线方向的夹角即为θ，双台法的理论测量值为视速度c2(f)=c0(f)/cosθ(下标“2”表示 “双台”).联立该式和式(1)可以得到，在有效频率范围内，双台法测量结果和模型相速度之间应满足关系：

(2)

在给定模型相速度的时候，可以根据式(2)对有效频率范围内的双台法测量结果进行预测；而若已有双台法测量结果，则可利用该式对测量结果进行校正.

使用单台旋转法时，需要先知道勒夫波的传播方向，以得到相应的切向加速度.在平面波的假设下，若所选取的切向与实际的切向存在夹角θ，则相应的用于计算的切向加速度为实际的切向加速度在这个方向上的投影，而旋转地震仪所测得的绕竖直轴旋转的角速度没有变，因此单台旋转法实测值c1=c0cosθ(下标“1”表示 “单台”).与双台法分析过程相似，将该式与式(1)联立，可以给出旋转法的方程：

(3)

同样地，可以利用式(3)对有效频率范围内的旋转法测量结果进行预测或校正.

以上两种校正方法都需要已知桥墩间距L以及高铁行驶的速度v，这两个量并不难测得，但车速的测定可能会有一定的误差(王晓凯等，2019b).若需要进一步应用到实际中，则可能会面临桥墩间距不等、列车加速减速以及波速横向不均匀的情况.因此，还可以考虑一种不需要已知桥墩间距和车速的方法.

考虑到双台法所测得的相速度会比实际偏大，实测值c2=c0/cosθ；单台旋转法实测值会比实际偏小，实测值c1=c0cosθ，可以将两个测量值取几何平均值进行校正.由于双台法所得到的是两台站之间的平均相速度值，而旋转法得到的是单一台站附近的相速度值，因此这一校正应要求速度结构横向差异较小，或者双台间距不大，且用于测旋转分量的单台位于双台之间.

2 数值实验

对本文高铁地震面波相速度频散曲线提取方法有效性的理论测试，需要首先进行关于已知介质结构或已知频散曲线下的面波波场正演模拟，然后再对正演的理论数据进行面波相速度提取，观测是否能恢复已知频散曲线.

2.1 高铁远场地震面波模拟

2.1.1 高铁桥墩震源

关于高铁地震的正演模拟，前人已有相关工作.Chen和Cao(2020)给出了高铁震源格林函数的理论表达式.温景充等(2019b)也将高铁桥墩视为点源，通过计算一定介质下的格林函数，叠加不同桥墩对台站的格林函数卷积震源时间函数的结果，获取远场模拟波场.其中，所谓远场，是要求观测点到桥墩的距离远大于桥墩的尺度和桥墩间距，即观测点与高铁线路的距离至少在百米的量级.本文的理论测试沿用这种正演思路，将桥墩视为等间距的点源.震源位置确定后，进一步需要计算每个震源的时间函数.

2.1.2 震源时间函数

传统格林函数对应的源是单力点源，因此需要得到高铁行驶经过时，单个桥墩的作用力随时间的变化，作为震源时间函数.Wu和Yang(2004)将桥梁视为弹性梁，而假设桥墩为刚性，并设桥梁与两侧桥墩之间由一个等效弹簧连接.通过求解梁的振动，得到单个桥墩在列车驶过时作用在刚性桥墩上的力，作为震源时间函数.作为近似，可以将桥梁也视为刚性，且认为桥梁与桥墩间刚性连接，仅考虑车轮以点力的形式作用在桥梁这一刚体上时，桥梁对两侧桥墩的力(温景充等，2019b).这一假设下所计算出来的结果与将桥梁视为弹性梁的模拟结果在中低频上是非常相似的.因此，在理论测试中使用这一简单方法给出单桥墩的震源时间函数，相关参数为8节车厢，每节车厢长度为25 m.将l方向的震源时间函数在频域中记为Sl(f).

若列车匀速行驶，高铁线路近似为直线，且桥墩均匀分布，则不同桥墩的震源时间函数之间仅存在一个与列车到时相关的时间延迟.可以将列车车头到达第n个桥墩的时刻记为τn，则τn=nτ，其中τ=L/v，即桥墩间距比列车速度.这一时间延迟可以在频域表示为e-i2πfτn.

2.1.3 面波格林函数

考虑到高铁地震信号的主要频率在2 Hz以上，对应于百米量级的浅部，因此选择近地表简单的三层平层模型作为生成模拟数据的理论模型.在高铁线路密集的我国东部平原区域，这一深度范围一般是S波速度较小(Takemiya，2008；吕国军等，2017)且泊松比较大的松散沉积.本文在此基础上确定计算中的波速和密度.其中三层P波速度分别为800、1000和1200 m·s-1，密度分别为2600、3000和3300 kg·m-3.相应的S波速度结构以及通过理论计算得到的瑞利波、勒夫波频散曲线分别如图3a、b所示.

图3 三层S波波速模型(a)及理论频散曲线(b)Fig.3 Three-layer S-wave velocity model (a) and theoretical dispersion curves (b)

由于旋转法主要应用于勒夫波，因此主要考虑位移的水平分量.基于三分量的震源时间函数，计算三分量位移，同时利用间距很相近的几个台的水平位移，计算位移梯度，从而给出旋转的竖直分量的理论结果.

2.1.4 模拟信号结果

利用上述方法，可以获得不同位置处台站的模拟面波记录.距离高铁1.0 km的台站处的三分量位移记录如图4a所示；平行于高铁水平分量加速度和绕竖直轴旋转的角速度分别如图4b、c所示.

图4 合成记录 (a) 三分量位移； (b) 平行高铁水平分量加速度； (c) 绕竖直轴的旋转角速度.Fig.4 Synthetic records (a) Three-component displacement; (b) Horizontal acceleration parallel to high-speed rail; (c) Angular velocity of rotation around the vertical axis.

2.2 面波相速度提取结果

2.2.1 预测结果与实测结果

利用(2)式，可根据给定的相速度模型，预测双台法瑞利波和勒夫波相速度测量结果；而利用(3)式，则可预测旋转法勒夫波相速度测量结果.如预测结果与实际测量结果比较接近，则相当于证实了可用(2)、(3)式进行相速度校正.在展示预测值时，仅展示有效频率范围的结果.

取桥墩间距为典型值32 m，车速分别为80 m·s-1和64 m·s-1，双台与高铁线路的距离分别为1.0 km和1.1 km，且双台连线与高铁线路垂直的情况，所得到的预测值与合成数据的相速度测量结果如图5所示.对于两种车速的情况，双台法瑞利波和勒夫波的预测值与实测值都基本吻合.旋转法结果显示，在每一段有效频率范围内，在中心频率左侧二者比较吻合；而在中心频率的右侧，预测值与实测结果明显拟合不上，在车速为64 m·s-1时表现为实测值偏小，而在车速为80 m·s-1时表现为实测值偏大.在某些频段，比如车速为64 m·s-1时的4 Hz附近，以及车速为80 m·s-1时的2.5 Hz附近，出现了较大偏差.

图5 相速度预测值与实测结果 (a)、(b)、(d)、(e)为双台法结果； (c)、(f)为旋转法结果.图中红色虚线为模型值，灰色粗实线为预测值，黑色虚线为实测值(图6同).Fig.5 Predicted phase velocities and the measured results (a), (b), (d) and (e) show the results of two-station method; (c) and (f) show the results of rotational method. The red dashed lines show the model values, the gray thick solid lines represent the predicted values, and the black dashed lines are the measured values (same in Fig.6).

总地来说，无论是瑞利波还是勒夫波，双台法结果的预测值和实测值是大体吻合的.而对于旋转法，误差较大.旋转法的误差可能来源有两个.其一是旋转法本身的误差(Igel et al.，2005)；另外是对于高铁这一组合移动源，勒夫波会和瑞利波的水平分量叠加，从而影响横向加速度，而瑞利波的水平分量不会引起绕垂向的旋转，因此用旋转法所测结果会受瑞利波干扰.为了验证这一推测，考虑在模拟数据中增大勒夫波的振幅，将勒夫波的振幅分别增大到原来的2倍和5倍，所得结果如图6所示.明显可见随着勒夫波振幅增大，旋转法的测量结果与预测值之差明显减小.

图6 不同勒夫波振幅的相速度预测值与实测结果 (a)、(d) 1倍振幅； (b)、(e) 2倍振幅；(c)、(f) 5倍振幅.Fig.6 Predicted phase velocity and the measured results with different Love wave amplitudes (a) and (d) Original amplitude; (b) and (e) Double amplitude; (c) and (f) Quintuple amplitude.

2.2.2 校正结果

上文所述实测结果与预测结果的对比，说明双台法结果可以通过公式(2)进行校正且效果较好；而旋转法结果用(3)式校正后可能仍有较大误差.下面同时给出有效频率范围内瑞利波双台法、勒夫波双台法、勒夫波旋转法以及勒夫波联合校正的结果，如图7所示.无论是瑞利波还是勒夫波，双台法基本能够恢复有效频段范围的频散曲线，旋转法的校正结果在每段有效频率中左侧的结果优于右侧，而联合校正结果略优于旋转法，但不如双台法.

对于本文所用参数对应的相速度值，10 Hz以下，车速为80 m·s-1(图7a)对应的有效频率范围分别在2.2～3.0 Hz、4.2～6.2 Hz、6.4～8.2 Hz以及9.7～10.0 Hz之间；而车速为64 m·s-1(图7e)对应的有效频率范围分别在1.8～2.2 Hz、3.5～4.7 Hz、5.2～6.8 Hz、7.2～8.5 Hz以及9.8～10.0 Hz之间.叠加二者的结果能够得到更多频率点处的相速度值，从而可以用于反演更精细的S波速度结构.

图7 不同校正方法得到的相速度 (a)、(b)、(e)、(f)为双台法结果，(c)、(g)为旋转法结果，(d)、(h)为联合校正结果；蓝色虚线为双台法测量结果， 蓝色实线为旋转法测量结果，黑色实线为校正结果(图8同).Fig.7 Phase velocity obtained by different correction methods (a), (b),(e), and (f) show the results of two-station method, (c) and (g) show the results of rotational method, (d) and (h) show the results of joint correction. The blue dashed lines show the measurements of two-station method, the blue solid lines show the measurements of rotational method, and the black solid lines show the correction results (same in Fig.8).

受高铁列车空间周期性的影响，高铁信号的频谱表现出等间距分立谱的特征(王晓凯等，2019a)，使得信号中某些频率的能量被压制.如果数据中存在较大的噪声，则可能会对这些能量较低的频段的相速度值产生影响.为了了解噪声对面波方法的影响程度，在模拟数据中分别加入不同幅度的随机噪声，所得双台法勒夫波相速度结果如图8所示.结果表明当信噪比大于20时，噪声对双台法相速度的影响较小，而随着信噪比降低，相速度测量的误差不断增大，特别是在7 Hz以上的频段.

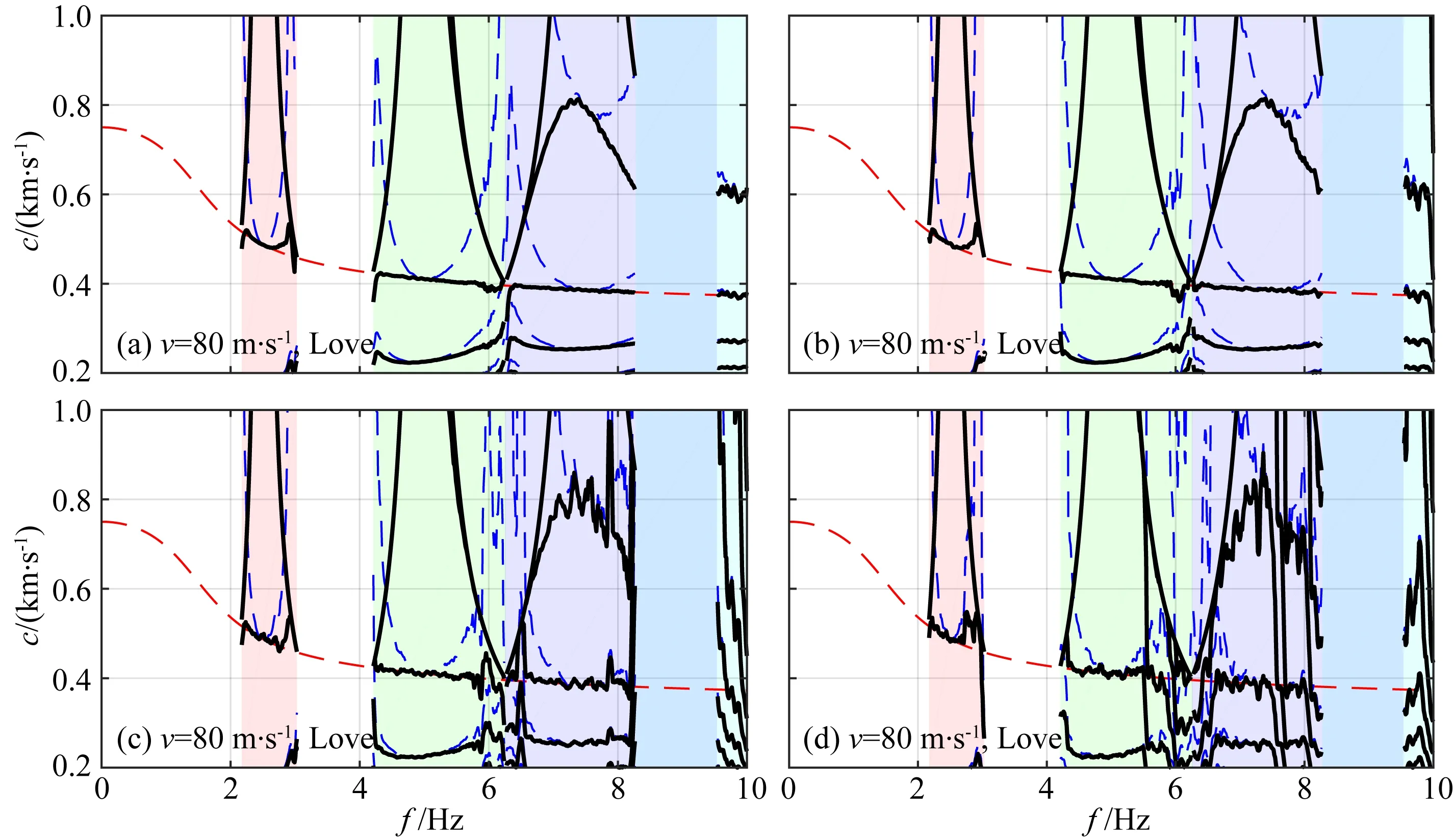
图8 含噪声模拟数据提取的相速度 信噪比分别为(a) 50； (b) 20； (c) 5； (d) 2.Fig.8 Phase velocity obtained from synthetic records with noises The signal-to-noise ratios are (a) 50; (b) 20; (c) 5; (d) 2.

3 讨论

3.1 不同校正方法的使用

若使用双台法获取瑞利波的相速度频散曲线，则需要通过公式(2)对结果进行校正.但是瑞利波相速度和S波、P波波速相关，如果浅层介质为松散沉积层，其波速比较大，不利于用瑞利波相速度反演S波速度.勒夫波速度仅与S波速度结构相关，因此可以考虑提取勒夫波频散曲线.提取勒夫波频散曲线也可以使用双台法，其校正后误差较小，但是具有多值的特点，可以结合旋转法所得单个相速度值进行频散曲线的进一步拾取.对于横向不均匀的情况，各频率的面波主要传播方向无法通过理论预测，则考虑使用双台法与单台法联合校正.该校正方法或可拓展应用于其他复杂组合源激发的面波频散曲线提取.

3.2 应用于实际数据时可能的挑战

接下来，我们计划采集需要的野外观测数据.将高铁面波提取方法应用到实际数据中，可能会遇到噪声、仪器响应不准确等方面的挑战.

噪声是绝大多数实际数据处理过程中都会遇到的问题.对于高铁地震记录而言，由于高铁列车的空间周期性，使得高铁地震记录的频谱往往呈现等间距分立谱的特征.这意味着在某些特定的频率处能量特别突出，而很多频率范围的能量被压制.若在被压制的频率范围内，噪声的能量高于信号的能量，则有可能造成在这些频率范围内无法正常计算.初步测试结果显示，要得到良好的相速度结果，高铁地震信号的信噪比应大于20.

由于使用旋转法提取面波相速度的过程中需要将切向加速度与绕竖直轴的角速度的幅值相除，因此需要明确知道仪器记录的加速度与真实加速度之间的关系，即准确的仪器响应.旋转地震仪亦是如此.若没有准确的仪器响应，则不能得到准确的相速度频散曲线.若不同频率的仪器响应一致，则在不知道仪器响应的情况下，也能大致得出一个频散曲线，只不过得到的是相对值，而不能获得绝对值.这一相对值可用于监测波速变化.

3.3 高铁面波反演的有效范围

利用面波进行浅部结构反演时，频率越低，能够反演的深度越深.考虑我国高速铁路桥梁、桥墩间距以及车速的实际情况，能够稳定叠加增强的最低频率在2 Hz左右.若近地表存在松散沉积，其S波速度为数百米每秒的量级，则可反演的深度在100 m范围内；若地表无松散沉积，则其S波速可能会大一个数量级，相应可反演的最大深度在1 km左右.

而在横向上，则需要考虑高铁信号的有效传播距离.已有观测数据(温景充等，2019a)显示未经叠加的高铁信号在3.5 km外有明显的波形，但高频(10 Hz以上)的数据在1 km外几乎不可见.本文的计算则表明，Q值取为50时，距离高铁4 km处台站的最大振幅约为距离高铁1 km处台站最大振幅的1/20，高频的衰减则更快一些.再把远场条件和信噪比要求考虑进来，总地来说，距离高铁300 m到3 km的范围内为信号的有效范围.

3.4 其他面波方法的适用性

双台法结果在经过校正后能较好地恢复频散曲线，而该校正要求已知车速和桥墩间距，且假设介质横向近似均匀.若考虑横向不均匀的情况，各频率的面波主要传播方向无法通过理论预测，则考虑使用双台法与单台法联合校正.由于旋转分量的信息可以由台阵位移记录的梯度给出，因此这种联合校正的方法本质上是利用了更多台的信息.而实际上，利用三个台，就可以求解出某一频率面波的传播方向及相速度.因此，基于台阵数据分析的直射线层析成像方法(Barmin et al., 2001)、双平面波法(Forsyth et al., 1998)、Eikonal成像方法(Lin et al., 2009)、Helmholtz方法(Lin and Ritzwoller,2011)或可直接应用于高铁面波相速度层析成像，相关方法的测试结果将在另文讨论.

4 结论

本文进行了高铁地震信号面波相速度提取的理论测试，从理论上预测了不同频率面波的优势叠加方向，将双台法和单台旋转法应用于模拟高铁地震面波数据的相速度频散曲线提取并进行校正，得到以下结论.

(1)以桥墩为震源的高铁地震波场具有一定的干涉特征，对于面波来说，某频率的优势叠加方向可通过给定桥墩间距、列车车速以及面波相速度进行理论计算.

(2)双台法与单台法提取面波频散曲线时，其误差主要来源于面波传播方向与预设方向的偏差.结合对面波干涉场的理论分析，给出了频散曲线测量的预测值，并与模拟数据的频散曲线提取结果进行比较，证明了可以通过本文给出的公式(2)和(3)校正相速度值.

(3)通过对双台法获取的相速度结果进行校正，或者对双台法与旋转法的结果取几何平均值，能够一定程度上恢复有效频率范围的频散曲线.在模拟面波记录中加入噪声，结果显示信噪比大于20的数据能给出相速度结果.综合不同车速的结果，能得到频散曲线，进一步反演近地表最深1 km内，距离高铁300 m到3 km范围的S波速度结构.

致谢研究工作得到了北京大学高性能计算校级公共平台支持．感谢中国科学院地质与地球物理研究所李幼铭研究员及高铁地震学联合研究组对高铁地震观测和研究的大力支持.感谢北京大学盖增喜副教授、张海明副教授、李正斌教授和蒋一然博士研究生提供的有益建议.感谢匿名审稿人及地球物理学报编辑部的辛勤付出及建设性意见.