瞬变电磁扩散场到虚拟波场的精细积分变换算法

鲁凯亮, 李貅*, 戚志鹏*, 樊亚楠, 周建美,李文翰, 李贺, 张明晶, 王扬州

1 长安大学地质工程与测绘学院， 西安 710054 2 长安大学地球物理场多参数综合模拟实验室(中国地球物理学会重点实验室)， 西安 710054 3 山东大学齐鲁交通学院， 济南 250061 4 山东省交通规划设计院， 济南 250031 5 北京探创资源科技有限公司， 北京 100071

0 引言

目前瞬变电磁反演结果为连续电阻率的空间分布，在识别电性分界面等构造时具有一定的困难.而瞬变电磁的拟地震成像是实现三维成像的有效手段之一(Xue et al.，2013；戚志鹏等，2013；钟华森等，2016).在实现拟地震成像之前，需要把瞬变电磁扩散场转换到虚拟波场.只有在此基础上，才能实现稳定高效的瞬变电磁法拟地震解释.

瞬变电磁扩散场主要描述的是低频电磁场传播过程中的扩散和感应特征，具有较强的体积效应，因而对电性界面的分辨能力较差(Khan et al.，2018；底青云等, 2019; Di et al.，2020；Xue et al.，2019；Li et al.，2018)；而波动场能够比较好地描述波场的一系列特征，所以基于波动方程的拟地震成像可以很好地刻画地层的界面信息(Qi et al.，2015).而直接将瞬变电磁的扩散场引入至波场的处理流程中是不合适的，需要通过数学手段进行变换.Lee等(1989)给出了虚拟波场到扩散场的积分公式，实现了稳定的正变换；随后，Lee和Xie(1993)根据波场正变换的积分公式，尝试进行波场反变换的计算，他们指出波场反变换需要求解第一类的Fredholm积分方程，属于严重的不适定性问题.之后，Gershenson(1997)分别使用了直接求解法、反褶积法和拉氏正弦变换法计算虚拟波场，并对这三种方法的优劣进行了比较.陈本池等(1999)使用正则化方法进行虚拟波场反变换的求解，并对层状模型进行试算，结果表明从扩散场转换至虚拟波场后，在电性分界面处会出现“反射”和“折射”等现象，这一发现为电磁场的拟地震处理解释提供了重要的理论依据.近些年，李貅等(2005)，朱宏伟等(2010)，张军等(2011)将正则化算法应用于波场反变换中，取得较好的结果；戚志鹏等(2013)通过使用预条件正则化共轭梯度法，实现了全时域的虚拟波场反变换算法，通过引入地震勘探中的脉冲反褶积方法，提高了虚拟波场的纵向分辨率.樊亚楠等(2019)使用扫时波场变换算法，进一步提高了波场反变换的稳定性.虽然以上方法都取得了长足的发展，但是虚拟波场反变换的精度和效率还有待进一步提高.

在计算虚拟波场反变换时，将其离散化后的线性方程组具有高度的病态性.近年来，精细积分法作为求解高度病态线性方程组的方法，在各个领域得到了日益广泛的应用.该方法通过把求逆矩阵的过程转化为一个求解无穷积分的过程，大大降低了求解病态线性方程组的难度.精细积分法(钟万勰，1994)在计算矩阵指数函数时，具有效率高、精度高等优点，已经在各类工程问题中取得了较大进展(Gu et al.，2001)，而目前将精细积分法引入到虚拟波场反变换的工作鲜有提及，本文将对这一方法的引入初做尝试.

1 波场变换基本原理

1.1 基本原理

在导电介质中，忽略位移电流，瞬变电磁场满足扩散方程.为了不失一般性，取f(x,y,z,t)为瞬变电磁场的电磁分量.

根据文献(Lee et al.，1989)可知，瞬变电磁扩散场转换到虚拟波场的表达式为

(1)

式(1)为第一类Fredholm型积分方程，从扩散场求解虚拟波场是一个典型的不适定问题.对式(1)进行离散，可以得到：

(2)

其中：

(3)

离散后得到的线性方程组是高度病态的，且随着阶数的增加，矩阵的条件数急剧增大(戚志鹏等，2013)，本文采用精细积分法求解(1)式.

图1 核函数曲线图Fig.1 Kernel function graph

1.2 精细积分法

考虑病态线性方程组

Ax=b,

(4)

式中A为n阶正定矩阵，b为n维实向量，记H=-A、r=b，则式(4)可以转化为

Hx+r=0,

(5)

考虑如下一阶微分方程

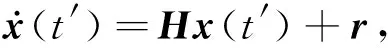
(6)

式(6)是瞬态热传导方程解的形式；稳态的热传导方程的解具有式(5)的形式，而式(6)的解可以表示为

上式中，H是负定矩阵，r为常向量.从上式易知，当时间t′→∞时，方程(6)趋向于方程(5)，且容易看出exp(Ht′)→0，所以式(7)中的积分项就逼近式(5)的解，即

(9)

所以，式(4)的解就可以写为(富明慧，2018)

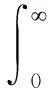
(10)

从上面的分析我们可以得出一个结论，病态线性方程组的求解可以转化为一个求积分的稳定过程.

(11)

1.3 迭代终止准则

前文主要介绍了精细积分法，这一节给出迭代终止条件.理论上讲，迭代次数越多，结果越精确，但是当积分区间达到一定数值范围后，随着计算误差的累积以及矩阵的高病态性，反而会导致精度随积分区间的增加迅速下降，所以有必要在虚拟波场计算的过程中添加一个迭代终止条件.

目前有如下四种迭代终止条件：(1)对迭代次数设置一个迭代上限m；(2)终止条件设置为errk<ε，ε为给定的误差容限，errk=‖xk+1-xk‖；(3)当迭代残差有单调下降和单调上升的两个计算过程时，理想的迭代终点在残差的拐点处，即当errk/errk-1≥1时迭代终止；(4)在第k次计算过程中，往后逐次取n个迭代步，如果这n个迭代步的相对残差都在增长，默认第k次的解为最优解.

对于第一种终止条件，更多的是以经验为主，要么没有达到精度要求，要么增加不必要的计算量；第二种终止条件在应用于病态方程组时经常失效(富明慧和李勇息，2018)；第三种终止条件太过理想，在实际计算中的残差曲线往往并非单调，而且经常有波动.综上，本文选取第四种终止条件.

设

(12)

式中n为选择的检测窗口，为整数，一般情况下取2，最大不超过10(富明慧和李勇息，2018).

2 高斯脉冲的波场反变换

2.1 算法精度

首先研究一个简单脉冲，令u(τ)=1

从图2的结果可以看出，对于简单脉冲u(τ)=1，本文的方法与正则化共轭梯度法都能得到相对较好的结果，但是相较而言，本文结果的精度比较高.

图2 波场反变换结果和相对误差 (a) 本文方法结果； (b) 本文方法相对误差； (c) PRCG结果； (d) PRCG相对误差.Fig.2 Inverse wave field transformation results and relative error (a) The present method; (b) The relative error in paper； (c) The PRCG method; (d) The relative error by PRCG.

接下来本文使用单个高斯脉冲和组合高斯脉冲的方式来得到更加复杂的虚拟波场.令u(τ)为高斯脉冲，它的表达式如下：

(13)

式中，a表示高斯脉冲的峰值大小，c表示高斯脉冲的宽度，τ0表示高斯脉冲的峰值位置，h0表示高斯脉冲在垂直方向的偏移量.通过给定不同的a、c、τ0和h0的值就可以得到不同样式的高斯脉冲，而且还可以对上式进行组合得到更加复杂的高斯脉冲序列.

使用精细积分法分别计算了D型、G型、Q型、A型、H型和K型模型的虚拟波场(图3)，并与前人研究结果进行了精度对比.从相对误差图上可以看出，本文方法的相对误差较小，均在4%以下，而正则化共轭梯度法的相对误差随着模型的复杂而逐渐增大，最大相对误差达到了将近50%，从这里可以看出本文方法具有较高的精度.

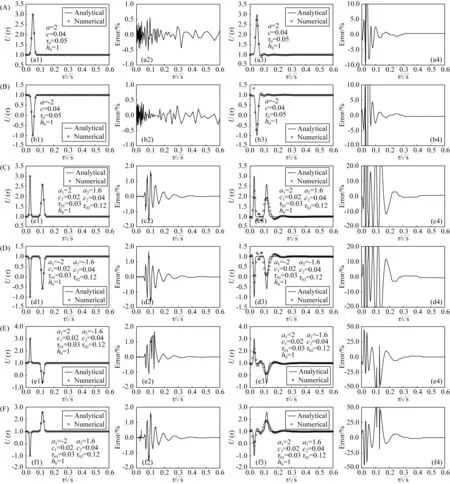
图3 不同型模型波场反变换结果和相对误差 (A) D型模型； (B) G型模型； (C) Q型模型; (D) A型模型; (E) H型模型; (F) K型模型.(a1—f1) 本文方法结果； (a2—f2) 本文方法相对误差； (a3—f3) PRCG结果；(a4—f4) PRCG相对误差.Fig.3 The inverse transformation results and relative errors of thedifferent model (A) D model; (B) Gmodel; (C) Q model; (D) A model; (E) H model; (F) K model; (a1—f1) The present method; (a2—f2) The relative error in paper; (a3—f3) The PRCG method; (a4—f4) The relative error by PRCG.

2.2 模型分辨率分析

令第一个脉冲的脉宽为0.02，振幅为2；第二个脉冲的脉宽为0.04，振幅为1.6；使第一个脉冲的波峰位置为τ01=0.03，改变第二个波峰τ02的位置，使其分别为0.04和0.08.结果如图4所示：

本节研究了本文方法对Q型、A型、H型和K型模型的分辨能力(图4).固定第一个脉冲的波峰位置为τ01=0.03，改变第二个波峰τ02的位置，使其分别为0.08和0.04，使得两个波峰的位置越来越近.从上述结果可以看出，本文方法具有较好的分辨能力，而随着两个波峰的位置越来越近，正则化共轭梯度法的分辨能力越来越低.

图4 波场反变换结果 (A) Q型模型； (B) A型模型; (C) H型模型; (D) K型模型; (a1—d1) 本文方法结果τ02=0.08；(a2—d2)PRCG结果τ02=0.08； (a3—d3) 本文方法结果τ02=0.04； (a4—d4) PRCG结果τ02=0.04.Fig.9 The inverse transformation results and relative errors of the different model (A) Q model； (B) A moel; (C) H model; (D) K model; (a1—d1) The present method τ02=0.08; (a2—d2) The PRCG method τ02=0.08; (a3—d3) The present method τ02=0.04; (a4—d4) The PRCG method τ02=0.04.

2.3 加噪试验

分别对D型、G型、Q型、A型、H型和K型模型的扩散场中分别加入2%和5%的噪声，并计算对应的虚拟波场.计算结果如图5.

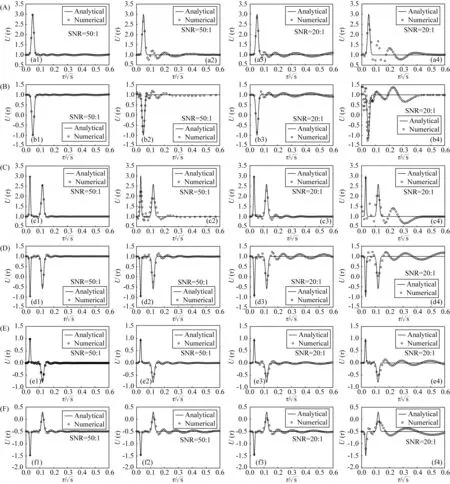
图5 不同模型加噪波场反变换结果 (A) D型模型; (B) G型模型; (C) Q型模型; (D) A型模型; (E) H型模型; (F) K型模型; (a1—f1) 本文方法结果SNR=50∶1； (a2—f2) PRCG结果SNR=50∶1； (a3—f3) 本文方法结果SNR=20∶1； (a4—f4) PRCG结果SNR=20∶1.Fig.5 The inverse transformation results and relative errors of the different model (A) D model; (B) G model; (C) Q model; (D) A model; (E) H model; (F) K model; (a1—f1) The present method SNR=50∶1; (a2—f2) The PRCG method SNR=50∶1; (a3—f3) The present method SNR=20∶1; (a4—f4) The PRCG method SNR=20∶1.

图5各模型的扩散场信号中加入2%和5%的噪声，测试了本文方法和正则化共轭梯度法的抗噪性.从图中可以看出，本文的方法抗噪能力比较强，对于含有2%和5%噪声的扩散场，依旧能求取较为准确的虚拟波场；对于含有2%噪声的扩散场，PRCG可以较为准确地求取对应的虚拟波场，对于含有5%噪声的扩散场，求得的虚拟波场结果较差.当信噪比超过5%时，两种方法的虚拟波场结果波动剧烈，与真值差距较大.因此对于野外信号的采集必须控制噪声在5%以下，并且对于局部不光滑数据不能直接求解，需要对数据进行平滑降噪后才能计算虚拟波场.

3 三维模型计算

为了进一步验证本文使用的波场反变换算法的有效性，本节设计如下三维模型计算虚拟波场，并与正则化共轭梯度法进行比较.图6为均匀半空间中含有两个低阻薄板状异常体的模型示意图.均匀半空间的电阻率为200 Ωm，上层异常体上表面距离地表150 m，几何尺寸为100 m×100 m×20 m，电阻率为5 Ωm；下层异常体上表面距地表250 m，几何尺寸为100 m×100 m×30 m，电阻率为1 Ωm.接地导线源的长度为200 m，最短偏移距为100 m，发射电流为10A；布设13条测线，测线的线距为10 m，起始测线位置为y=-80 m，终止测线位置为y=50 m，每条测线长度为500 m，点距为25 m，每条测线21个测点，接收的电磁场信号为Ex.本文三维正演采用拟态有限体积法(Zhou et al.，2018).

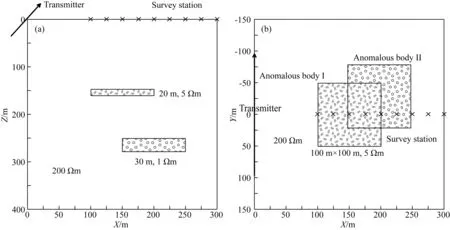
图6 三维模型示意图 (a) XOZ平面图； (b) XOY平面图.Fig.6 Schematic diagram of three-dimensional model (a) XOZ plan; (b) XOY plan.

图7为波场反变换结果，本文在这里只展现三条测线的波场反变换结果，分别是测线y=-70 m，测线y=0 m，测线y=30 m.选取这三条测线的原因是测线y=-70 m能反映出深部异常信息；测线y=0 m可以反映浅部和深部的异常信息；而测线y=50 m可以反映出浅部异常信息，其他测线的结果与这三条测线的结果类似，所以在此不进行展示.

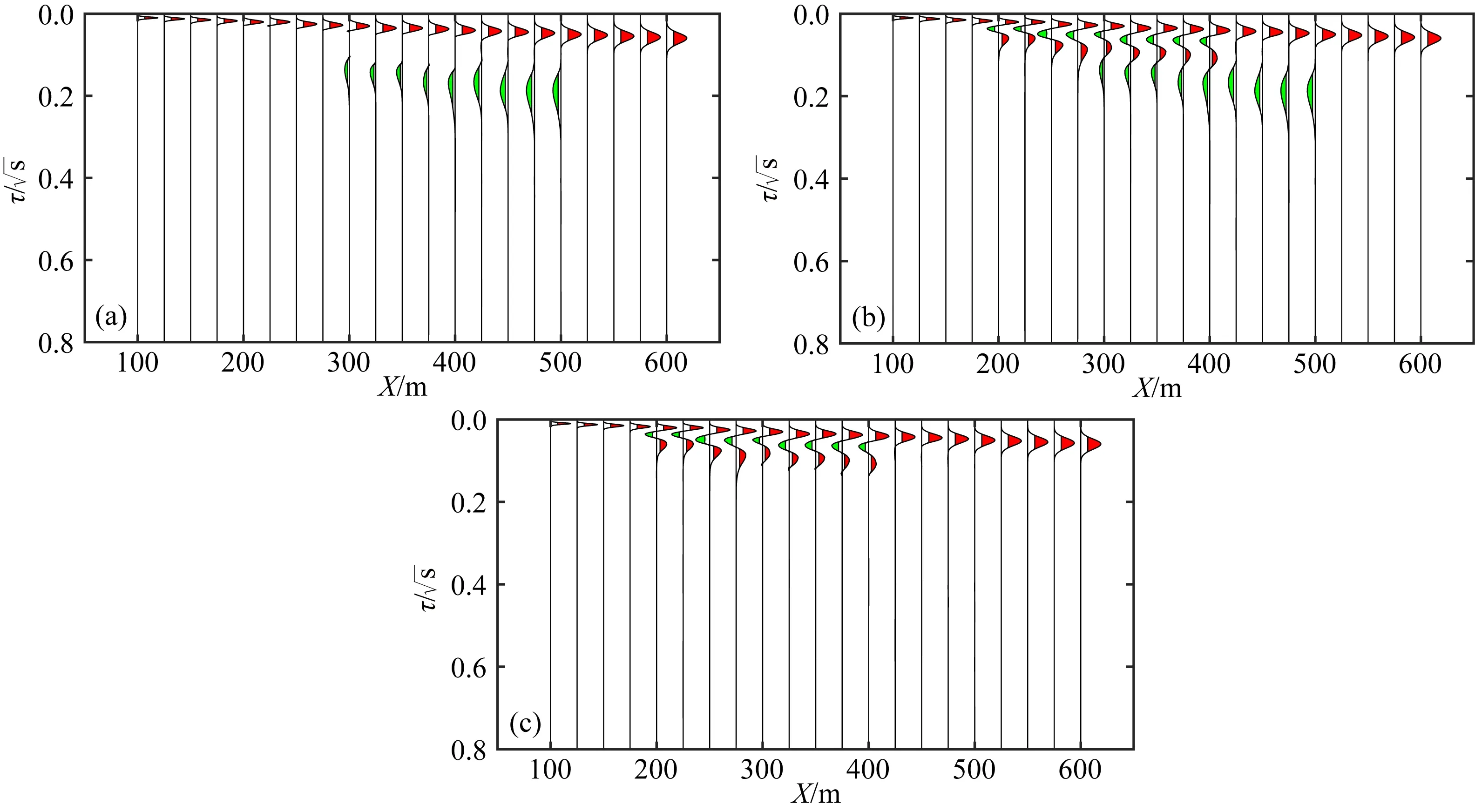
图7 本文方法波场反变换结果 (a) 测线y=-70 m； (b) 测线y=0 m； (c) 测线y=30 m.Fig.7 Results of wave field transformation in this paper (a) Line y=-70 m; (b) Line y=0 m; (c) Line y=30 m.

图7a是测线y=-70 m的波场反变换结果，从图中可以看出，除了直达波以外，还有深部异常体的上界面信息，由于瞬变电磁的高频成分被地层迅速吸收，所以导致对深部异常体的分辨率较差；图7b是测线y=0 m的波场反变换结果，从图中可以看出，虚拟波场可以很好地反映出浅部异常体的上下界面，波形的同相轴比较明显；对于深部异常体，图7b也能反映异常体的上界面信息；图7c是测线y=50 m的波场反变换结果，能够反映出浅部异常体的界面信息.从三幅图中可以看出，使用本文方法计算的结果，虚拟波场比较平滑，在整个时间段，无意义的波动起伏也比较少.

图8为使用PRCG方法得到的波场反变换结果.可以看出，只有测线y=-70 m的结果比较好；测线y=0 m的结果主要反映的是深部异常体上界面的部分信息；测线y=50 m对浅层异常体界面反映较好，但是由于PRCG方法的精度较低，出现了多余的虚拟波场.

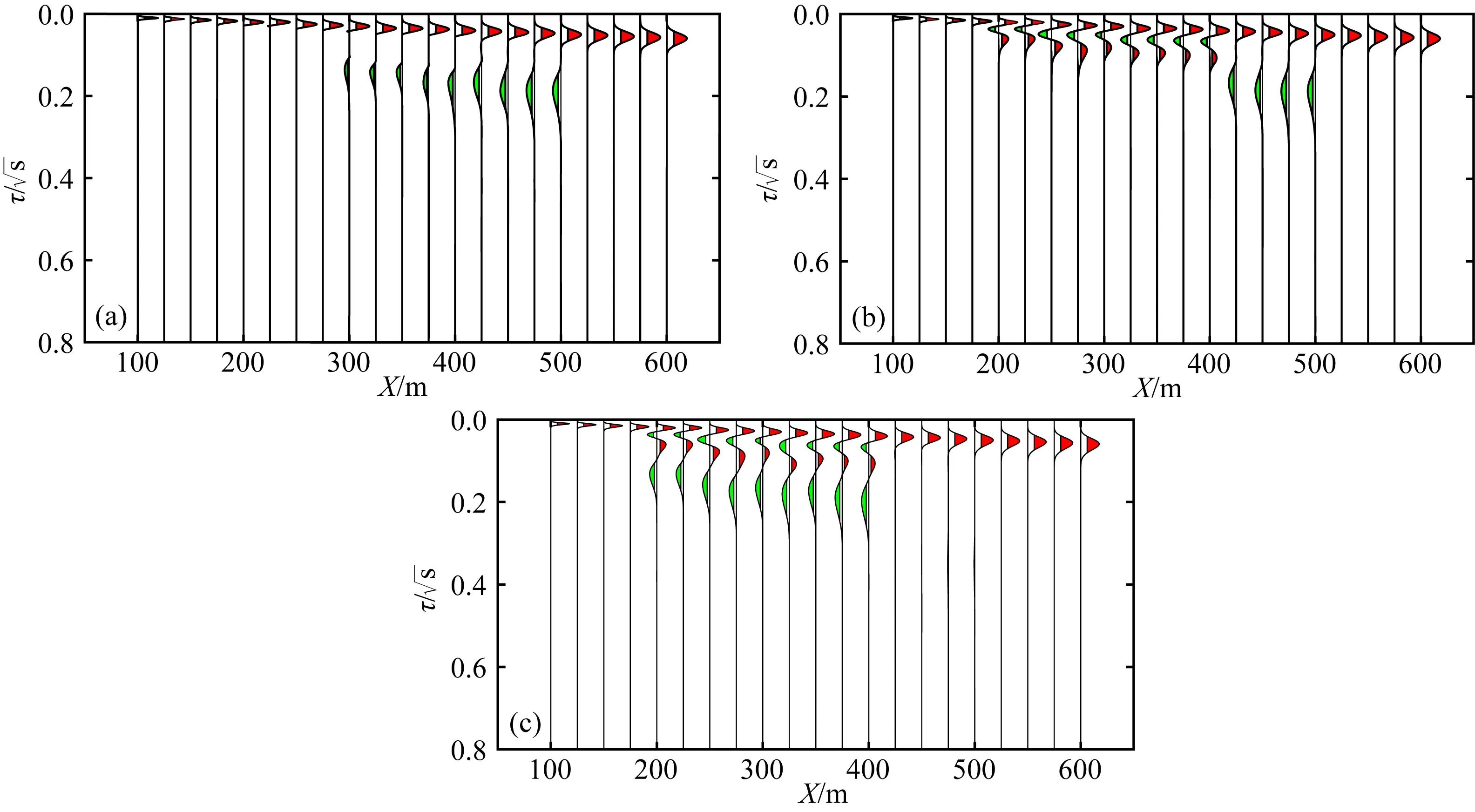
图8 PRCG波场反变换结果 (a) 测线y=-70 m； (b) 测线y=0 m； (c) 测线y=30 m.Fig.8 Results of wave field transformation by PRCG (a) Line y=-70 m; (b) Line y=0 m; (c) Line y=30 m.

图9是本文方法的虚拟波场三维切片图，共有四张切片，对应的位置分别为y=-50 m，y=40 m，x=120 m和x=240 m.从图中可以看出，位置(1)和位置(2)处可以很清楚地反映异常体在xoy平面的位置，位置(3)和位置(4)处也能较好地反映出深部异常体在xoy平面的位置.通过计算，三维模型的虚拟波场与设计模型相符，可以进一步说明本文方法的有效性和准确性.

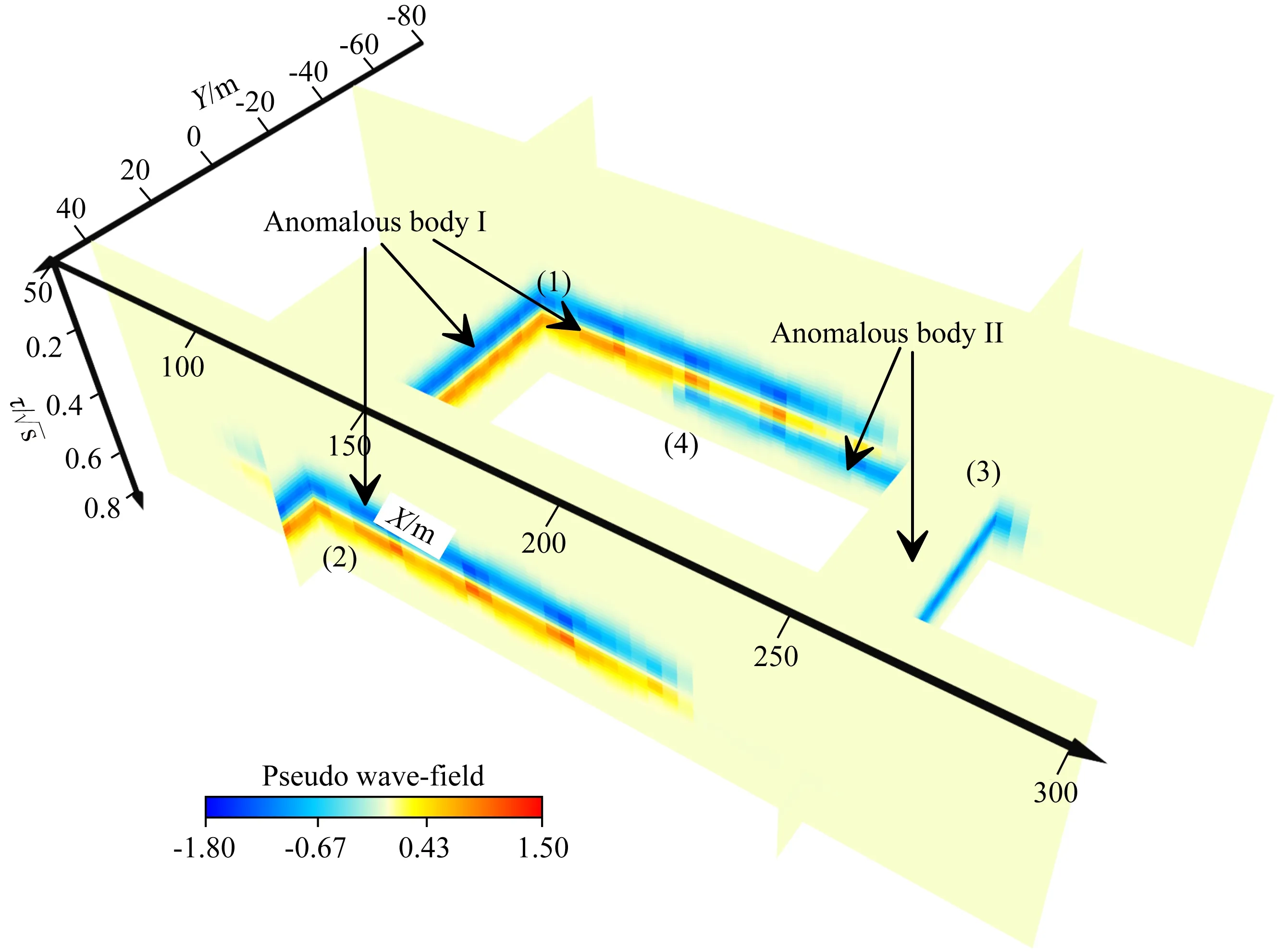
图9 波场反变换结果三维切片图Fig.9 Three-dimensional slice map of wavefield transformation results

4 实测数据分析

上文利用各种算例与模型对本文方法进行了验证，本节对甘肃省某煤田采空区实测数据进行处理.采区地层大部分被第四系黄土覆盖，基本隐蔽,部分基岩裸露.地层从上到下由上白垩统、下白垩统、上侏罗统、中下侏罗统及上三叠统组成，中下侏罗统为主要煤系地层，上三叠统为煤系基底.采区主要含煤地层由石英细粗砂岩、砂砾岩、炭质泥岩、炭质粉砂岩组成.采区地表南部为丘陵，部分丘陵的白垩纪岩层出露.地表北部开阔平缓，为农田及低矮丘陵，小冲沟发育.地表中部、北部有两条季节性沙河.

野外工作使用V8多功能电法仪器，发射系统采用地面长导线源，发射电流15 A，基频8.3 Hz，共15条测线；每条测线400 m，点距10 m，共41个测点，沿南北向布设，接收Ex电磁信号.本文选取380号测线数据进行视电阻率成像(张莹莹等，2015)与波场反变换，其余测线不在此文赘述.

由图10a视电阻率剖面图可以看出，随着深度的增加，视电阻率值总体呈现先减小后增大的趋势.在测线的280～320 m、340～400 m、440～500 m处，高程在800～1000 m之间，有三个低阻异常区，推断可能为煤矿采空区塌陷，导致裂隙发育形成富水区域，从而形成低阻异常区，与已知的钻孔资料较为吻合(已知钻孔的煤线高程为1042.93 m).由图10b可以看出，虚拟波场的同相轴与视电阻率的趋势基本一致，整体呈南低北高，与煤层底板等值线图较吻合(图11).在测线的280～320 m、340～380 m、400～430 m，430～500 m处，由于煤层被开采，地层错断较为严重，在虚拟波场图上表现出横向不连续，间断跳跃的特征.本文通过与已知资料对比，本文的计算结果与已知资料相吻合，说明本文方法在识别电性界面方面有较好的效果.

图10 380号测线视电阻率图(a) 与波场反变换结果(b)Fig.10 Apparent resistivity profile and pseudo wave field of line 380

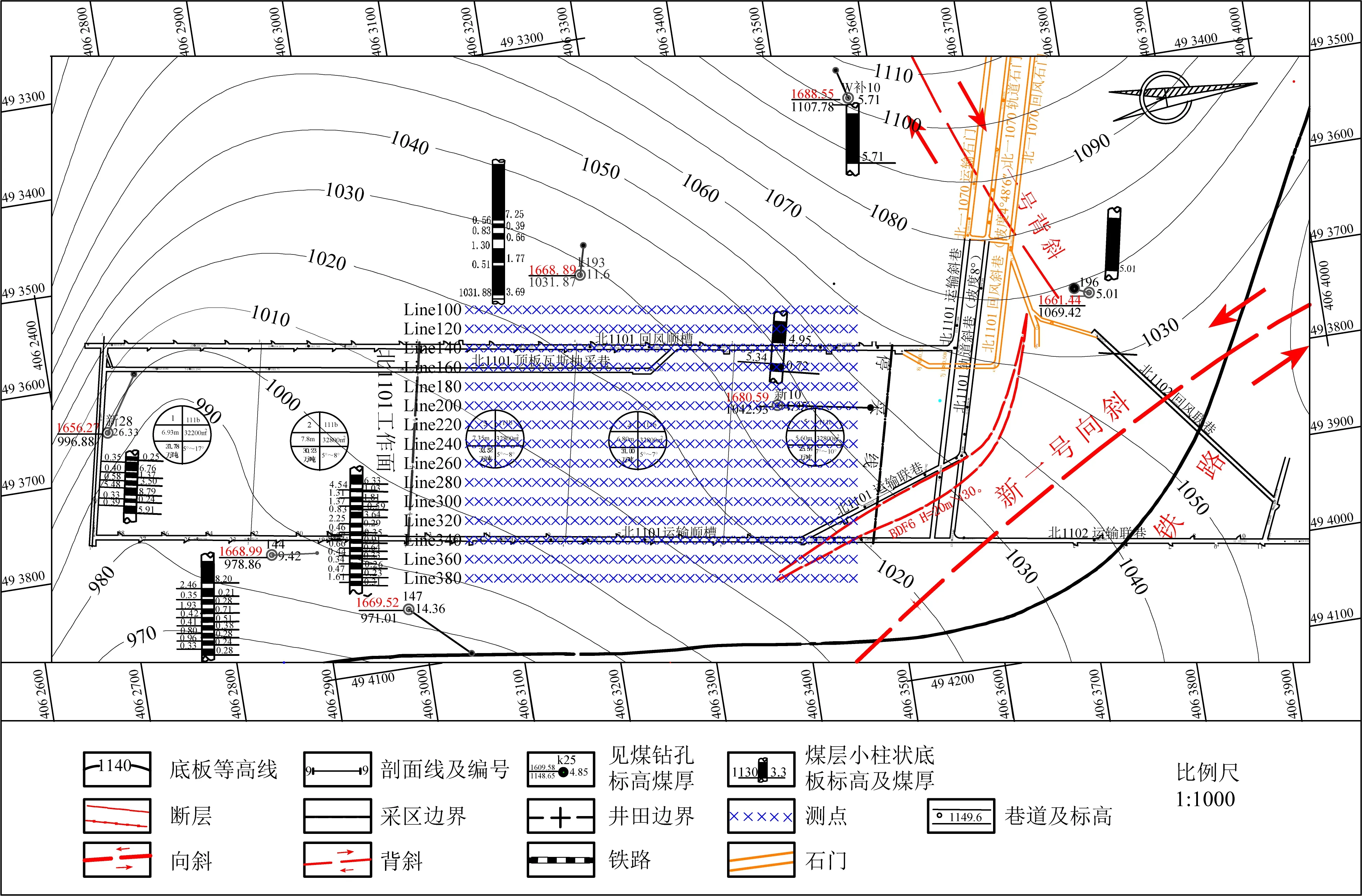
图11 工区煤层底板等值线图Fig.11 Contour map of coal seam floor in working area

5 结论

本文通过使用精细积分法，成功实现了从瞬变电磁扩散场到虚拟波场全时域稳定的反变换算法.在保证计算精度的前提下，使用指数级的积分步长可以显著提高计算效率.通过设置合理的终止迭代条件，使得本文的方法适用性更广.

实现波场反变换后，本文对算法进行了验证.通过对典型地电模型的计算，证明了本文的方法具有较好的精度(得到虚拟波场值与理论值的误差小于4%)、分辨能力以及抗噪性，可以说明本文方法适用于复杂介质模型.通过计算三维模型的虚拟波场值，可以看出虚拟波场对浅层异常体的分辨率较好，随着深度增加，高频成分很快被吸收，低频成分占主导，波场幅值减小，子波宽度增加，分辨率逐渐降低.最后通过对实测数据的处理，进一步说明了本文方法的可行性，为后续的瞬变电磁构造成像方法打下了良好的基础.

从文中可以看出，当扩散场包含的噪声越来越大时，波场反变换的结果与实际结果相差也就越大.因此，在后续工作中可以引入窗口扫描、相关叠加的方法进一步提高该方法的抗噪性.

致谢感谢中山大学富明慧教授在作者研究过程中给予指导，同时感谢论文评审专家和编辑提出的宝贵修改意见

附录A

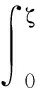
(A1)

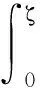
(A2)

类似地，我们可以得到：

(A3)

此时对两边同时乘以b，得：

(A4)

当k→∞时，我们将得到精确解xk.但是精细积分的步长ζ一般都比较小(富明慧和李勇息，2018)，如果对积分区间[0,∞)采用线性等间隔离散，计算量将大到无法接受.所以本文参考前人工作(钟万勰，1994)，采用指数增长的积分步长.

对于矩阵指数函数，钟万勰提出了一种精确且高效的计算方法，在各类偏微分方程中获得了广泛应用.与上文类似，设

(A5)

对上式两边同时乘以b，得：

x1=(I+exp(-Aζ))x0.

(A6)

由于ζ是极小量，在计算矩阵指数函数时，可使用Taylor展开的前几项：

(A7)

对式(A7)在区间[0,ζ]积分，得

(A8)

综上，x的初始值x0=F(ζ)b.

令积分步长以2k-1ζ变化，则有

k=1,2,…

(A9)

且当2kζ→Fk时，有

(A10)

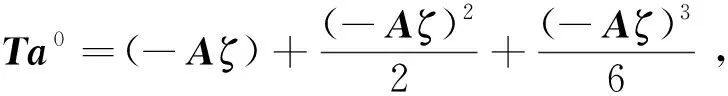
(A11)

上式中Tk即为矩阵指数函数的值，这样计算矩阵指数函数的好处在于：在计算过程中当k很小时，能将大量和小量分离，避免小量与大量相加时出现数据“湮没”，保证计算精度(富明慧和李勇息，2018).