流行病在城市空间中的传播模拟*——以新型冠状病毒(COVID-19)疫情期间的武汉市主城区为例

叶锺楠

1 研究背景

1.1 疫情下规划思考

2019 年12 月，新型冠状病毒疫情(COVID-19)在中国武汉市暴发，并在短短3个月内席卷了上百个国家（图1），引起全球高度重视的同时，也引发了社会各界对于流行病传播预测的又一轮关注和思考。对于城市规划领域而言，需要关注的不仅仅是疫情持续的时间和感染人数，更需要关注疾病传播和城市空间的关系：包括被感染人群在城市中的空间分布特点、不同的城市空间格局对流行病传播趋势的影响等。

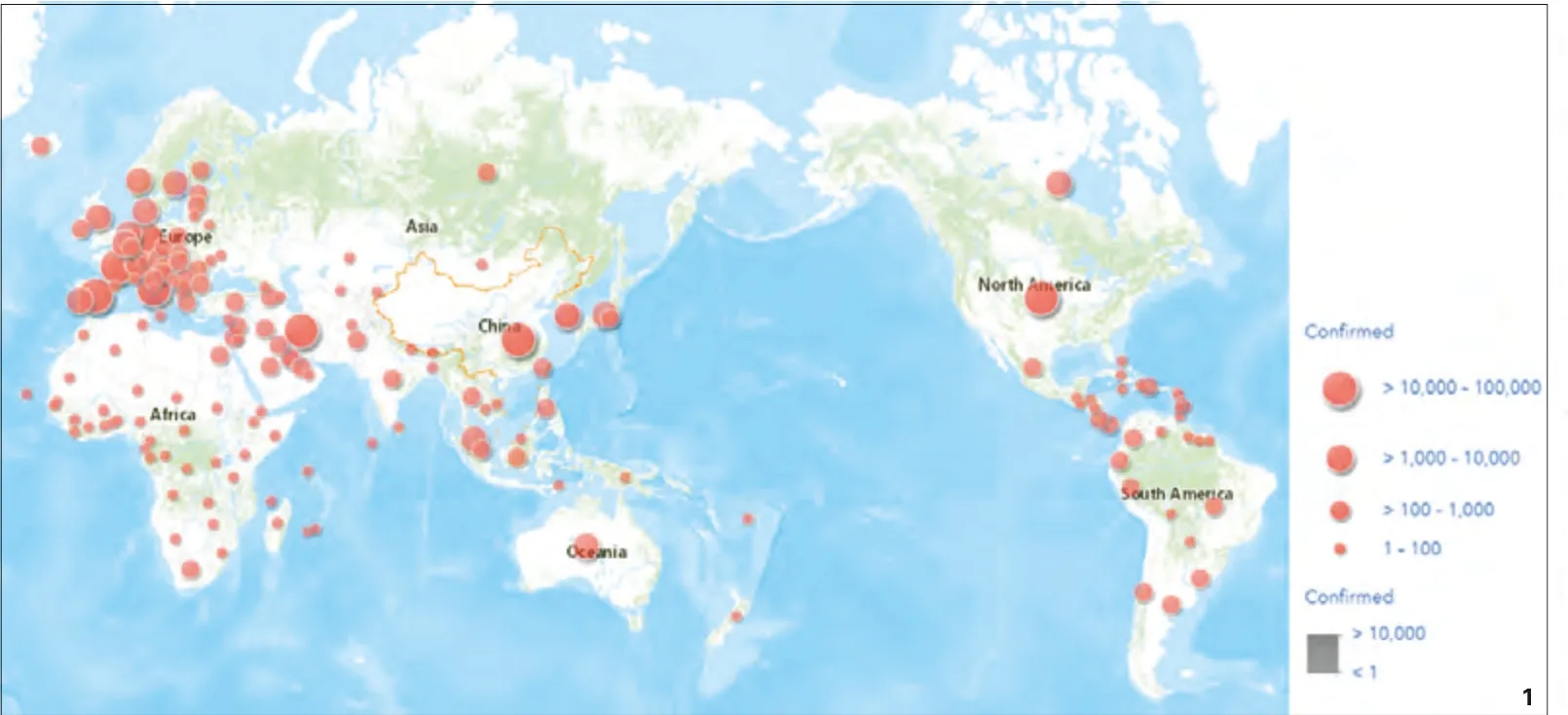
图1 全球COVID-19 病例分布（2020 年3 月20 日）

为此，本研究尝试以武汉中心城区为对象，结合城市的空间结构，构建以社群单元为节点的复杂网络，并通过基于智能体的建模来对流行病在社群单元之间的传播进行模拟，进而推演整个城市范围内的疫情发展情况。考虑到整个疾病传播的过程中，政府主导的各种防控措施对疫情的实际走向产生了重要影响，在本文所建立的模型中，还对各种公共卫生干预措施的效果进行了模拟，以使模型的运行尽可能接近真实情况。

1.2 流行病传播模型研究综述

从流行病传播模型的发展历程来看，最初主导的领域是医学和数学，早在1760 年瑞士数学家Daniel Bernoulli就提出了天花接种策略的数学模型[1]，20 世纪以来，随着模型对复杂度、精确度要求的提高和科学技术的发展，流行病的研究方法也逐渐从传统的勘察统计和简单数学模型扩展到复杂网络分析和计算机模拟，计算机、系统控制和复杂科学等学科在流行病传播模型的发展中所起的作用越来越显著[2]，相比之下，尽管城市一直是流行病传播的“重灾区”，但城市规划领域对流行病传播模拟和预测的研究却相对较少[3，4]。

从模型考虑和关注的要素来看，无论是早期的数学模型还是目前应用最广泛的系统动力学仓室模型（如经典SIS、SIR、SEIR 模型等），都是从人群和疾病特征出发，预测疫情持续的时间和感染的人数，对于疾病传播过程中空间要素的影响和传播结果的空间属性关注相对较少，现有的将空间要素纳入考虑的研究中又以理想网络和区域体系下的传播研究为主，对基于真实网络和对城市内部的研究较少。

此外，现有的流行病传播空间模型在表达人群行为对疫情的反馈方面具有普遍的局限性，事实上从本次COVID-19 疫情在中国的发展可以看到，无论是人们在知晓疫情后自发的防护行为（戴口罩、注重卫生）还是政府主导的公共卫生干预（隔离防治、病患排查等），都能够对疾病的传播产生重大影响，因此，将人的行为纳入疾病传播的过程进行动态计算是流行病传播模型的发展趋势[5]。

2 基于智能体的城市流行病传播社群单元模型构建思路

基于智能体的建模方法（Agent-Based Modeling，ABM）是分布式人工智能的一种，其运作方式是建立一系列有自主分析和决策能力的智能体（agent），并通过这些智能体的行为和互动来模拟真实世界的运行[6]。ABM 在模拟复杂系统方面具有独特的优势，在社会研究、宏观经济、系统控制、军事和城市研究等领域都有着广泛的应用。

流行病在城市中传播的过程是一个由传播要素（疾病）、大量自主性主体（人）和它们的交互行为综合作用下的结果，具有典型的复杂系统的特征，传统的观察和研究方法很难对其运行规律进行量化和总结，而基于智能体的模型则能够通过对主体及其交互活动的分布式模拟来实现对疫情整体传播和扩散情况的描述和预测。

本研究尝试以Netlogo 为模拟平台1），结合ABM 方法和城市空间的结构特征，将经典流行病预测模型中的传播机制融入以城市社群单元和长短程连接为基础的空间网络中，以实现流行病在城市空间中的传播情况以及公共卫生干预效果的模拟（图2）。

图2 模型构建思路图示

2.1 节点：社群单元

从对象单元来看，传染病传播模型的构建思路可以分为单一群体方法、微观个体方法和复合群体方法。单一群体方法将具有共同特征的人群视为一个整体，考察不同特征人群之间的交互，最常见的有以SIR 模型为代表的各种仓室模型；微观个体方法以单个个体为模拟对象，在最大程度上体现个体的异质性；复合群体方法介于上述两者之间，通过建立一系列的社群单元来代表在地理或社会关系等方面具有同质性的各类群体，社群单元之间的交互通过网络实现[6]。

单一群体方法一般难以体现空间特征，而微观个体方法多用于小尺度研究，其表达的细节在城市整体尺度意义不大，因此本研究主要采用复合群体方法，根据地理相近原则建立社群单元，一个社群单元可以代表街坊、社区、楼宇或家庭。每个社群单元即为网络的一个节点，通过社群单元的数量和分布来表达城市的密度和空间结构。在城市总体尺度观察和分析模型时，把每个社群单元视为一个点，其内部的互动和疾病传播情况简化为一组动力学方程或者一个概率常数。

2.2 网络：短程连接和长程连接

传播动力学研究通常以复杂网络为基础，常见的复杂网络包括随机网络（random network）、无标度网络（scale-free network）、小世界网络（small-world network）等，一般认为人类社交网络具有无标度网络的特征，而地理空间更接近小世界网络的结构[7-9]。

为此，研究以小世界网络为基础，通过建立短程和长程两种连接实现节点之间的交互，短程连接在节点周围一定距离随机建立，用来模拟城市个体在社区影响范围内（如15min 生活圈等）的日常活动；长程连接则在外围节点和中心节点之间建立，用以模拟城市个体的工作通勤以及较为大型的消费休闲活动，为了使模型更符合城市空间结构特点，在建立长程连接时增加了偏好依附法则，以增大其连接到城市中心或邻近副中心的概率。

2.3 传播机制：基于SEIR 分类的网络传播

模型对疾病特征的表达以本次新型冠状病毒感染的肺炎（COVID-19）为基础，体现传染性、潜伏性、自限性等特征，采用流行病常用预测模型SEIR 模型的分类方法，将节点的感染状态分为易感（Susceptible）、潜伏（Exposed）、感染（Infective）、退出（Removal）四类[10]。

在模型中，疾病沿着两种不同的连接在节点之间传播，处于潜伏期和感染期的节点与易感节点的每一次交互都有一定概率将疾病传染给后者，长程连接和短程连接拥有不同的传染率βl 和βs，感染者具有潜伏期e 和康复率γ，疾病在潜伏期具有传染性。

2.4 公共卫生干预：各类防控措施的表达

从本次新型冠状病毒疫情来看，政府主要采取的防控措施主要包括3 大类：第一类是宣传教育类，主要包括疫情的及时通报和防护方法的普及，目的是引导市民调整个体行为（如戴口罩，减少聚会等）；第二类是监测类，主要包括在社区、公共设施和交通枢纽等地区进行体征指标监测（如体温测量）、要求市民定期上报健康状况等；第三类是隔离控制类，包括关闭城际交通、隔离疑似患者、小区封闭管理等，隔离控制具有显著的防控效果，但相应的经济和社会成本也比较高。

从模型表达来看，宣传教育类措施主要起到减少人际接触以降低传染概率的作用；监测类措施主要起到提前发现病患，从而缩短潜伏时间，加快感染者退出传播的作用；隔离控制类措施主要作用在于使节点间的长程连接和短程连接失效或减效，从而减少传染途径，不同类型干预措施的合理组合，能够高效而低成本地抑制流行病的传播扩散（图3）。

图3 公共卫生干预措施在模型中的效果

3 基于武汉的实证应用

湖北省武汉市是中国最早发现和确认新型冠状病毒肺炎的城市，同时也是国内受疫情影响最为严重的城市，自2019 年12 月8 日发现第一例不明原因的肺炎病例起，截止2020 年3 月20 日，武汉全市累计确诊50005 例，死亡2498 例。

3.1 初始条件设置

以武汉市主城区（三环线内）为对象（图4）构建基于智能体的流行病传播模型2），社群单元节点代表居住小区，短程连接代表社区影响范围内的日常活动，长程连接代表居住小区与城市主要中心之间的通勤和商业休闲活动（图5）。从武汉市新冠肺炎疫情防控指挥部社区疫情防控组2020 年3 月6 日公布的第一次无疫情小区评定数据可以推算（表1），武汉主城区的小区数量约为3776 个，根据武汉主城区的百度地图热力图一周平均数据对节点密度进行分配，总计建立3754 个社群单元节点，近似等于小区数量，并在此基础上按照小世界规则和偏好依附规则构建节点之间的短程连接和长程连接，假设初始感染者位置为武汉华南海鲜批发市场3）。

图4 武汉三环内区域的用地布局

表1 武汉主城区无疫情小区情况

3.2 公共卫生干预模拟

武汉疫情发展过程中，大量的防控措施对疾病的传播趋势起着重大影响，从公共卫生干预措施的时间分布来看，大致可以分为两个阶段：从发现第一例病患到2020 年1 月23 日武汉“封城”前，受到对新病毒认知和重视程度的限制，主要的防控措施为向公众告知疾病的发展情况和防护方法，引导市民戴口罩，勤洗手，远离密集人群等，由于宣传的力度是逐步提升的，而市民对信息的接受也需要时间，因此，这一阶段的公共卫生干预对控制疫情的影响是一个渐进的过程，在模型中表达为疾病通过连接传播的概率在逐日递减。随着疫情的扩散和中央政府的介入，自2020 年1 月23 日起，武汉先后实施了“封城”、“测温”、“隔离”、“住区封闭”等防控政策，公共卫生干预进入第二阶段，城市各节点之间的连接强度和数量、潜伏者被发现的概率都发生了显著的改变。为尽可能真实地模拟外部条件不断变化的情况下武汉疫情的传播情况，模型根据武汉防控政策实施的时间，对相关参数进行了相应的动态调整（图6）。

图6 武汉公共卫生干预措施对模型的影响

3.3 模拟结果

3.3.1 持续时间和感染总数

根据设定的条件对武汉市12 月8 日以来的疫情扩散情况进行模拟，疾病每天沿两种空间连接进行初始概率为βl和βs 的扩散，社群单元内的感染者自愈、收治和死亡情况均退出传播模拟，终止条件为被感染的社群单元数量降为0，主要考察数据为整个疫情的持续时间T 和感染总数C（图7）。传播参数设置主要在参照钟南山院士团队相关研究[5、11]的基础上进行了简化，取基本再生数R0=2.68，潜伏期e=7d，死亡率d=3%，康复率γ=0.14，接触传染概率b=0.05，并在此基础上根据长短程连接的频率和时长估算两种连接的传染率，最终取βl=0.35，βs=0.26。

图7 模拟结果（单次）

由于流行病的传播在数量上和方向上都具有随机性，单次模拟结果不具有代表性，故根据设定的初始条件和基于公共卫生干预的参数变化，对研究范围进行了500 次约束条件下的随机模拟，经清理后共计产生478 组有效数据4）（图8），可以看到由于模拟的初始病患的位置是确定的，因此数据总体离散度较小。根据随机模拟结果，疫情的持续时间平均值为90.8 天，与武汉疫情的实际持续时间102 天的偏差度为11.2%5）；受感染的社群单元总数平均值为2224 个，与根据统计数据所显示推算的感染居住小区数量2687 个的偏差度为17.2%6），显示基于智能体的城市流行病传播模型在模拟疫情扩散的持续时间和感染节点数量方面具有一定的准确性。

图8 500 次模拟感染总数结果

3.3.2 感染节点的空间分布

流行病在城市中的传播过程作为一个复杂系统，具有很强的随机性特征，从给定的初始条件无法推演出疾病在空间上扩散的唯一准确结果，但是通过统计500 次模拟结果中各节点的被感染的次数，可以推算整个疫情过程中城市不同空间位置上的社群单元被感染的概率（图9），进一步按照行政区进行分析并与由官方统计数据所推算的疫情中被感染的小区数据进行比较可以发现，模拟结果中感染概率均值最高的是汉阳区，最低的是武昌区（洪山区和青山区由于在模拟范围内的行政边界不完整，故未列入统计），各行政区的预测感染概率均值排序与从统计数据推算的各区疫情小区感染比例排序完全一致（表2），显示模型在对疫情传播空间分布的预测上具有较好的效果。

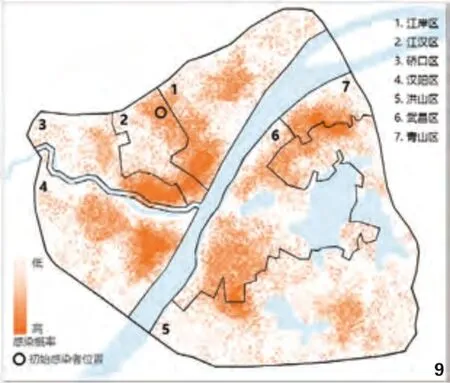
图9 城市空间感染概率分布

表2 各区感染概率比较

3.3.3 公共卫生干预效果

整个模拟过程中一共引入了五类不同的公共卫生干预措施来尽可能真实地表达武汉疫情发展的真实环境，具体包括：防疫宣传、交通停运、患者隔离、住区封闭和测温监控。比较不同干预措施条件下的疫情传播情况可以看到，各项措施在减少感染总数或缩短疫情持续时间方面均起到了相应的效果（图10），其中最早开始实施并贯穿整个传播周期的防疫宣传措施能够减少28%的感染总数；城市内外交通停运能够减少约10%的感染总数，并使整个疫情持续时间缩短20%；其后实施的感染者隔离控制、住区封闭管理、测温监控等措施亦能小规模地减少感染总数和疫情持续时间，起到巩固和稳定公共卫生干预效果的作用。总体而言，实施较早的措施，由于措施作用时间更长以及当时干预不足状态下疫情扩散较为严重等原因，对整个疫情发展趋势的影响十分显著；而在总体传播趋势已经得到控制后增加的干预措施对疫情的影响相对较小。

图10 不同公共卫生干预措施下感染总数曲线

为进一步考察公共卫生干预措施对疫情发展的影响，在同一个网络上对无干预措施的情景和所有干预措施提前10 天实施的情景分别进行了500 次模拟，结果显示无干预措施情景下感染节点总数的平均值为3246，而提前10天干预情景下感染节点总数的平均值为905，将这两组数据与实际情景（上文中按照武汉防控措施实际实施时间进行模拟的情景）进行对比可以看到，公共卫生干预措施会对控制流行病的空间传播范围产生巨大的作用，并且越早进行干预，对疫情传播的控制效果越显著（图11）。

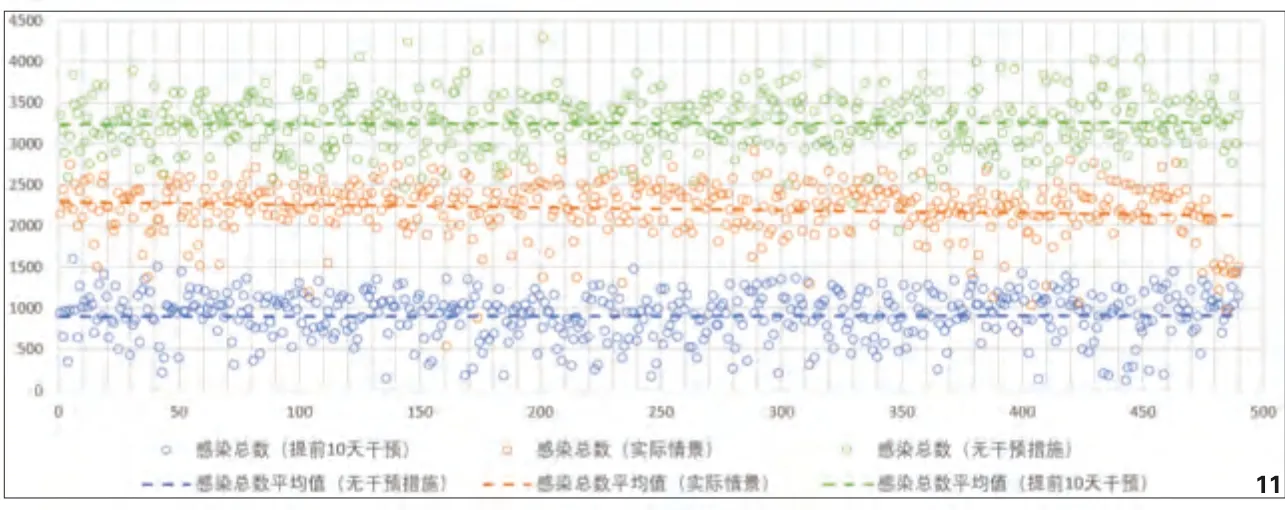
图11 三种情景下感染总数500 次模拟结果

3.4 一些影响结果的因素探讨

（1）模型中流行病传播的网络尽管是以真实的城市空间结构和住区、人口数量分布为基础，但还是做了大量的抽象，忽略了不同社群单元的人数差异、各节点间的非日常联系、干预措施在整个网络中执行的不均匀性、整个疫情期间城市内总人数的变化以及超级传播者存在的可能等，因此与实际的城市空间环境还是有着明显的差异。

（2）基于连接的传播主要模拟的是A、B 两点之间由于人群交换而产生的疾病传播，但没有考虑两点之间路程中的传播情况，事实上大城市中较为拥挤的公共交通造成的传染对整个城市疫情扩散的速度、规模和复杂程度都会产生重要影响。

（3）模型对各项公共卫生干预的表达参数置入时间是以相关政策文件的发布时间为准，事实上，有些政策的效果开始显现时间可能更早，因为在正式的政策发布之前，社区和市民就已经陆续开展一些相应的防控行为，如进出社区测量体温、主动减少出行等；而有些政策效果的全面实现时间则可能更晚，因为防控政策发布后不可能立刻生效，需要一定的人力和时间来逐级安排落实。

（4）模型运行的终止条件为全部感染者退出模拟，其中包括感染人员发病被送往医院救治并隔离的情况，因此模型对疫情结束的实际定义是病毒在医疗系统外的城市空间中消失，而实际情况下，从最后一例病患送达医院到医院中所有的病患全部康复还需要相当一段时间，这期间甚至还可能伴随医护人员的感染而产生新的病患，这些都会导致疫情的实际持续时间比模拟结果更久。

（5）2020 年3 月6 日发布的武汉第一批无疫情小区数据以2 月21 日起无病患为标准，考虑到还存在2 月21 日前康复的情况、2 月21 日后疑似排除的情况以及3月6 日后被感染的情况，由此推算的武汉主城区被感染小区数量与实际情况可能存在一些偏差。

结论与展望

基于智能体的城市流行病传播社群单元模型能够在表现城市空间结构的复杂网络上模拟流行病的自然传播过程以及公共卫生干预措施的实施效果，在预测疫情持续时间、感染节点总数及其空间分布方面表现出较好的精确度。与传统的流行病动力学模型相比，该模型的优势在于考虑了实际的城市空间和人群活动特征对疾病传播的影响，并且能够预测疫情扩散的空间分布，不足之处在于没有对社群单元内部传播的微观表达，在预测感染人群的具体人数时精确度有限。此外，以武汉市为例的新型冠状病毒疫情模拟还证实了公共卫生干预措施能够在很大程度上抑制疾病的传播，并且干预措施实施的时间越早，对疫情的控制效果越强，因此，畅通的信息传递渠道、快速的决策机制和高效的行政执行力是城市流行病传播干预和控制的关键要素。

本研究在空间尺度上主要讨论静态条件下的城市内部疫情传播情况，对于更宏观的城市人群流入和流出对疾病传播的影响，以及更微观的社群单元内部的传播机制均未作展开研究，后续拟逐次完善各个尺度层级的传播机制分析和模拟，形成贯穿“全球—全国—区域—城市—社群”各层面的流行病空间传播完整模型。

图、表来源

图1：http://icity.ikcest.org/content/covid19map.

图5、7、10：模型运行过程截图。

图6：根据武汉市新冠肺炎防控指挥部通告第1 号、5 号、6 号、7 号、9 号、10 号、12 号、15 号及相关新闻报导整理绘制。

图2～4、8、9、11：作者绘制。

表1-2：根据2020 年3 月6 日武汉市新冠肺炎疫情防控指挥部社区疫情防控组公布的全市第一次评定的无疫情小区、社区、村（大队）名单及本研究模拟结果整理绘制。

注释

1）Netlogo 是美国学者Uri Wilensy 于1999 年发起，并由美国链接学习和计算机建模中心（CCL）进行持续开发的一款多智能体模拟和编程平台。Netlogo 不仅具有很强的海量个体模拟能力，同时有着简洁友好的操作界面，近年来在国内城市研究领域颇受青睐，在人群疏散模拟、城市用地扩张模拟、商业中心体系模拟等研究中发挥了较为重要的作用[14-17]，但目前使用Netlogo平台和ABM 方法对流行病的空间传播进行模拟和研究的实践还比较少。

2）根据《武汉市城市总体规划（2010-2020）》，武汉主城区以三环线以内地区为主，同时还包括局部外延的沌口、庙山和武钢地区，总面积678km2，本研究为数据统计和模拟参数设置方便，选择三环以内作为模拟范围。

3）从疫情爆发后最初的病例报告看，武汉的华南海鲜市场一度被认为是疫情发源地，其后随着各国专家对于病例和病毒基因数据的深入分析发现该市场并非病毒和病例的发源地。研究考虑华南海鲜市场是最早发现的感染人数比较集中的地点，也是对武汉疫情传播影响最大的节点，因此仍选取华南海鲜市场作为模拟研究的初始节点。

4）清除的无效数据主要是疫情没有成功传播的情况，即初始病患还没有将病毒传染给其他人就自愈或死亡了，这种情况会出现在自限性疾病和高致死率传染病情景下，本研究对传染病的传播机理主要模拟新型冠状病毒肺炎COVID-19（自限性疾病），因而此类数据较多。

5）2020 年3 月19 日，武汉市新增确诊数量首次为0，距离2019 年12 月8 日发现首例病患经过了102 天。

6）2020 年3 月6 日至20 日，武汉市新冠肺炎疫情防控指挥部社区疫情防控组一共公布了6 批无疫情小区名单，具体评选标准为居住小区最近14 日内无确诊病例及疑似病例，由于3 月起武汉新增病例数逐渐下降，痊愈人数大量增加，无疫情小区数量也在快速增长，因此第一批名单对于推算武汉市区受感染小区数量最有参考价值。