光伏组件双二极管模型参数辨识混合方法研究

张国玉，王宏华，赵慧文

(1.南京工程学院工业中心，江苏南京 211100；2.河海大学能源与电气学院，江苏南京 211100)

随着不可再生能源的日益枯竭以及环境污染的日益严重，可再生能源发电逐渐成为各国关注的重点。太阳能因其资源丰富、清洁无污染等优势，成为国际认可的理想替代能源之一。太阳能的主要应用是光伏发电，光伏组件是光伏发电系统的核心，因此精确建立光伏组件的数学模型对光伏发电系统的理论研究具有重要意义[1]。

目前，用于描述光伏组件电流和电压特性关系的模型主要有单二极管五参数模型和双二极管七参数模型[2-3]。单二极管模型由于参数少、计算简单，已经成为工程上使用的主要模型。但是，不同的研究表明，双二极管模型更能准确地反映光伏组件的特性，尤其是在低光照条件下[2]。光伏组件模型参数辨识的方法主要有解析法[4-6]、数解法[7]和智能算法[8-10]。解析法和数解法都依托于I-U 特性曲线在关键点(短路电流、开路电压、最大功率点)处获得的等式方程。前者需要做一定的假设，或者忽略一些参数，求解简单、快速，但精度相对较低[3]。后者一般需要引入新的参数，如电压/电流温度系数、开路电压处的串联等效电阻、短路电流处的并联等效电阻，以构建新的方程，求解时对初始值敏感，容易陷入局部最优解甚至求解不出数值。智能算法虽然具有计算速度快、求解精度高等优点，但目前国内外学者大多数选用实际测量值与计算值的误差，如均方根误差作为评价指标[3,10]，只有在具备实验数据的基础上才能提取模型参数。

基于上述常用方法的优缺点，本文在不做任何近似处理的前提下，提出基于自适应混沌粒子群算法(adaptive chaotic particle swarm optimization，ACPSO)的光伏组件双二极管模型参数辨识的新型混合方法。对不同类型的光伏组件，在不同的运行条件下进行光伏特性仿真，通过实测数据、工程简化模型与本文模型结果的比较，验证了本文模型的有效性和精确性。

1 光伏组件双二极管模型

光伏组件双二极管模型的等效电路如图1 所示。

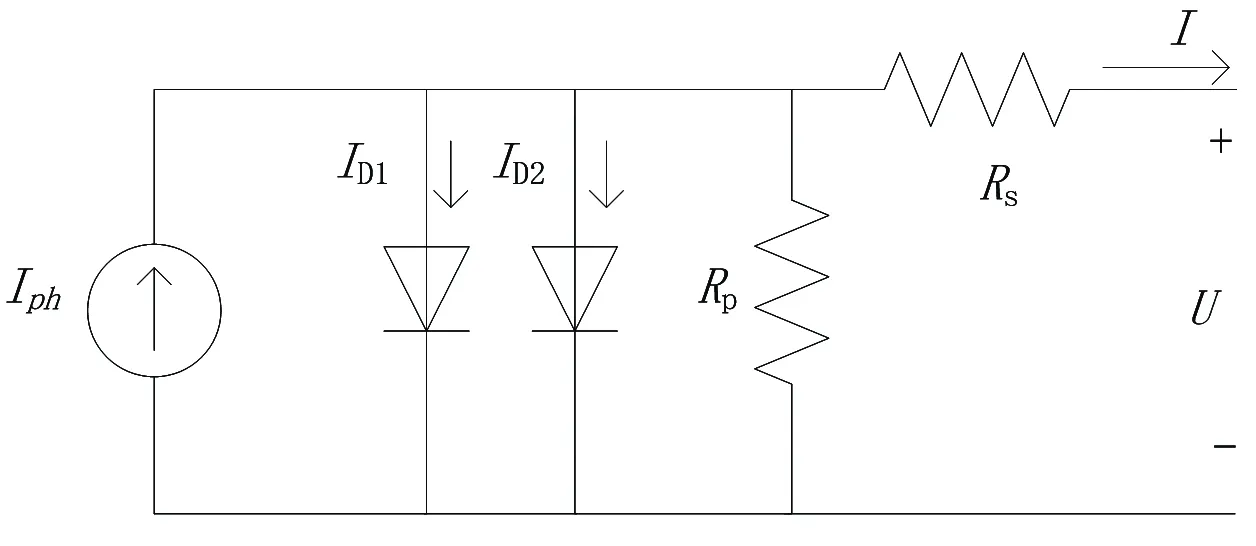
图1 双二极管模型等效电路

基于基尔霍夫电流定律，输出电流可表示为：

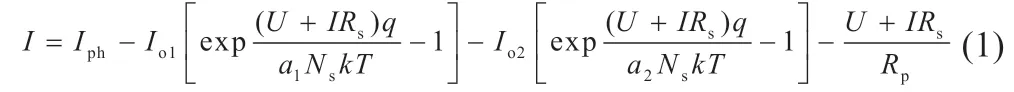
式中：I为光伏组件的输出电流；U为光伏组件的输出电压；Iph为光生电流；Io1、Io2为两个二极管的反向饱和电流；a1、a2为二极管理想因子；Ns为串联电池的数目；Rs、Rp分别为串联等效电阻和并联等效电阻；q为电子电荷量，1.6×10-19C；k为玻尔兹曼常数，1.38×10-23J/K；T为光伏组件的绝对温度。

2 双二极管模型参数数值求解

2.1 光照和温度变化下的模型参数计算

设Iphr、a1r、a2r、Io1r、Io2r、Rsr、Rpr为标准条件下光伏组件双二极管模型的参数值，Gr和Tr为标准条件下的光照值和温度值，分别为1 000 W/m2和25 ℃。考虑外界光照(G)和温度(T)的影响，可采用式(2)确定Iph、a1、a2、Io1、Io2、Rs、Rp的值。

式中：Ki为电流温度系数；Eg为禁带宽度。

2.2 标准条件下模型参数求解分析

设Iscr、Uocr、Imr、Umr为标准条件下的短路电流、开路电压、最大功率点电流和最大功率点电压。首先，在三个关键点：短路电流点(0，Iscr)，开路电压点(Uocr，0)和最大功率点(Umr，Imr)处分别代入式(1)，可得如下方程：

在T=Tx，G=Gr条件下，结合电压温度系数Kv、电流温度系数Ki及式(2)、式(3)可得[2]:

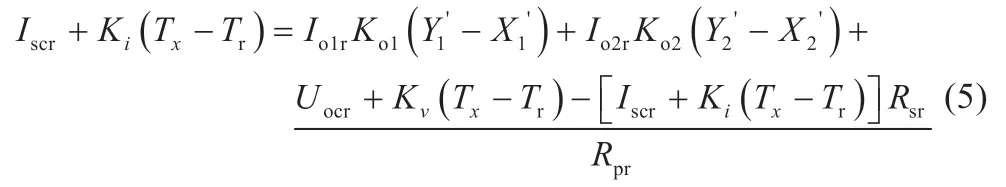
其中：

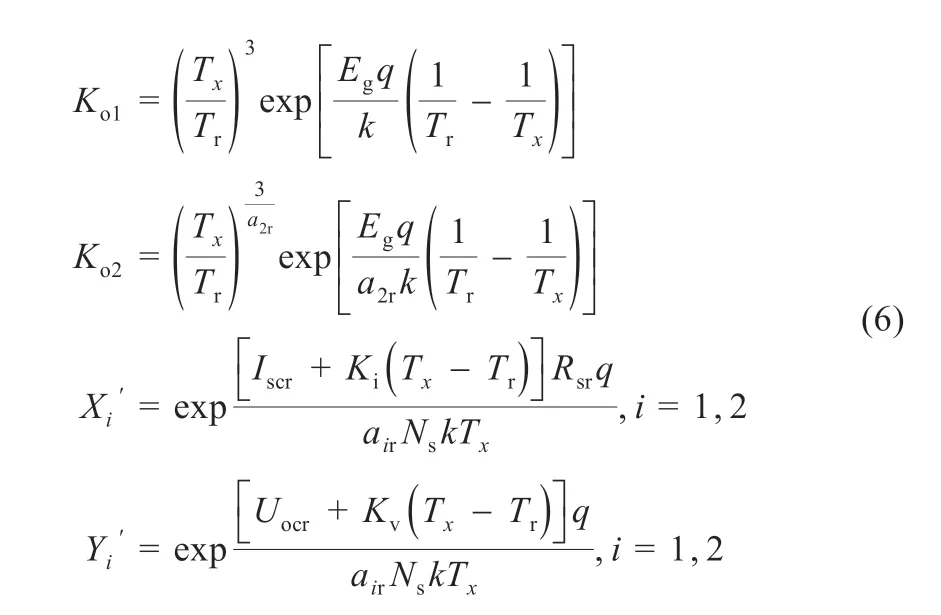
根据式(3)和式(5)，参数Iphr、Io1r、Rpr、Io2r可表示为a1r、a2r和Rsr的函数：

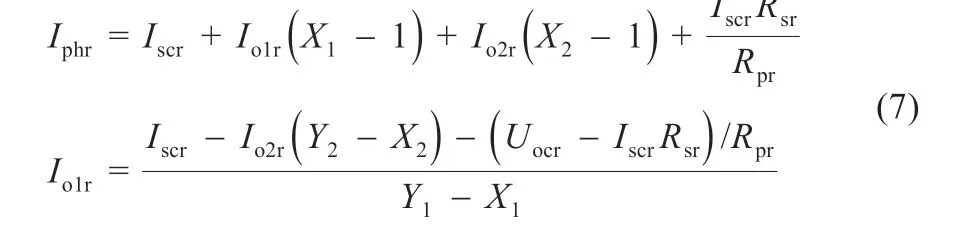
3 标准条件下基于ACPSO 算法的参数求解

3.1 理想因子上界取值策略

标准条件下，光伏组件双二极管模型理想因子a1r和a2r的取值范围一般分别设定为[1,2]和[2,4][9]，但实际上，a1r取值接近于1，a2r取值接近于2。本文为了使求解结果接近于实际值，理想因子的上界取值动态变化，即先设定一个较小的上界值，如果在该设定范围内无法求解出符合条件的解，继续增加上界值的大小，如此循环，直至能求解出符合条件的最优解为止。

3.2 适应度函数

采用ACPSO 算法求解a1r、a2r和Rsr参数时，必须建立一个用以评估每个粒子优劣的评价指标。基于此评价指标的适应度函数，算法完成个体极值和全局极值的更新，不断迭代以求解出最优解。通常选用实际测量值与计算值的误差作为评价指标，如均方根误差、平均绝对百分比误差，但是这需要预先测量出适量的实验数据。

基于在最大功率点状态下，功率对电压求导的导数为0，以及为保证算法最终求解的模型参数值均在取值范围内，选用式(10)作为评价指标的适应度函数，无需依赖于实验数据，模型适用性更广。

式中：当计算出的四个参数值Iphr、Io1r、Io2r和Rpr均在取值范围内时，flag取值为1，否则为0；F为适应度值；cons为一正常数，一般取较大值。

3.3 自适应混沌粒子群算法

ACPSO 算法的基本思想是在粒子群算法的基础上，在每一步迭代过程中，基于粒子聚集度自适应地引入混沌扰动，进行混沌局部搜索，引导粒子逃离局部最优区域以提高算法的收敛精度，同时更新一部分适应度值较低的粒子，保证种群的多样性。此外，使初始种群里至少存在一个可行解，用以加快算法的收敛速度和提高算法的求解精度；使惯性权重自适应动态变化，保证算法前期具有较强的全局搜索能力，后期具有较强的局部搜索能力。具体算法流程如下。

步骤1：设定算法参数，设定双二极管模型七参数的取值范围，随机初始化N个粒子的位置(a1r、a2r和Rsr)和速度，利用式(7)和式(8)求解双二极管模型的其余4 个参数值，利用式(10)计算每个粒子的适应度值。判断初始种群里是否存在可行解，如果全部为非可行解，则重新初始化N个粒子，若重复m次后仍全部为非可行解，则增加二极管理想因子的上界值，继续重复上面的操作，如此循环，直至初始种群里出现可行解为止。将初始种群每个粒子的适应度值设为个体极值，最小适应度值设为全局极值。

步骤2：通过式(11)更新自适应惯性权重、粒子的速度和位置，并对速度和位置进行越限处理。

式中：ω为自适应权重，ωmin、ωmax分别为其最小值和最大值；Fmin和Favg分别为最小适应度值和平均适应度值；c1和c2分别为个体学习因子和社会学习因子；r1和r2为[0,1]内随机数；k为迭代次数；分别为第k代第i个粒子的速度、位置和个体最优解；gbestk为第k代全局最优解。

步骤3：通过式(10)计算每个新粒子的适应度值，将每个粒子的当前适应度值和上次的个体极值进行比较，若当前适应度值优于上次的个体极值，则用当前粒子适应度值更新上次的个体极值。比较当前每个粒子的个体极值，得出当前迭代中的全局极值，若当前全局极值优于上次的全局极值，则用当前全局极值更新上次的全局极值。

步骤4：通过式(12)计算第k代种群的粒子聚集度δ及第k次迭代时引入混沌扰动的概率pk。

步骤5：在[0,1]内生成一个随机数，如果随机数小于混沌扰动概率，则转至步骤6，否则转至步骤10。

步骤6：将第n步混沌搜索时第i个粒子的个体最优解按照式(13)映射为0 到1 之间的混沌变量。

步骤7：采用Logistic 方程产生混沌序列，如式(14)。

步骤9：通过式(10)计算新个体最优解的适应度值，若优于原个体最优解，将新个体最优解作为局部搜索结果，同时更新个体极值和全局极值，否则返回步骤6 继续进行混沌局部搜索，直至达到搜索最大步数M为止。

步骤10：判断是否满足精度要求，若满足，跳到步骤11，若不满足，再次判断是否达到最大迭代次数，如果是，则增加二极管理想因子的上界值，迭代次数清零，返回步骤2，重复上面的操作，否则，直接返回步骤2，继续迭代搜索。

步骤11：输出全局最优解，得到a1r、a2r和Rsr的值，并利用式(7)和式(8)求解双二极管模型的其余4 个参数值Iphr、Io1r、Io2r和Rpr。

4 算例仿真及分析

4.1 标准条件下的模型验证

光伏组件双二极管模型参数均有一定的取值范围。其中，光生电流Iphr接近于短路电流Iscr，取值范围设为[0.95Iscr，1.05Iscr]；反相饱和电流Io1r、Io2r的值均不超出短路电流Iscr值的10%，且Io2r的值大于Io1r；串联等效电阻Rsr和并联等效电阻Rpr的取值范围分别设定为[0.01,3]和[50,3 000]。此外，Tx为一偏离标准温度较大的值，设为75 ℃。

ACPSO算法的参数设置如下：种群规模N为20，重复初始化最大次数m为100，ωmin、ωmax分别为0.4 和0.9，c1和c2均为1.494 45，最大迭代次数maxgen为1 000，调节概率变化快慢参数α为3，混沌搜索最大步数M为5。为了验证本文所提参数辨识混合方法的有效性和精确性，选取三种不同类型的光伏组件，对其在标准条件下的模型精度进行验证，并与文献[4]中方法1 进行比较(标准条件下方法1 和方法2 等同)。三种不同类型的光伏组件分别为单晶硅SP75、多晶硅MSX60 和薄膜电池ST36，表1所示为各光伏组件的电气参数。

表1 光伏组件的电气参数

表2 给出了标准条件下a1r、a2r和Rsr的计算结果及均方根误差(RMSE)的对比。图2～图4 分别显示了三种光伏组件的电流绝对误差对比曲线。可以看出，本文模型精确性优于工程简化模型，电流绝对误差均低于0.1 A。这主要归因于两方面，一是本文模型未做任何近似处理，二是双二极管模型的求解精度优于单二极管模型。

表2 参数辨识结果及均方根误差的对比

图2 SP75电流绝对误差曲线

图3 MSX60电流绝对误差曲线

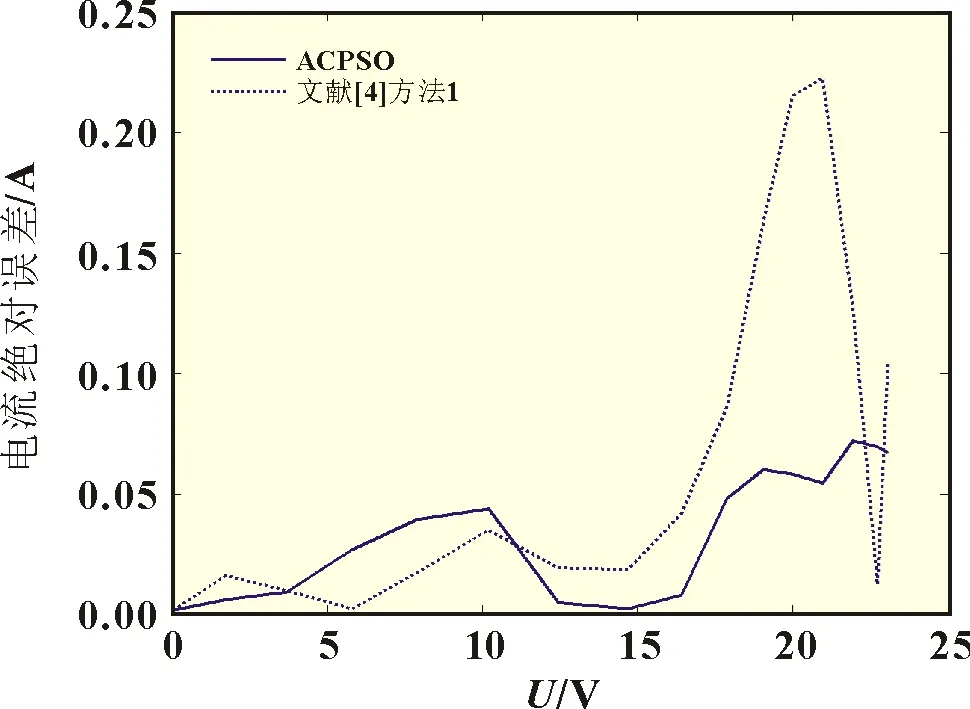
图4 ST36电流绝对误差曲线

ACPSO 算法是一种随机搜索算法，每次运行结果并不完全一致。为了验证算法的一致性，需要多次运行并进行统计分析。表3 给出了算法运行30 次各光伏组件参数辨识结果的平均值和标准差值。可以看出，a1r、a2r和Rsr参数的标准差值都特别小，均低于0.05，这表明每个参数的运行结果都在一个很集中的区域内。

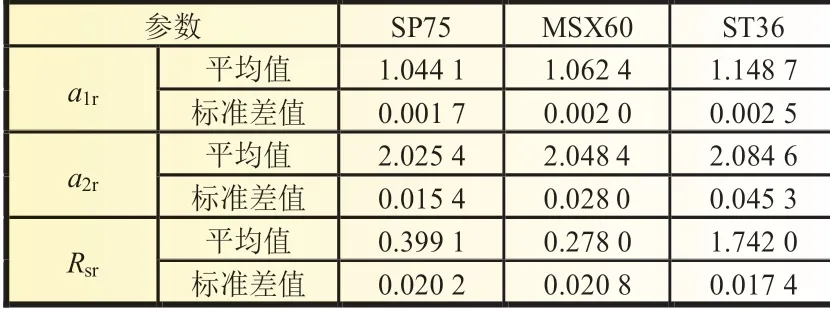
表3 参数辨识结果的平均值和标准差值

4.2 光照和温度变化下的模型验证

以单晶硅SP75 为例，验证本文模型在光照和温度变化下的精度，并与文献[4]中两种方法的结果进行对比。图5 显示了在不同光照，温度恒为25 ℃的运行条件下，SP75 的仿真I-U 曲线和测量I-U 曲线。图6 显示了在不同温度，光照恒为1 000 W/m2的运行条件下，SP75 的仿真I-U 曲线和测量I-U 曲线。表4 列出了各方法的均方根误差。结果表明，本文模型在光照和温度变化下同样适用，均能较好地拟合实验数据，拟合效果优于文献[4]的两种方法。

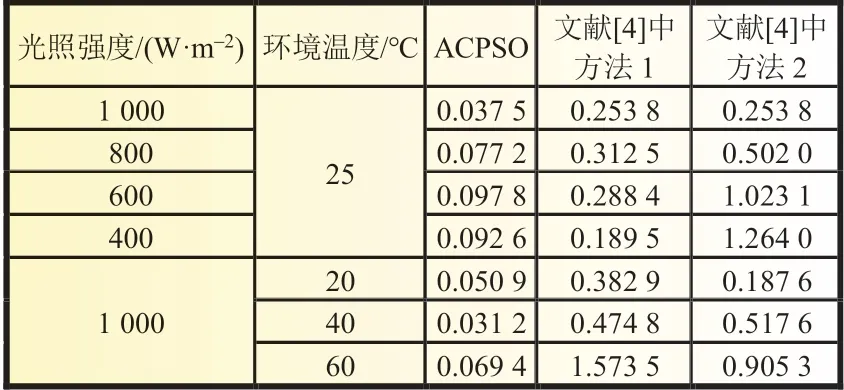
表4 均方根误差对比

图5 不同光照下SP75的I-U特性曲线

图6 不同温度下SP75的I-U特性曲线

5 结论

在不做任何近似处理的前提下，本文提出了一种双二极管模型参数辨识的新型混合方法。在标准条件下，基于ACPSO 算法与解析法相结合的应用，先优化求解a1r、a2r和Rsr的值，再利用解析法求解Iphr、Io1r、Io2r和Rpr的值，最后结合模型参数随温度和光照的变化关系，求解出一般工况下模型的各个参量。仿真结果验证了本文方法对不同类型的组件，在不同的运行条件下都能有效地进行参数辨识，模型精度均优于工程简化模型，可用于光伏系统的建模设计。