基于电池老化的并联式HEV能量管理策略

张世义，王清宇，李 军

(1.重庆交通大学航运与船舶工程学院，重庆 400074； 2.重庆交通大学机电与车辆工程学院，重庆 400074 )

电池老化给整车能量控制带来的影响是混合动力汽车(HEV)有待解决的问题[1-2]。对于整车能量管理策略而言，等效燃油消耗最小控制策略(ECMS)根据工况计算发动机和电机的各种转矩分配，以及转矩组合下的整车性能，确定最佳的转矩分配，可以降低能耗。苗强等[3]采用动态规划算法求得权重因子，针对单轴并联式HEV，设计一种自适应ECMS，整车油耗相比动态规划算法在荷电状态(SOC)未达到电量维持状态减少了3.2%，在稳定阶段(电量维持水平状态)减少了0.1%～0.2%。邓涛等[4]以最优扭矩分配为目标，在动态规划算法的基础上提出了一种改进瞬时ECMS，燃油经济性提高了3.2%。解少博等[5]分别应用动态规划、ECMS和自适应ECMS等进行仿真实验，发现自适应ECMS的控制效果更好。石琴等[6]在ECMS控制策略基础上，提出一种基于多目标粒子群算法的ECMS控制策略，与传统ECMS算法相比，油耗降低了10.28%。

在对HEV能量管理策略的研究中，ECMS都表现出了不错的效果。李旭玲等[7]提出了一种减小锂离子电池SOC区间并降低高SOC时充电电流的方法，使容量衰减率降低了15.6%，充放电过程中的放电总容量提高了23.07%。G.Suri等[8]利用电池老化模型构建了严重度因子图，用于衡量电池在不同运行条件下的相对老化情况，结合HEV模拟器进行仿真，将整车经济性提高了4.6%。

此前的研究只是单独对电池模型或能量管理策略的研究，未将电池老化作为优化燃油经济性的控制变量。本文作者针对电池老化问题，考虑老化对锂离子电池充放电能量效率[9]的影响，建立老化模型，提出一种以电池退化和能耗最小为目标的自适应ECMS控制策略，并进行了验证。

1 动力学模型

1.1 电池模型

电池组采用的是开路电压和电池内阻随电池状态实时变化的Rint模型，表示为：

(1)

(2)

(3)

1.2 发动机模型

汽车发动机作为并联式HEV的主要动力来源之一，效率是由转速和转矩决定的。对于HEV，发动机的燃油消耗Qg可作为控制策略设计的优化性能指标，计算公式为：

(4)

式(4)中：Pe为发动机的功率(kW)；b为燃油的消耗率[g/(kW·h)]；ρ为燃油的密度(kg/L)；g为重力加速度；Te为发动机的转矩(N·m)；ωe为发动机的转速(r/min)。

1.3 电机模型

并联式HEV中，电机工作效率(ηm)由电机转速(ωm)和转矩(Tm)决定，计算式为：

ηm=f(Tm,ωm)

(5)

1.4 纵向动力学模型

采用准静态建模方法建立双轴并联式HEV动力学模型，车轮处需要的动力根据车辆行驶动力学公式计算。各项参数如表1所示。

表1 动力系统参数

2 电池老化模型

电池老化是一个不可逆的过程。导致这种不可逆变化的机制包括：电池内阻增加；电池充放电过程中一些不可逆化学变化，导致Li+不断被消耗；化学反应消耗活性物质。老化是电池寿命缩短的主要因素，主要表现为容量的损失，其中固体电解质相界面(SEI)膜的增厚是容量衰减的主因。

2.1 电池循环老化模型

循环老化是电池反复充放电导致容量损失的一种表现。经过大量循环老化试验，人们开发了以控制为导向的电池循环老化模型，计算式为[10]：

(6)

式(6)中：Qcyc为电池循环老化容量损失；α和β为拟合系数；SSOC为电池剩余电量；Ea为活化能，31 500 J/mol；Crate为电流速率；η为Crate的补偿因子；R为摩尔气体常数；TK为电池测试时的环境温度(K)；QAh是电池充放电总电量；z为幂律因子，0.57。

为了量化实际循环中的老化效应，重要性因子σ表示为：

(7)

式(7)中：Ah′nom为电池结束寿命前总的充放电容量；常温测试工况下，定义SSOC，nom为0.35；Creat′nom为0.25C；TK′nom为298.15 K；Ah′cyc表示充放电总容量达到一个真实的电池运行状态(电池充放电过程中总的充放电容量近似真实状态)；Qcyc′e为电池寿命结束前循环老化的容量损失，该值与日历老化密切相关，无法事先得到，需根据工程经验进行估算，约为15%。

根据重要性因子的概念，有效的充放电总容量可以定义为[10]：

(8)

式(8)中：t为整个工况时间；τ为电池充放电时间。

有效充放电总容量是衡量电池内部电荷交换所导致的有效循环寿命消耗。最小化有效充放电总容量可优化循环老化导致的容量损失。动态循环老化的离散时间方程为：

(9)

式(9)中：下标k和k+1分别表示第k和k+1时刻。

2.2 电池日历老化模型

SOC和工作时的温度是造成电池日历老化的主要原因，因此，电池的日历老化模型可表示为[11]：

(10)

式(10)中：Qcal为日历老化引起的容量损失；T为电池温度；t为时间年限。

3 优化方法

实验研究的最优控制目标函数包括汽车能耗最小和伴随的电池老化成本最小，因此，结合Pontryagin最小值原理(PMP)算法，采用双状态自适应ECMS建立目标函数。

3.1 PMP算法

基于PMP算法的插电式HEV能量管理的基本原理为：在已知动态条件下，求解性能函数的最小值问题。该问题可转换为满足边界条件的哈密顿函数最小值问题。为跟踪最佳电池容量退化，引入状态变量QAh′e，性能函数表示为：

(11)

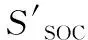
λ0(t)的动态方程可表示为：

(12)

(13)

边界约束条件如下：

(14)

式(14)中：Ichg、Idis分别是电池充电电流和放电电流；e、m分别代表发动机和电机的约束条件。

3.2 自适应ECMS算法

为了跟踪最佳电池容量退化，由式(12)、(13)可得，哈密顿函数可表示为：

(15)

式(15)中：λ1(t)是QAh′e的协态变量；为理想权重因子。

利用SOC和容量同时作为双状态自适应ECMS算法的状态量，因此引入等效因子α0和等效因子α1，建立每一瞬时的等效油耗函数[F(t)，优化流程见图1]，函数可表示为：

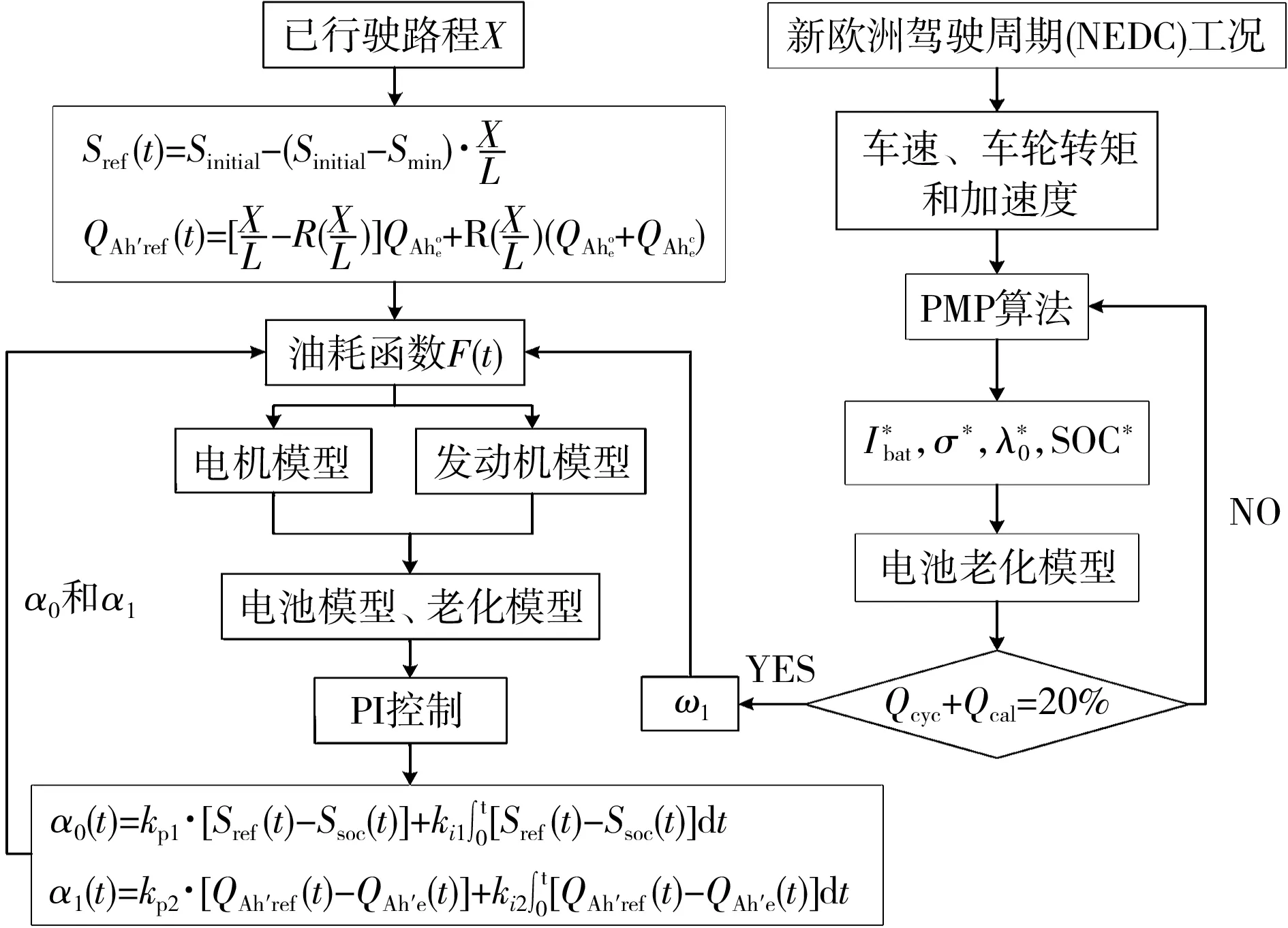
图1 优化流程图

(16)

式(16)中：mf为整个工况的油耗。

4 仿真结果及分析

4.1 仿真结果

为研究电池老化对HEV燃油经济性的影响，在提高燃油经济性的同时延长电池寿命，采用NEDC工况(见图2)，结合建立的整车模型，采用准确的电池日历寿命，基于Pontryagin最小值原理，计算确定权重因子ω1=3(见图3)。分析电池老化与能源消耗之间的作用，并在优化框架中体现电池老化模型。观察电池SOC和容量损失轨迹，分析电池老化对HEV能量分配和燃油经济性的影响。

图2 新欧洲驾驶周期(NEDC)工况

图3 权重因子(ω1)对容量损失的影响

4.2 仿真结果分析

仿真过程中电池SOC的变化曲线见图4。

图4 电池SOC的变化曲线

从图4可知，在考虑电池老化模型后，为降低电池的容量损失和有效充放电总容量，电池强放电时，会适当减少放电，降低电池的输出电流；同时，增加电池老化模型后的SOC轨迹变化更加平缓，能合理实现SOC的规划，SOC终值提高了0.02，减缓了电池老化速度。

在整个仿真周期中，电池的有效充放电总容量见图5。

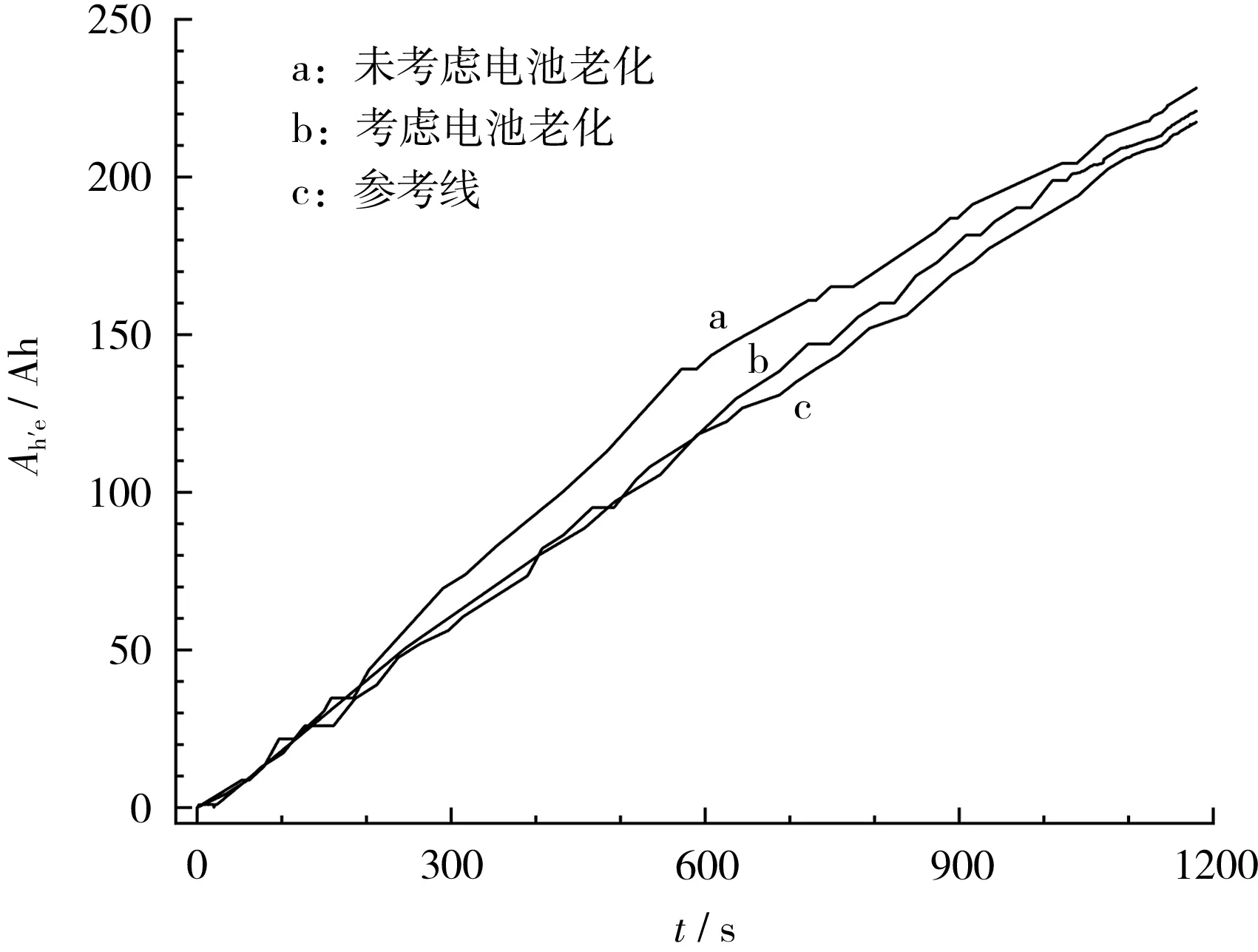
图5 电池有效充放电总容量

从图5可知，未考虑和考虑电池老化模型后的能量管理策略，所消耗的有效充放电总容量都大于参考值。考虑了电池老化模型后的有效充放电总容量，明显低于未考虑电池老化模型的，并且考虑电池老化模型后的有效充放电总容量更接近于参考值。与未考虑电池老化模型相比，考虑电池老化模型的有效充放电总容量降低了3.20%。

仿真过程中的电池容量损失见图6。

图6 电池容量损失

从图6可知，考虑电池老化模型后电池的容量损失，低于未考虑电池老化模型。仿真结果表明，考虑电池老化后的电池容量损失，比未考虑电池老化的降低了2.33%。

电机输出转矩见图7。

图7 电机瞬时输出转矩

从图7可知，与未考虑电池老化模型相比较，考虑了电池老化模型的策略会限制电机的峰值转矩，适当减少电机的峰值输出转矩，使电机处于高效工作区。

仿真过程中发动机的输出转矩及瞬时油耗分别见图8、图9。

从图8可知，与未考虑电池老化模型的结果相比，发动机的输出转矩在最优工作区间内得到合理提高。从图9可知，考虑电池老化情况后的瞬时油耗有所降低。实验结果得出(见表2)，考虑电池老化模型后的总油耗比未考虑电池老化的降低了1.25%，提高了经济性。

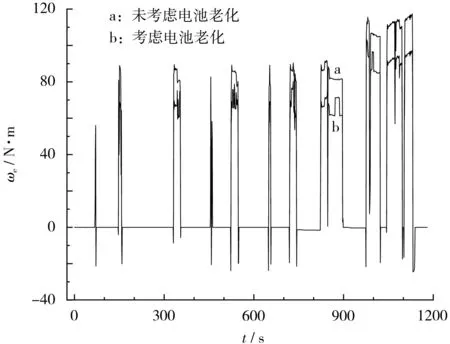
图8 发动机瞬时输出转矩

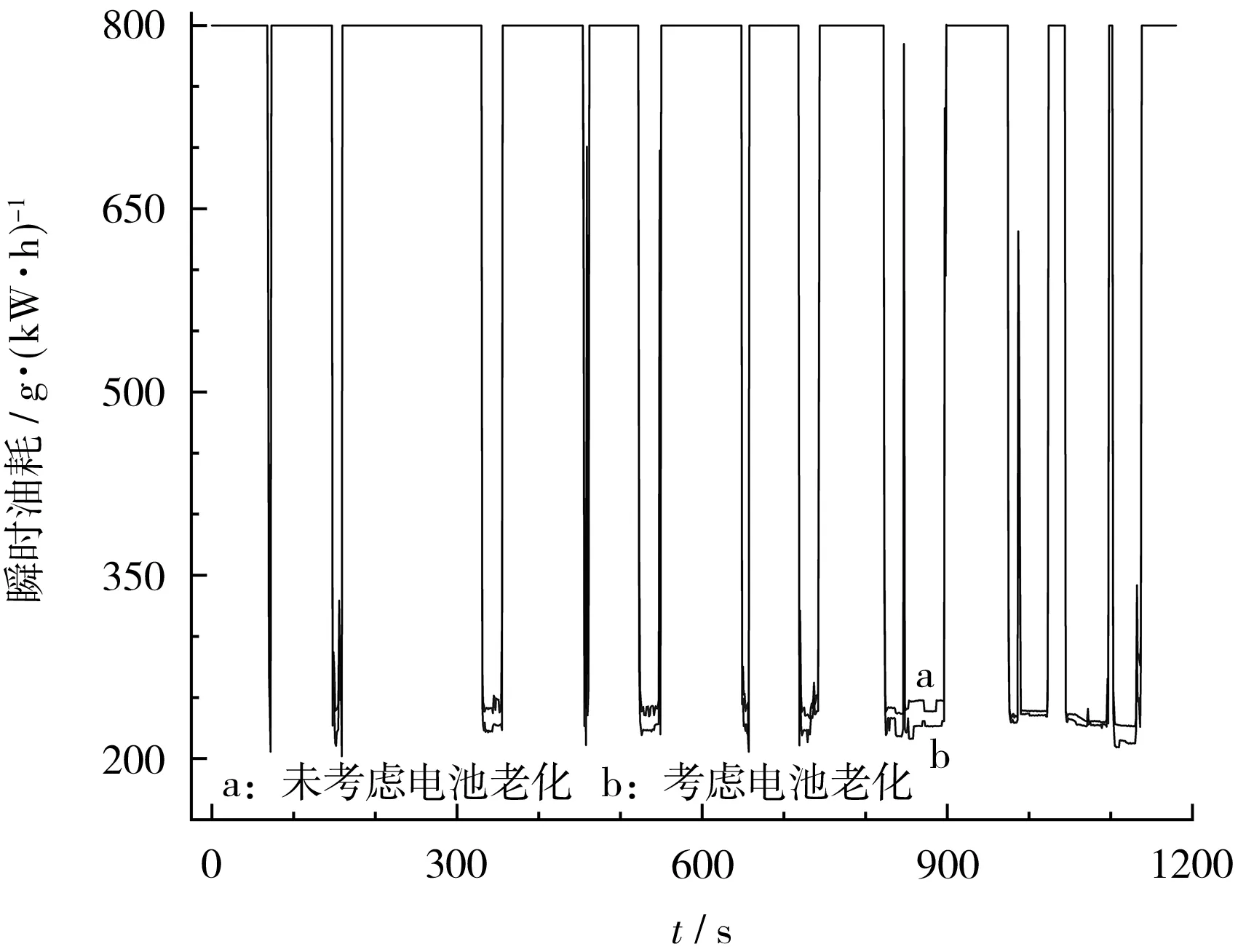
图9 整车瞬时油耗

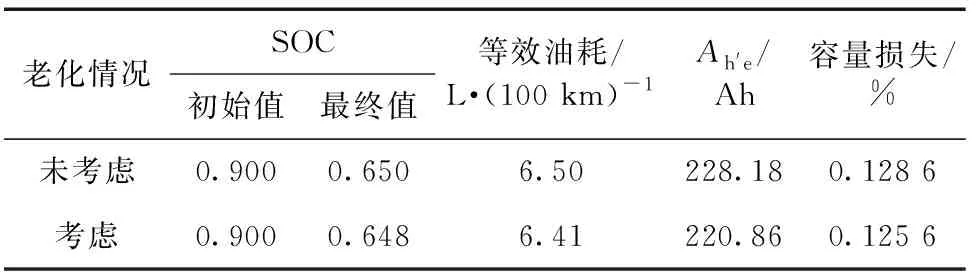
表2 整车经济性比较

5 结论

此前的研究，未将电池老化问题作为优化燃油经济性的准则，也未将电池老化模型加入整车模型中。本文作者基于MATLAB仿真软件，针对电池老化问题，建立电池循环老化模型和日历老化模型，并基于Pontryagin最小值原理，提出以能耗和电池老化同时最小的自适应ECMS控制策略，研究电池老化对整车能量控制的影响。仿真结果表明：考虑了老化情况的电池，有效充放电总容量减少了3.20%，电池容量损失降低了2.33%，同时仿真过程的总燃油消耗降低了1.25%，达到了同时降低油耗和减缓电池老化的目的。通过研究电池老化对整车经济性的影响程度，验证了该方法的有效性。