基于因子分析与改进K-means聚类的交通状态判别

高艳艳，陈秀锋，曲大义，陈 伟

(青岛理工大学 机械与汽车工程学院，青岛266525)

随着我国经济水平的提高，汽车保有量迅速增加，城市交通拥堵接踵而至。及时、准确地提供道路交通状态信息，出行者可以根据有效信息选择合适的交通工具以及出行时间点；交通组织者可以获取实时道路交通状态，采取交通控制和诱导对策，从而有效提高城市出行效率，缓解路网交通拥堵。

目前，交通状态判别主要从两方面开展：判别指标、判别方法。城市道路交通状态的判别指标主要有流量、速度、占有率、密度和平均延误等[1-3]，关伟等[4]对不同密度下的交通速度分布特性进行综合分析，最终把一个城市道路交通流划分为4种状态；戴学臻等[5]选取的判别指标为车辆平均行程车速、道路网延误时间比，利用集对化的分析方法与三角模糊化函数方法进行实时耦合，构建了城市道路交通运行状态识别模型；黄艳国等[6]选择了3个样本数据信息：流量、速度、占有率，并明确提出了一种道路交通运行状态实时化的判别分析方法，这种判别方法采用的是模糊C均值聚类算法。K-means聚类算法是判断城市道路状况最常用的方法之一，然而，由于聚类数的确定难度大，对初始聚类中心选择更是无统一标准，最终导致交通状态判别结果与实际城市交通状态不相匹配，这就需要对聚类数和聚类中心进行优化。针对这些问题，FAYYAD U等[7]明确提出选择多次迭代来更新采样数据以获得初始值，从而解决K-means算法严重依赖于初始聚类中心选择的问题；卞彩峰等[8]采用粒计算，这一算法属性分辨能力较强，利用这一优点，使聚类有效性函数对属性值依赖降低，最终获取最佳聚类数。

交通流参数选取具有一定的随机性，往往会影响判别结果的准确性。K-means聚类算法在一定程度上取得了实际效果，不过只是对聚类数和初始聚类中心进行单一优化，并未将两者结合在一起，仍存在一定的不足。本文利用因子分析方法，对多个变量进行相关性分析，选取出合适的交通流参数，作为交通判别指标，并结合改进K-means聚类算法，探究交通流的运行情况，从而对城市快速路交通状态进行判别。

1 数据采集及指标的选取

1.1 数据的采集与处理

本文所研究的对象是某城市约10 km快速路，交通流数据由两部分组成：①感应线圈检测器进行采集分析得到，包括流量q、速度v、占有率o。数据采集时间为某一个工作日0：00—24：00，每次数据采集时间间隔为5 min。该路段上某一截面命名为S，共有4条车道，每条车道上各有一个感应线圈检测器，分别为S1，S2，S3，S4。数据类型如表1所示。②行程时间t数据，利用Vissim仿真软件，根据实测数据进行标定得到。

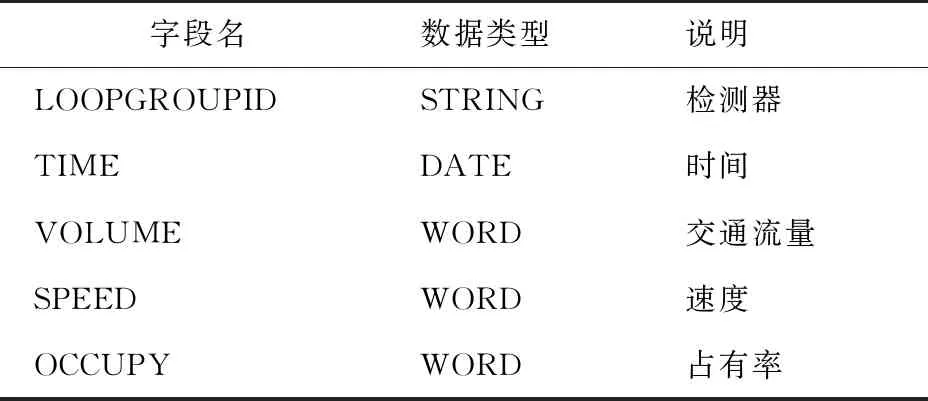
表1 数据类型

感应线圈检测器共收集原始数据852条，缺失12条，为了保证结果更加准确，现需要将缺失数据进行补充完整，数据具体处理方法如下：

1) 缺失数据的补充。由于本文数据仅缺失12条，属于少量数据缺失范畴，数据采集时间间隔较短，所以行驶状态不会发生太大的变化，基于以上特性，为保持数据的完整性，同时也要求计算简单，收敛性好，故采用分段线性插值法对数据进行补充。

分段线性插值法采用的函数是分段线性插值函数，用直线将两个相邻的数据点连接。要求一个点的数值，假设与其相邻的两个节点是(xm,ym)和(xn,yn)，具体求值方法如式(1)所示。

(1)

2) 数据的合成。本文数据是由4个车道所测数据组成，需要将每个车道上的数据合成为一个截面的数据[9]，合成数据方法如式(2)所示。

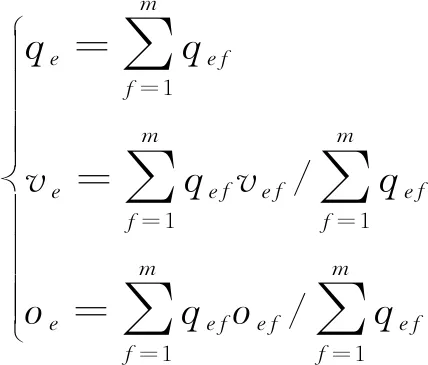
(2)

式中：qe为截面e的流量；ve为截面e的速度；oe为截面e的占有率；f为车道编号；m为截面车道数。

1.2 交通流参数的选取

交通流参数的选取和算法的应用效果密切相关，选择的交通参数要能够准确反映交通状态变化规律。结合交通流数据来源以及特点，本文选取8个交通流参数，分别为流量q、速度v、占有率o、密度k、行程时间t、饱和度s、占有率/流量(o/q)、占有率/速度(o/v)，其中q，v，o通过合成公式(2)计算得到，k，s，o/q，o/v在原有数据基础上，通过计算和处理得到，行程时间t由Vissim仿真获得。

2 因子分析

所谓因子分析，就是保持原有信息不发生任何的变化，将具有相同特性的变量划分到同一个因子中，实现数据的简化、指标的降维，从而简化因子分析过程[10]。

2.1 因子可行性验证

本文采用KMO(Kaiser-Meyer-Olkin)和Bartlett球形(Bartlett's Test of Sphericity)两种检验方法，检验8个交通流参数是否适合因子分析[11]。使用Spss软件进行检验，结果如表2所示，KMO结果为0.790>0.6，表明8个交通流之间存在较好的相关性。Bartlett球形假设检验显著性为0，拒绝零假设，表明相关系数矩阵不是单位阵，适合进行因子分析。

表2 KMO和Bartlett检验结果

2.2 主因子的提取

主因子提取通常采用不小于85%的累积方差贡献率来确定主成分的数量。如表3所示，前2个主因子累积方差贡献率为98.052%，大于85%，符合判断标准。因此，选取前2个主因子进行分析。

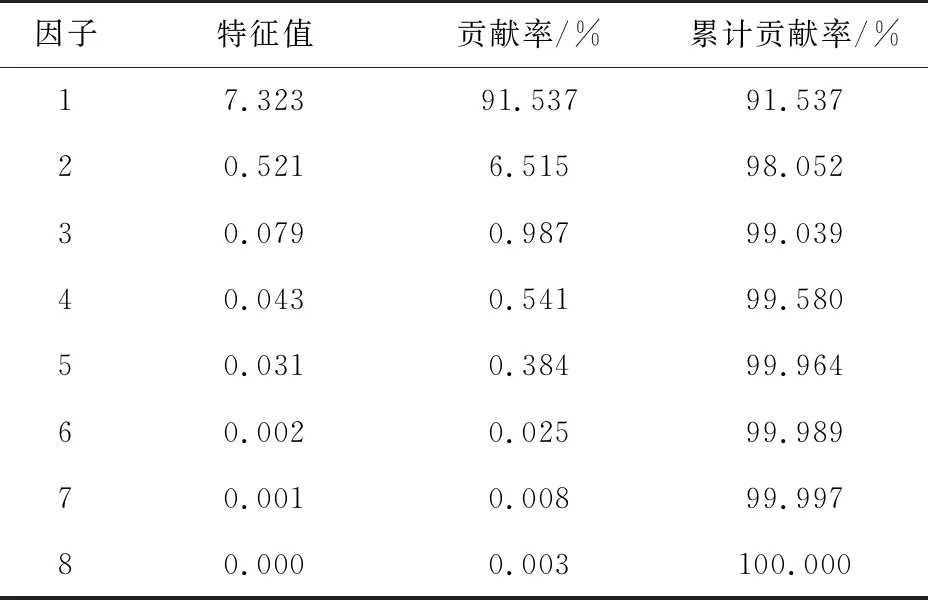
表3 各因子解释原有指标总方差情况

表4所示为因子载荷矩阵，显示出2个主因子在8个交通流参数上的载荷，通过分析得出以下个结论：

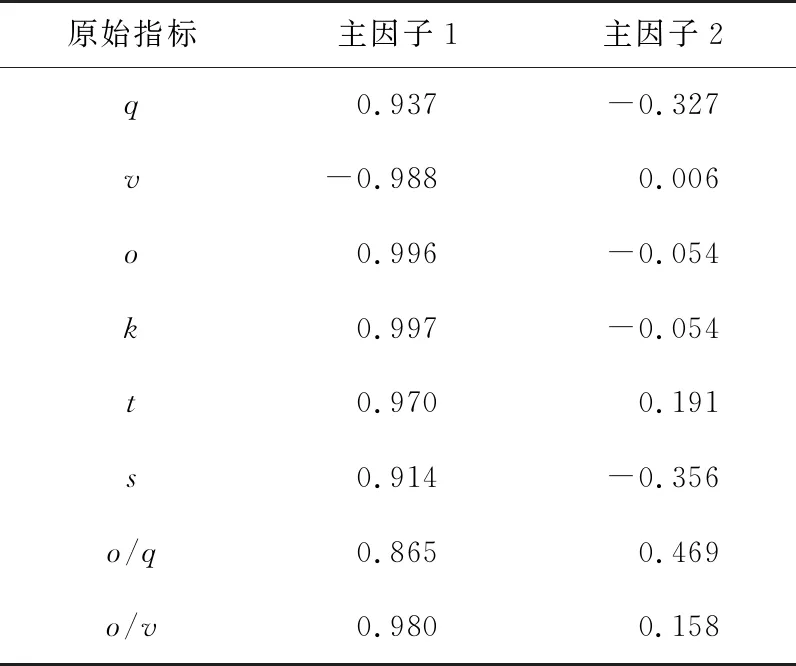
表4 主成分载荷矩阵

1) 主因子1与8个交通流参数的相关性均在0.8以上，此数据显示，主因子1与各交通参数都具有很强的相关性。无论是负相关还是正相关，为了符合实际，需进行因子旋转。

2) 主因子2与q、s、o/q相对于其他指标具有较强的相关性。

2.3 因子旋转

本文采用凯撒正态化最大方差法对2个主因子进行因子旋转。表5所示为因子旋转后主因子1，2对8个交通流参数的载荷。

由表5可知，旋转后的主因子1与q，v，o/v相关性较大；旋转后的主因子2与8个交通参数指标相关性还是很弱，综合考虑，剔除主因子2，仅保留主因子1。综上所述，因子分析从8个交通流参数中最终提取出q，v，o/v3个交通参数作为交通状态判别指标。

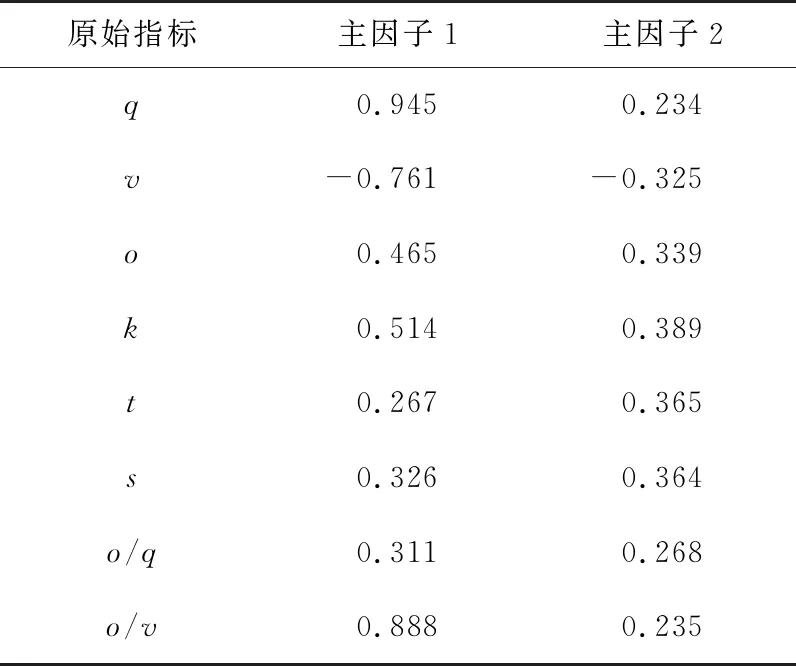
表5 旋转后的因子载荷矩阵

3 基于改进K-means聚类的交通状态判别

3.1 改进K-means聚类算法

K-means聚类算法根据样本之间的距离或相似度，把相似度高、差异小的样本聚类为一类，最后形成多个类别，使得同一个类别内的样本具有高相似度，不同类别间差异性大，聚类速度快，方法简单。但传统的K-means聚类算法仍存在一定不足：①聚类数K很难确定；②初始聚类中心选取随意。为了解决以上问题，本文提出了一种改进K-means聚类算法。

改进K-means聚类算法的思路如下：假设要将n个样本数据Y={Yi|i=1,2,...,n}划分为K类，用B={Bj|j=1,2,...,K}分别表示K种交通状态，C1点为首个初始聚类中心点，C={Cj|j=2,3,...,K}为后续初始聚类中心。

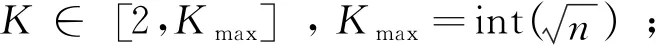
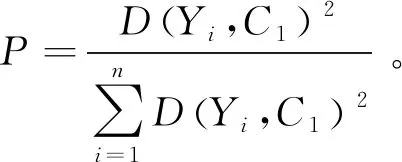
Step3：求出每个数据与初始聚类中心的距离D(Yi,Cj),i=1,2,...,n,j=1,2,...,K，根据求出的距离，按照距离最短原则，将每个数据归到相应的类别中，即满足D(Yi,Cj)=min{D(Yi,Cj)}，则Yi∈Zj；

Step7：通过指标值比较选择最佳的K值，使IDB指标达到最优；

Step8：输出最优聚类数K以及满足聚类准则函数收敛性的K个聚类集。

3.2 交通状态分类及判别效果分析

将改进K-means算法应用到处理好的289组交通流参数数据中，通过因子分析提取q，v，o/v3个判别指标，计算出初始聚类中心，最后输出最佳聚类数K=4，如表6所示，参照相关已有研究成果将交通运行状态命名为自由流状态、稳定流状态、拥挤流状态和阻塞流状态[12]。

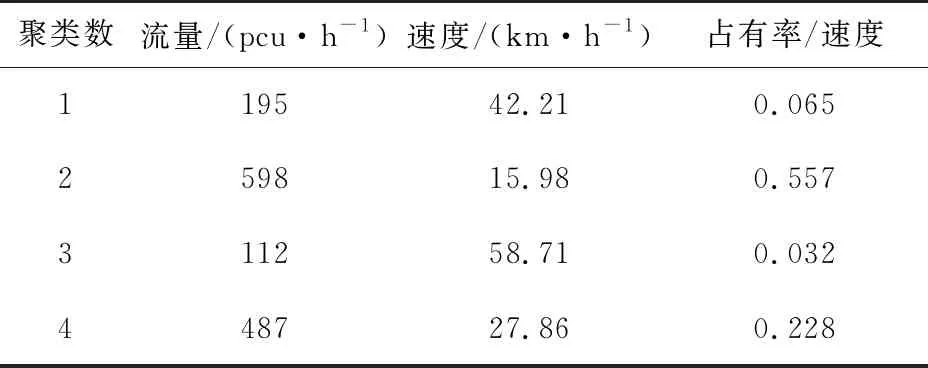
表6 初始聚类中心

使用Spss软件对数据进行交通状态判别分析，选取初始聚类中心，设置K=4，经过16次迭代，聚类中心的变化可忽略不计时，从而达到聚合的目的，将所有的数据划分为4类。表7所示为最终聚类中心。图1所示为截面S通过Spss检验最终得到的全天24 h交通状态判别结果，图2所示为Origin绘制的4种交通状态下的交通流基本参数关系。

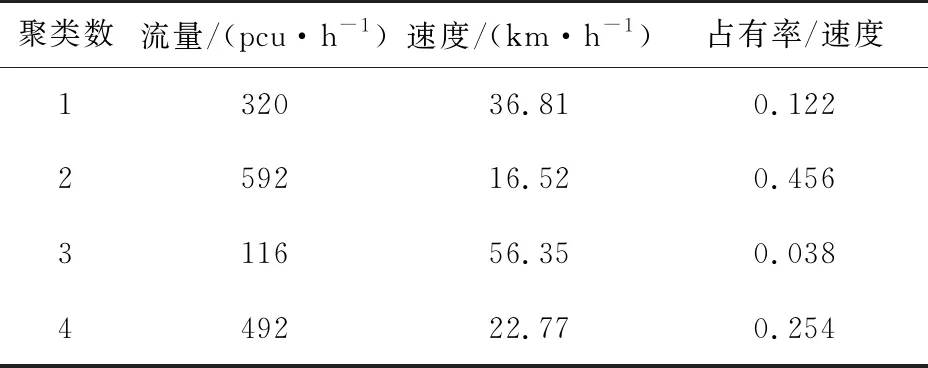
表7 最终聚类中心

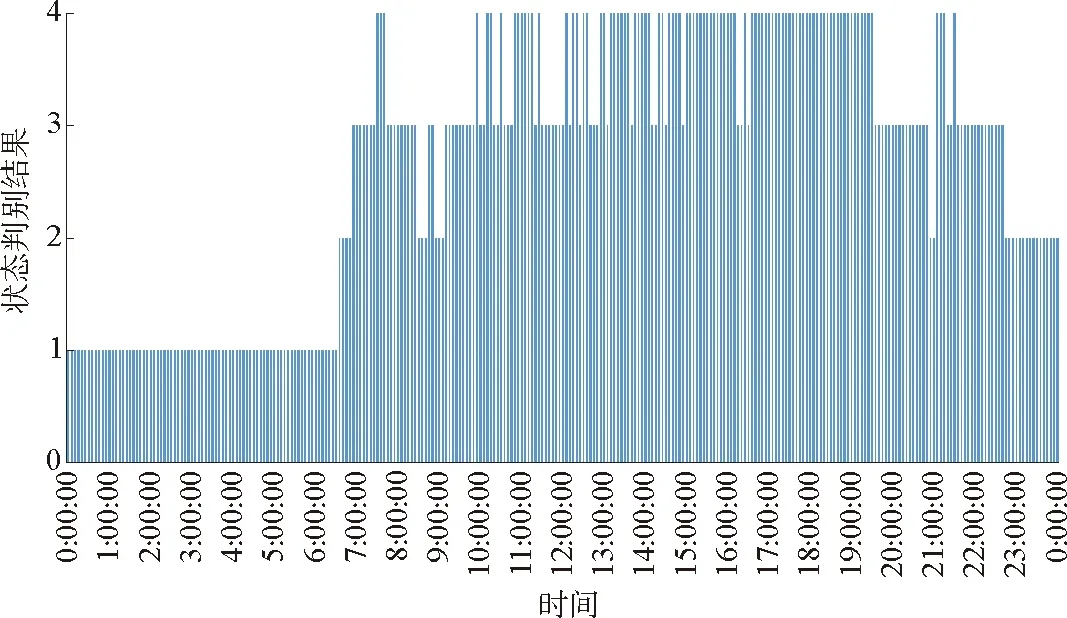
图1 截面S交通状态判别结果

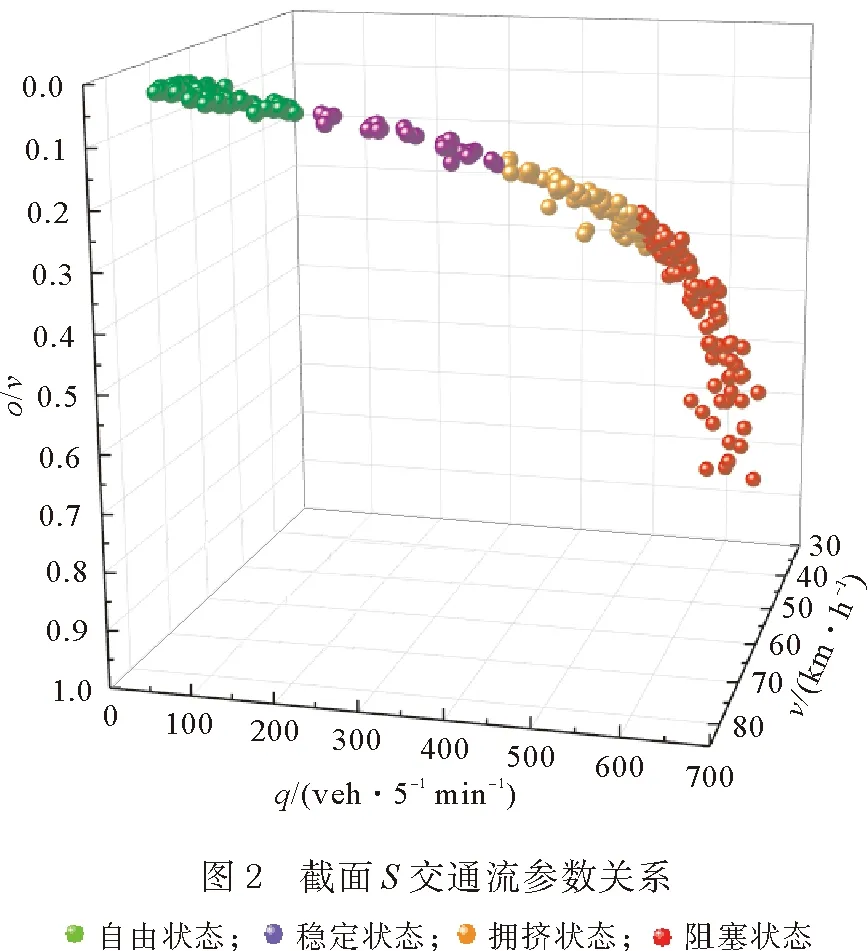
图1纵轴1—4分别代表自由流状态、稳定流状态、拥挤流状态、阻塞流状态，数据共有289组。其中自由流状态为94组，占比32.53%；稳定流状态为88组，占比30.45%；拥挤流状态为28组，占比9.69%；阻塞流状态为79组，占比27.34%。由图1、图2可知，该快速路道路状况基本畅通，大多数拥堵主要集中在早晚高峰，说明本文方法能有效地对交通运行状态进行分类，且与实际状况相符。

3.3 对比分析

本文以判别率和误判率为指标，根据上述获取的交通流数据，分别使用传统K-means算法和改进K-means算法对其进行交通状态判别，与道路实际运行状况相比，得到4种交通状态下的判别率和误判率，如表8所示。

从表8可以看出，在4种交通状态下，改进K-means算法判别率为97.21%，误判率为0.74%，其判别精度比传统K-means算法提高了8.13%，误判率降低了1.05%。由此可见，改进K-means算法可获得较好的判别效果，在交通状态判别上具有一定的优势。

表8 交通状态判别效果对比 %

4 结论

1) 传统交通状态判别指标的选取都是按照一定的标准和规定，进行直接选取，本文采用因子分析，从q，v，o，k，t，s，o/q，o/v8个交通流参数中，提取出q，v，o/v最为适合的3个交通状态判别指标。减少交通流参数的选取对算法应用效果的影响，更好地呈现交通状态变化规律。

2) 改进K-means聚类算法创新点在于建立了交通状态判别综合评价函数，将聚类数K和初始聚类中心同步进行优化。

3) 本文将因子分析与改进K-means聚类算法相结合在一起，通过实例验证，这种方法对快速路交通运行状态可以有效判别。