基于动力测试的高层建筑损伤定位研究

翁翔宇，刘才玮，苗吉军,*，张天亮，修 杨，徐玉野

(1.青岛理工大学 土木工程学院，青岛 266033; 2.华侨大学 土木工程学院, 厦门 361021)

本文以青岛市某拆迁安置房为研究对象，建筑尺寸为51 m×18.9 m×74.85 m(长×宽×高)，建筑面积为19 417.9 m2。其中地下负1层为停车场，地上24层为民用住宅。建筑结构形式为钢筋混凝土框架-剪力墙结构，其中底部4层为加强层。建筑结构类别为丙类，设计使用年限为50年，地区抗震设防烈度为7度，场地特征周期0.45 s，地震分组为第三组。建筑结构构件混凝土强度等级设计值见表1。

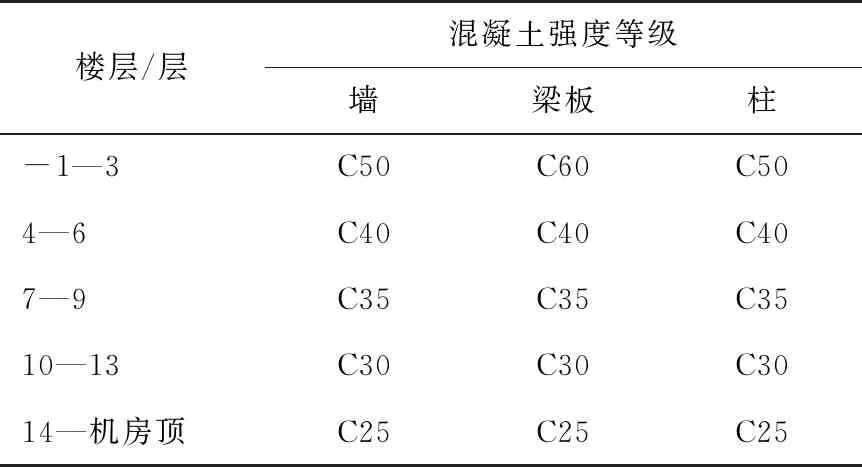
表1 混凝土构件设计强度等级

该高层框架-剪力墙结构主体结构基本完工，后因故停工2年，现需二次开工，为了确保工程安全性及结构可靠度，需重新对结构安全性进行检测。目前能够实现建筑结构安全性检测的方法主要包括常规检测及动力检测，常规检测识别精度较高，但工作量繁重，现场常规检测损伤楼层强度等级见表2，未标注构件混凝土强度等级与设计强度等级相同。

表2 混凝土实测强度等级

相对传统的常规检测，动力检测工作量少，但对于高层建筑结构缺少完善的理论支持及工程实例。狄生奎等[1]以悬臂梁结构为研究对象，设计不同的损伤工况，采用ζ参数法对结构进行损伤识别，识别结果较为理想;王高胜等[2]以输电塔架为研究对象，首先提出一种弯曲型集中质量模型的简化方法，针对损伤识别柔度法的病态性，提出损伤识别约束的柔度法，并分别从理论分析及数值算例验证了该方法的有效性；安永辉等[3]提出了比例柔度矩阵LU分解的结构损伤定位方法，并对某20层框架结构进行了数值模拟损伤定位研究，对一6层集中质量剪切框架模型进行了试验研究，损伤识别结果较为理想；彭念等[4]仅采用损伤后结构模态信息，提出相对损伤柔度曲率识别方法，对简支梁及连续梁进行了损伤识别研究；徐宏文等[5]基于模态曲率多项式曲线拟合的方法识别出平板损伤位置，但没有考虑噪声的影响；HSU等[6]通过模态曲率的损伤检测技术采用光栅应变传感器来获得模态曲率证明了该方法的可行性，但目前仍存在一定的局限性；付伟庆等[7]通过基于均匀设计试验的框架结构正分析分步式损伤识别的方法，对多层框架结构各层损伤状况识别较为精确，大幅减少了对神经网络多结构损伤状况的训练次数；RUFFELS等[8]通过马氏距离和K-S检验2种离群值检测方法对跨度5 m的钢拱桥的实验室模型进行了无模型损伤检测，成功检测到了损伤及损伤过程。以上方法大都针对于数值模拟或者试验模型进行的，对实际工程应用尚有距离。

基于此，本文以高层框架剪力墙结构为研究对象，首先进行数值仿真分析，研究不同损伤识别方法的可行性。基于分析结论，结合实测数据对高层框架剪力墙结构进行损伤识别，并与常规检测结果进行对比。

1 动力检测损伤识别方法可行性研究

1.1 数值仿真模型及损伤工况

本文采用SAP2000建立有限元模型，以设计信息为依据，考虑到实际建筑结构只完成了主体结构，并未做外墙抹灰及装饰，因此只需要考虑承重结构自重；为简化模型，不考虑部分构造对结构质量分配的影响；模型中，墙、板利用分层壳单元进行建模，其他构件按照常规进行建模。

参考常规静力检测结果，本文通过降低楼层梁、柱、墙、板混凝土强度等级的方式，设计了8种损伤工况，用以研究损伤识别方法的可行性。损伤工况设计见表3。其中损伤工况L1，L2，L3分别用于研究不同损伤位置处损伤识别效果；L3，L4用于对比研究单损伤情况下不同损伤程度识别效果；L5，L6用于对比研究多损伤情况下识别效果及损伤程度对损伤识别的影响；L7用于研究多损伤情况下损伤识别效果；L8用于研究对于紧邻损伤情况下的识别效果。

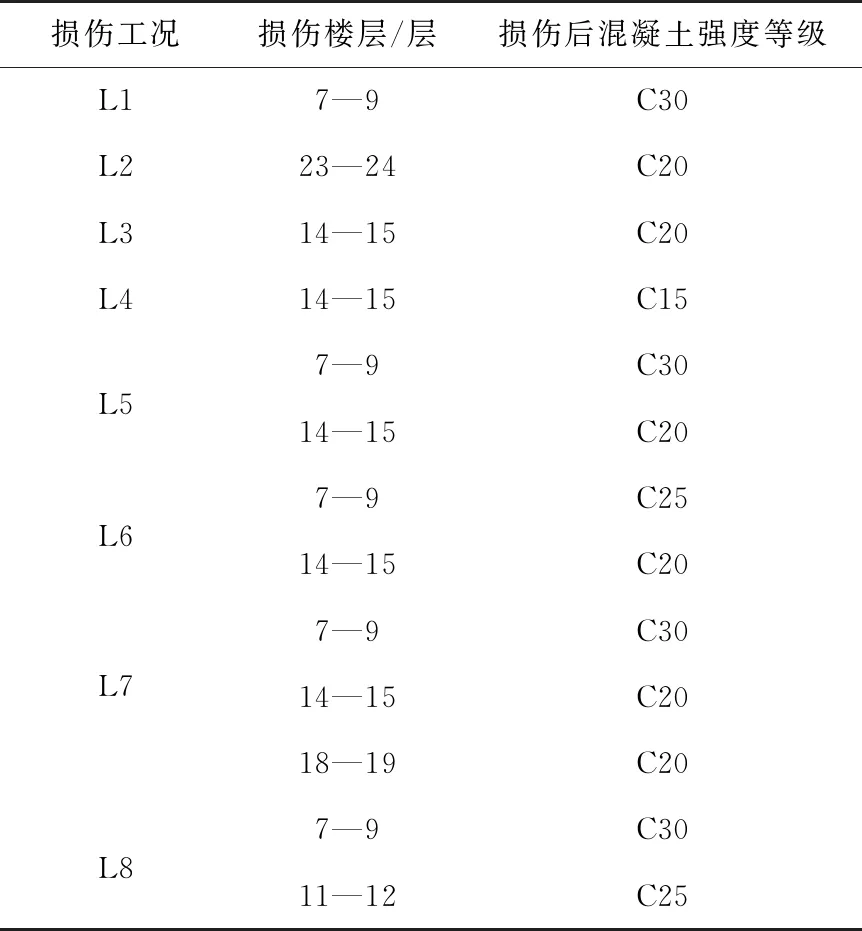
表3 模型损伤工况

1.2 基于曲率模态的损伤识别方法可行性研究及测点数量影响分析

曲率模态计算公式如式(1)(2)所示。

(1)

(2)

式中：ρ为曲率；M为弯矩；EI为抗弯刚度；ρij为第i阶j测点振型曲率；φij为第i阶j测点振型；hj为j层层高。

式(1)是曲率模态的识别原理公式，当结构受到损伤时，结构刚度或质量分布发生改变，结构曲率因此产生改变；式(2)是曲率模态实际计算公式。研究发现，基于振型曲率的损伤识别方法主要存在以下缺点[9]：①模态振型是相对值，不同的归一化方法对应的振型曲率计算结果不同；②在曲率零点位置往往存在较大的误差；③由式(2)可知，在振型曲率计算过程中，测点j的振型曲率不仅与j点的振型有关，还与测点j-1及测点j+1模态振型有关。刘义伦等[10]利用曲率振型规范化处理及零点特殊处理提出了问题①及问题②的解决方案，但问题③属于曲率模态理论计算不可避免的问题，因此基于曲率模态的损伤识别方法很难准确识别损伤位置。

为研究曲率模态损伤识别方法的可行性，本文分别拾取了各损伤工况下前6阶模态振型，分别研究曲率模态差及振型曲率模态相对变化率的识别效果，其中曲率模态差、曲率模态相对变化率计算公式分别如式(3)、式(4)所示：

Δρij=ρ′ij-ρij

(3)

(4)

式中：ρij，ρ′ij分别为损伤前、后i阶j测点振型曲率。

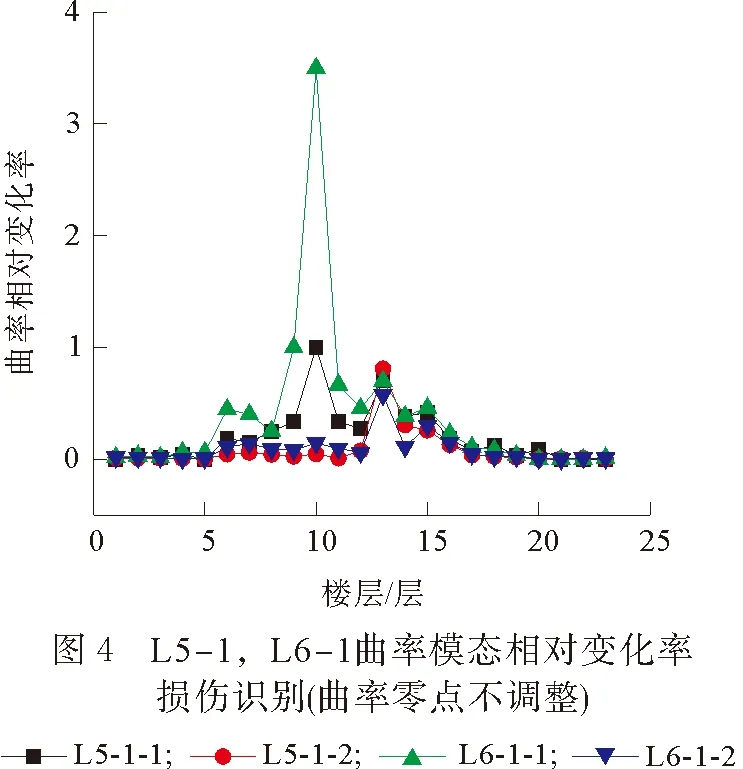
识别过程中涉及的振型归一化方法及曲率零点处理方式借鉴文献[10]进行处理。部分损伤识别效果如图1—5所示。图中L1-2-1表示1损伤工况2阶1方向识别情况。

限于篇幅，只列举部分识别结果，综合各工况识别效果分析如下：

1) 曲率模态差识别结果：

①损伤位置位于曲线突变处。曲线的突变性是相对于曲线的总体趋势而言的。当结构存在多处损伤或邻近损伤时，如图1所示，基于曲率模态差的损伤识别方法很难准确识别损伤位置，损伤识别范围大于实际损伤范围。

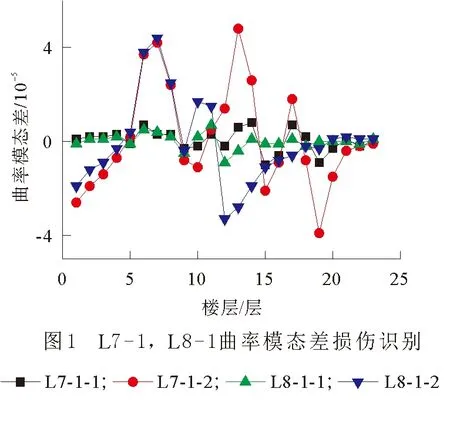
②同一阶次下，基于主振方向识别效果较次要方向识别更为理想；同一损伤工况下，综合2个方向，基于不同阶数的损伤识别结果较为接近，识别范围较为明确。

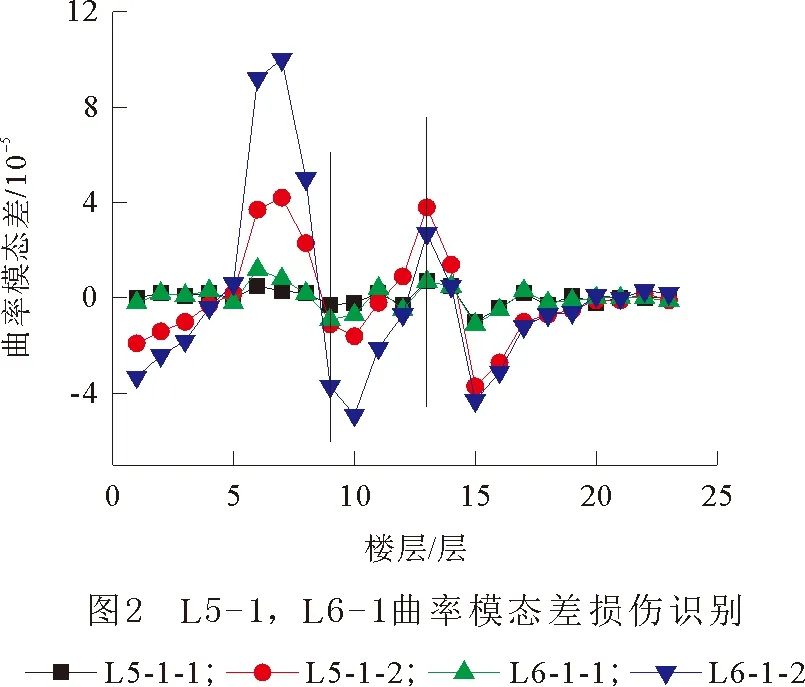
③由图2分析可知，在7—9层损伤位置，随着损伤程度的增加，曲率模态差变大；相比之下，14，15层损伤识别结果受7—9层损伤程度影响较小。

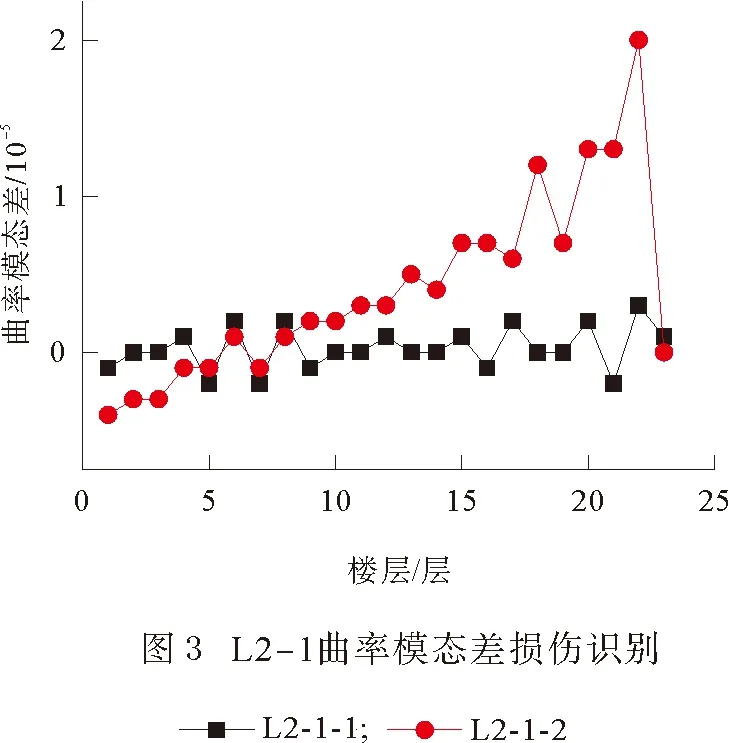
④由图3分析可知，基于曲率模态的损伤识别方法对于顶部损伤识别效果不甚理想。

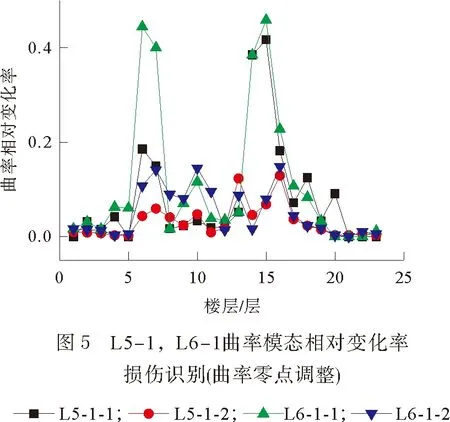
2) 曲率模态相对变化率识别结果。由图4、图5对比分析可知，曲率零点调整后，虽然改善了识别结果，但损伤位置识别存在错误定位现象，并且综合8种损伤工况，每种工况6阶的损伤结果，基于曲率相对变化率的损伤识别方法在损伤位置存在峰值，但识别效果较为凌乱，不同阶数的识别结果并不一致，存在较大的差异性。相比之下，基于曲率模态差的损伤识别方法更具有实际应用意义。

在进行高层建筑结构动力测试时，受测点数量及传输线长度限制，可能无法实测每层结构模态信息，下文以损伤工况1为研究对象，选取1阶主振方向振型计算曲率模态差用以研究测点较少的情况下曲率模态差损伤识别效果，如图6所示。分析可知：

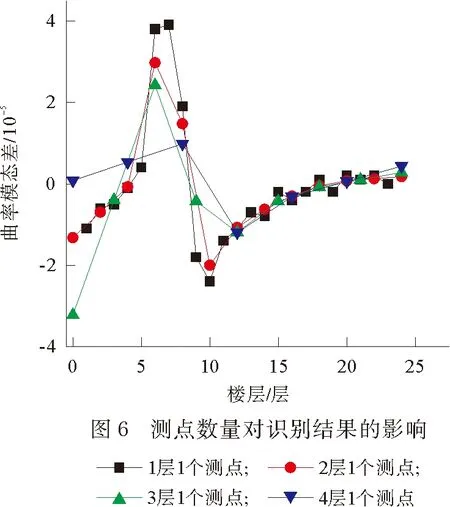
①基于文献[10]提出的两端曲率近似计算方法，当测点较多时，能够满足精度要求；但当测点较少时，则无法正确表述端部位置曲率模态值。

②当测点较少时，尤其当测点跨过损伤位置时，如4层1个测点时，基于曲率模态的损伤识别方法已不具有识别效果。从图6分析可得，2层1个测点的曲率模态差识别结果基本能够反应损伤大致位置。

1.3 基于柔度矩阵的损伤识别方法可行性研究及测点数量影响分析

柔度矩阵(F)计算公式如下：

(5)

式中：φi为第i阶质量归一化振型；wi为第i阶固有频率。

柔度矩阵损伤识别方法优点在于物理意义明确，并且只需前几阶振型就能够达到足够的精度，但是柔度矩阵计算值Fij不仅与i位置损伤有关，还受其他位置损伤影响。在柔度矩阵损伤识别方法研究过程中，为提高识别精度及灵敏度，相继衍生出模态柔度差、模态柔度改变率、模态柔度差曲率、模态柔度改变率曲率及灵敏度分析等识别方法。对于柔度曲率系列损伤识别方法，限于曲率方法无法准确识别损伤位置的本质缺陷，本文不对其进行研究。

对模态柔度差及模态柔度改变率[11]对比识别进行研究，模态柔度差(ΔF)及柔度改变率(δF)计算公式分别如式(6)、式(7)所示。损伤工况6识别矩阵及对角线识别效果如图7—10所示。

ΔF=Fd-Fu

(6)

(7)

式中：Fd为损伤后的柔度矩阵；Fu为损伤前的柔度矩阵。

由图7、图8可以看出，三维识别效果图在损伤位置处斜率发生改变，其中基于矩阵对角线识别效果较为明显。图9、图10是基于矩阵对角线进行识别的结果，由识别结果分析显示，曲线在损伤位置处斜率发生改变，且基于柔度改变率的识别效果较柔度差识别效果更加明显。针对不同损伤程度对比显示，损伤越严重，曲线斜率变化越大。但综合三维识别效果及对角线识别效果，基于柔度差或柔度改变率的损伤识别方法，对于高层框架剪力墙结构损伤识别并不明显。

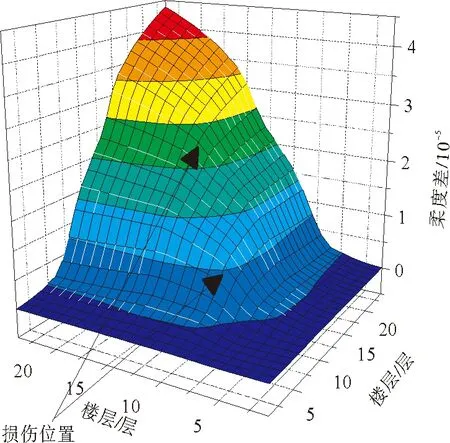
图7 L6柔度差识别距阵

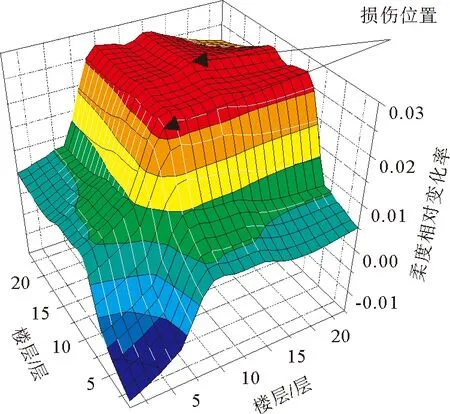
图8 L6柔度改变率识别距阵

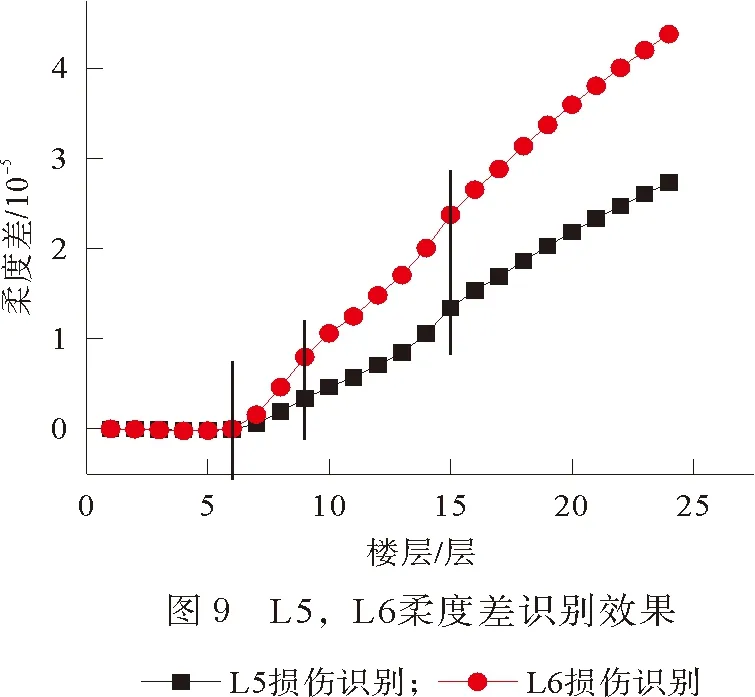
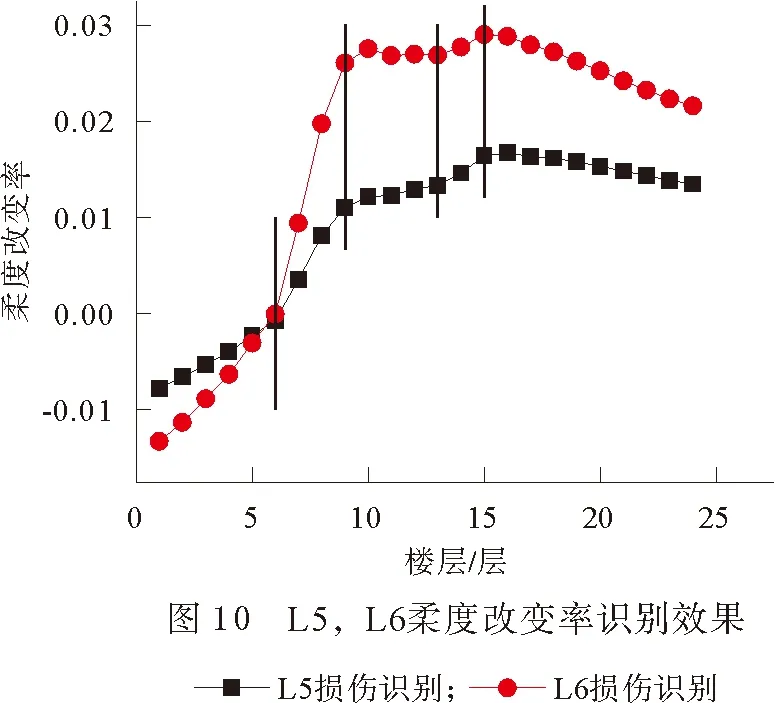
柔度矩阵改变率灵敏度分析[11]计算公式如下：

ξi+1=|(δFi+1-δFi)/ΔL|

(8)

式中：δFi为柔度改变率矩阵最后一列元素。ΔL为单元长度差。

在研究过程中发现，基于柔度矩阵改变率灵敏度分析的识别方法对于损伤位置存在虚假点，据此本文提出基于柔度矩阵差灵敏度分析的损伤识别方法，计算公式如下：

ζi+1=|(ΔFi+1-ΔFi)/ΔL|

(9)

式中：ΔFi为柔度差矩阵最后一列元素；ΔL为单元长度差。

柔度差及柔度改变率灵敏度分析识别效果如图11、图12所示，分析可知：

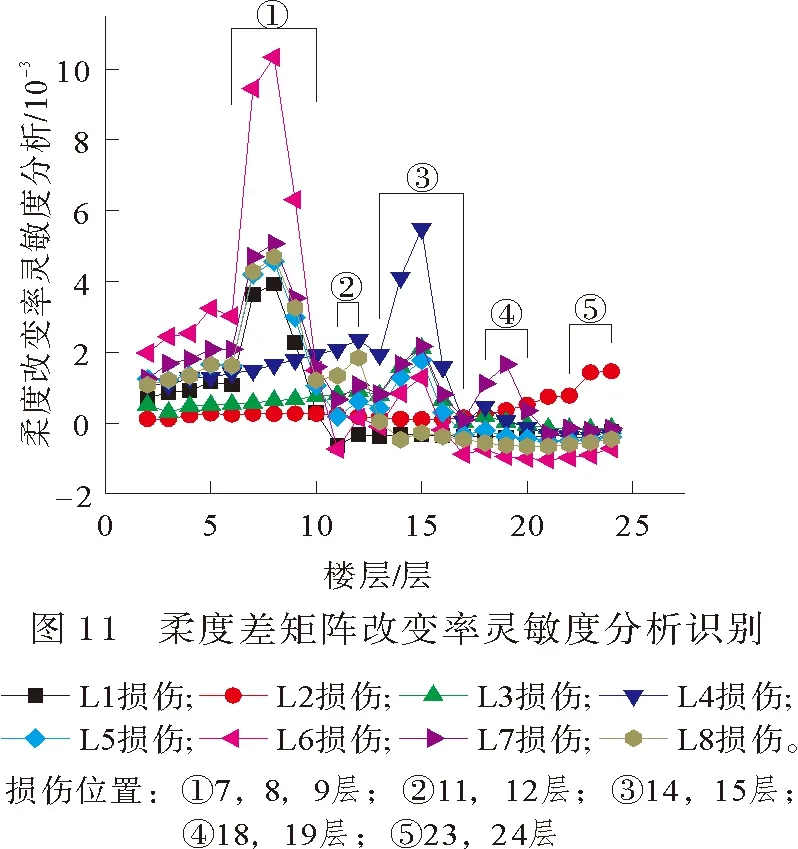
1) 由图11分析可得，损伤位置位于曲线峰值处，但由于峰值覆盖范围不定，准确识别范围无法确定；由损伤工况L5，L6，L7对比分析显示，多处损伤时，损伤越严重，灵敏度值越大，且相同损伤程度楼层，损伤程度识别不受其他楼层损伤程度影响。对于邻近损伤，识别范围较为模糊。

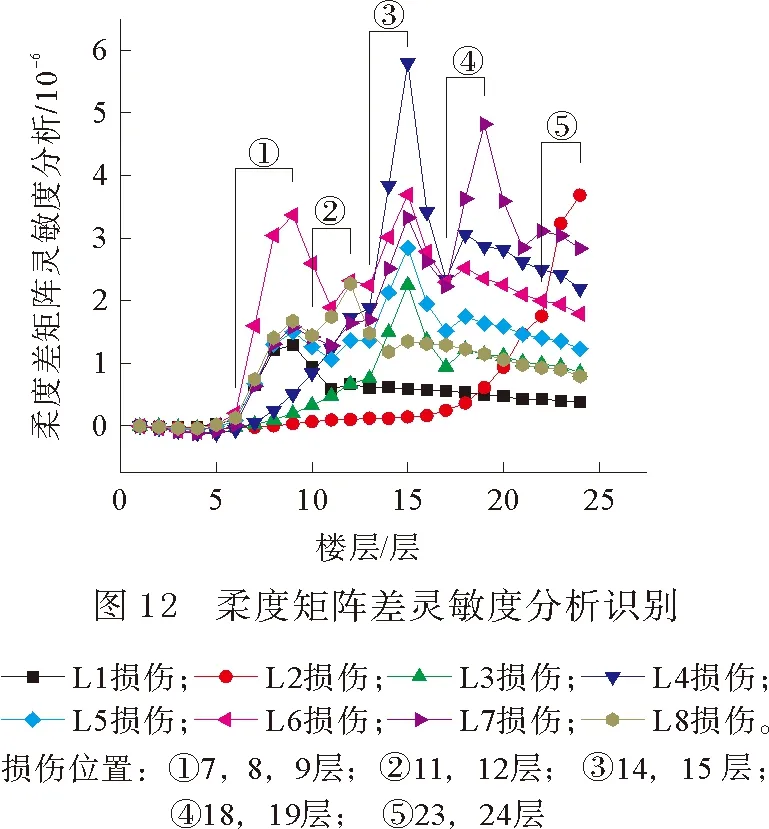
2) 图12损伤识别结果显示，损伤位置位于曲线波动处，损伤从第1个斜率突增点开始至峰值为损伤位置，损伤位置识别准确；多处损伤时，损伤越严重，灵敏度值越大，但受其他楼层损伤影响，相同损伤程度楼层损伤识别略有不同，且无损伤顶层灵敏度分析值ζn受其他损伤影响，并不为零。以下介绍测点数量对灵敏度分析方法的影响。

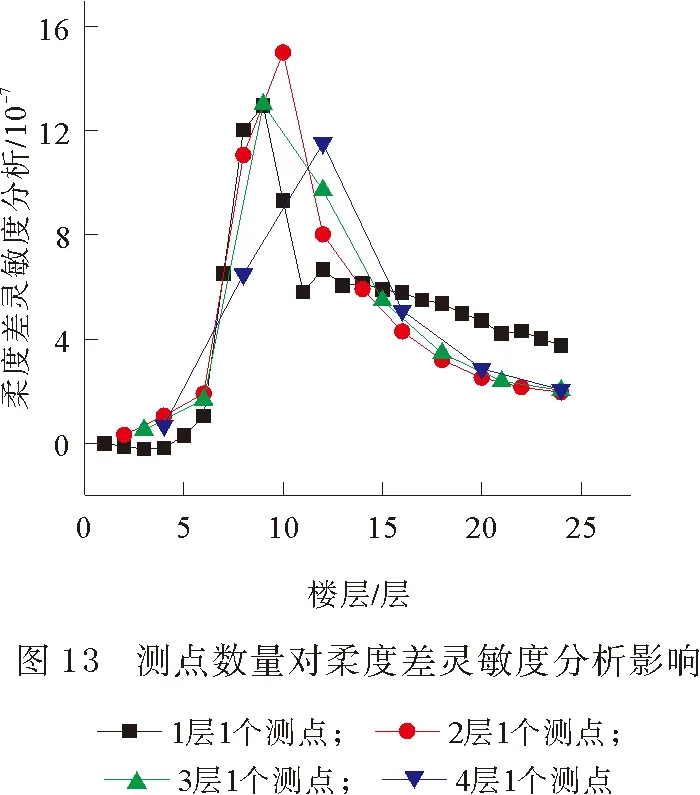
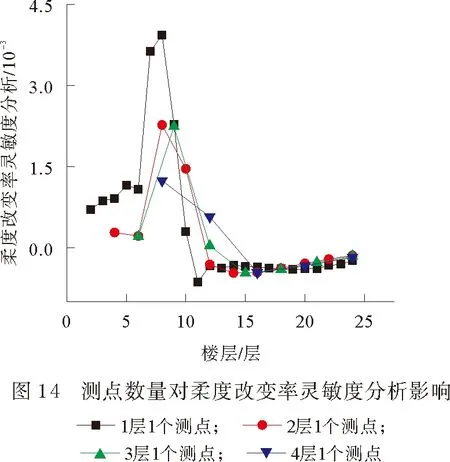
图13、图14为损伤工况L1改变测点数量后的识别效果，分析可知，改变测点数量后，虽然最小识别范围变大，但识别范围包含损伤范围，识别结果较为精确。对比显示，基于柔度差灵敏度识别方法较柔度改变率灵敏度识别方法识别更准确，且能对底部第一节点计算进行相应处理。

综合柔度差灵敏度及柔度改变率灵敏度分析识别结果，本文提出综合灵敏度识别方法，即同时采用2种方法进行识别。改进后的方法既能够准确识别损伤位置，又能够确保同一位置相同损伤程度幅值不受其他损伤影响，并且具有无损伤位置识别结果趋近于零的特性。

2 结构动力测试及损伤分析

基于对曲率模态损伤识别方法及柔度矩阵系列识别方法的可行性研究[12]，本文提出综合灵敏度损伤识别方法。现场振动测试采用环境激励方法，结构测试系统采用TST-5912动态信号测试分析系统，测量传感器采用磁电式速度传感器，测量频率范围为0.25～100 Hz。

基于现场实测模态信息，利用TST模态分析软件拾取结构模态信息，并基于GAO等[13]提出的损伤前后归一化振型向量长度不变的假定，对模态振型进行质量归一化处理，即

φuj,pTφuj,p=φdj,pTφdj,p

(10)

(11)

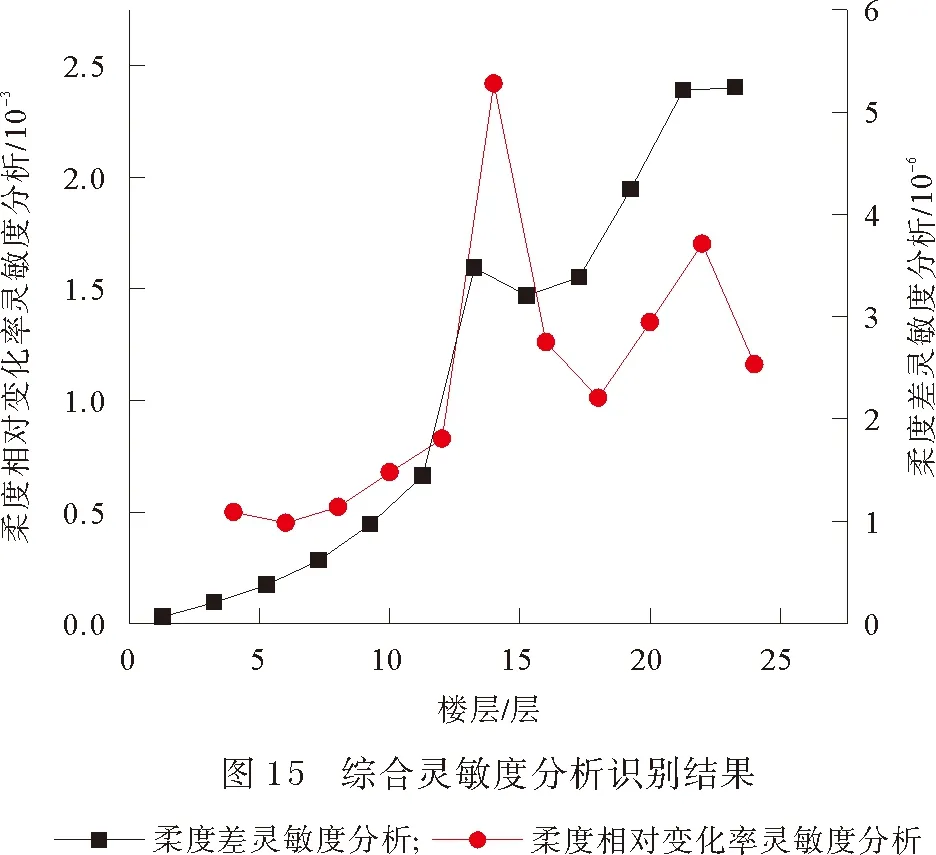
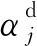
基于质量归一化模态振型损伤识别结果如图15所示。由图15可以看出，结构在13，14层及19—24层存在损伤，与常规检测结果对比显示，本文提出的综合灵敏度损伤识别方法能够定位损伤位置，但受最小识别范围限制，基于动力检测识别的损伤范围大于常规检测。此外需要特别说明的是，虽然损伤程度仍需由常规检测方法确定，但动力测试方法可大大减少常规检测的样本数量，具有一定的工程应用价值。

3 结论

1) 基于曲率模态的损伤识别方法能够粗略识别结构损伤，但由于方法的固有缺陷，无法准确识别损伤位置。

2) 基于柔度矩阵进行的损伤识别方法，物理意义明确。其中柔度差及柔度改变率损伤识别方法对于高层框架结构损伤识别并不理想；柔度改变率灵敏度分析方法难以准确识别损伤位置，并且对于起点计算方法存在缺陷，而本文提出的柔度差灵敏度识别方法能够准确识别损伤位置，且计算完整。

3) 对于高层框架剪力墙结构，综合灵敏度损伤识别方法能够识别损伤位置，虽然损伤程度仍需常规检测方法确定，但其大大减少了常规检测的工作量，具有一定的工程应用价值。