SPH方法与经典边坡稳定分析方法的对比研究
翟 明,李 亮,*,王上上,刘 旭,陈 富,杨正权
(1.青岛理工大学 土木工程学院,青岛 266033;2.中国水利水电科学研究院,北京 100048)
在众多岩土问题中,边坡失稳事故尤为突出。作为岩土工程三大经典问题之一,边坡稳定问题引起了国内外学者的广泛关注。目前常用的边坡稳定分析方法主要有三种,即极限平衡法(Limit Equilibrium Method, LEM)、强度折减法(Strength Reduction Method, SRM)和极限分析上限法(Upper Bound Limit Analysis Method)。极限平衡法[1-2]是最早用于边坡稳定分析的方法,目前已趋于完善和成熟。极限平衡法主要包括两个步骤:①计算给定滑动面的安全系数;②基于智能优化算法变换不同的滑动面并计算其安全系数,确定最小安全系数及其对应的临界滑动面。强度折减法思想最早由ZIENKIEWICZ等[3]提出,后来被许多学者广泛应用于边坡稳定分析。强度折减法的基本思想是将土体初始抗剪强度参数(黏聚力c、内摩擦角φ)不断进行折减,直至边坡达到临界状态,此时的折减系数即为安全系数。极限分析上限法[4]的基本思想为:对于给定的失效模式,从变形协调出发,根据外力功和内能消散相平衡的原理确定相应的安全系数,然后应用最优化方法,确定相应于最小安全系数的临界失效模式。上述三种方法在边坡稳定分析中均有应用,对于复杂荷载工况、复杂边坡剖面的边坡而言,如何检验三种方法的适用性并比较其计算性能对于边坡稳定分析具有较强的指导意义。
近年来,光滑粒子流体动力学(Smoothed Particle Hydrodynamics,SPH)方法[5-9]逐渐被用于岩土工程领域,BUI等[5]较早地将Druck-Prager本构模型引入SPH方法中,进行了一系列岩土工程问题的模拟,为SPH方法在岩土工程问题中的应用奠定基础。黄雨等[6]采用Bingham流体模型描述土体的流动大变形,并进行了SPH数值模拟,结果与模型试验实测数据基本吻合,表明SPH方法对于土体大变形分析的有效性。唐宇峰等[7]研究了SPH在边坡稳定计算中的失稳判据,LI等[8]用SPH方法并结合极限平衡方法的安全系数模拟了边坡临界状态时的位移云图,在此基础上评估了极限平衡方法的临界滑动面。由此可见,SPH方法能够模拟滑坡从发生、运动直至最终土体堆积的整个过程,其位移场云图可以结合强度折减法塑性剪应变增量云图,从而全面直观地比较传统分析方法的临界滑动面。在简要叙述边坡稳定分析方法的基础上,采用三个边坡算例,分别比较了三种边坡稳定分析方法的结果,得出了有意义的结论。
1 方法介绍
1.1 极限平衡法
极限平衡法(LEM)是最早应用于边坡稳定性分析的方法。极限平衡法大多以垂直条分法为基础,通过引入条间力函数假定使问题变得静定可解,从而利用力和力矩平衡方程得出边坡稳定安全系数。目前已有多种基于极限平衡理论的边坡稳定分析方法,如瑞典法、Bishop法、Janbu法、Spencer法、Morgenstern-Price法等。由于传统的极限平衡法计算简便、概念清晰,现在仍然是工程师所采用的主要方法。本文极限平衡法采用的计算程序为GEOStudio中的SLOPE/W,计算方法选取常用的Spencer法。
1.2 强度折减法
(1)
式中:c,φ为土体的初始黏聚力和内摩擦角;c′,φ′为折减后土体的黏聚力和内摩擦角;F为折减系数。
本文采用强度折减法结合有限差分的数值计算程序FLAC软件求解边坡稳定安全系数,采用塑性剪应变增量云图来查看滑动区域。
1.3 极限分析上限法
极限分析上限法有很多实现途径,本文采用最新提出的不连续布局优化[10-11]方法(Discontinuity Layout Optimization,DLO)。不连续布局优化使用严格的线性优化技术识别分布在土体中节点之间的不连续discontinuity的关键布局,它可以识别块体的滑动和平移,能够利用数学优化技术识别关键的破坏滑移线。
DLO方法以节点来离散求解域,节点之间相互连接,形成多个不连续discontinuities(以下简称disc),然后将土体参数赋予每个不连续disc,在荷载作用下,位移增大,外力做功也相应增大,当外力做功与系统的能量耗散相等时,达到极限状态。采用数学优化技术规划多条可能的路径,对路径中每一个不连续disc进行搜索,计算路径的能量耗散,能量耗散最小的路径即为破坏路径。DLO方法确定破坏模式的过程如图1所示,首先描述所要求解的问题(图1(a)),然后以一定密度的节点离散所求解问题的几何体(图1(b)),节点之间相互连接形成不连续disc(图1(c)),最后应用有效的数学优化技术得到破坏时的滑动面(图1(d))。需要注意的是,DLO的计算过程中,所布设的节点、方式、密度、本构模型参数取值以及边界条件的设定对结果都会有影响,本文所采用的计算程序为LimitState:GEO,采用其默认设置,网格密度取中等。
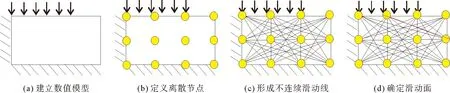
图1 DLO方法确定破坏模式的过程
1.4 光滑粒子流体动力学方法(SPH)
SPH[5-9]是一种无网格的数值方法,与有限元等需要划分网格的数值方法不同,SPH方法用有限个粒子来离散问题域,不需要网格划分和小变形假设,这使得SPH可以不受网格畸变问题的影响,因此,SPH方法可以直接用于模拟岩土工程的大变形问题。SPH的概念图如图2所示,每个粒子被赋予状态变量(含有速度、位移、应力、应变等)和材料属性(含有重度、黏聚力、内摩擦角、弹性模量、泊松比等)。
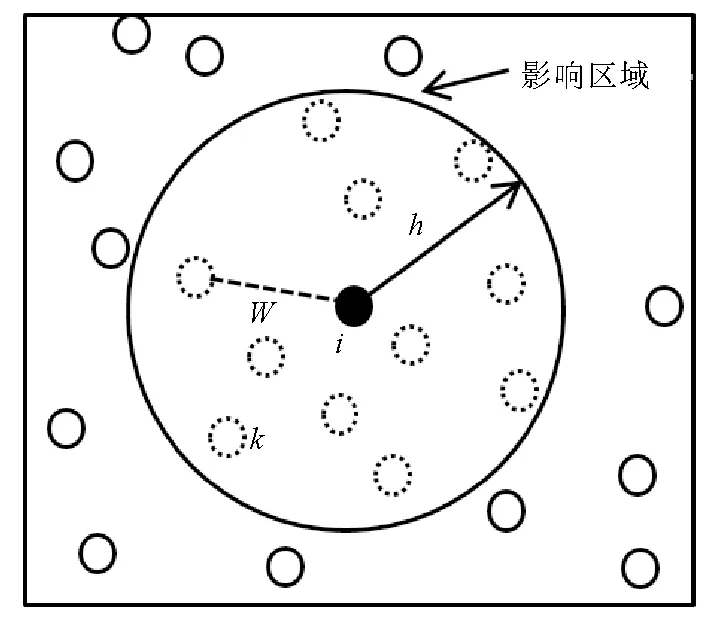
图2 SPH的概念
图2中黑色实心圆圈所示的粒子i的信息通过核函数W与影响区域内临近粒子k相互作用来获得,与影响区域外的粒子无关,影响区域通过变量h来确定。SPH方法中粒子的运动信息由质量守恒方程(式(2))和动量守恒方程(式(3))确定。
(2)
(3)
式中:N为粒子总数;ρ为粒子中土体的密度;m为粒子质量;v为粒子的速度;t为时间;Wik为粒子i与粒子k间的光滑核函数;σ为单个粒子的总应力张量,其表达式由土体的本构模型确定;x为粒子位置;α,β为不同的坐标轴;fα为外力引起的加速度分量。
根据式(1)~(7)可得:第10个考核期Cpv为3.976万元,Cav为4.704万元,Ev为3.96万元,Vs为-0.016万元,Vc为-0.744万元,Is为1.034,Ic为0.842。由计算结果可知:该项目在第10个考核期实际安全成本投入处于超支状态,实际安全保障水却没有达到计划水平,可以排除是由于安全成本节约导致了安全度的降低,很明显是由于管理措施不到位而造成的,项目经理部应结合专家对当月安全评价体系的评分情况和项目实际安全投入情况进行深入分析,找出原因,加强安全管理力度的同时严格控制安全成本的支出,保证项目施工安全顺利开展。
SPH方法模拟岩土工程问题时,算法参数取值对计算结果有重要影响。譬如,核函数W,影响半径h以及边界问题处理时所需的人工黏性比例因子等。本团队基于SPH方法的基本原理与公式自编了Fortran程序,并进行了3年的调试,与前人的研究结果进行了对比,并发表了相关文章,可参阅文献[8]。
2 SPH验证
应用本团队自编SPH程序来模拟砂柱垮塌试验,模拟结果与HUNGR[12]所做的模型试验结果进行对比,来验证自编SPH程序的可靠性。砂柱高度为0.2 m,宽度为0.4 m,密度ρ=1630 kg/m3,黏聚力c=0 kPa,内摩擦角φ=30.9°。在SPH参数设置中,两个主要的参数为粒子的间距与影响半径h,MAO等在文献[9]中对SPH方法的参数做了细致的研究,本文参数取值参考文献[9]研究结果进行。将粒子半径取为0.005 m,影响半径取为0.006 m,共产生3200个粒子,分析模型如图3所示。

图3 砂柱试验SPH分析模型
SPH方法的计算过程包含两个步骤,首先模拟荷载作用下土的固结过程,固结完成以后,再模拟土体在荷载作用下的失稳滑动过程。SPH方法模拟砂柱垮塌后的形态与文献[12]的试验结果对比如图4所示。
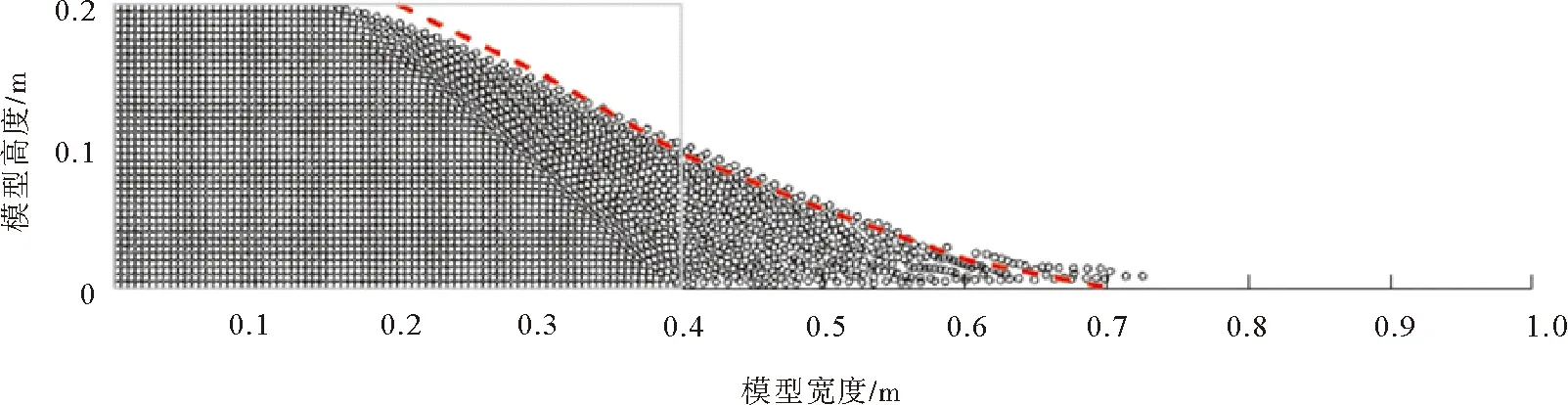
图4 砂柱试验的SPH模拟与试验对比
图4中,红色线为砂柱垮塌试验完成后的坡面曲线。由图4可知,SPH方法模拟的结果与实验室砂柱垮塌试验结果表现出了良好的一致性,所以,本团队自编SPH程序可以用于模拟滑坡过程中的大变形问题,其位移场云图可以与强度折减法塑性剪应变增量云图一起来综合衡量边坡稳定性问题。
3 算例分析
3.1 算例1
考虑图5所示的简单均质边坡,模型宽度为20 m,总高度为10 m,其中坡高为6 m,坡角45°。假设土体材料服从Mohr-Coulomb强度准则,黏聚力c=20 kPa,内摩擦角φ=17°,重度γ=19 kN/m3。

图5 算例1模型
对于算例1,分别使用极限平衡法、强度折减法、不连续布局优化法进行分析,得到的安全系数分别为1.623,1.674和1.742。其临界滑动面和塑性贯通区如图6所示。

图6 算例1临界滑动面及塑性剪应变增量云图
通过图6中三种方法结果的对比可知,极限平衡法和强度折减法所得安全系数基本一致,DLO所得安全系数略高;极限平衡法和不连续布局优化法得到的临界滑动面非常接近,均落在强度折减法的塑性破坏区内(由塑性剪应变增量云图确定)。所以,对于简单的均质边坡,三种方法所得临界滑动面几乎一致,安全系数略有差别。
应用SPH方法分析该问题,将粒子半径定义为0.1 m,影响半径取为0.12 m共产生3965个粒子,SPH分析模型如图7所示。利用原始参数进行边坡自重应力的模拟,进而将原始参数仿照强度折减法公式(1)进行折减,折减系数取为LEM所得安全系数,即F=1.623,将折减后的参数输入SPH程序,得到计算稳定时刻的位移场云图与LEM,DLO方法的临界滑动面比较如图8所示。
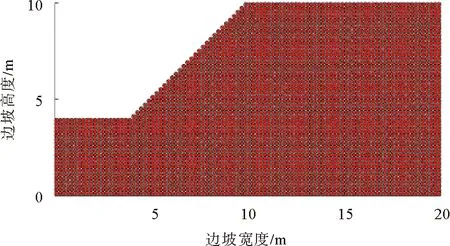
图7 算例1的SPH分析模型
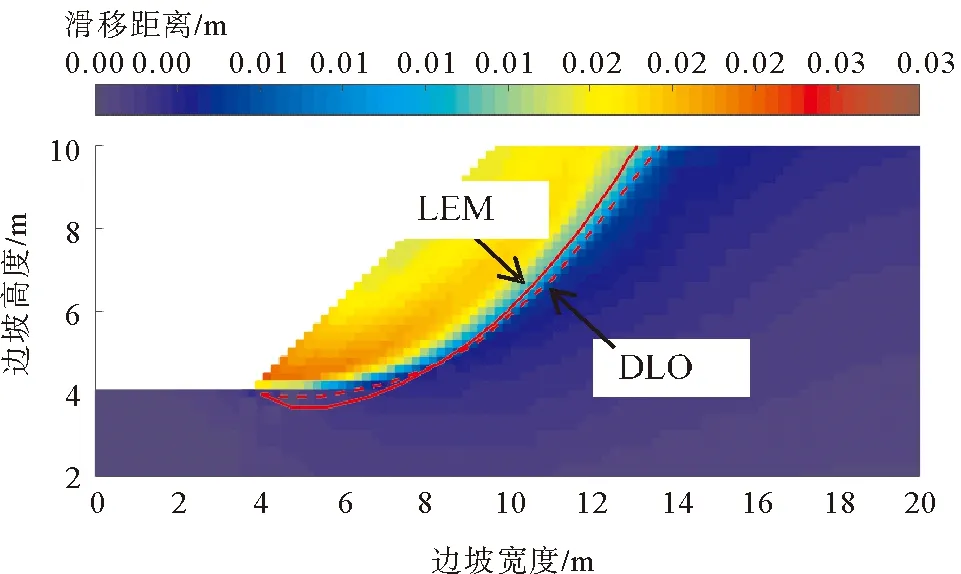
图8 算例1的临界滑动面及SPH位移场云图
由图8可以看出,SPH得到的位移场云图明显分为蓝色的不动区与青色/黄色以及红色所示的滑动区,二者之间的分界线与LEM,DLO所得临界滑动面基本吻合,从而间接验证了强度折减法所得塑性剪应变增量云图与SPH位移场云图在识别边坡滑动面方面的一致性。
3.2 算例2
边坡的几何尺寸与算例1保持一致,将土体黏聚力改为c=0 kPa,此时问题成为无黏性土坡的稳定性问题,此时的安全系数应为
(4)
式中:φ为土体的内摩擦角;β为边坡坡角。
极限平衡法得到的安全系数为F=0.33,破坏模式为表层破坏,与理论分析的结果一致。用强度折减法计算得到的安全系数为Fs=0.30,塑性剪应变增量云图如图9所示,同样为表层破坏模式。

图9 算例2的SRM塑性区云图
SPH方法得到的位移场云图如图10所示,同样为沿表层的滑移破坏。
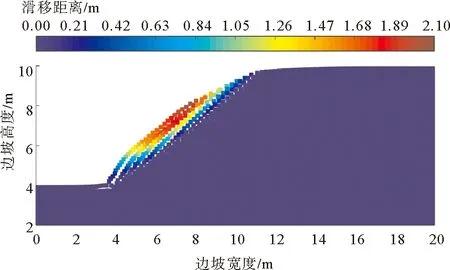
图10 算例2的SPH方法滑动位移
所以,极限平衡法、强度折减法以及SPH方法适用于无黏性土边坡的稳定性分析。而应用DLO方法计算该问题时,折减强度后输出的结果为“unknown”,折减荷载后的结果为“unstable”,均没能给出一个确定的安全系数。将黏聚力调整为c=1 kPa时,结果仍然不能确定。这说明DLO方法不能很好地处理c接近于0的几乎无黏性、纯摩擦情况的边坡稳定问题。在实际工程中遇到此类情况时应慎用DLO。
3.3 算例3
采用文献[11]中的算例,算例几何模型如图11所示,材料参数见表1。高度为8 m的大坝(土层A)修建于成层土地基上,其中第一层土为强度较高的砂土层(土层B),第二层为软弱层(土层C),最下层为基岩。

图11 算例3的模型

表1 算例3土层参数
分别应用LEM,SRM,DLO三种方法分析该问题,得到的临界滑动面、安全系数和塑性剪应变增量云图如图12所示。需要指出的是:由于该边坡为失稳状态,在SPH分析时,需要人为提高土层的强度参数以便获取边坡的自重应力,然后再利用原始参数进行滑坡过程的模拟。
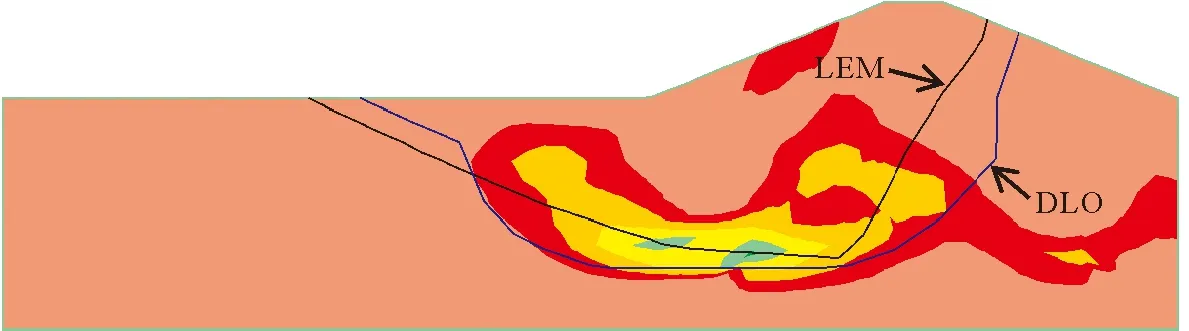
图12 算例3的LEM,DLO临界滑动面及SRM塑性区云图
由图12可知,LEM,SRM和DLO得到的安全系数分别为0.875,0.86和1.106,LEM和SRM所得安全系数基本一致。DLO方法的安全系数与LEM比较,计算误差为26.4%;与SRM比较,计算误差为28.6%,误差过大。
再分析该问题的临界滑动面,DLO方法得到的滑动面在土层交界处均出现一个比较大的凸(凹)角,这与SPH位移场云图吻合较好,而LEM的临界滑动面左右两部分的趋势变化不太明显,这种较为常规的滑动面在软弱交替土层中出现似乎是不合理的。另外,滑动面在软弱带中的部分,LEM的滑动面没有穿过软弱带到达基岩上部,而DLO方法的滑动面以及SRM,SPH方法的塑性区均到达基岩表面(图12、图13),这说明LEM寻找复杂边坡问题临界滑动面的能力有待提高。这是因为LEM通常需要人为设置滑动面形状和滑入、滑出范围,对于这种复杂的情况,潜在的滑入、滑出范围不明显,人为设置过于主观,存在一定误差。所以,对于确定复杂条件下边坡失稳的临界滑动面位置,DLO与SPH方法比LEM更加具有优势。

图13 算例3的LEM,DLO临界滑动面及SPH塑性区云图
对于几何模型复杂、存在软弱夹层等复杂地质条件的边坡稳定性问题,建议应用多种理论或软件进行分析,综合考量以得出正确的结论来指导工程设计。
4 结论
1) 对于简单的均质边坡,LEM,SRM和DLO方法均能得到令人满意的结果,可以得出合理的安全系数以及临界滑动面,SPH模拟得到的位移场云图与强度折减法所得塑性剪应变增量云图在识别临界滑动面方面具有一致性。
2) DLO方法对于接近无黏性、纯摩擦土体的情况会出现不易收敛,甚至计算失败的现象,遇到此类情况应慎用DLO方法。
3) 对于几何模型复杂、存在软弱夹层等复杂地质条件的边坡稳定性问题,在计算安全系数上,LEM与SRM所得安全系数基本一致,DLO方法所得安全系数偏高,误差较大。在确定临界滑动面上,DLO方法的结果与SPH方法的位移场云图十分一致,这是因为两者均不需对滑动面的位置做过多假设,对于确定复杂边坡的临界滑动面表现出了明显的优势。所以,对于复杂条件的边坡稳定问题,建议应用多种理论进行分析,综合考量后得出合理结论。

