基于驾驶人反应特性的车辆跟驰行为及模型

洪家乐，曲大义，贾彦峰，王 韬，黑凯先

(青岛理工大学 机械与汽车工程学院，青岛 266525)

随着城市交通拥堵问题的日趋严重，从交通流运行规律探索交通拥堵产生的根源已成为国内外学者关注的重点。而对车流运行动态特性的研究，国内外集中对道路运行车辆之间的跟驰现象进行了深度的分析。为了揭示跟驰过程中交通拥堵的产生条件与作用机理，国内外学者根据车辆相互作用关系建立了各类交通流跟驰模型，包括刺激-反应类、安全距离类、生理-心理类模型等[1]。这些模型描述了车辆跟驰过程中的相互关系，对道路交通流的研究起到了促进的作用，为交通拥堵的机理解析和稳定性调控提供了方法。

车辆跟驰模型[2]从动力学角度分析了同车道上前导车与跟驰车之间纵向速度与距离的关系，车辆是否安全跟驰行驶取决于以下几个因素：两车间距、速度、后车的期望速度以及交通流状态等。BANDO等[3]对Newell模型的加速度进行改进，提出的优化速度模型能够更好地拟合交通流运行。JIANG等[4]通过实测数据分析发现广义力模型存在车头间距小于安全间距且后车速度大于前车容易发生追尾的问题，提出了全速度差模型。随着对交通流模型研究的深入，学者们考虑到复杂道路中驾驶员特性与道路环境的影响，又对优化速度模型进行了改进，YU等[5]考虑相邻车辆加速度差的影响，改进了全速度差模型，降低了车辆在跟驰运行时的波动性。针对国内特有的一些交通流现象，喻丹等[6]考虑将期望车头时距视为常量，提出动态期望车头时距的跟驰模型，使得车辆跟驰可以表述车辆性能和驾驶员等差异引起的动态变化。曲大义等[7]考虑车辆跟驰受前导车和道路环境的影响，引入分子相互作用势建立改进跟驰模型，使得模型对实际交通流的拟合程度更高。安树科等[8]考虑将多前车速度差及车间距等信息反馈改进跟驰模型，研究了多前车优化速度在扰动过程中起到的作用，拓展车辆跟驰的维度，使得车流跟驰运行更为平稳。因而研究车辆跟驰有必要探讨跟驰车辆对于车头间距的变化所产生的影响，故本文引入驾驶员在不同车头间距条件下的反应特性，基于车头间距反馈构建了考虑驾驶员特性的改进车辆跟驰模型，采用数值仿真方法验证了驾驶员在跟驰中对于车间距的反应强度的影响。

1 驾驶员反应特性分析

驾驶员反应特性是驾驶员在跟驰过程中由于外界车辆刺激进行反应操作的特性，即跟驰车受前车速度、车间距影响呈现的制约性，对前车行进状态反应呈现的延迟性，由制约性和延迟性导致车间状态呈现的传递性。车辆跟驰的前提是：①道路平直，无交叉口和匝道，不允许超车；②车流是非自由流；③后方车辆的运行情况受前车的运行状态影响。假设本车为跟驰车时，在跟驰行驶的情况下，跟驰驾驶员通过观测与前车的间距进行反应操纵，有两种跟驰情况：

1) 前后车间距较大时，前车运行状态对后车的制约变小，后车可能会加速或匀速行驶，达到一定程度后前车的运行状态对后车的制约又变大的跟驰模型；

2) 前后车间距较小时，前车对后车的影响较大，后车可能匀速或者减速行驶，经过一段时间后发现前车影响变小时又重新恢复原本运行状态的跟驰模型。

这些由于驾驶员反应引起的跟驰现象对于交通流运行状态有着重要影响。

2 跟驰模型构建

传统的车辆跟驰模型可以简单表示为

(1)

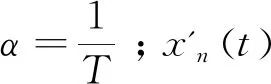
根据驾驶员对车头间距的两种跟驰情况进行分析，本文对车辆跟驰情况中的两种状态进行研究：①车间距较小时后车减速前进的跟驰模型；②车间距较大时后车加速前进的跟驰模型。设两车以相同速度v1匀速行驶，两车处于跟驰状态且车间距较大。在t0时刻前车在位置xn(t0)处以减速度an开始减速，此时后车在位置xn+1(t0)。

2.1 车间距较小时后车减速前进

后车认为两车间距足够大之前，仍以原有速度行驶一段时间T0，当后车认为两车间距快要接近安全车距时，才开始反应。经过反应时间T后，在t1=t0+T0+T时刻以减速度an+1开始减速，两车处于跟驰状态。前车经过时间Δtn(时刻t2=t0+Δtn)到达位置xn(t2)，而后车经过时间Δtn+1(时刻t3=t0+T0+T+Δtn+1)到达位置xn+1(t3)后，两车均以相同速度v2匀速行驶，继续保持跟驰状态，则

(2)

(3)

(4)

(5)

根据文献[7，9]的研究，引入需求安全距离L(vn+1(t))，其中，L是后车在时刻t的速度位移函数，为车辆跟驰中后车相对于前车保持的安全距离。

1) 如果T0+T+Δtn+1>Δtn，则

(6)

t0时刻两车的车头间距为

s(t0)=xn(t0)-xn+1(t0)

(7)

t3时刻两车的车头间距为s(t3)，则有s(t3)=xn(t3)-xn+1(t3)，即

(8)

则车辆跟驰需求安全距离模型为

(9)

2)如果T0+T+Δtn+1<Δtn，则

(10)

t2时刻两车的车头间距为s(t2)，则有s(t2)=xn(t2)-xn+1(t2)，即

(11)

则车辆跟驰需求安全距离模型为

(12)

2.2 车间距较大时后车加速前进

后车认为两车间距足够大之前，以am+1加速行驶一段时间T0，当后车认为两车间距快要接近安全车距时发现前车在减速，才开始反应，此时速度为v2′。经过反应时间T后，在t1=t0+T0+T时刻以减速度an+1开始减速，两车处于跟驰状态。前车经过时间Δtn(时刻t2=t0+Δtn)到达位置xn(t2)，而后车经过时间Δtn+1(时刻t3=t0+T0+T+Δtn+1)到达位置xn+1(t3)后，两车均以相同速度v2匀速行驶，后车继续保持跟驰状态，则

v2′=v1+am+1(T0+T)

(13)

(14)

(15)

(16)

(17)

1) 如果T0+T+Δtn+1>Δtn，则

(18)

t3时刻两车的车头间距为s(t3′)，则有s(t3′)=xn(t3)-xn+1(t3)，即

(19)

则车辆跟驰需求安全距离模型为

(20)

2) 如果T0+T+Δtn+1<Δtn，则

(21)

t2时刻两车的车头间距为s(t2′)，则有s(t2′)=xn(t2)-xn+1(t2)，即

(22)

则车辆跟驰需求安全距离模型为

(23)

3 稳定性分析

交通流稳定性的研究在交通流特性分析、交通安全及交通堵塞等方面有着重要影响[10]。在车流稳定运行时，当头车受到微弱的干扰，车流的整体运行态势会跟着发生改变。当扰动随着车辆行进间的传播随之消散，则车流是稳定的，反之则是不稳定的。假设稳态交通流相邻车辆的平均车头间距Se和稳态交通流中车辆速度ve有如下关系：

Xn(t)=(n-1)Se+vetn=1,2,…,N

(24)

式中：Xn(t)为车辆n在t时刻的平衡态位置；Se为稳态车流平均车头间距；ve为稳态速度；N为车辆数。

当头车在运行过程中受到微弱的干扰时，则有

yn(t)=ceiwrn+zt=xn(t)-Xn(t)yn(t)→0

(25)

(26)

式中：yn(t)为车辆n在t时刻的车间扰动；c为常数；xn(t)为车辆n在t时刻受到干扰后的位置；z为特征值；wr为第r个傅里叶展开参数，r=0,1,...,N-1。

对式(25)两侧求导得

(27)

式中：τn为反应时间。

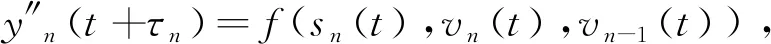
(28)

(29)

(30)

(31)

由式(28)—(31)可以得到

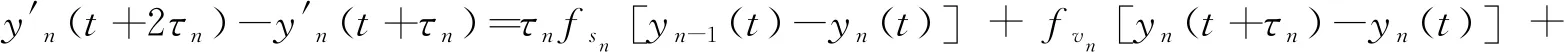
(32)

(33)

(34)

当z2<0时，交通流模型不稳定，反之，交通流模型稳定，故交通流稳定条件为

(35)

4 仿真分析

分析车流中车辆对其前车行为的反应能力对于估计驾驶环境的变化对交通状况的影响是很重要的。为解释这种行为，本文基于驾驶人反应特性的车辆跟驰行为的假设，构建了一个新的跟驰模型。该模型中的参数直接对应于驾驶员行为的明显特征，当在模拟中将实际值分配给参数时，模拟再现真实交通流的运行特征。通过MATLAB软件对车辆跟驰进行数值仿真，验证驾驶人由于车间距刺激项产生的反应对于车辆跟驰的影响。仿真系统中参数设置为：车辆最大速度Vmax=30 m/s；需求安全车距为8 m；车辆初始速度均为v=20 m/s；采样时间间隔t=0.1 s；反应时间T=1.0～1.5 s；车流为同步流。由于驾驶人的反应特性各不相同，只能在一定范围内变化，故通过反应强度反映驾驶人的反应特性，根据文献[11]的研究，对反应强度C=0.43，0.53，0.60进行取值模拟，分析不同反应强度值对于车辆跟驰速度、车间距的影响。

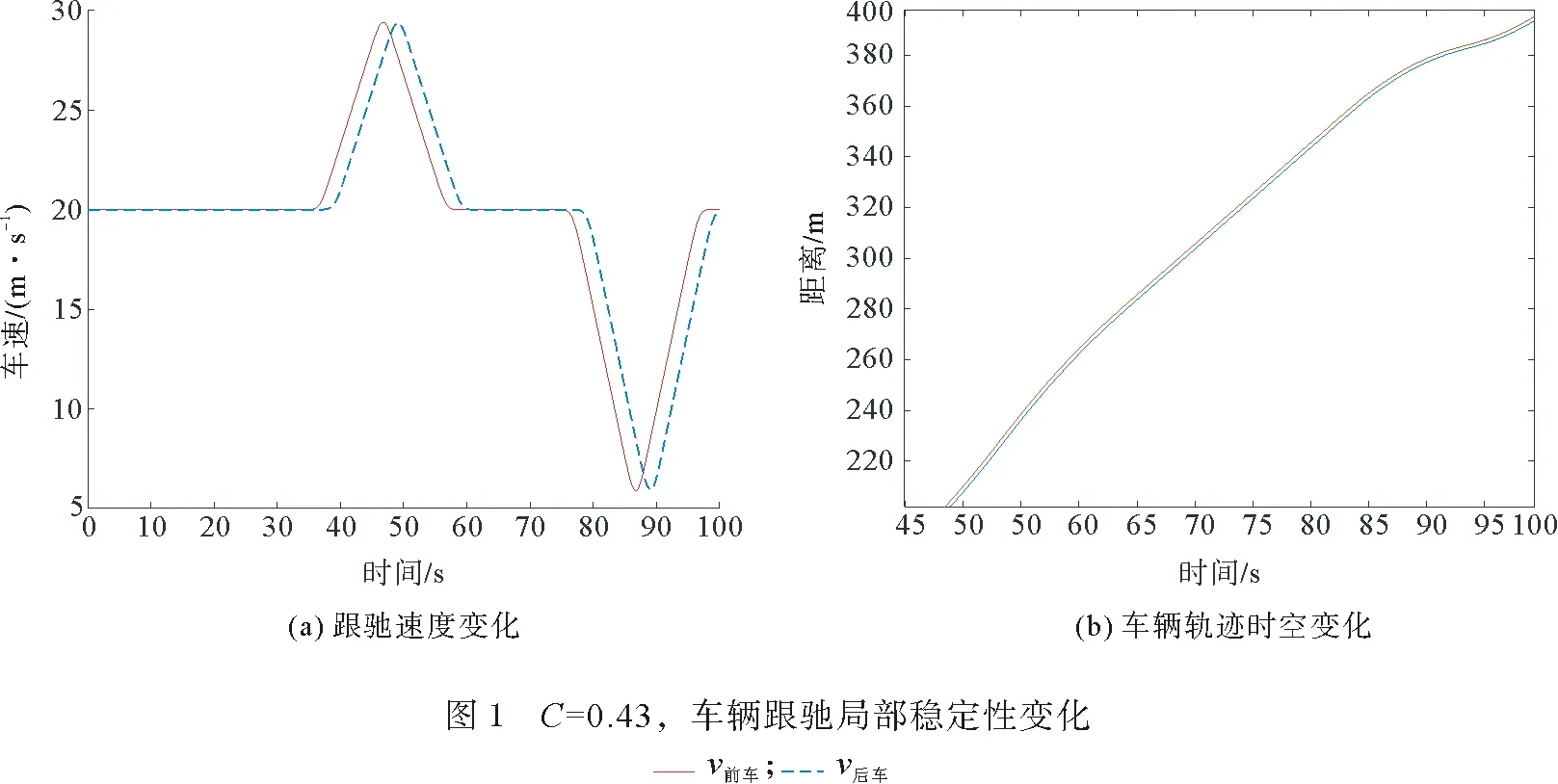
4.1 局部稳定性仿真分析

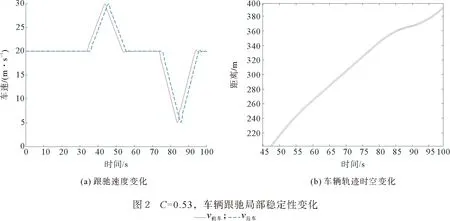
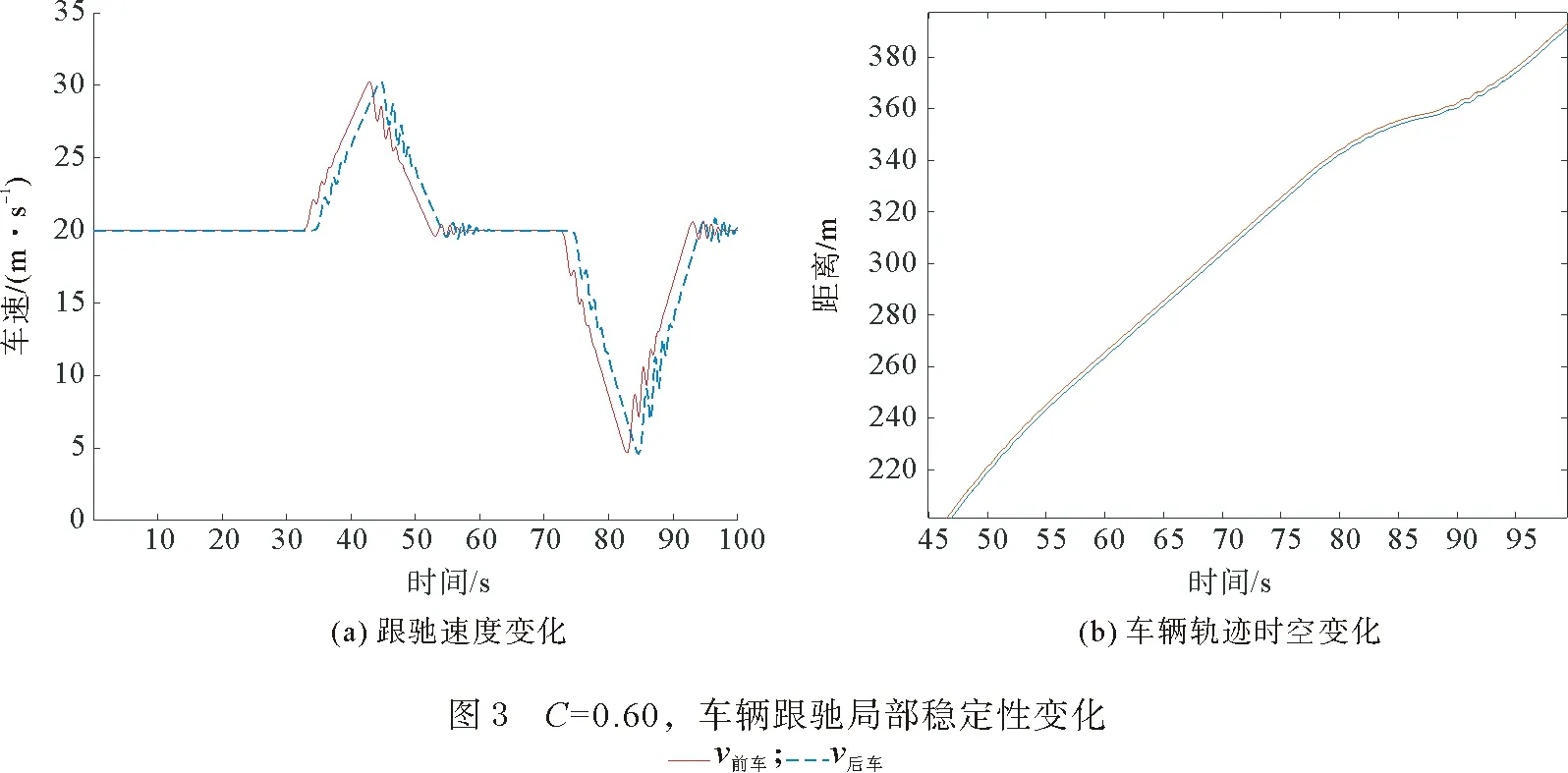
从图1—图3可以发现，随着反应强度的增加，跟驰车辆的速度与车头间距发生波动，而跟驰速度波动较为明显；从图3可以发现，反应强度达到0.60时，速度开始剧烈波动，车头间距振幅开始增大，车辆会发生追尾危险。

4.2 渐近稳定性仿真分析

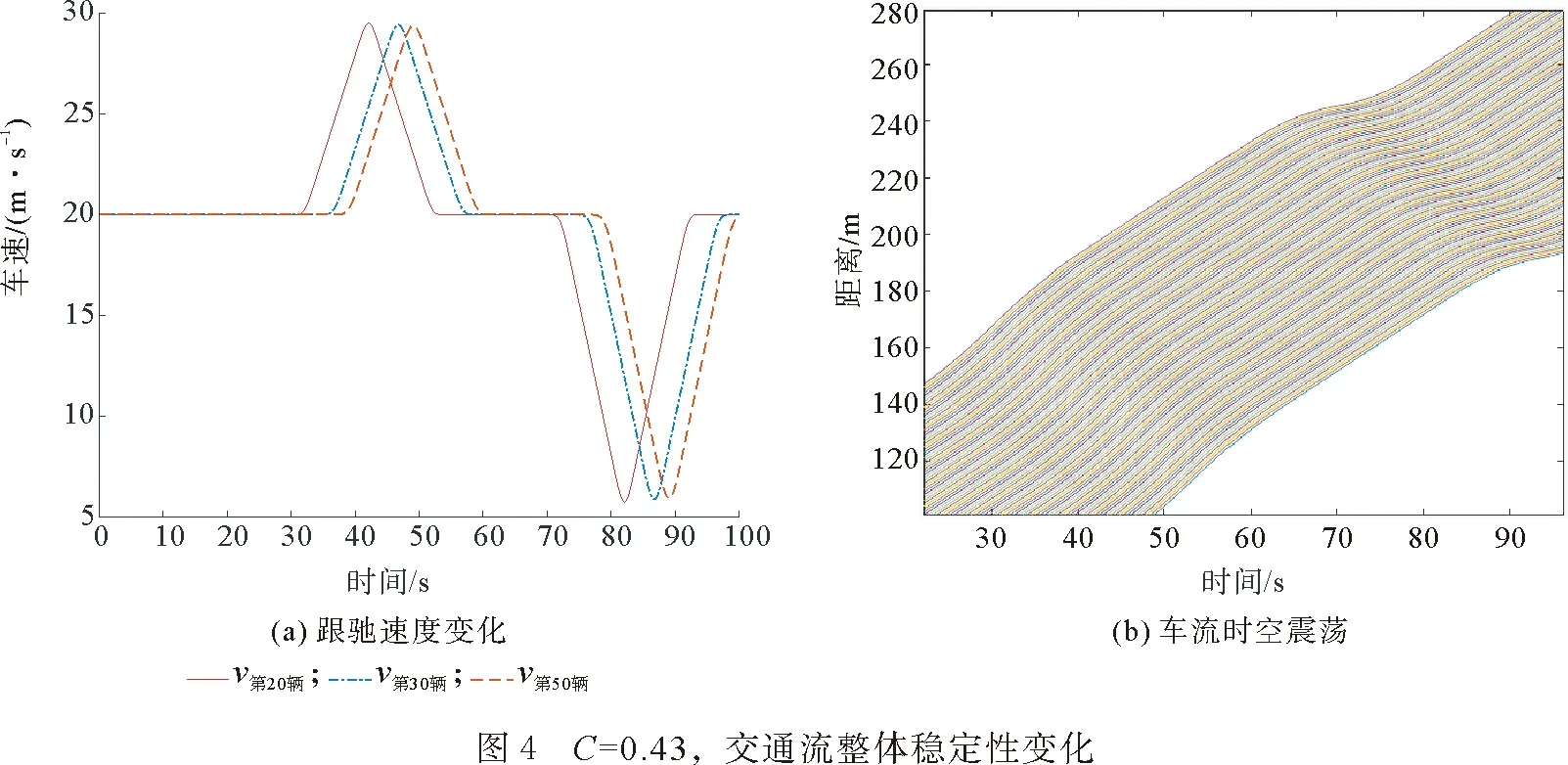
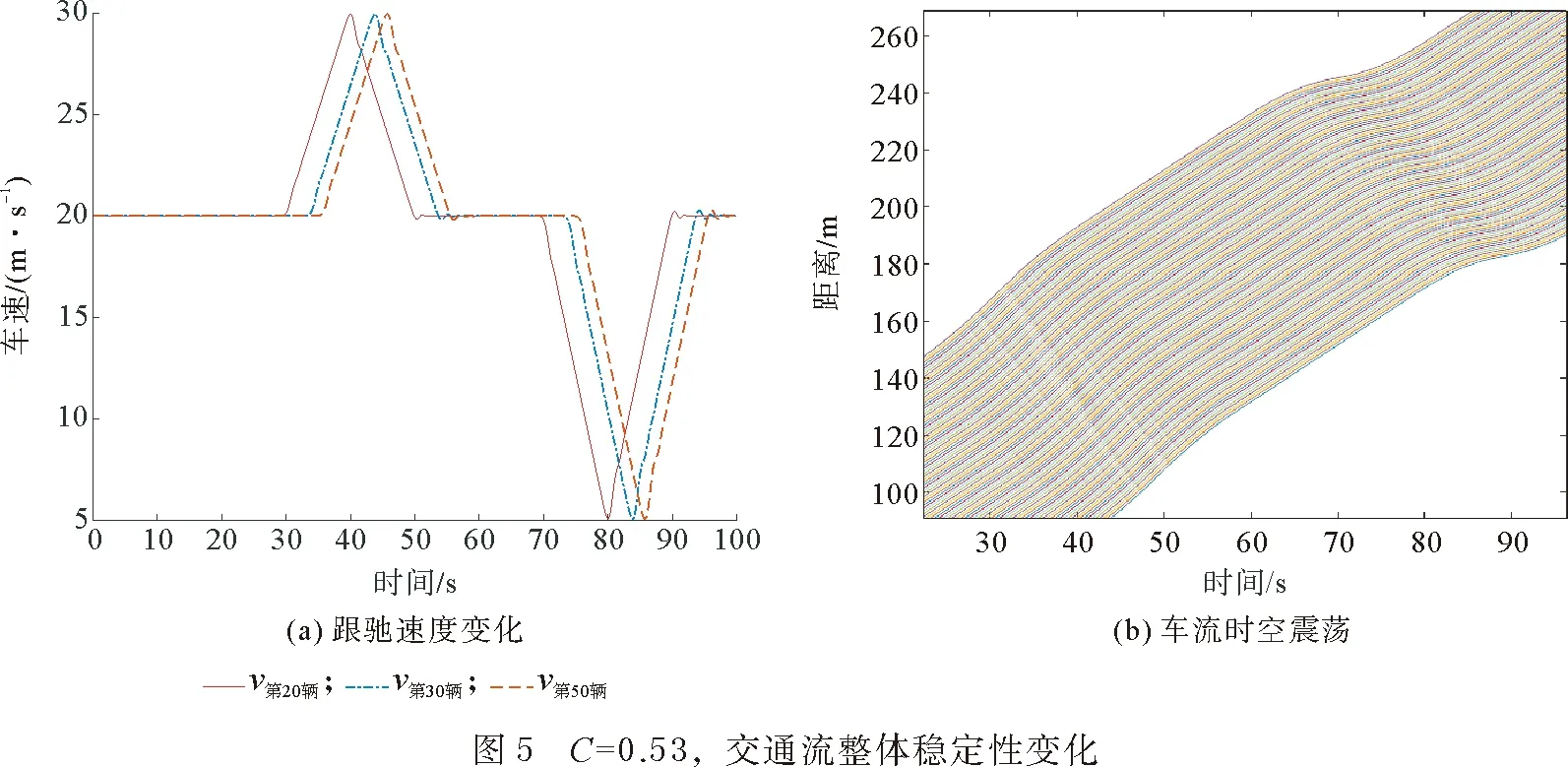
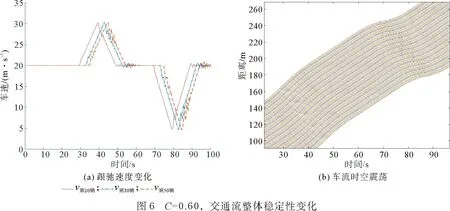
由图4—图6可以发现，在反应强度C=0.43时，跟驰车辆之间速度没有明显波动，交通流运行平稳。随着反应强度的增加，车辆的速度变化对上游车辆产生了一定影响，交通流整体速度开始下降。在反应强度C=0.53时车流开始从下游到上游出现轻微震荡，在反应强度C=0.60时车流剧烈震荡，容易引发交通流失稳。

5 结论

本文依据跟驰理论对传统跟驰模型进行研究，通过驾驶人对于跟驰过程中车间距变大或变小两种情况的反应进行分析，并对2种情况中的2个跟驰状态建立基于驾驶人反应特性的车辆跟驰模型。通过仿真能够客观准确地描述跟驰行为对交通流稳定性的影响，由道路中车辆之间跟驰行为产生的小扰动，从而进展成对交通流状态的影响，仿真结果表明，在同步交通流中，驾驶员跟驰反应越激烈，车流的状态越容易被破坏，甚至发生安全事故，从而演变成交通拥堵。基于驾驶人反应特性的车辆跟驰模型研究所涉及的速度、车间距及反应时间等参数对于正确理解驾驶行为，指导车路协同及无人驾驶的发展都具有很重要的意义。