云模型和集成极限学习机相结合的滚动轴承故障诊断方法
赵荣珍, 马森财, 吴耀春
(兰州理工大学 机电工程学院, 甘肃 兰州 730050)
滚动轴承是旋转机械的重要组成部分,其健康状态直接决定着整台机械设备乃至整条生产线能否正常运行.滚动轴承的振动信号本身具有非线性和非平稳性,且常常伴有随机噪声的干扰.对滚动轴承信号进行特征提取和状态识别是研究的关键[1-2].
针对滚动轴承振动信号样本量大、波动复杂等问题,许迪[3]提出基于流形学习和M-KH-SVR(multi-variable-krill herd-support vector regression)的滚动轴承衰退预测方法,通过多变量特征验证了模型的泛化性和预测精度.针对滚动轴承故障类别难以辨识的问题,赵荣珍等[4]提出的一种EWT多尺度排列熵和GG(Gath-Geva)聚类算法相结合的诊断方法,其聚类时的类内紧致性优于其他聚类算法.杨平等[5]针对传统深度学习网络对滚动轴承含噪信号辨识率较低的问题,提出一种基于卷积胶囊网络的故障诊断方法,该模型使用两个卷积层的卷积网络对原始信号进行特征提取,并将其送入胶囊网络,最终输出每种故障类型的诊断结果.
上述方法虽取得了一定的诊断效果,但是有一定的不足.首先,忽视了振动信号具有不确定性(模糊性,随机性)这一客观事实;其次,深度学习网络用于故障辨识时,网络的计算量大、硬件需求高、模型设计与搭建复杂,且深度学习网络对不平衡数据比较敏感.对于不确定性问题,云理论模型具有较强的适应性.近年来,该方法作为一种数据分析与概念表达手段已经在包括电力负荷预测、状态估计、变压器故障诊断等方面得到了较为广泛的应用[6-9].同样,作为一种能显著提高分类器分类精度的并行式决策方法,Bagging集成学习因其操作比深度学习网络简便,且识别效果明显,而被广大学者采用[10-11].
基于上述缘由,本研究将振动信号视为一个云团,采用改进的逆向云算法提取振动信号的期望、熵和超熵三个云特征参数,并将云特征参数作为集成极限学习机的输入参数,实现了对轴承故障的分类.最后,以实验验证了本研究方法的有效性.
1 相关理论简介
1.1 云理论及其指标
假设U是一个可以用精确数值表示的论域(维数可为一维或者多维的),H为U对应的定性概念,∀x且x∈U.存在一个具有稳定倾向的随机数y=μH(x),表示y是x对定性概念H的确定度.x在论域U上的分布称为云模型,简称云[12].
云的数字特征用期望Ex、熵En和超熵He来表征,这是定性概念的定量表示,对于理解定性概念的内涵和外延有重要的意义.它们的定义分别如下:
期望Ex(expected value)是云滴在论域空间的分布期望,就是最能代表定性概念的点.它们的定义分别如下:
熵En(entropy)是定性概念的不确定性度量,由概念的随机性和模糊性共同决定.
超熵He(eyper entropy)是熵的不确定性的度量,即熵的熵,由熵的随机性和模糊性共同决定.
1.2 改进的逆向云发生器
云发生器分为正向云发生器(forward cloud generator)和逆向云发生器(backward cloud generator)两种.正向云发生器是从定性到定量的映射,它根据云的数字特征(Ex,En,He)产生云滴(x,y).逆向云发生器是实现从定量值到定性概念的转换,它可以将云滴(x,y)转换为以数字特征(Ex,En,He)表示的定性概念.云模型如图1所示.
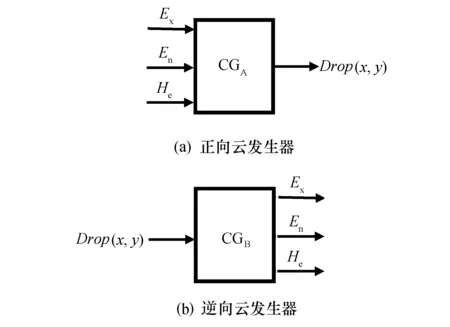
图1 云发生器模型Fig.1 Cloud generator model
现实中代表概念的确定度y值并没有给出或者难以获得,且传统逆向云算法难以向更高维推广.针对以上问题,杨薛明等[13]引入了一种无需确定度y的逆向云算法,该算法不仅简单、易于向高维推广,而且精度比原来的逆向云算法高.新的逆向云算法计算过程如下:
输入 无确定度云滴xi(i=1,2,…,N);
输出 表示云滴xi定性概念的期望Ex、熵En和超熵He;
(1)
(2)
(3)
1.3 极限学习机
极限学习机(extreme learning machine,ELM)属于误差前馈神经网络的一种[14],该算法旨在解决BP(back propagation)网络执行效率较低这一问题,属于有监督学习器的一种[15-16].根据ELM理论,有训练样本(xi,yi),其L1正则化目标函数可以定义为
(4)
s.t.WTh(xi)=yi-ξi
式中:h(xi)为对应的隐含层特征,假定有n维;W∈Rn×T为隐含层输出权值;ξi∈RT×N为训练样本的误差;T和N表示样本个数和类别数;C为正则化因子.
利用Lagrange对偶算法求得式(4)的最优解为
(5)
式中:Y为训练样本的输出矩阵.
测试样本xc在极限学习机上的分类输出为
f(xc)=W*Th(xc)
(6)
2 特征提取及分类模型建立
2.1 信号采集
本次实验的设备为无锡市厚德自动化仪表有限公司的HZXT-DS-001型双跨综合故障模拟平台,实物结构如图2所示.

图2 双跨双转子综合故障模拟平台 Fig.2 Double-span double-rotor comprehensive fault simulation platform
故障轴承安装端如图3所示.具体的故障轴承为NSK6308深沟球轴承,模拟的故障类型有4种,分别为内圈裂纹、外圈裂纹、滚动体损坏、保持架破裂.其中,内外圈故障都为深1.5 mm、宽0.2 mm的凹槽,滚动体故障和保持架故障用电火花加工而成,具体故障情况如图4所示.

图3 故障轴承安装端Fig.3 Fault bearing mounting end

图4 故障轴承的形貌特点Fig.4 Failure mode of fault bearing
为更完整地表征轴承的故障状态,共采集了5个通道的振动信号.前3个通道使用加速度传感器,采集含故障轴承在两个相互垂直的径向方向(x方向和y方向)和轴向方向(z方向)的振动信号,对应通道ch1、ch2、ch3;后2个通道使用电涡流传感器,采集故障轴承一侧轴的径向位移信号,对应通道ch4、ch5.采样频率设为8 kHZ,采样转速为3 000 r/min.采集4种故障状态和正常状态的信号各80组.
2.2 信号预处理及云特征提取
信号的小波包分解相当于让信号通过了一系列中心频率不同但噪声相同的滤波器,若给定信号的分解层数为k,则有2k个树分支.为消除噪声对轴承故障本征信号的影响,提高后续模式识别的准确性,对采集的原始故障信号进行sym4为基函数的4层小波包分解,以sure熵为准则得到小波包分解最佳树,选取第4层的前8个频段重构信号.最佳小波树如图5所示.

图5 最佳小波树Fig.5 Best wavelet tree
经小波包分解后的重构信号如图6所示,各状态下重构信号经云化之后对应的云模型如图7所示.图7中隶属度是衡量确定性程度的量,该值无具体单位.对重构后的振动信号,采用1.2节所提到的逆向云算法提取决定信号云的云特征参数期望、熵、和超熵,依此构造出轴承的故障特征数据集.由于有5个通道同时采集实验台不同部位的信号,故可得到3×5=15维的原始故障特征集.为便于后续模型分类的实现,对原始数据进行归一化处理.预处理后部分故障数据的前3个通道特征如表1所列.

表1 归一化后部分故障数据的前3个通道云特征对比
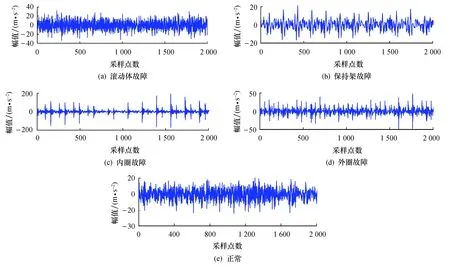
图6 滚动轴承在不同状态下的振动信号Fig.6 Bearing vibration signal in different states

图7 不同状态下的振动信号的云模型Fig.7 Cloud model of bearing vibration signal in different states
2.3 集成极限学习机模型的建立
极限学习机虽然训练和计算速度快,但和大多数神经网络一样,其分类精度依赖于隐含层节点的合理选取,而且即使在网络结构和训练集不发生改变的情况下,对于同一测试集,极限学习机每次的分类准确率都在跳动,即准确率的稳定性很差.本研究将Bagging集成学习算法引入其中,利用弱学习理论,使得多个在分类错误上具有一定独立性的极限学习机统一参与轴承故障的分类,最终分类结果用相对多数投票法得到.需要注意的是,在训练E-ELM时训练集的标签要用1至5的字符量表示.基分类器预设数目为30个, 极限学习机的激活函数规定为sigmoid函数.
极限学习机隐含层神经元最佳数目k的确定采用了实验法.即先从经验公式中求得极限学习机模型隐含层所需节点个数的最小值,并以1为增量增加隐含层的节点个数,同时得到不同隐含层节点数目下的分类误差e,最后利用二次多项式拟合出极限学习机隐含层节点数和分类误差之间的函数曲线图.ELM的隐含层节点数与集成ELM的隐含层节点数和各自分类误差的关系如图8所示.
从图8可以看出,在隐含层节点相同的情况下集成极限学习机具有更好的分类精度,集成极限学习机的隐含层节点数确定为10个.在确定了隐含层节点的情况下,以分类误差不高于0.05为原则改变基分类器数目的预设值.经验证,基分类器的原预设值满足实验要求.至此,E-ELM的两个超参设置完成.

图8 节点数对两种分类器分类误差的影响
建立的集成极限学习机算法步骤:
输入 云特征的训练集T和测试集U;
输出 故障类别集S;
1) Fori=1,N为基学习器数目
(1) 对训练集T采用Bagging方法中的重采样算法,得到训练子集Ti;
(2) 利用训练子集Ti训练出极限学习机,得到Hi;
(3) 将测试集E输入至Hi,得到结果Si;
2) 对于Si利用相对多数投票法得到最终分类结果S.
以ELM为基学习器的Bagging集成学习模型如图9所示.从中可以看出,直接输入至各ELM训练集都是初始训练集经自助采样法得到的子集,测试样本最后的分类结果由30个ELM共同投票得到.

图9 以ELM为基学习器的集成学习模型Fig.9 Ensemble learning model based on ELM
3 模型应用及分析
3.1 轴承故障分类
将轴承的云特征数据集输入到2.3节建好的分类模型中,以30次分类准确率的均值代表最终的分类准确率,以准确率的方差表征分类方法的稳定性.
将BP神经网络、极限学习机、支持向量机(support vector machine,SVM)、k近邻(k-nearest neighbor,KNN) 分类器与本研究所提的E-ELM算法进行对比,验证不同分类器对于云特征的识别情况.在实验过程中,BP网络的隐含层为1层,隐层神经元数目设为12,训练最小误差为0.1,训练次数为1 000次;为实验考虑,ELM的隐层神经元数目和E-ELM隐层神经元数目一样为10;SVM的惩罚系数和核参数用交叉验证法选取,寻优区间统一设置为[-10,10]; KNN分类器的近邻样本数目设置为6.E-ELM和ELM及其他分类方法在滚动轴承故障分类上的对比如表2和表3所列.

表2 ELM和E-ELM在滚动轴承故障分类上的对比

表3 E-ELM和其他分类方法在滚动轴承故障分类上的对比
从表2和表3可知,本研究所提之E-ELM算法在云特征数据集上的识别率均高于传统分类算法.从执行时间来看,虽然E-ELM分类方法是以消耗时间为代价来提高其分类准确率,但仍然在可接受的范围(支持向量机执行时间最高的原因是记入了参数寻优的时间).E-ELM方法分类性能较好的原因分析如下:
1) Bagging集成学习算法中,理论上只要基分类器的分类误差不小于1/k(k为类别数),就可以通过不断增加基分类器的方法让识别率无限接近于100%.因此,E-ELM在多个ELM参与的情况下获得了较高的识别精度.
2) 在执行效率方面,由于作为基分类器的ELM本身的执行效率较高,且数据集特征的维数也较低,所以即使集成学习过程消耗了时间,但整体上E-ELM的执行效率也较好.
3.2 E-ELM在变工况下的识别能力
旋转机械在工作时转速经常会变化,为验证E-ELM方法是否在不同工况下具有良好的识别精度,分别在2 600、2 800、3 200 r/min的云特征数据集上进行验证.在不同的轴承工作转速下E-ELM方法仍具有较高的识别精度,结果如图10所示.

图10 E-ELM方法在变工况下的识别精度Fig.10 Identification accuracy of E-ELM method under variable working conditions
3.3 E-ELM的抗噪性验证
实际情况下获得的数据集会由于环境的干扰含有大量的噪声,为验证建立的E-ELM模型的抗噪能力,在测试集中加入随机扰动.扰动矩阵定义为M=0.2·F(120,15).其中,F为随机函数,指在产生区间为[0,1]的随机数;120表示测试样本的数量为120个,15表示测试集特征参数的个数为15个.E-ELM方法与其他分类方法在抗噪性方面的对比如表4所列.
从表4可知,E-ELM分类方法与其他传统的神经网络相比具有更好的抗噪性.故本研究所建立的云E-ELM方法在滚动轴承故障辨识领域有良好的工程实用价值.
3.4 云-集成极限学习机对不同程度不平衡故障的辨识能力
为验证基于云-集成极限学习机算法的适用性,在图2所示的双跨双转子实验台上模拟了6种不同程度的不平衡状态.从左起第一个质量盘命名为P1,第二个质量盘命名为P2,在盘上添加若干质量为12 g的不平衡质量块,模拟不同程度的不平衡,如表5所列.
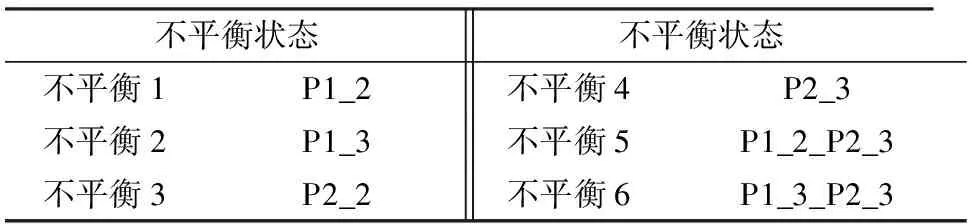
表5 不平衡状态
表5中,“P1_2”表示在质量盘P1上添加2个质量块;“P1_2_P2_3” 表示在质量盘P1上添加2个质量块,在质量盘P2上添加3个质量块.实验过程中,对于单个质量盘来说,质量块分布位置应相对集中,两个质量盘上的质量块成180度分布.此次实验采样转速分别为3 000、3 200、3 400、3 600 r/min,采样频率为20 kHz.云-集成极限学习机算法在转子不平衡故障数据集上的分类效果如表6所列.
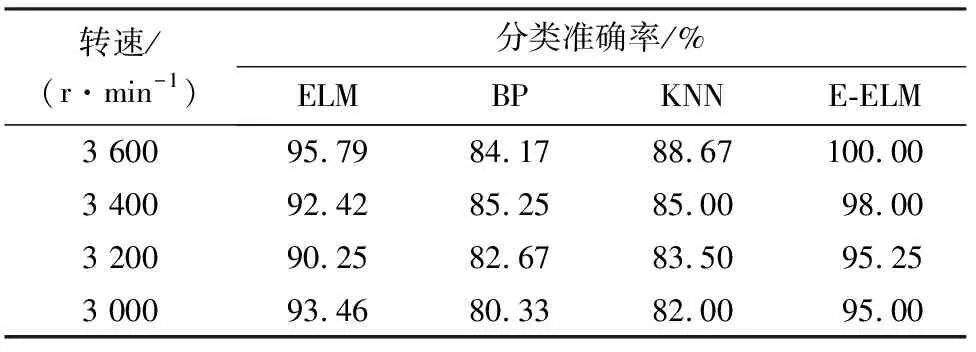
表6 云-集成极限学习机算法在转子不平衡故障数据集上的分类效果
从表6可知,本研究方法对转子不平衡故障的辨识能力较好,具有一定的普适性.
4 结论
本研究提取了滚动轴承故障信号的云特征,将含云特征的数据集引入到了建立的集成极限学习机模型中去,实现了轴承故障的人工智能辨识.实验表明,提取的滚动轴承云特征数据集可以良好地表征各类故障状态,所建立的分类模型在分类准确率上有了较大的提升.与ELM方法相比,在隐含层节点一致的情况下,集成极限学习机的分类稳定性和分类精度更高且具有良好的抗噪性.本研究提出的模型能有效地识别滚动轴承的故障类型,它为旋转机械的故障模式辨识提供了一种新的思路和手段.下一步的工作中,将直接构造出云分类器来实现轴承故障的辨识.

