Cu/Al共掺ZnO光学性质的第一性原理计算
李维学, 高姗姗, 戴剑锋,2, 索忠强, 王 青,2
(1. 兰州理工大学 理学院, 甘肃 兰州 730050; 2. 兰州理工大学 省部共建有色金属先进加工与再利用国家重点实验室, 甘肃 兰州 730050)
ZnO是一种直接宽带隙化合物半导体材料,其激子束缚能为60 mV,激子增益达320 cm-1,而且ZnO材料成本低廉,易于制造,抗辐射能力强,在LEDs、LDs[1-3]、太阳能电池板[4]、传感器[5]和液晶显示[6]等领域具有十分重要的应用前景.但由于其带隙较宽,电导率很低且对可见光不敏感等问题,限制了其在光电子领域诸多方面的应用.通常可以通过掺杂改善ZnO的光电性质,以达到不同领域的需求.Qu等[7]采用双靶溅射法在Si(100)和石英基片上制备了Cu掺杂ZnO薄膜,发现其光学带隙随着Cu掺杂量的增加有所减小;Hao等[8]使用直流与射频双靶共溅射法制备了Cu掺杂ZnO的薄膜,结果表明,在一定范围内随着Cu溅射功率的提高,薄膜的结晶质量也会提高,一旦超过此范围就开始降低,透过率则一直减弱;Wang等[9]基于密度泛函理论计算了Cu掺杂BN薄膜,随溅射功率的提高,其电阻率降低,光吸收边向短波方向移动;N.Boukhenoufa等[10]用溶胶-凝胶法制备了Al掺杂ZnO薄膜,掺杂质量分数为5%时其光电性能较好,电阻率为1.6 Ω·cm;Jessica等[11]用溶胶-凝胶法制备了Al掺杂ZnO纳米颗粒,随着掺杂量的增加,光吸收向可见光区域移动;D.Sengupta等[12]通过控制Al掺杂ZnO的浓度,得到了高光转换率的颗粒;M.Maache等[13]用自旋涂层法制备了Al掺杂ZnO的薄膜,发现其可见光范围内的透射率大于75%;Sreedhar等[14]采用磁控溅射法制备了Al掺杂的ZnO,外加磁场时,紫外光区和可见光区光透率达90%;Liu等[15]利用化学气相沉积法制备Al/N掺杂ZnO薄膜,350 ℃时薄膜透过率为65.7%;Yang等[16]利用磁控溅射法,制备了掺杂比例不同的Cu/Al共掺ZnO薄膜.向薄膜中掺杂Cu/Al能够降低ZnO薄膜的电阻率,相同长度的铜丝和铝丝共掺时,对其在可见光范围内的透过率几乎没有影响.
综上,Cu掺杂或者Al掺杂ZnO已经得到了较为广泛的研究,Cu/Al共掺ZnO的光电性质也在实验中得到了探讨,但是目前还缺少共掺的理论计算,共掺的本质需进一步讨论.本文主要对Cu/Al共掺ZnO的电子结构和光学性质进行理论计算与分析,从微观层面解释宏观实验现象.因为Cu离子存在变价,此处需做讨论,若Cu+替代Zn2+会产生空穴,变成受主能级,此时所选取的原胞不能屏蔽周期性边界条件下的库仑耦合效应.但Cu/Al共掺杂时,由于Al3+和Zn2+的化学价不同,所以替位后体系中会有额外的正电荷,额外的正电荷会对临近Cu+进行电荷补偿,将其氧化成Cu2+.
1 模型和方法
1.1 理论模型
自然条件下纤锌矿结构的ZnO最稳定,它属于P63mc空间点群[17],其晶胞由Zn的六角密排和O的六角密排在c轴方向平移嵌套而成.实验中ZnO的晶格常数为a=b=0.324 9 nm,c=0.520 6 nm,c/a=1.602,α=β=90°,γ=120°.先对所建立的2×2×2本征ZnO超晶胞进行几何优化,再用Cu原子和Al原子替换ZnO中的Zn原子,对其电子结构和光学性质进行第一性原理计算.图1为晶格优化后Cu-Al共掺杂ZnO的超晶胞结构图.

图1 晶格优化后Cu-Al共掺ZnO的超晶胞(2×2×2)模型Fig.1 Supercell(2×2×2)model of Cu-Al doped with ZnO after lattice optimization
1.2 计算方法
基于密度泛函理论[18]的Material Studio 2017软件中的CASTEP模块,即从头算量子力学程序[19],将电子间相互作用的交换-关联能转化为电子密度形式.计算中忽略了内层核心电子、价电子的运动波与离子实的波函数正交且在原子核附近变得平滑[20],使用周期性边界条件,利用平面波基矢组将电子波函数扩展[21],就可以把平面波基矢的数量减少,从而减少计算量.交换-关联势采用广义梯度近似(GGA)[22],GGA比局域密度近似(LDA)[23]计算结果更加精准可靠.在迭代计算过程中每个原子平面波能量的收敛精度为1×105eV,作用在每个原子上的相互作用力的收敛精度为0.03 eV/nm,晶体的内应力小于0.05 GPa,原子的公差偏移为0.001 nm,计算中选取的倒易空间平面波截断能为Ecut= 400 eV,布里渊区中优化结构和计算总能量的K-Point均为4×4×2,计算中选取的O、Zn、Cu和Al原子的价电子组态分别为O-2s22p4,Zn-3d104s2,Cu-3d104s1和Al-3s23p1.
2 结论和分析
2.1 晶体结构
表1为晶格优化后的本征ZnO和各掺杂ZnO体系的晶格参数与形成能.从表1可看出,本征态ZnO优化后的晶格常数与文献[24]一致.因为采用替位掺杂,所以对ZnO纤锌矿结构无影响[25],各种掺杂体系对ZnO的晶胞参数有略微的影响,优化后本征态c/a=1.607,和实验值1.602误差仅为0.31%,说明晶格没有发生畸变,此计算方法可靠.掺杂后的ZnO晶胞体积减小,这是由于掺杂离子半径小于Zn2+半径导致(离子半径:aZn2+(0.74 nm)>aCu2+(0.73 nm)>aAl3+(0.53 nm)).Al3+替换Zn2+时,体系中产生了额外的正电荷,它们之间的排斥作用导致系统能量升高进而体积增大[26],所以Cu-2Al掺杂体系的体积变大.并且额外的正电荷会给Cu+提供补偿作用,导致正电荷数目减少,系统排斥力减弱.相较于2Cu-Al体系而言,Cu-2Al体系中用于提供电荷补偿的正电荷少,所以排斥力较大.综上,2Cu-Al体系体积最小.相较于Cu、Al单掺,共掺形成能更低,则体系更易形成,说明此共掺体系的共掺粒子溶解度高、且ZnO中的载流子浓度较高.Al单掺比Cu单掺结构更稳定,所以共掺时Cu-2Al体系最稳定,掺杂最容易.这与文献[15]分析的结果一致.

表1 晶格优化后的本征ZnO和各掺杂ZnO体系晶格参数与形成能
表2为晶格优化后本征ZnO和各掺杂ZnO体系原子间的重叠集居数的平均值,从表2中可以看出,O—Zn键的集居数变化幅度不大,本征ZnO的O—Zn键以共价键为主,夹杂着离子键.掺杂原子会影响其周围原子间的成键,会重新分配体系电荷.晶体有各向异性,所以掺杂后晶体中各方向上的成键情况不同[19].O—Cu键和O—Al键分别相较于O—Zn键,发现:在平行(∥)于c轴方向上,O—Cu键集居数减小,共价性减弱,离子性增强;O—键集居数增大,共价性增强,Al浓度大的集居数大.在垂直(⊥)于c轴方向上,Cu浓度最大时,O—Cu键集居数稍有增大,共价性增强;O—Al键集居数增大共价性增强,Al浓度大的集居数小.相较于单掺,共掺后平行于c轴的O—Cu键集居数大幅减小,表明Al的掺入使O-Cu键离子性增强,即Al的掺入使得Cu原子周围的电子云密度减小,体系中出现Cu+、Cu2+.

表2 晶格优化后本征ZnO和各掺杂ZnO体系原子间的重叠集居数
2.2 能带结构和态密度分析
图2为本征ZnO和各掺杂ZnO体系的能带图,图中0 eV的虚线表示费米能级.因为只有费米能级附近的部分电子参与导电,所以为了方便分析,图中仅给出了费米能级附近(-4~4 eV)的能带结构图.由图2a可以看出,本征ZnO带隙Eg=0.804 eV,此结果与文献[19]的计算结果一致.它比实验值Eg= 3.37 eV偏小,是因为CASTEP计算材料带隙时采用的GGA会把Zn-3d态电子能量过高的估算[27],以至其与O-2p态电子的相互作用能增大而导致价带变宽,带隙减小[28-29],采用该计算方法普遍存在此问题,但不影响对其理论分析[30].如图2b所示,相较于本征ZnO,Cu单掺ZnO后价带变得更为平缓,导带向费米能级移动,带隙宽度减小.图2c为Al单掺ZnO的能带图,可以看出,导带和价带均发生了较为明显的移动,费米能级向上移动,进入导带底部.在Cu-Al掺杂体系中,Al的引入使得体系中导带载流子浓度增加,能带下移,如图2d所示.但Cu的引入使得导带大幅上移且在带隙中出现与导带相连的杂质能级,费米能级进入导带;图2e为2Cu-Al掺杂体系,与图2d相比,因增大了Cu的占比,导致其导带和价带继续略微上移,带隙中出现了更为复杂的与导带相连的杂质能带,米能级出现在杂质能带靠上位置;图2f是Cu-2Al掺杂体系,相比于图2d,因其增大了Al的占比,导致导带和价带下移,带隙中出现了与图2f相似的杂质能带,费米能级进入导带,各掺杂体系都属N型且能带结构都变得平缓,说明各体系比较稳定,与之前的形成能计算相辅.
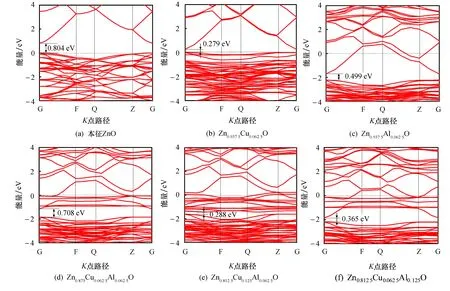
图2 本征ZnO和各掺杂ZnO体系的能带图Fig.2 Energy band structures of pure ZnO and doped ZnO system
图3为本征ZnO和各掺杂ZnO体系的态密度图,本征ZnO的价带分为两部分,-6.5~0 eV主要是由O-2p态和Zn-3d态轨道杂化形成,-18.3~ -16.5 eV则由O-2s态形成,如图3a,导带主要由Zn-4s态形成.共掺时,Cu的引入主要作用在带隙而Al主要作用在导带.相较于本征ZnO的图3a,图3b中Cu单掺杂后的主峰几乎没有运动,但在0.62 eV下产生了Cu-3d电子的杂质峰,表明Cu-3d作用于带隙以产生杂质能级.虽然Al单掺图3c在带隙中不产生杂质能级,但大量存在Al-3p电子导致导带的载流子浓度增加,能带结构明显向下移动.共掺体系图3d~3f的态密度图向低能方向移动,这是因为掺杂粒子中Al-3p轨道电子比Zn-4s轨道电子的能量更低,Al-3p轨道与O-2p轨道电子形成的类p反键比本征ZnO中的类s反键能量低,所以Al-3p轨道向低能方向移动[31],由文献[25]可知,p-p轨道之间相互作用时,会使价带向低能方向移动,而p-d轨道间相互作用时,会产生排斥,使得价带向高能方向移动.在共掺中,因为Cu的引入,使Cu-3d电子轨道与O-2p、Al-3p轨道发生排斥作用,所以能带会向高能方向移动,且会在带隙中产生杂质能级,又因p-d轨道的排斥作用较小,则对整体而言,能带向低能方向移动且导带移动幅度较大,所以带隙减小;各掺杂均在-20附近产生一个峰,这是因为Al-3s和3p态电子与O-2s之间的跃迁所致,费米能级附近有新的峰出现,这是因为Cu的引入使得费米能级处轨道杂化变多,产生新的能级;相较于图3d,当2Cu-Al掺杂时,如图3e,由于Cu浓度的增大导致杂质能级Cu-3d态电子浓度增加,使得p-d轨道间排斥增大,能带向高能方向移动且导带变宽,带隙减小;当Cu-2Al掺杂时,如图3f,由于增加了Al浓度,则能带向低能方向移动且导带和价带变宽,带隙也减小.掺杂浓度数量级大于1018cm-3时,就被认为是高掺杂的半导体.计算的掺杂浓度数量级为1021cm-3,由于泡利不相容原理,体系中电子由低到高依次排列,服从费米分布,为简并半导体.高掺杂半导体杂质浓度对迁移率的影响较大,迁移率不是常数[17],就电导率而言,它的掺杂率越小电导率越高.共掺时Cu-3d态和Al-3p态共同增加了费米能级附近的载流子浓度.载流子浓度、载流子迁移率和有效质量大小共同影响体系的电导率.由文献[25]可知,有效质量与带隙宽度成正比,结合能带图可知,各掺杂体系有效质量减小,则载流子迁移率变大,其电导率增加,这与文献[16]结果一致.
2.3 光学性质
研究极化方向为(100)面的光学性质.图4为本征ZnO和各掺杂ZnO体系的介电函数虚部,介电函数虚部直接关系着体系光学性质.由于CASTEP计算的带隙值比实验值(3.37 eV)小,所以在计算光学性质时引入了值为2.566 eV的剪刀算符对带隙进行修正,虽然使用剪刀算符有误差,但是变化趋势一致,不影响分析结果.由图4可知,本征ZnO的虚部谱中有3个主要的峰,分别在4.4、9.2、13.2 eV处,与文献[19]的结果一致,峰值来源该文献已经做了报告,这里不再赘述.单掺杂对介电函数虚部高能区有一定影响,共掺杂对该区域产生的影响较小,但都使低能区发生红移.Cu单掺红移最明显,这是因为Cu的引入在带隙产生了杂质能级,减小了电子跃迁所需的能量.Cu-Al掺杂体系在3.0 eV处出现峰值,表明掺杂使得杂质能带载流子浓度增加,跃迁增加;2Cu-Al掺杂体系在2.8 eV处出现最高峰且红移较多,是因为掺杂的Cu浓度最高,费米能级附近的载流子浓度最高,电子跃迁最多;Cu-2Al掺杂体系红移较小,在3.5 eV处出现峰值,是因为Al浓度较高使导带近满或全满,近满导致电子跃迁到导带所需能量增加,全满则电子不能跃迁至导带.又因费米能级处的载流子浓度相比于2Cu-Al体系较小,该体系红移减弱、吸收峰减小.
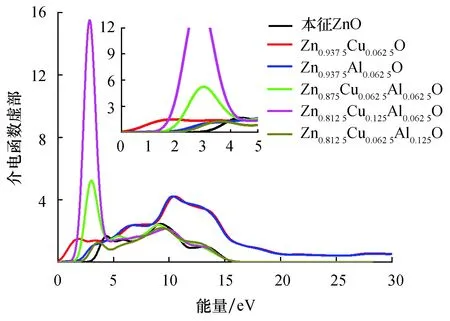
图4 本征ZnO和各掺杂ZnO体系的介电函数虚部Fig.4 Imaginary parts of dielectric functions of pure ZnO and doped ZnO system
图5为本征ZnO和各掺杂ZnO体系的光吸收谱.由图5可看出,相较于本征ZnO,各掺杂体系在低能区ZnO的光吸收均发生红移,Cu、Al单掺杂在高能区吸收明显增强,在13.9 eV处出现峰值,并且在可见光范围内吸收也增强,这是因为杂质能级作为带隙的跳板,使得VBM电子过渡到CBM所需的能量减少,促进了电子跃迁;Cu-Al掺杂体系和2Cu-Al掺杂体系都在3.3 eV处出现峰值,两者均可被红光激发,但后者峰值最高、光吸收最强;Cu-2Al掺杂体系在3.9 eV处出现峰值,可被黄光激发且光吸收最小,产生这些情况的原因与介电函数虚部峰值原因一致.

图5 本征ZnO和各掺杂ZnO体系的光吸收谱
图6为本征ZnO和各掺杂ZnO体系的光反射谱.从图6可知,相较于本征ZnO,掺杂体系在可见光范围内反射率均有增加,反射率与光吸收一致,吸收强的体系反射也强.光吸收、光反射和光透射遵从能量守恒原理[19],所以,光吸收与反射越弱则透射越强.结合图5、图6可知,各共掺体系中,Cu-2Al掺杂体系的透光率最高,这与文献[16]实验的的结果一致.

图6 本征ZnO和各掺杂ZnO体系的光反射谱Fig.6 Optical reflection spectra of pure ZnO and doped ZnO system
3 结论
用CASTEP软件对本征ZnO和Zn1-x-yCuxAlyO体系ZnO进行了第一性原理计算.通过优化晶体结构、计算能带结构、绘制态密度图和光学性质图进行分析.结果表明:掺杂后各体系的体积变化微小,Cu单掺红移最明显,2Cu-Al掺杂体系体积最小;掺杂使得ZnO中O—Al键共价性增强,O—Cu键离子性增强(除当Cu浓度最大时,c轴方向的共价性略有增强外);各掺杂体系均在带隙产生杂质能级且带隙减小,电导率增加;2Cu-Al掺杂体系在可见光范围内光吸收最强,可用于制造太阳能电池板光电极材料或者其他导电且光吸收率高的材料;Cu-2Al掺杂体系在可见光范围内的透光性最好,可用于制造导电且高透光的薄膜材料等.所以可以通过控制共掺比例来改善ZnO的电学和光学性能.

