基于分离涡模拟的核主泵水力性能非定常特性分析

王秀勇, 杜永峰, 汪东山, 吕 雪, 黎义斌

(1. 兰州理工大学 能源与动力工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省流体机械及系统重点实验室, 甘肃 兰州 730050)

核主泵的组成结构都是非常类似的,都是由叶轮、导叶、压水室这三个主要过流部件构成.由于受到叶轮与导叶之间的动静干涉作用,所以核主泵内流场具有较为强烈的非定常特性.流场中存在大量强度与尺度不同的旋涡结构,这些涡流结构的非定常变化会对机组的振动产生一定影响.因此,探究核主泵内部流动机理,研究其水力性能的非定常变化特征,并结合内部流场中涡核分布的瞬时变化规律进行共同分析,是十分必要的.

长期以来,关于泵的减振降噪研究一直是众多研究人员所关注的重点.从目前研究来看,叶轮与压水室之间周期性的干涉、不稳定的入流条件等均会引起泵内压力随时间的非定常变化,即压力脉动.压力脉动的非定常变化对机组的振动会产生一定影响[1-6].同时,泵在不同流量工况、输送两相介质时,由于动静干涉影响其内部旋涡运动具有明显的非定常特性,所以瞬时变化的旋涡结构对泵的性能会造成一定影响[7-11].目前国内外研究人员将关注点多集中在压力脉动、旋涡运动等非定常变化的方面,而很少着眼于探究泵的瞬时水力性能的非定常变化过程.

本文基于DDES湍流模型,对核主泵在一个旋转周期内其水力性能的非定常变化特性进行探究,并采用Q准则对泵内流场中的旋涡结构进行识别,探究内流场中旋涡结构的发展演化过程对水力性能的影响.通过以上探究,以期为核主泵的进一步优化研究提供有价值的参考.

1 计算模型及数值计算过程

1.1 几何模型

本文以快堆二回路钠泵原型样机为研究对象.其设计工况点流量Qd=630 m3/h,扬程H=35 m,转速n=990 r/min,比转速ns=105；叶轮叶片数为6枚,导叶叶片数为10枚.其计算域包含进水段、叶轮、导叶、球形压水室、口环及叶轮前后腔.计算域模型如图1所示.

图1 计算域模型Fig.1 Computational domain model

1.2 网格划分

利用ICEM软件对各过流区域进行六面体结构化网格划分.其中在进行壁面法线方向上的边界层网格划分时,给定第一层网格高度为0.05 mm,网格增长率设置为1.2,并设定边界层网格总层数为10层.为减小因网格数对计算结果产生的影响,以扬程计算结果进行网格无关性验证.当网格总数量在970万左右时,计算出的扬程值基本保持不变,由此确定出该计算模型的网格总数量为970万,计算域网格如图2所示.由于不同的湍流模型对近壁面网格尺寸要求不同,所以通常用无量纲壁面函数y+来表示,统计该泵全部过流部件近壁面y+值的分布范围,结果如图3所示.可以看出,y+值主要分布在5～20之间,基本满足DDES湍流模型对y+值的要求.

图2 计算域网格Fig.2 Mesh in computational domain

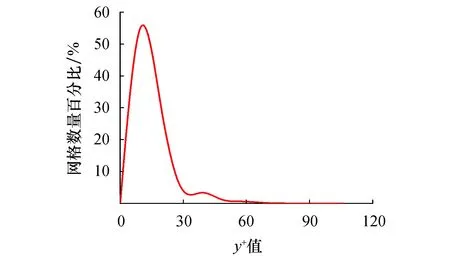
图3 壁面y+值分布图Fig.3 Distribution of wall y+ values

1.3 边界条件及定常与非定常计算设置

采用有限体积法对控制方程进行离散.压力与速度的耦合采用SIMPLEC算法,入口给定速度边界条件,出口给定自由出流边界条件,壁面采用无滑移壁面边界条件,静止域与旋转域之间的数据传递采用交界面边界条件.将RNGk-ε湍流模型的定常计算结果作为DDES湍流模型的初始流场并进行非定常计算.将叶轮旋转2°所需要的时间设置为一个时间步长,其值为0.000 336 7 s.当模型泵进出口总压呈现出周期性波动时,认为计算结果收敛,进行下一个旋转周期内数据的时均化处理.

2 性能预测与外特性实验对比

该模型外特性预测曲线与实验曲线的对比图如图4所示.图中K1表示其相对流量,K1=Q/Qd.其中，Q为泵运行实际工况,m3/h；Qd为泵设计工况,m3/h.根据对比图,并考虑到实验过程中存在一定的误差,总体认为扬程、轴功率及效率的数值计算结果与实验结果吻合程度较好,尤其对于设计工况点的预测效果更佳.因此,通过DDES湍流模型在设计工况下可以模拟出与真实内流场近乎一致的结果,对设计工况下一个周期内的模拟结果进行分析,可以探究核主泵水力性能的非定常变化特征.

图4 实验与模拟值的对比Fig.4 Comparison of experimental and simulated values

3 结果分析

3.1 涡结构提取方法

目前已有多位学者提出了多种识别涡结构的方法,Q准则在泵内涡识别方面应用较为广泛,表明其具有较好的适用性[12-15].因此,本文采用Q准则对泵内旋涡结构进行直观地显示,以此来分析一个旋转周期内旋涡结构的非定常演化过程.

根据Q准则的原理,速度梯度张量▽u的特征值应满足以下特征方程：

λ3+Pλ2+Qλ+R=0

(1)

在不可压缩流体流动中,有

式中:λ为式(1)的特征值;S为变形率张量;Ω为涡张量;P、Q、R分别为速度梯度的第一、第二、第三不变量,其值与坐标系无关；Sij=(∂μi/∂χj+∂μj/∂χi)/2；Ωij=(∂μi/∂χj-∂μj/∂χi)/2.

Q方法的提出者认为涡管在Q>0的区域内.从式(3)可以看出,第一项表示流体微元旋转强度的大小,第二项表示流体微元变形强度的大小.Q方法表示以旋涡为主导运动的流体微元处于涡管中,Q值的大小表示旋转强度的大小,Q值为正且较大时,表示流体微元旋转率大于形变率,流体微元处于涡管的中心处.

3.2 一个周期内泵外特性及过流部件损失分析

将叶轮旋转2°所用的时间作为其时间步长.非定常计算时,由于叶轮与导叶在不同时刻具有不同的相对位置,瞬时压力值也在发生变化,所以需要记录叶轮每旋转2°时的一个瞬时压力值.记录叶轮在一个旋转周期内的瞬时数据后,进行计算得到其瞬时外特性值,外特性非定常变化过程如图5所示.图中T1表示相对时间,T1=T′/T.其中,T′表示叶轮旋转60°所用的时间,s；T表示叶轮旋转360°所用的时间,s.

图5 数值模拟结果随时间变化曲线

从图5a可以看出,在一个旋转周期内,扬程没有呈现出明显的周期性,其瞬时变化过程比较明显.在初始阶段,瞬时扬程值总体来说大于平均值；随着叶轮旋转的进行,瞬时扬程值逐渐处于平均值上下,但其变化的脉动幅值均匀性较差,说明核主泵出口压力变化波动不稳定,存在脉动效应.从泵的轴功率变化过程来看,其周期性变化效果明显优于扬程的变化效果,说明在动静干涉作用下,叶轮对液流瞬时做功也具有一定的周期性.对于泵效率而言,在一个周期内总体来看具有周期性,其脉动幅值变化较大.

从图5b和图5c可以看出,叶轮扬程与导叶损失值在一个周期内总体上具有周期性,而压水室损失在一个周期内随机变化程度较大.在一个旋转周期的前1/3阶段内,压水室损失值低于平均值；中间1/3阶段,损失值接近于平均值,在平均值上下进行波动；在后1/3阶段,损失值高于平均值.

从图5b还可以看出,以扬程平均值作为基准线,在一个周期内,瞬时扬程曲线出现30个波峰与30个波谷,在1/6周期内,瞬时扬程曲线出现5个波峰与5个波谷.这是由于该泵叶轮叶片数为6枚,导叶叶片数为10枚,从结构方面来看,两者均为镜像对称结构,在旋转180°的过程中,每枚叶片出口与导叶进口发生5次干涉,3枚叶轮叶片共发生15次干涉,即每12°会发生一次干涉；所以在1/6周期内(叶轮旋转60°)会发生5次干涉,造成瞬时扬程曲线出现5个波峰波谷，在一个周期内会发生30次干涉,从而使瞬时扬程曲线出现30个波峰波谷.对于该泵而言,扬程值在波峰处说明泵内液流瞬时流态较好,叶轮与导叶间的相对位置有利于液流的流动；在波谷处表明叶轮与导叶间的相对位置对液流的流动产生了阻碍作用.

从图5c还可以看出,导叶内的损失明显大于压水室内的损失.这主要是由于液流在叶轮作用下以较高的速度进入导叶流道内,造成了较大的冲击损失,然后液流在导叶流道内降速增压后进入压水室,液流速度相对较低,造成的冲击损失也相对较小.导叶内水力损失呈现出明显的周期性,说明叶轮与导叶间的动静干涉作用影响较大,而压水室与静止导叶相连接,受动静干涉作用影响较小,水力损失受特殊的压水室形状影响而随机性较高.

再结合图6和图7可以看出,一个周期内不同时刻导叶内的涡核分布近似一致,而压水室内不同时刻涡核分布非常紊乱,没有呈现出一定的周期性.因此,泵的瞬时扬程整体上没有呈现出明显周期性的主要原因在于压水室的损失随机波动没有呈现出一定的周期性.压水室损失值随叶轮旋转逐渐在增大,从图7可以看出,旋涡随旋转逐渐在分裂,而分裂的过程中会造成液流能量的损失,从而使损失值增加.

图6 动静叶栅内旋涡结构的演化过程

图7 压水室内旋涡结构的演化过程 Fig.7 The evolution process of vortex structure in pressurized water chamber

总体来看,外特性的周期性变化就是由于叶轮与导叶间的动静干涉作用引起的.叶轮与导叶流道对液流的束缚能力较强,内部旋涡运动具有周期性特征,导致叶轮扬程与导叶损失呈现出一定的周期性.而半球形压水室因特殊的球状结构,其过流断面对液流的束缚能力非常有限,同一截面处液流速度变化较大,旋涡运动没有呈现出周期性特征,造成损失值也没有一定的周期性.

3.3 内流场分析

核主泵动静叶栅在一个旋转周期内不同时刻的旋涡分布如图6所示,过坐标原点截取叶轮回转中心面.图中选取某一叶片固体域部分用黑色标示,可以更加直观地显示不同时刻叶片所处的位置.从图6可以看出,叶轮及导叶流道内分布着不同尺度的旋涡,叶轮内以大尺度带状涡为主,导叶内以小尺度带状涡为主.6个时刻叶轮与导叶流道内旋涡的分布没有明显差别.同时结合图5b可以看出,6个时刻叶轮扬程值大小基本在平均值,说明叶轮相互交替时对应的内流场状态基本一致.

从图6还可以看出,叶轮叶片背面出现一条附着带状涡,此带状涡稳定存在,一直延伸至叶轮出口.在流道中间偏上位置出现另外一条尾迹带状涡,其宽度大于叶片背面的带状涡宽度,该涡会一直延伸至下一叶轮叶片处,在延伸到导叶入口处带状涡会变细,此带状涡几乎占据了整个叶轮流道出口的大部分区域,对叶轮出口液流的顺畅流动产生了较大影响.这主要是由于叶轮工作面与背面的压力不同,叶轮工作面的压力较高,背面压力相对较低,促使液流向背面进行运动,运动过程中液流层之间相互剪切,形成带状旋涡.液流在背面会形成较稳定的带状涡,而在流道中部出现带状涡,说明在流道中部叶轮工作面与背面的压差会进一步发生变化.导叶入口处涡宽度变细,主要是叶轮出口处的高速液流会将其中一部分旋涡冲至导叶流道内,导致尾迹带状涡宽度变细.

导叶流道内,在靠近导叶工作面出现一条带状涡,受液流冲击作用涡核向前逐渐积聚.在导叶背面初始阶段出现一条细长的带状涡,中间位置形成两个小尺度带状涡核,从形状来看,涡核形成是由背面带状涡受液流冲击向前逐渐积聚而成.

核主泵压水室在一个旋转周期内不同时刻的旋涡分布如图7所示，以叶轮回转中心面向进口方向平移300 mm截取平面.由图7可以看出,不同时刻压水室内部旋涡结构随机分布,同图5c压水室损失所反映的结果一致,压水室左侧区域旋涡分布比右侧区域广泛,且强度大于右侧区域.液流运动方向为逆时针,随着旋转的进行,旋涡结构在高压液流冲击下也呈现出逆时针旋转的效果.在压水室出口出现一些旋涡,这部分旋涡可能是由于压水室出口扩散段为环形结构引起的,旋涡结构的非定常变化会引起泵出口压力的波动,造成瞬时扬程出现波动.

3.4 1/6T周期内叶轮外特性分析

叶轮旋转60°过程中扬程、轴功率、效率的瞬时变化过程如图8所示.图中T11表示叶轮旋转60°过程中的相对时间,T11=t/T′.其中,t表示叶轮旋转10°所用的时间,s；T′表示叶轮旋转60°所用的时间,s.从图8可以看出,扬程总体上呈现出周期性,其波动幅度相对较大,波峰处的宽度大于波谷处的宽度,波谷处的扬程值基本一致,而波峰处的扬程值具有随机性,波峰波谷出现的个数与3.2节分析得一致.从轴功率曲线可以看出,其脉动值变化幅度较小,在波峰波谷处的变化趋势与扬程曲线的变化趋势一致.

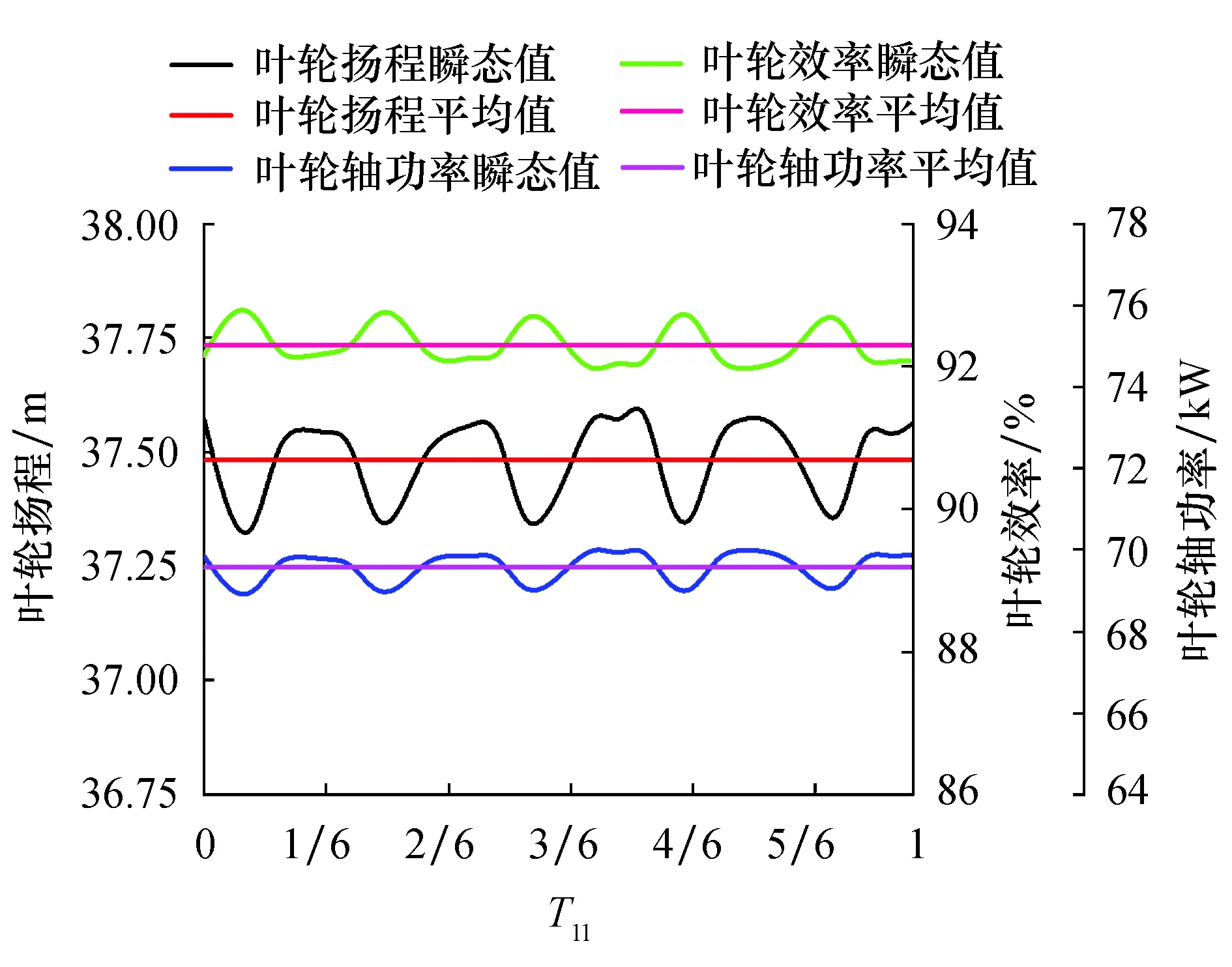
图8 1/6T周期内数值模拟结果随时间变化曲线Fig.8 The variation curve of numerical simulation results with time under 1/6T period

3.5 1/6T周期内内流场分析

叶轮每旋转10°动静叶栅内旋涡发展的演化过程如图9所示.取叶轮每旋转60°进行涡结构的分析，主要是为了观察叶轮相互交替时内部流场的变化特征.因跨度较大,所以进一步减小旋转角度进行分析可以观察叶轮与导叶流道内旋涡结构更细致的演化过程.

从图9可以看出,每旋转10°叶轮内的旋涡结构与每旋转60°叶轮内旋涡结构分布基本一致.1T/6周期内叶轮共旋转60°,即叶轮从A位置运动到B位置.在A位置,叶片出口与导叶入口相对应.在1T′/6时刻,导叶进口处涡带变细,尾迹带状涡中小尺度涡出现脱落并进入导叶流道内.这主要是叶轮出口高速液流冲击涡带,促使其向下游运动进入导叶内.在该过程中,靠近导叶前缘处的涡核一部分进入导叶流道内,一部分被冲击至下一导叶流道内.在2T′/6时刻,导叶进口处尾迹涡明显出现断裂,涡核沿逆时针方向在进行融合.导叶入口处涡b的涡结构变细,流道中间处的涡c向进口延伸,说明受导叶入口液流冲击作用,涡核出现破裂流向下游,与下游涡进行融合.在3T′/6时刻,导叶内涡b进一步向前运动,与下游带状涡c不断逼近,而入口处的带状涡a前端变细,后半段部分几乎没有变化.从2T′/6时刻到3T′/6时刻,在旋转过程中液流对带状涡a前半部分冲击作用明显,造成其前端变细.在4T′/6时刻,导叶入口处带状涡b与下游涡c基本融合在一起,而带状涡a前端出现破裂,与导叶前端稳定的附着涡融合,这两条带状涡融合成一条带状涡.在5T′/6时刻,涡b与涡c已经融合在一起,涡a破裂与背面稳定附着涡进一步相融.总体来看,旋涡结构均会出现融合、分裂的演化过程.

图9 1/6T周期内动静叶栅内旋涡结构的演化过程

从6个不同时刻看涡c,发现其仅在前端部分发生变化,其余部分基本无变化,与背面稳定涡的变化趋势一致.说明在导叶流道前半部分受液流冲击效果明显,然后随着减速扩压,其冲击效果逐渐减弱.

从图8可以看出,在0、1T′/6、2T′/6时刻叶轮瞬时扬程值基本在极大值点,在3T′/6时刻与平均值一致,在4T′/6、5T′/6时刻瞬时扬程值基本在极小值点.

从图9还可以看出,因为涡b由涡a演化而来,涡c在整个周期内变化趋势不明显,所以用涡a的演化过程来分析对瞬时扬程的影响.在0时刻,涡a位于导叶进口处,涡a未发生分裂,其瞬时扬程较高；在1T′/6、2T′/6时刻涡a逐渐出现分裂,靠近导叶进口处,其瞬时扬程稍有下降；在3T′/6时刻涡a已经基本在导叶进口处,但涡a宽度较细,其瞬时扬程值基本与平均值一致；在4T′/6、5T′/6时刻瞬时扬程较低,因涡a结构宽度增大,所以对导叶进口的阻塞程度加剧,造成液流流动受阻.由此可得,导叶进口处不同时刻的涡结构变化会造成不同程度的阻塞,进而导致叶轮瞬态外特性存在脉动效应,加剧泵的振动.

4 结论

通过以上计算与分析,可以得出以下结论：

1) 在一个旋转周期内,由于叶轮与导叶间的动静干涉作用,核主泵瞬态外特性计算值总体上会呈现出一定的周期性,但其脉动幅度的规律随机波动.

2) 叶轮与导叶叶片背面形成的附着带状涡会稳定存在,而在叶轮出口形成的尾迹带状涡在液流冲击作用下会逐渐变细,出现分裂等非定常现象.同时受动静干涉影响,叶轮与导叶流道中的旋涡运动会呈现出周期性特性,而压水室内旋涡运动受特殊的球状结构影响没有呈现出周期性特征,旋涡运动是发展、扩散的变化过程,造成泵瞬时外特性出现波动；

3) 导叶入口处不同时刻旋涡结构的变化会对入口造成不同程度的阻塞,从而影响液流的顺畅流动,导致叶轮瞬态外特性存在脉动效应,加剧泵的振动.