大跨度钢连廊舒适度分析及减振控制

郭宏超， 王凯励， 王德法， 刘云贺， 蔡玉军， 高志宏

(1.西安理工大学 土木建筑工程学院， 陕西 西安 710048； 2.中铁第一勘察设计院集团有限公司， 陕西 西安 710043)

随着我国建筑行业的发展，出现了越来越多的大跨度结构，该类结构通常都有着共同的特点：质量轻、刚度小、阻尼低[1]。尽管结构的静力性能如承载、变形能力可以满足设计和使用要求，但其动力性能，特别是人行荷载激励下的振动效应，很有可能达不到正常使用极限状态的要求。针对结构振动的舒适性问题，我国相关规范尚没有给出详细的设计方法。例如，在《城市人行天桥与人行地道技术规范》[2]中主要根据结构的自振频率来进行控制，即将一阶自振频率控制在3 Hz以上，避开人的步行频率(1.2～2.8 Hz)从而达到控制结构振动的目的。一般对于布置较规则，质量分布均匀的结构，一阶模态振动起主要控制作用[3]。该方法虽然应用简单，但以频率为目标下的结构设计在经济性方面往往造成了较大的浪费。另一方面即使结构自振频率大于3 Hz，当其模态频率与步频的n倍相等时，也有可能引发共振效应，从而不满足舒适性的要求。避开频率法不能将结构正常使用时不同的人行激励强度考虑进来，也不能考虑人所处不同环境时对感受振动的阈值不同。

国内外学者对人行桥的人致振动及其减振方法进行了大量的研究。调谐质量阻尼器(Turned Mass Damper，TMD)作为一个水箱被安装在德国邮政船上，来减少船只的摇晃[4]。随后TMD减振技术在建筑领域得到了实际应用，例如，台北101大厦在87～92层采用了重达660 t的悬吊式调谐质量阻尼器来减小高层结构在风荷载作用下的摆动[5]，减振率最高能达到60%。广州塔在楼中布置有两个重达1 500 t的消防水箱，当摇摆及风力超出正常范围时将启动，水箱可以双向移动来抵消大楼的摆动[6]。Xu和Igusa[7]首次将MTMD(Multiple Turned Mass Dampers)应用于单自由度体系以减少由宽频带随机激励产生的共振，并提出了频率呈线性分布的MTMD思想。此后学者们开始了MTMD理论和应用的研究。李春祥等[8]对MTMD质量、刚度、阻尼比、阻尼系数等参数给出了5种组合方式，基于位移动力放大系数(Displacement Dynamic Amplification Factor，DDMF)和加速度动力放大系数(Acceleration Dynamic Amplification Factor，ADMF)，评估了5种组合下的减振性能差异，得出了刚度和阻尼相同，质量不同时的MTMD组合有更好的鲁棒性，且具有制作方便简单的特点。本文通过考虑某大跨连廊在正常使用中可能出现的各种人行激励荷载，并选择适用于大跨度连廊的各国规范标准对比评价，而后对影响连廊舒适度的几个重要因素进行了参数分析，针对振动过大的问题进行了减振设计。

1 工程概况

某站站房改造项目中的一幢办公及商业配楼，由于规划条件限制，其建筑角部座落在一条地裂缝上，按照有关规程的要求对地裂缝进行有效避让后，结构被分为了3个单体结构，为了保证建筑功能的连续性，使用钢连廊的形式将结构连接起来，见图1。连廊跨度纵向45 m，横向9.5 m，为钢桁架结构形式。在结构高度方向上共设置一个单层桁架和一个双层桁架，其中双层桁架设置标高为14～22 m，单层桁架设置标高为5～10 m。为了减少桁架在地震作用下的受力，支座采用一端铰接一端单向滑动的连接形式，楼板为压型钢板组合楼板。连廊由于跨度大，刚度小，自振频率低等特点，在人行荷载的激励下很容易发生舒适度问题，有必要对其进行详细分析。

图1 大跨度连廊示意图Fig.1 Large-span corridor schematic diagram

2 舒适度评价标准

人对振动的感觉是一个比较复杂的问题，与楼盖振动强度的大小、人所处的环境和人的敏感程度都有关系。国内除了“人行天桥”有频率规定和“高规”[9]有楼盖竖向加速度的规定外，尚无连廊结构的舒适度评价标准，目前国际上关于结构舒适度的有关规定综述见下。

1) 国际标准化组织ISO10137-2007[10]

该标准给出了建筑物及行人通道的舒适度评价指标，认为人可接受的振动水平随运动的频率变化而变化，采用频率计权均方根加速度值r.m.s.(Root-Mean-Square)和振动剂量值VDV(Vibration Dose Value)作为评价标准。

频率计权均方根加速度为：

(1)

式中：aw(t)为瞬时频率计权加速度值，m/s2；T为测量时间长度。标准中提供了频率r.m.s基准曲线，将该曲线乘以与时间、地点、类型相关条件下倍数即得到的舒适度限值。

振动剂量值为：

(2)

频率计权均方根加速度仅适用于峰值比(瞬时计权加速度峰值与r.m.s的比值)小于6的情况，当大于6时，需要采用基于四次方均方根的振动剂量值VDV进行评价，规范中给出了相关限值，可与计算得到的VDV值进行比较，判断结构的舒适性。

2) 美国钢结构设计指南AISC-11[11]

该标准与ISO10137类似，根据提供的基准曲线乘以相应倍数得到不同环境下的限值，但评价指标为峰值加速度，见图2，适用于钢/混凝土结构的人行桥、住宅、办公及商业楼。

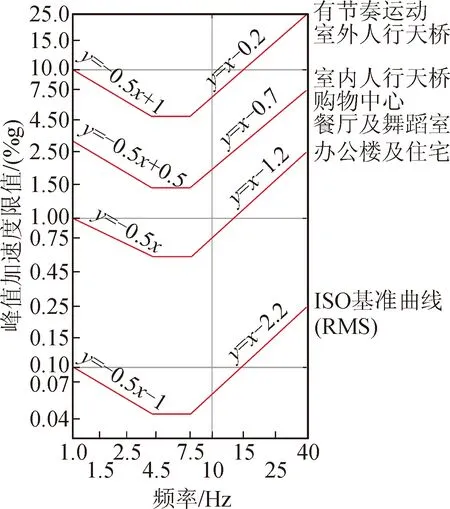
图2 AISC-11舒适度标准Fig.2 AISC-11 comfort criteria

3) 英国钢混凝土桥设计规范BS5400[12]

舒适度评价指标为峰值加速度，限值为alim=0.5(f0)1/2m/s2，适用对象为人行天桥。

4) 欧洲规范Eurocode: Basis of structural de-sign[13]

评价指标采用峰值加速度，限值为竖向0.7 m/s2，水平为0.2 m/s2，特殊人群情况为0.4 m/s2，适用对象为人行桥。

5) 瑞典规范Bro2004[14]

评价指标为均方根加速度r.m.s，限值为0.5 m/s2，适用对象为桥梁。

其他国家如德国虽没有出台相关的规范标准，但也有相应的设计指导手册EN03供工程师参考。就目前来看，以AISC-11为代表的加速度峰值作为评价指标应用时较r.m.s更为简单，再者其振动限值要求相比其他规范考虑了人所处环境这一关键因素。本文应用AISC-11的评价标准，钢结构连廊相当于室内人行天桥，峰值加速度限值为0.15 m/s2，有节奏运动，例如跑动引起的加速度限值为0.45 m/s2。

3 人行激励荷载模拟

1) 单人移动荷载

依据Bachmann[15]的试验结果，人行走时从脚跟着地到脚尖离地过程中对地面典型的作用力曲线见图3(a)。应用时将该荷载作为一个移动的动力荷载，步长为0.85 m，根据步频，以速度v=0.85f0沿结构跨度方向运动。

图3 各工况下荷载时程曲线Fig.3 Time-history curve under various conditions

2) 连续行走荷载

人群连续行走荷载取自国际桥梁协会IABSE(International Association for Bridge and Structural Engineering)[16]中建议的荷载模型：

(3)

式中：t为时间；G为人的体重,取为700N；fs为人的步行频率；αi为动荷载因子，α1=0.4+0.25(fs-2)，α2=α3=0.1；Φi为相位，Φ1=0，Φ2=Φ3=π/2。连廊上有连续通过的人流时，则楼板所受的作用力见图3(b)。

3) 起立荷载

人起立时对楼板的作用力表示为人的体重乘以起立时重心的加速度，见图3(c)。人体重心加速度为：

a(t)=a1sin(2πt/T),t∈[0,T]

(4)

位移为：

s(t)=(T/2π)2a1sin(2πt/T)+C1t+C2

(5)

由边界条件s|t=0=0，s|t=T=h，其中h为人起立时重心升高的高度，v|t=0=0，可以得到：

a1=2πh/T2

(6)

假定起立前后人体重心高度差为0.4 m，起立时间为1s，则a1为2.512 m/s2。

4) 跑动荷载

跑动荷载也取自国际桥梁协会建议的荷载模型，跑动时双脚离地的作用力为零，因此其对地板的作用力为一分段周期正弦半波曲线，见式(7)，典型的荷载时程曲线见图3(d)。

(7)

式中：KP为动力系数；T为一个周期；tP为一个周期内人与地板的接触时间。根据势能条件，一个周期内荷载对时间的积分与重力对时间的积分相等，可以推出KP=T/α，其中α=tP/T为接触时间比。

4 连廊动力特性分析及工况定义

模态分析是一切动力分析的基础，固有频率和振型是承受动力荷载时结构设计的重要参数依据。采用SAP2000 v19有限元软件中的特征向量法进行模态分析，应用杆单元模拟桁架杆件，用同时具有面内和面外刚度的壳单元模拟楼板的真实振动特点，质量源取为恒荷载和20%的活荷载，阻尼比根据AISC-11中室内连廊取为0.01，分析时采用动弹性模量，将混凝土的弹性模量提高1.2倍[17]。

有限元分析得到的基本振型见图4，其中单双层连廊1阶振型均为竖向振动，2、3阶振型为扭转，可见单/双层连廊基频均满足人行桥规范2.5.4条中竖向自振频率不应小于3 Hz的规定，该结果虽避开了人行走的步频范围，但还应进行正常使用状态下的加速度响应分析，应用舒适度标准进行检验。

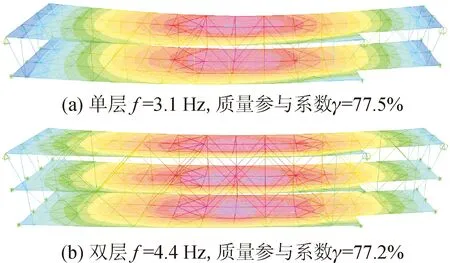
图4 连廊一阶模态云图Fig.4 First mode nephogram of corridor

连廊的建筑功能为人行通道及阅览区，工况定义时考虑结构的实际使用功能，主要为通行荷载。一般来说，行人越多时，对楼面的作用力越大，造成的振动响应越大[18]。但有学者指出，人群通过时，由于每个人对楼面的激励位置不同，引起的振动响应一定程度上会相互抵消而不一定总比单人通过时大，所以此处同时考虑单人与人群两种工况。当人群通过时，所有人都保持同步调相位行走的情况一般不可能发生，应考虑人群折减系数，根据德国人行桥规范EN03[13]提出的等效人数的计算公式，见式(8)。将计算出的等效人群荷载均布于楼面上以考虑人群作用。工况定义见表1。

表1 人行激励分析工况Tab.1 Pedestrian excitation analysis conditions

(8)

式中：N为行人数量；ζ为结构阻尼比；Ne为人群密度。

表2 各行人密度下行走特点Tab.2 Walking characteristics of different pedestriandensities

5 舒适度分析结果

1) 单人通过工况的分析结果

工况1、2下，行人行至连廊跨中时，加速度响应达到最大值，单层连廊为0.14 m/s2，双层连廊为0.074 m/s2，行人脚步作为一节点形式的集中荷载，对结构的激励不均匀，没有出现典型的共振现象，满足舒适度要求，其中单层连廊两工况下的加速度时程曲线见图5(a)和(b)。

2) 连续人群通过工况的分析结果

连续人群慢速通过时，单双层连廊均存在明显的共振现象，单层加速度响应为0.42 m/s2，双层为0.147 m/s2，提取单层连廊的加速度时程和频谱曲线见图5(c)和(d)。从频谱曲线来看，在1阶和2阶自振频率处加速度响应存在峰值，说明人群慢速通过时步频1.55 Hz的2阶倍频3.1 Hz与结构的基频3.1 Hz发生共振效应导致加速度逐步增大。而快速通过时，2.8 Hz的步频由于偏离两结构基频，造成的加速度响应较小，满足限值要求。

3) 其他工况的分析结果

随机人群通过时，每个行人的步频相位均不相同，且其主要步频1.87 Hz及其及倍频与结构基频相距较远，没有共振现象，加速度响应为所有工况中最小。连廊座椅处所有人集体起立时对结构的脉冲作用引起的加速度响应也满足舒适度要求。跑动时，由于其动荷载因子较大，对楼板作用力相比于步行时要大，引起的加速度响应最大，单层连廊达1.28 m/s2，存在舒适性问题。各工况下结构峰值加速度响应见表3。

6 舒适度影响因素分析

6.1 楼板厚度的影响

结构中楼板作为人致荷载的直接作用面，其厚度直接影响楼板的刚度。为了研究板厚度对结构振动特性的影响规律，分别选取80 mm到180 mm厚的楼板进行分析，人行荷载取连续人群荷载，步频取为基频的1/2，其对结构自振频率及加速度的影响见图6。由图6可发现，在板厚逐渐大的过程中，其基频变化从3.09 Hz升到3.12 Hz，二阶频率变化从4.89 Hz升至4.98 Hz，频率变化较小，而挠度从42.5 mm降至38.5 mm，变化较大，说明板厚增加可以较为显著增加整体结构刚度，由于频率与结构的刚度和质量分布有关，刚度变化的同时，质量也增大，频率的变化不明显。从图6中还可以发现，随着板厚度的增加，结构跨中加速度近似呈线性减小，说明增大板厚能抑制结构的竖向加速度，但对于此大跨度结构来说，效果依旧不能满足舒适性要求。

图6 结构自振频率及加速度响应与板厚的关系曲线Fig.6 Relationshipbetween structure vibration frequency and acceleration vs thickness of slab

6.2 楼板边界条件的影响

边界条件也是影响楼板刚度因素之一，一般分为固支与简支，在均布人群荷载下对比固支与简支两种情况下楼板的加速度响应情况见图7。固定的边界条件下，峰值加速度为0.41 m/s2，简支的峰值加速度为0.39 m/s2，从云图可以看出，最大加速度响应位置和峰值基本一致，都是从四周向中间逐步增大。说明楼板边界条件的变化对结构整体刚度影响较小，对舒适性影响不大。

图7 不同边界条件下楼板加速度云图Fig.7 Floor acceleration nephogram under different boundary conditions

综上所述，楼板厚度与边界条件是刚度的影响因素。对于大跨度钢桁架式连廊这种结构来说，在结构形式无法改变的情况下，应首先考虑采取增加板厚的方式来改善舒适性。

6.3 人对结构振动特性的影响

有研究表明，结构上留驻的人群会对结构的动力特性产生影响，国外许多学者都曾通过试验指出，由于留驻人群的作用，结构的阻尼明显增大。后来，Brownjohn和Zheng[17]在进行更深入的研究后发现，楼板上的人群在振动过程中吸收的能量明显大于混凝土楼板。

研究人对于结构振动特性的影响，需要选择一个合适的人体生物动力学参数，Coermann[20]最早于1962年进行了人体动力特性测量试验，得出人体的频率为5.0 Hz，阻尼比为32%的结论，后来Brownjohn[21]等进行过多次试验，也得出了近似的结论。本文选用的ISO-5982[22]标准中总结了各学者的研究成果，给出对于站立的人，阻尼比为37%，频率为5.0 Hz，由频率和阻尼比则可以计算出人的刚度、阻尼系数。

在实际结构中，行人通常是无规则分布于楼面上，若采用这种精细的建模方法工作量巨大且不容易实现。因此考虑一种简化方法，将人群视为按一定密度分布在连廊的不同位置上的数组人组成，利用共振放大法计算结构的阻尼比，该方法使激振频率与结构固有频率相等以产生共振响应，通过捕捉静位移和共振时的位移两个参数即可计算出结构的阻尼比，结果见表4。由表4可知人群会显著增大结构的阻尼，不同的行人建模方式得到的结构阻尼比差别很小，最大相差2%，表明将行人以组的形式施加相比于精确建模可以避免大量重复工作且可以得到较为精确的结果。

表4 人群不同模拟方法下结构的阻尼比Tab.4 Damping ratio of structure by people’sdifferent simulation methods

将行人模型应用于单层连廊结构，根据前述步频与人群密度的关系，步频为1.55 Hz时，人群密度为1.5人/m2，将行人分组建模，每块楼板上的人群为一组，进行人群连续通过时的加速度响应分析，所得到的结果见图8。由图8可知，考虑人效应后，结构加速度响应有所降低，人群密度为1.5时，降低约30%，人群密度为0.1时，降低约6%。说明人的质量比越大，其对结构的阻尼作用增加越明显，加速度响应越小。

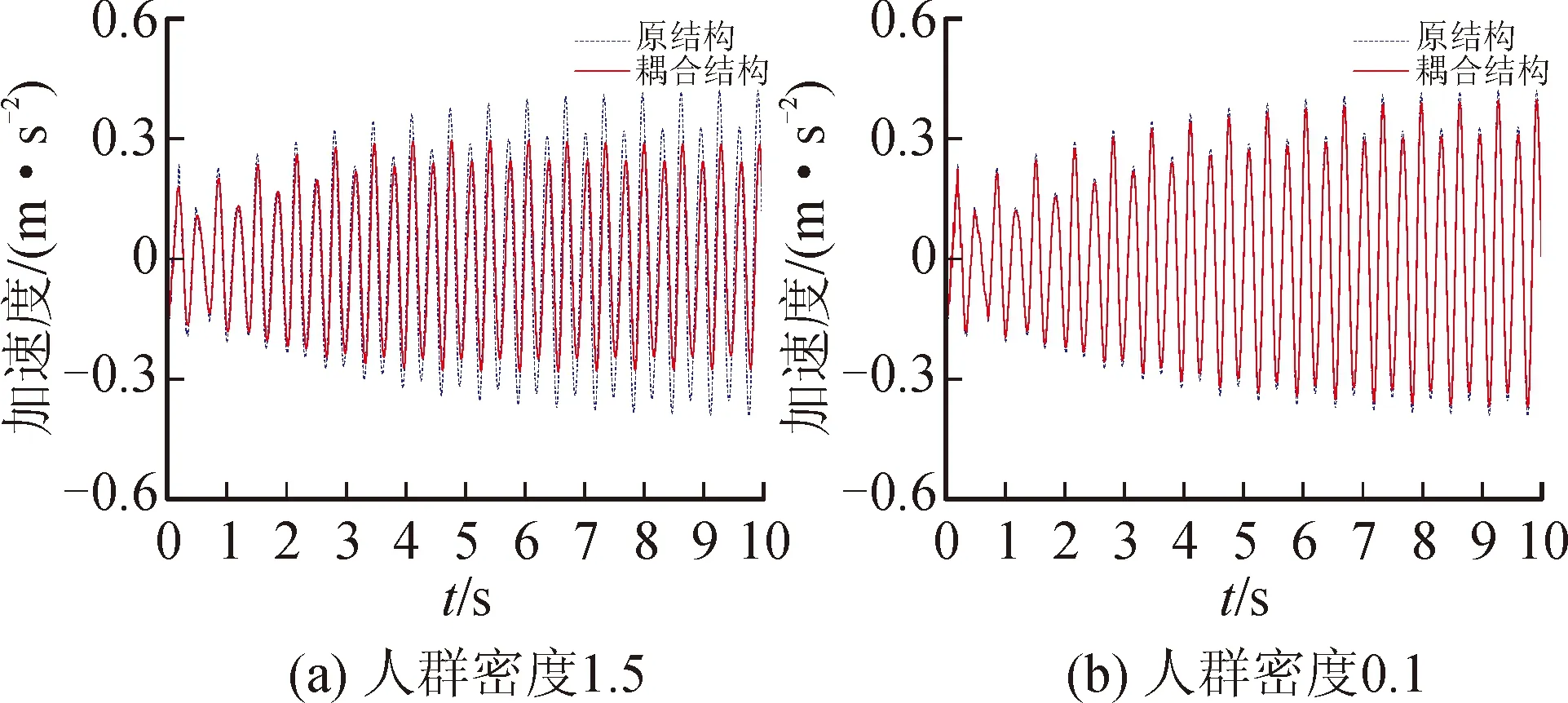
图8 考虑人作用后结构加速度响应时程曲线Fig.8 Time-history curve for structural acceleration response considering human structure interaction

综上，人群的存在会影响结构的动力特性，其阻尼效应能够吸收部分振动能量，降低结构的振动响应，通常在进行舒适度分析时并不考虑人与结构的相互作用效应，得到的计算结果会偏于保守。

7 减振系统原理及设计

根据前述舒适性分析结果，单层连廊由于其自振频率较低，在人群通过时存在舒适性问题，需对此进行减振控制。目前对于人致振动的控制主要使用被动控制装置调谐质量阻尼器(TMD)。

TMD主要由质量块-弹簧-阻尼器组成，其工作原理是将原结构的振动通过弹簧转移至质量块，利用阻尼器消耗振动的能量[23]。

见图9，选择一个质量比μ和频率比f，可以画出不同阻尼比时主结构动力放大系数与频率之间的关系曲线，见图10，表明良好的减振效果取决于减振系统的参数选取。根据此原理，Den Hartog[24]通过推导得出了TMD系统的最优参数。

图9 连廊-TMD系统Fig.9 Corridor-TMD system

图10 动力放大系数曲线Fig.10 Dynamic magnification factor curve

最优频率比为：

(9)

最优阻尼比为：

(10)

值得注意的是，Den Hartog[24]推导的最优参数解析式是以最小位移为目标且主结构阻尼为零或非常小。一般来说，当主结构存在阻尼时此公式具有一定的误差，但对于大跨度钢桁架这种小阻尼柔性结构来说，该误差非常小。Bachmann[17]指出，式(6)～(7)在适用于主体结构阻尼比ζs≤0.02的小阻尼情况时，可以达到较为理想的减振效果。

单层连廊主结构频率f=3.1 Hz，1阶振型竖向参与质量为452 t。根据最优参数计算公式，分别取质量块为300 kg、500 kg、700 kg，各质量比下TMD参数见表5，在上下弦振动响应最大位置处各布置一个，计算结构在不同质量比TMD下对人致振动的减振效果。结果表明，TMD系统质量比越大减振效果越好，在质量比为0.22%(500 kg)时，加速度即可满足舒适度限值要求，为0.148 m/s2，减振率为64%，见图11(a)。从图11(b)加速度频幅曲线也可以看出，在布置TMD后，3.1 Hz处的加速度峰值急剧减小，但在2.95 Hz和3.25 Hz处的响应值出现增大现象。在不增加质量比的情况下，人群以该两点处的频率通过时的加速度响应将不满足舒适度限值要求，因此需要扩大减振频带的宽度。

表5 各质量比下TMD参数Tab.5 TMD parameters for various mass ratio

图11 减振结构加速度时程和频谱曲线Fig.11 Acceleration time history and frequency curve for vibration damping structure

Xu等[7]提出了参数计算方法，通过使质量、刚度、阻尼、阻尼比等四个参数中的两个为常量、改变其他两个变量使MTMD系统的频率呈线性分布来达到扩大减振频带宽度的目的。其中，使每个减振装置的刚度和阻尼相同，质量和阻尼比不同的方案制作简单高效，其参数计算公式为：

(11)

MTMD系统的中心频率设为3.1 Hz，经过多次循环优化计算，最终减振装置个数取为每组3套，上下弦各布置1组，其总质量比为0.64%，平均阻尼比为0.02，调谐频率范围为2.95～3.25 Hz，则每套TMD设计参数见表6，布置位置见图12。

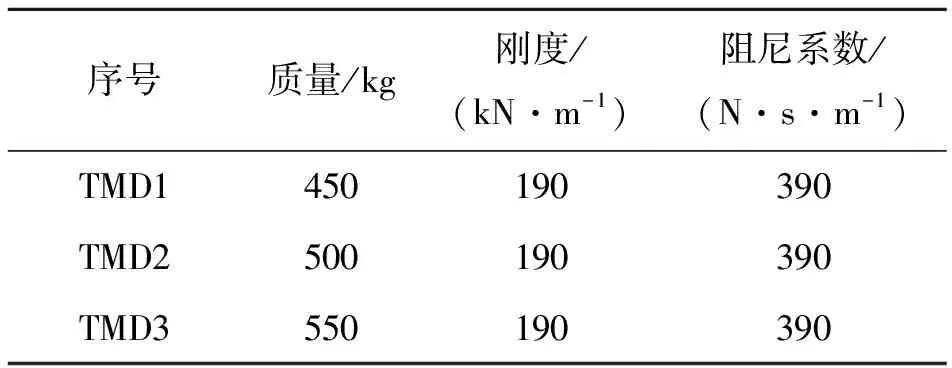
表6 MTMD参数Tab.6 MTMD parameters

图12 TMD布置位置示意图Fig.12 TMD position schematic diagram

对布置TMD的大跨连廊结构进行加速度响应分析，见图13。结果显示多频率减振系统在调谐中心频率3.1 Hz处的加速度响应为0.125 m/s2，相比于单频率提高了15%，原因为调谐其它两频率点处的减振装置也对中心频率处的振动有一定的抑制作用。从频幅曲线可以看出在中心频率周围没有出现像单频率减振系统那样加速度突然增大的现象，表明MTMD系统扩大了减振频带的宽度，更具有鲁棒性。

图13 减振结构加速度时程和频谱曲线Fig.13 Acceleration time history and frequency curve for vibration damping structure

8 结 论

通过对此连体结构中大跨度连廊的舒适度及TMD减振控制分析，可以得到以下主要结论。

1) 大跨度结构具有刚度小，质量轻、阻尼小等特点，舒适性问题除了频率控制标准外还应考虑与人感受直接相关的不同环境下的加速度限值要求，使用与结构使用情况相同的多工况进行分析。

2) 在结构形式不变的情况下增加楼板厚度能有效地降低大跨度桁架的振动加速度。人的阻尼特性在振动时可以吸收部分能量，最大人群密度下能使加速度降低约30%，在舒适度分析时，不考虑人作用的计算结果偏于保守。

3) 调谐质量阻尼器作为被动减振装置可以有效降低结构的人致振动加速度，改善结构的舒适性能。TMD质量比越大减振效果越好，当质量比为0.22%时，减振效率可达64%。采用多频率TMD可以获得更大的减振的频带宽度，在激励频率偏离时使其更具有鲁棒性，且调谐其它频率的减振装置对抑制中心频率处的振动有一定的贡献，当质量比为0.64%时，可以使减振率进一步提高15%。