PCD算法对音频信号降噪的参数选择
何选森, 徐 丽, 樊跃平
(1.广州商学院 信息技术与工程学院, 广东 广州 511363; 2.湖南大学 信息科学与工程学院, 湖南 长沙 410082)
降噪是信号处理最重要的任务之一,而对信号的分解有助于降噪。利用字典可以将信号分解成一系列原子的线性组合[1]。以超完备字典[2]为基础,冗余(稀疏)表示提供了一种强有力的信号模型[3],它将信号近似为超完备字典中最少数量非零原子的线性组合[4]。信号的稀疏表示具有潜在的降噪能力[5],以冗余表示为基础的收缩[6]成为具有吸引力的降噪技术。小波收缩[7]使用正交变换实现降噪,而新的趋势则是采用超完备变换。在众多信号分解方法中,基本追踪(basis pursuit, BP)[8]法是将信号分解为字典原子的最佳叠加,并使表示系数的l1范数(或l0范数)最小化[9]。对于消除Gauss白噪声,基本追踪降噪(BP denoising, BPDN)[10]是最佳的。基于超完备字典和冗余表示,迭代收缩(iterative shrinkage, IS)算法[11]成为一种高效的数值技术。文献[12]提出了四种IS算法,其中并行坐标下降(parallel coordinate descent, PCD)法具有最快的搜索速度。文献[13]对PCD进行了收敛性分析,并引入正则化函数的形式,使得对坐标优化提供解析的解。PCD在图像处理[14]和图像降噪[15]方面获得了广泛的应用。
尽管PCD被证明是一种优秀的图像降噪算法,但它在音频降噪领域并没有得到相应的运用。这是因为在音频或语音信号降噪时,需要事先对PCD算法的参数进行设定,而目前还没有文献给出相关参数的设置标准。正是基于这种考虑,本文利用仿真实验,研究PCD算法相关参数的选择依据。主要通过比较音频信号外加Gauss噪声的强度、软收缩函数的阈值、算法的迭代次数、分解信号的超完备字典与PCD降噪性能之间的关系,给出以上参数选择的基本原则,以扩展PCD算法的应用范围。
1 去噪背景
设x∈RN为N维观测信号矢量,s∈RN为信源,T∈RN×N为正交变换,则观测信号表示为x=Ts。对于稀疏信源s,在同一时刻,只有很少分量si∈s是非零值,其它多数分量都为零值。在实际应用中,信源是不可观测的,只能通过传感器采集来获得观测信号x。由于采集信道噪声的存在,x中不可避免地包含了噪声。对于稀疏信号,小波分析中的收缩降噪方法[16]是假定绝对值很小的分量为噪声并将其设置为零,而仅保留较大绝对值的分量以实现降噪目的。
若信号x∈RN可以由几个(单位能量的)原子dk的线性组合来近似,则由所有原子组成的集合{dk:k=1, 2, …,K}就是一个字典D∈RN×K。设矢量z∈RK是稀疏的,则x可表示为:
x=Dz
(1)
式中:z是信号x的重构系数。
当K=N时,字典D是正交的,则式(1)的表示是唯一的。当K>N时,字典D是超完备的,这种情况下式(1)存在有无限多个可能的系数集。这种非唯一性表示提供了极大的选择性,即从众多表示中选择最适合的表示。寻找具有最少量非零系数的解是一种非常具有吸引力的优化技术[17]。当使用超完备字典分解信号时,式(1)给出了欠定的线性方程组,它的最稀疏解可表示为如下的优化问题[17]:
(2)
或者
(3)
式中:ε是误差容限;‖⋅‖p为lp范数;l0范数是对一个向量非零元素的计数。
式(2)~(3)中的优化问题可以通过正交匹配追踪法[12]求解。基本追踪(BP)是寻找系数具有最小l1范数的信号表示[9],若在式(2)中用l1范数代替l0范数,则有:
(4)
式中:l1范数是求向量各元素绝对值的和。
因l1范数是l0范数的凸化[17],也就是说式(4)是式(2)的凸化。为了更接近于实际应用的环境,考虑一个含噪声的信号矢量
y=x+v
(5)
式中:y∈RN是信号x的含噪声观测量;v∈RN是Gauss零均值白噪声向量,并且限制它的能量为有限值。对信号y降噪的优化问题表示为[18-19]:
(6)
此问题可以由Lagrange形式替代[9]:
(7)

2 超完备字典
在PCD算法中,超完备字典起着非常重要的作用,选择合适的超完备字典是PCD实现收缩降噪的前提条件。
在音频信号处理领域,有两种典型的超完备字典,分别是离散余弦变换(discrete cosine transform, DCT)字典[20]和Gabor字典[20]。
一个窗口式DCT字典表示为DDCT=[d1,d2, …,dK],它的第k个原子定义为[20]
(8)
式中:1≤k≤K;0≤t≤N-1;N是每个音频帧的长度;K是DCT字典的大小(尺寸),也就是离散频率的数量;wd是加权窗口。
DCT原子通过引入初始相位φ可推广为Gabor原子,这样做是为了增强信号结构的潜在适应性和信号的稀疏性。
窗口式Gabor字典表示为DG=[d(k,φ)](k,φ)∈Ψ,原子以连续参数集Ψ=[1,K]×[0, 2π]为索引,定义为[20]:
(9)
式中:1≤k≤K;0≤t≤N-1;N是帧的长度;K是Gabor字典的尺寸大小;φ是它的相位;wd是其加权窗口。在无任何近似的情况下,Gabor字典连续索引的原子d(k,φ)的分解可以用离散字典中的原子对来表示。一对的原子可以是相同频率且相位为零的余弦和正弦对:
(10)
(11)
一般地,对DCT和Gabor词典的列向量(音频帧)都进行归一化处理以简化其计算。例如式(10)~(11)所示Gabor字典的正弦和余弦原子,采用它们对应的单位范数版本。
3 PCD算法
实际上,式(7)就是PCD算法的目标函数[12]。对于含噪声信号y,去除其中的Gauss噪声可归纳为对以下函数的最小化[12]:
(12)
当采用最大后验概率估计时,函数f(x)可从Bayes的观点来解释。在式(12)中,等号右边第一项通常被称为对数似然,它描述干净信号x与其含噪声观测量y之间的关系,而第二项ρ(x)表示未知信号x的先验值。对不同的函数ρ(x),式(12)中f(x)具有不同的展开式。如果字典D是超完备的,则式(12)的目标函数将变成以下的优化问题[12]:
(13)
将优化式(13)与式(7)比较可知,在PCD算法中,函数ρ(z)采用的是l1范数。在文献[12]中详细地介绍了PCD算法的推导过程,这里仅给出最终的更新迭代式:
zk+1=zk+μ{S[v(D,y,zk)]-zk}=zk+μhk
(14)
式中:hk是可计算的向量;zk是z的第k次解,zk+1是其更新值;μ是步长参数,若μ=1,则采用完全收缩,若μ<1,则效果为松弛步长;S是软收缩(阈值)函数,其定义为:
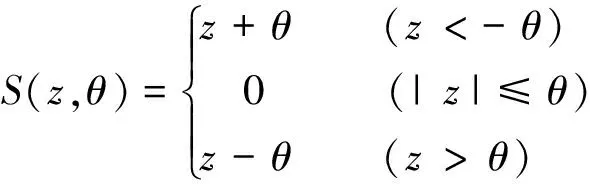
(15)
式中:θ为阈值。
在式(14)中,向量v(D,y,zk)定义为:
v(D,y,zk)=diag-1(DTD)DT(y-Dzk)+zk
(16)
由式(14)可知收缩函数S以阈值λ⋅diag-1(DTD)·1K对向量v(D,y,zk)逐项操作,其中1K表示元素为1的K×1矩阵(列向量)。由于字典D的列是归一化的,则diag-1(DTD)=I,其中I为单位矩阵。于是,式(16)可简化为:
v(D,y,zk)=DT(y-Dzk)+zk
(17)
PCD算法的搜索速度可以通过线搜索[11]或序列子空间优化[19]来进一步加快。线搜索即一维搜索,是指单变量函数的优化过程。在PCD算法中,线搜索用于寻找最佳的步长μ,其目的是求解以下的优化问题:
(18)
而式(18)的解是通过求下面的方程获得:
(19)
式中:sign为符号函数。式(15)也具有收缩的结构。

4 仿真结果与分析
4.1 仿真环境与性能指标
为了验证PCD算法对音频信号的降噪性能,通过一系列仿真实验,归纳出算法相关参数的选择原则。仿真PC机配置为:Intel(R) Celeron(R) 1007U-1.5 GHz的CPU,4 GB内存,Windows 10操作系统。所有仿真都是在MATLAB 9 (R2016a)上运行。用于测试的音频源信号为两通道的音乐信号,其类型为wav,信号的采样率为44.1MHz。每个信源样本数为L=216=65 536。五个音频信源X=[x1,x2,x3,x4,x5]T的时域波形见图1。

图1 五路音乐音频源信号的波形Fig.1 The time domain waveform of 5 source signals
为了测度PCD算法的降噪性能,采用两种经典的技术指标,分别是信噪比(signal to noise ratio, SNR)和均方根误差(root mean square error, RMSE):
(20)
(21)

信号降噪的仿真过程如下。在时域中音频信源与Gauss噪声相加生成含噪声的观测信号。每个观测信号乘以长度为64的Hamming窗以生成音频(语音)帧,使连续两帧之间的重叠样本数为32,即每一帧的前后各有16个样本与相邻帧的样本重叠。音频帧的分割过程是通过使用Voicebox中的MATLAB函数enframe来实现。将PCD算法应用于分帧后的观测信号进行降噪,每次使用PCD是对一帧进行处理。对每个降噪的帧乘以逆Hamming窗,且在相邻帧重叠的样本中,分别在每一帧两边各去除50%的样本,仅保留每一帧中间部分的样本,最后将经过处理的各个片段简单串联起来即可得到重新合成的降噪后的信号。
PCD算法的迭代过程如下。设定最大迭代次数M。将迭代次数初始化为k=1,仿真开始。在PCD算法每次迭代后计算并记录相应的RMSE和SNR值。然后,将迭代次数更新为k←k+1,以重复执行PCD算法。最后,判断仿真过程是否结束,若k 在PCD算法的迭代中,需要预先给出软收缩函数S的阈值λ。在确定最优的阈值λ时,可以使用全局阈值规则和最小最大阈值规则[7]。本文采用全局阈值规则,其λ的取值范围为[7]: (22) 式中:L是信号的样本长度;σ是Gauss噪声的标准差。从式(22)可知,要确定阈值λ,就必须先要给出噪声的强度σ。 音频信源在被加入Gauss噪声后生成观测信号, 而加入的噪声强度采用(input)信噪比来度量。为确定噪声强度对降噪性能的影响,本小节采用小波软阈值降噪法。小波的类型为db45,当观测信号的输入(input)SNR=10, 15, 20dB时,利用小波降噪获得相应的输出SNR值和RMSE值。在这个仿真中,对于五个信源的加噪、降噪过程重复进行了100次实验。在每次实验后,分别计算并记录全部五个观测信号在一次实验中平均的输出SNR和RMSE值。仿真实验的结果见图2。 图2 五个信号的平均输出SNR和RMSE值Fig.2 Average output SNR and RMSE of five signals 从图2的平均性能指标可以看出,随着观测信号中SNR值的降低(即噪声强度增大),小波软阈值方法的降噪性能变差。特别地,当(input)SNR=10时,降噪后输出的平均SNR<9.8,即经过降噪处理的信噪比小于降噪前的信噪比。这说明由于噪声强度过大,信号被严重污染而不能恢复。对音频信号来说,(input)SNR=10是一个非常恶劣的环境。 为便于分析和比较,对每一个输入的SNR值,分别计算施加到每个信源上的噪声强度σ。其对应的结果见表1。 表1 输入SNR与噪声强度σ的对应关系Tab.1 Correspondence between input SNR andnoise intensity 从表1的数据可以看出,对于相同的输入SNR值,不同信源被施加的噪声强度是不相同的,这是因为每个信源的幅度(或功率)都不相同所致。对于(input)SNR=10的最坏情况,施加到信号x2,x3,x4,x5上的噪声强度接近0.1,而施加到信号x1的噪声强度为0.2。为统一起见,在下面的仿真实验中,将相同的噪声强度(σ=0.1)施加于五个信源形成含噪声的观测信号,也就是PCD算法的输入信号。 在给定噪声强度σ之后,利用式(22)就可以求出软收缩函数S的阈值λ。 因为信号的采样点数为:L=216=65 536,因此有(2log2L)1/2=4.7096,从文献[7]中的Table 2可以知道,在给定σ=1时,其参考的阈值为λ*=3.310。由于本文中选取σ=0.1,将它代入到式(22)可得结果:λ≤σ×3.310=0.331 0,显然这只是λ的一个取值范围。为了找出PCD算法的最佳阈值λ,通过以下的仿真实验来进行确定。其实验条件为:每个观测信号都被分割成长度为64的音频帧,设置PCD算法的最大迭代次数为M=5。软阈值λ的值从0.05到0.331 0不断地变化,其更新步长为0.01。超完备字典分别采用DCT和Gabor,对每个λ值和每个字典仅进行一次实验。图3给出了在这种条件下PCD算法输出的SNR和RMSE值。 图3 五个信号对不同λ值的输出SNR和RMSEFig.3 Output SNR and RMSE of five signals for different λ’s 从图3的结果可以看出,无论采用DCT还是Gabor字典,PCD算法对每个观测信号的降噪性能,即输出的SNR和RMSE值随着阈值λ的增加都有明确的变化趋势。显然地,当λ=0.1时每个信号的输出SNR达到相应的最大值,而每个信号的输出RMSE也达到相对应的最小值。这说明当选取阈值λ=0.1时,PCD算法能获得最好的降噪效果。 从图3还可看出,对于不同的超完备字典,PCD算法的去噪性能是不相同的。因此,在给定噪声强度σ和软收缩函数的阈值λ之后,还需要分析超完备字典对PCD算法降噪性能的影响,以确定最适合于PCD算法的字典。 在这个仿真中,PCD算法的最大迭代次数设置为M=15。分别采用DCT和Gabor字典,对每个观测信号利用PCD算法进行降噪处理,并计算和记录每个信号在每次迭代中的性能指标。图4给出了实验的结果(输出的SNR和RMSE值)。 图4 五个信号对不同字典的输出SNR和RMSEFig.4 Output SNR and RMSE of five signals for different dictionaries 从图4的输出指标波形可以看出,随着迭代次数的增加,PCD算法的降噪性能逐渐得到提高,即PCD算法随着迭代次数的增加而逐渐收敛。观察第一个信号(即signal1)的波形可知,使用Gabor字典所得到的SNR值要大于使用DCT字典对应的SNR值。同样地,使用Gabor字典得到的RMSE值要小于使用DCT字典的RMSE值。此外,信号2至信号5输出的SNR和RMSE值也都具有相类似的关系。这意味着使用Gabor字典,PCD算法可以获得更好的降噪性能。 在给定噪声强度σ,软阈值λ,并采用Gabor超完备字典的情况下,研究PCD算法的降噪性能与算法迭代次数的关系。在这个仿真中,PCD算法的最大迭代次数设为M=50,Gabor字典的尺寸为N×K=64×1 024,它的加权窗口wd为长度N=64的对称正弦窗口。在PCD算法的每次迭代过程中,分别记录每个信号的输出SNR和RMSE值,其结果见图5。 图5 五个信号在每次迭代后的输出SNR和RMSEFig.5 Output SNR and RMSE of five signals after every iteration 从图5的输出结果可以看出,对于每一个观测信号,在经过大约25次迭代后,PCD算法降噪的指标SNR和RMSE值达到相对应的稳定值。也就是说,以降噪为目标的PCD算法,其收敛条件为算法需要经过25次的优化迭代。 针对音频信号的降噪问题,本文通过仿真,比较分析了算法的相关参数对PCD降噪性能的影响。仿真结果表明如下结论。 1) Gauss白噪声的标准差为0.1(或输入的SNR=10)时会造成小波降噪性能的严重下降,这是因为音频信号本身的幅度(功率)较小所致,此结论对音频信号处理具有指导性意义。 2) 当软收缩函数的阈值为0.1、采用Gabor字典时PCD算法能取得很好的降噪性能。 3) 当迭代次数为25时,PCD算法能获得稳定的收敛。4.2 噪声强度对降噪性能的影响


4.3 软阈值对降噪性能的影响
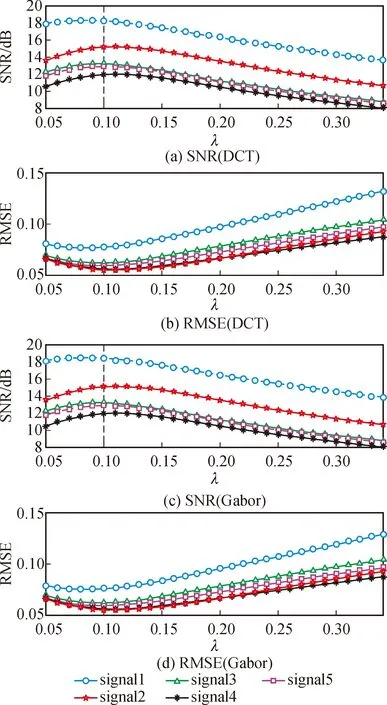
4.4 超完备字典对降噪性能的影响

4.5 算法迭代次数对降噪性能的影响

5 结 语

