吸附热对煤-气相互作用的数值模拟研究

李曜辰，王春光

(山东科技大学 能源与矿业工程学院,山东 青岛 266590)

0 引 言

煤层气开采与矿井瓦斯抽采均涉及多物理耦和过程。煤层气的主要成分是甲烷，大部分甲烷以吸附状态存储在煤孔隙/裂隙结构中。当煤储层压力降低后，吸附态甲烷分子会解吸成游离态，从煤基质内扩散进入裂隙。在此过程中，会出现煤基质收缩，煤裂隙压缩导致渗透率变化，进而又会影响后续的吸附气体解吸-扩散-渗流。因此研究煤-气吸附/解吸过程对煤储层物性的动态影响规律是高效开发煤层气、提高煤层气抽采量的基本科学问题[1]。

有关煤储层流-固耦合关系已经开展大量的研究[2-6]。张宏斌等[7]根据有效应力原理建立的单孔隙渗透率模型，得到了业内广泛应用[8-9]。考虑到深部煤储层温度较高，曲鸿雁等[10]从热力学的角度将温度变量引入Langmuir吸附方程,建立了吸附参数与环境温度的数学关系。李宝林等[11]研究了煤层温度对气体渗流的影响。XIA等[12-13]考虑了焦耳汤姆逊效应对温度的改变，构建了热-流-固三场耦合的模型。XUE[14]考虑了非达西流体和滑脱效应对温度的影响。KHALILI[15]建立了双孔弹性介质的非等温流动和变形的偏微分方考虑了热对流、温度梯度和压力梯度引起的流体通量、相压收缩热等。这些研究表达了热流固耦合过程，揭示了温度、固体、气体互相作用演化的机理。

煤的吸附能力与其孔隙结构发育和矿物组成有关[16]，不同煤阶的吸附性能差异显著[17]。目前评价煤对气体的吸附参数多数是进行等温吸附实验，根据Langmuir[18-19]或Brunauer-Emmett-Teller(BET)[20]等温吸附方程确定相关参数。值得注意的是，在吸附过程中气体分子移向固体表面，其分子运动速度降低同时释放出热量；而在解吸过程中，气体分子需要吸收热量才能脱离固相表面。发生在煤粒表面甲烷或二氧化碳的吸附过程属于物理吸附。YUE等[21]观测到了气体吸附使煤粉温度升高的现象[22]。刘志祥等[23-24]、孟召平等[25]和CHABANK等[26]讨论了吸附热产生的机理，研究了宏观温度变化与微观分子吸附解吸等行为之间的关系。为研究温度对吸附的影响，周胜国等比较了不同吸附方程的准确度，测量了不同温度下吸附参数，研究了不同温度与压力组合条件下平衡吸附量，建立了吸附参数与温度的对应关系[27]。

由此可见，现有的基于等温吸附试验得到吸附量与压力关系描述了温度与压力均处于平衡状态下固体颗粒吸附气体能力。然而，等温吸附过程未能考虑气体动态吸附产热对孔隙结构的影响。吸附热是注采过程中一个并没有得到足够重视的影响因素。通过对改变温度，影响温度敏感因素，从而对煤-气相互作用过程产生影响，吸附热在煤中气体的注采过程中扮演了重要角色。

基于此，根据双孔隙介质理论，在固体变形-气体流动-吸附解吸耦合关系中引入吸附热。其中，温度与吸附的相互影响，温度与固体变形、气体流动的相互影响将控制整个物理过程。将煤的吸附应变值定义为温度函数，煤-气系统的储热项划分为裂隙系统与基质系统；并以固体应变作为耦合项，考虑了煤与环境热交换过程，建立考虑吸附热的“变形-渗流-扩散”耦合计算模型。探究煤在吸附解吸气体时温度的变化规律，为煤层气开采时煤层温度演化提供参考。

1 数学模型

1.1 煤体变形方程

煤体的力学平衡方程定义为

σij,i+fi=0

(1)

其中：σij,i为应力张量的分量，fi为体力的分量。煤体弹性阶段的几何变形方程可以表示为

(2)

其中：εij为应变张量，ui,j和uj，i为位移张量。

根据煤的双重孔隙结构，煤体的本构关系包括：弹性变形、气体吸附、热膨胀及裂隙系统与基质系统间压差影响(图1)其与应变的数学关系可以分别表示为

图1 裂隙-基质结构示意[28]

(3)

(4)

其中：εmij、εfij分别为基质应变与裂隙应变；σij为应力；基质切变模量Gm=Em/2(1+νm)，裂隙切变模量Gf=Ef/2(1+νf)，νm、νf分别为基质泊松比与裂隙泊松比；基质体积模量Km=Em/3(1-2νm)，裂隙体积模量Kf=Ef/3(1-2νf)；σkk为应力张量；δij为克罗内可函数；基质比奥系数αm=1-K/Ks，Ks为煤粒的刚度。裂隙比奥系数αf=1-K/dKn，d为裂隙间的距离，Kn为裂隙的刚度；(εms、εfs)分别为基质中气体吸附引起的体积应变与裂隙中气体吸附引起的体积应变；αT为煤体热膨胀系数；ΔT表示温度变化量，T表示温度；pm、pf分别为基质气体压力和裂隙气体压力。根据朗格缪尔吸附理论[29]

(5)

(6)

(7)

(8)

其中：εms、εfs分别为基质的吸附应变与裂隙的吸附应变；εL为朗格缪尔应变常数；Vms、Vfs分别为基质中吸附气体在标准状况下所占的体积与裂隙中吸附气体在标准状况下所占的体积；VL为朗格缪尔体积常数；PL(T)为朗格缪尔压力。曲鸿雁等[16]定义其与温度T的关系为升温时

(9)

温度下降时

(10)

其中：PL0为初始温度时的朗格缪尔压力；Cc(T)为煤的热容；T为温度；T0为初始温度；R为理想气体常数。联立式(1)—式(4)得到煤体Navier形式解为

(11)

(12)

其中：umi，kk、ufi，kk分别为基质位移在主位移方向上导数的和与裂隙位移在主位移方向上导数的和；umk，ki、ufm，ki分别表示基质位移在切应力方向上导数的和与裂隙位移在切应力方向上导数的和；pm，i为基质气体压力在i方向上的导数；pf，i为裂隙气体压力在i方向上的导数。

1.2 气体流动方程

裂隙系统与基质系统内气体质量交换通过源汇项实现，包括流动项与吸附项。裂隙气体与基质气体的质量守恒[26]分别表示为

(13)

(14)

其中：φm、φf分别为基质孔隙度与裂隙孔隙度；ρ表示密度，ρm、ρf分别为基质气体密度与裂隙气体密度，t为时间；qm为基质气体流速；qf为裂隙气体流速；Qm、Qf分别为裂隙与基质间的气体质量交换；Qms、Qfs分别为裂隙与基质的气体吸附量。据理想气体状态方程

(15)

其中，Mg为气体相对分子质量。根据达西定律定义，基质气体流速qm，裂隙气体流速qf[2]分别为

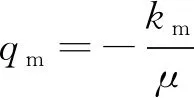
(16)

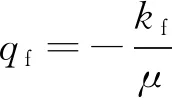
(17)

其中：km、kf分别为基质渗透率与裂隙渗透率；μ为气体的黏度。

裂隙与基质间的气体质量交换Qm、Qf[30]可以分别表示为

(18)

(19)

其中，τ为气体扩散时间。

裂隙与基质的气体吸附量Qms、Qfs可以分别表示为

(20)

(21)

其中：ps、TS分别为标准状况下的压力与温度；ρcm、ρcf分别为基质的密度与裂隙的密度。将式(15)—式(21)代入式(13)—式(14)得到流动方程

(22)

(23)

1.3 孔隙度与渗透率方程

煤的裂隙孔隙度与基质孔隙度分别定义为煤应变的函数[31]

φf=φf0+αfΔεfe

(24)

φm=φm0+αmΔεme

(25)

其中：Δεfe、Δεme分别为裂隙有效应变变化量与基质有效应变变化量[28]；φf0、φm0分别为裂隙初始孔隙度与基质初始孔隙度。

(26)

(27)

其中：Δεfv、Δεmv分别为裂隙体积应变变化量与基质体积应变变化量；Δεfs、Δεms分别为裂隙吸附应变变化量与基质吸附应变变化量；αTΔT为热应变；clf、clm分别为吸附应变对裂隙和基质的影响因子

(28)

(29)

其中，Δpmax表示压力的最大差值。

根据孔隙度与渗透率的关系

(30)

(31)

其中：kf0、km0分别为裂隙初始渗透率与基质初始渗透率。

1.4 热量流动方程

煤-气系统的储热项包括煤裂隙、裂隙气体、煤基质体与基质气体。考虑到煤结构较为致密，假设4个储热项在无限小的局域内具有良好的相互导热性，即在任一时刻、同一计算单元中，煤裂隙、煤基质、裂隙气体和基质气体彼此温度相同，气体的热对流也以裂隙气体为主。考虑热量的产生与流动的方程定义为

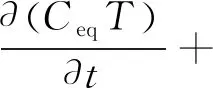
(32)

其中，Ceq为等效热容；Keq为等效导热系数；CL为体积热容；QH为吸附解吸产生的热源汇；QG为煤层与恒温地层热交换时所产生的热源汇。等效热容Ceq定义为

Ceq=(1-φf-φm)ρcCc+(φfρgf+φmρgm)Cg

(33)

其中，ρc为煤的密度；Cc、Cg分别为煤的热容与气体的热容。

等效导热系数Keq可以定义为

Keq=(1-φf-φm)Kc+(φf+φm)Kg

(34)

其中，Kg、Kc分别为气体的导热系数与煤的导热系数。

吸附热QH可以定义为

(35)

图2为各物理场之间的耦合关系，研究吸附热引起的温度变化如何在该物理关系中产生影响，量化该影响并探究其对煤吸附解吸气体相关研究的意义。

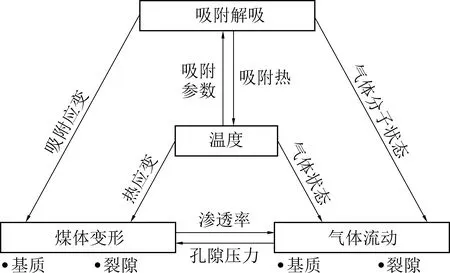
图2 多物理场耦合关系图

2 模型验证

2.1 数值模拟

煤体吸附气体产热过程可以通过室内试验直接观测[32]。已提出的耦合模型的可靠性可对比已有的试验数据进行验证。依据文献[32]中测试条件，将圆柱煤样简化为二维旋转对称模型，模型一端注气，其他边界无位移且无气体质量交换。注气端自由，其他边界受夹持器影响无切向位移。煤柱侧面在保温棉的包围下与环境无热量交换，注气端保持室温，底端盖玻璃片与外部保持热量流动，见表1。

表1 模拟边界条件

模型示意如图3所示。

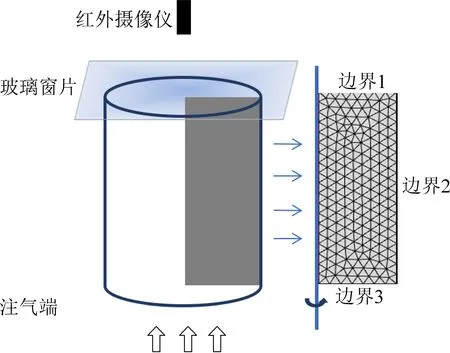
图3 热传递室内试验模型

相关系数如下：

甲烷比热容Cgch4(J·kg-1·K-1)2 160[33]煤导热系数Kc(W·K-1·m-1)0.191 3[34]甲烷导热系数Kg/(W·K-1·m-1)0.037 1[34]基质初始孔隙度øm00.01裂隙初始孔隙度øf00.02基质初始渗透率km0/m21.5×10-16[35]裂隙初始渗透率kf0/m21.4×10-15[34]煤泊松比νm0.339 4[34]煤体热膨胀系数αT/(1·K-1) 9×10-5[34]初始朗格缪尔压力PL0/MPa2.1[34]朗格缪尔应变常数εL/(m3·kg-1)0.023 7[34]二氧化碳比热容Cgco2/(J·kg-1·K-1)844[33]二氧化碳相对分子质量Mg44二氧化碳导热系数Kg/(W·K-1·m-1)0.016 8[33]初始温度T0/K293.15甲烷黏度μ/(Pa·s)1.2×10-5[33]甲烷吸附热值q/(kJ·mol-1)8.1[33]基质比奥系数αm0.667裂隙比奥系数αf0.3基质弹性模量Em/MPa2 713[33]裂隙弹性模量Ef/GPa1.416[33]煤粒弹性模量Es/GPa8.139[33]甲烷相对分子质量Mg16[33]理想气体常数R/(J·m-1·K-1)8.314 41[33]煤比热容Cc/(J·kg-1·K-1)1 000二氧化碳吸附热值q/(kJ·mol-1)19.2[33]二氧化碳黏度μ/(Pa·s)1.37×10-5[33]

2.2 模拟结果

数值模拟的煤体温度变化如图4所示，可以看出模拟结果与实测数据具有较高度的拟合度，模拟需要的相关系数见表2。甲烷注入煤体后将导致复杂的热量流动、固体变形吸附甲烷过程将导致煤体积变化、吸附热变形、吸附产热功率与热损失根据温度随时间变化特征，可分为4个阶段：

第1阶段：在甲烷注入煤体的前40～60 s，甲烷分子迅速吸附于煤表面，导致煤体温度随即升高。注气压力越高，煤体温度升幅越大(图4)。在气体吸附与吸附放热共同影响下，煤体积迅速膨胀，之后趋于平稳(图5)。其中，吸附热引起煤体积变形随温度变化正相关(图6)。吸附放热功率在注气初始阶段先迅速增加，随后回至0。在此过程中，吸附热开始经过吸附罐外壳向外界传导，热损失通量表现为先增大，后降低过程。

图4 煤表面温度随时间变化曲线

图5 体积应变随时间变化曲线

图6 热应变随时间变化曲线

第2阶段：煤体温度从峰值开始下降，吸附放热功率接近0，这说明注入甲烷在煤体内部吸附趋于平衡状态(图7)。热通量逐渐增加至0(图8)，这说明，吸附罐内聚集热量向环境传导速率放缓。导致温度下降，煤的热膨胀应变变小。

图8 边界热通量随时间变化曲线

第3阶段：在降压持续时间约60 s过程中，吸附态甲烷从煤表面解吸。与吸附放热过程相反，吸附态气体分子需要吸收热量才能转换为游离态。由图7可知，在降压初始阶段，煤的吸附热功率负向增大。气体压力越高，吸附热功率增幅越大。与此同时，热通量正向增大，表明煤从环境吸收热量(图7)。受吸附气体解吸与温度降低共同影响，煤样体积在此阶段持续收缩。

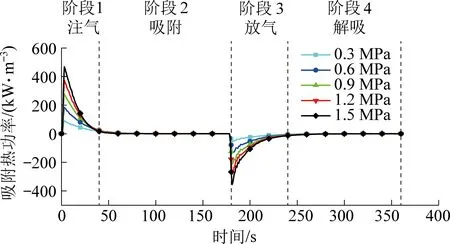
图7 吸附热功率随时间变化曲线

第4阶段，吸附罐内压力恢复至常压后，煤体内吸附气体解吸过程趋于停滞，煤体温度也随之平衡。在较高注气压力条件下，最终的平衡温度会低于初始温度。这可能是由于较大压降排出气体较多，损失较多热量。

由上述过程可知，吸附热引起煤体温度变化主要来自2个因素：一方面是气体压力梯度因素，由图7知较高的注气压力可以提供更快的吸附速率，发热功率随之增大，升温速率加快。同样，在解吸阶段较高的压降也可以增大吸热功率，降温幅度更为明显。另一方面是与环境热交换因素，由图8知注气压力越高，吸附热量流动越快。对第1与第3阶段，甲烷吸附/解吸诱发的放/吸热是导致温度变化的主要原因。对第2与第4阶段，由于吸附/解吸过程趋于平衡，温差逐渐减小，热量损耗变慢。热量传递成为导致温度变化的主要原因。

此外，气体吸附-解吸过程也影响煤体积变化。煤体骨架受力学压缩、吸附膨胀与热膨胀3者控制。对于吸附阶段，注气压力升高会压缩煤体积，但同时也会增加吸附热膨胀与吸附膨胀；对于解吸阶段，气压降低会减弱煤的力学压缩变形，同时伴随解吸收缩变形与吸热收缩变形。

3 分析算例

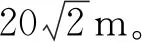
图9 模拟模型示意

3.1 恒定注气压力条件

煤储层压力的初始值设定为0.1 MPa，初始温度293.15 K，将8 MPa压力的二氧化碳持续注入2 000 d。图10a所展示的测量点温度变化情况显示，二氧化碳吸附产热过程导致该点温度明显上升，最大温升约为14 K。图10b为吸附热对吸附量的影响，反映了二氧化碳地质封存效果。经过对比未考虑吸附热时煤层吸附气体量，可以看出单位体积煤体对二氧化碳的吸附性能被升高的温度削弱了约14.05%。图10c为吸附热对裂隙渗透率的影响。虽然吸附热量聚集会降低煤的吸附气体能力，进而减弱煤的吸附膨胀应变，但吸附热会导致煤体热膨胀加剧，热膨胀在该竞争控制中占据优势。在该种情况下，被气体压力撑开的裂隙通道由于煤粒的热膨胀反而呈现出渗透率先下降的趋势。这说明未考虑吸附热的数值模型将高估煤储层渗透率。在吸附热的影响下导致二氧化碳注入效率降低。由图10d可知，吸附热效应导致注入量只有恒温条件下的83.2%。

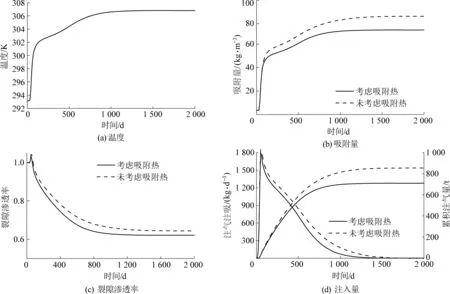
图10 恒定注气压力条件

3.2 恒定注气速率条件

图11为以速率30 kt/a(即1.285 kg/s)持续注气800 d过程中煤储层温度、吸附气体量与渗透率变化情况。由于该注入条件要求不断调整注气压力，以保证注气速率不变，导致煤储层物理性质持续动态变化。由图11a可知，煤层温度快速上升，在800 d时，温度上升10.8 K。持续升温会减弱煤层吸附性能，同时增加煤骨架的热膨胀(图11b)。在此过程中，裂隙渗透率表现为初期短时减小后快速增加，接着持续降低过程(图11c)。由于煤储层渗透率的持续降低，导致注气压力持续升高至7.2 MPa(图11d)。经过对比可以发现，忽略吸附热时注气压力可达6.2 MPa。

图11 恒定注气速率条件

4 结 论

1)气体在煤表面的吸附放热/解吸吸热过程会改变煤体温度，动态影响吸附/解吸进程。对于吸附过程，注气压力越大，升温越显著；对于解吸过程，降压越大，降温幅度越大。在整个吸附/解吸过程中，煤体积变化是吸附膨胀与热膨胀共同作用的结果。

2)吸附热引起的煤储层温度升高会产生连锁反应并会随着时间和尺度增大而放大。数值模拟结果表明，二氧化碳吸附放热会导致孔隙度因热膨胀而减小，使注入气体运移受阻。温度升高还减弱煤对二氧化碳的吸附能力。对比考虑吸附热模型与未考虑吸附热模型结果，恒压注气中累计注气量的差异随着时间推移逐渐增加。定速注气中注气压力的差异也随时间逐渐增加。忽略吸附热将高估注气效率。

3)在二氧化碳地质封存时，降低储层温度可以提高封存效果。煤对气体的吸附量与温度和压力有关。在吸附放热不可避免地升高煤层温度的情况下，适当地对煤层进行降温将有利于吸附过程的进行，提高封存效率。