近水平煤层露天矿中间搭桥高度研究
李胤达 ,韩 流,尚 涛,陈树召
(中国矿业大学 矿业工程学院, 江苏 徐州 221116)
0 引 言
露天矿内排土场的搭桥运输系统形式多样,桥体形状数量各异[1],就搭单桥而言,根据搭桥目的可分为3类。第1类为露天矿端帮具备双环运输条件,但工作线较长(超大型露天煤矿[2])时,为了减小运输成本,通过在矿坑中部搭建运输桥体,将工作帮和排土场工作平盘进行分割,缩短内排时在其上部的运输距离[3-4],这种内排搭桥方式桥体高度设置灵活,承担工作帮部分剥离物料运输任务。第2类为端帮进行靠帮开采时,取消部分端帮运输道路,为了避免剥离物料折返运距(高程)急剧加大的问题,在取消端帮运输道路的水平建立搭桥运输系统[5-6]。这种内排搭桥方式桥体高度设置较为局限,主要承担增加折返运距(高程)的剥离物料运输任务,减少折返运输费用。当靠帮开采制约排土效率时,这种桥体还可以起到恢复产能的作用[7]。第3类为露天矿存在靠帮开采条件,但主采煤层层数较多,且层位较为分散时,采取多水平局部靠帮,即将部分端帮运输道路由双车道改为单车道,同时建立搭桥运输系统,这种搭桥方式兼顾了前两种的特点,但对煤层赋存条件要求严格。内排土场的搭桥运输系统还具有一定的压制内排土场的作用,从而能够提高内排土场的稳定性[8-10]。
学者们对露天矿搭桥运输系统进行了大量研究,基于剥离物料重心运移假设,张宝卫[11]针对哈尔乌素露天煤矿建立了搭单桥和双桥运距和费用模型,对比得出中间搭单桥方案更适合该露天矿;刘福明等[12]按照剥离物料4等分原则建立近水平露天矿中间搭桥模型,提出适合中间搭桥的露天矿在工作线长度、煤层赋存条件以及工艺系统方面须具备的基本条件;钮景付等[13]基于哈尔乌素露天矿生产实际建立了梯形剥离物料搭桥运输功模型,丰富了搭桥运输系统的应用范围;周伟等[14]指出了搭桥运输系统的部分参数设置原则,完善了该系统的设计思路;赵彦合等[15]根据迈步搭桥式内排的两种基本形式,得出了迈步搭桥式内排运距的计算公式;傅新华等[16]研究了中间搭桥条件下露天矿基建前期松散层剥离延深方式,有效缩短了运输距离;常治国等[17-18]提出了搭桥方式连通端帮与内排土场开拓运输通道,有效降低了部分剥离物内排运距,提出桥移设步距准则,建立移设步距经济效益方程。露天矿二次剥离现象较为常见,李福平等[19]以留沟内排条件下的单环运输和内排搭桥2种方案为前提,构建了实现最小二次剥离量的内排留沟高度优化模型;顾正洪等[20]分析了压帮高度与工作线长度、重复剥离端帮角和重复剥离时间的相互关系,对端帮内排二次剥离进行了研究,得出了不同条件下最佳压帮高度的取值范围。
上述研究较为精准地建立了内排搭桥运距、运输功模型,根据桥体个数、形状、适用性进行分类探讨,分析了桥体适用条件及优化参数,并且对搭桥运输系统运行方式进行了较为深入的研究,成果显著。但上述所有的运距计算模型都假设桥体服务台阶上的剥离物料分界点固定,从而减少了桥体的服务范围,且对桥体的拆除方案不够优化。因此,笔者基于近水平露天矿双环运输条件下的搭桥问题进行深入系统研究,通过运输功最小原则建立动态剥离物料分界点计算方法,利用该方法建立运输功模型,得出桥体最大服务范围;优化拆桥方案并建立拆桥费用模型;综合考虑运输费用和搭桥费用,得出最佳搭桥高度,使近水平露天矿搭桥运输系统发挥最大的价值,为内排搭桥运输系统的实施和推广提供理论和技术支撑。
1 搭桥运输系统模型建立
1.1 运输功模型
1.1.1 搭桥运输功模型
搭桥运输系统各参数空间几何关系如图1所示。以坑底标高为零基准、一次搭桥循环时间建立运输功模型,设桥体高度为H、沿工作面走向单位长度上的剥离物料质量为G(一次搭桥循环时间内),建立桥体服务范围内h水平运输参数模型。工作面平盘长度为Dw

图1 中间搭桥运输系统
Dw=L0+h(cotα1+cotα2)
(1)
式中:L0为坑底长度,m;α1、α2分别为工作面两侧端帮稳定帮坡角,(°)。
端帮运输道路长度为De,即
(2)
式中:c为坑底宽度,m;β1为工作帮台阶角,(°);β2为排土场台阶角,(°);hw、hd分别为工作帮台阶高度和排土场台阶高度,m;a、b分别为工作帮平盘宽度和排土场平台宽度,m。
桥面运输通道长度为Dm,即
(3)
排土场平台长度为Dd,即
Dd=Dw
(4)
1)当h≥H,即工作面水平高于桥面水平时,该水平的剥离物料先由工作帮折返运输至桥面水平,后在排土场折返运输到达排弃水平,折返运距包括平行和垂直于工作面的折返运距。随着高差(工作面与桥面)的增大,折返运距的增大过程分为2个阶段:初期高差较小时,折返运距小于等于剥离物料重心到桥面中心线的水平距离,此时剥离物料的折返运距,按物料重心到桥面中心线的水平距离计算;随着高差增加,折返运距也增大,当折返运距大于剥离物料重心到桥面中心线的水平距离时,物料在工作帮的运输距离按折返运距计算。同理,排土场运距计算方法。
中间搭桥运输系统桥体两侧对称,分析时只需考虑其中一侧即可。根据上述运距计算原理,设x为剥离物料分界点距桥体中心线的距离与同水平总物料长度之比,则桥面以上高程为h水平物料,当折返运距小于等于剥离重心到桥体中心线距离时的运距模型为
(5)
且有A=(h-H)(a+hwcosβ1)/hw,B=(h-H)×(b+hdcosβ2)/hd
折返运距大于剥离重心到桥体距离时的运距模型为
(6)
式中:Lw为工作帮运距,m;Lm为中间桥运距,m;Ld为排土场运距,m;i为折返运输斜坡道坡度,取8%。
h水平物料通过端帮道路运输时的运距模型为
(7)
式中:lw为工作帮运距,m;le为端帮路运距,m;ld为排土场运距,m。
h水平的剥离物料总运输功为Wh,即
Wh(x)=DwxGLA+Dw(1-x)GLB
(8)
且有LA=Ld+Lm+Lw;LB=ld+le+lw
将式(5)代入式(8),化简解得Wh取最小值时,得
x=0.5
(9)
即折返运距小于等于剥离重心到桥体中心线距离时,h水平剥离物料运输分界点为工作面台阶走向的中点。将式(6)代入式(8),同理化简解得Wh取最小值时,有
(10)
即折返运距大于剥离重心到桥体中心线距离时,此位置为剥离物料运输分界点。
2)当h 利用对称性只需对桥体一侧进行建模,桥体的一部分为桥面以下水平的剥离物料,不参与内排运输,因此桥面以下水平的剥离运输量与不搭桥相比有所减少。又因桥体横截面为等腰梯形,所以桥体以下剥离水平与桥面水平高差越大,剥离量减少越多。桥面以下高程为h水平物料通过中间桥运输,且折返运距小于等于剥离重心到桥体中心线距离时的运距模型为 (11) 折返运距大于剥离重心到桥体距离时的运距模型为 (12) h水平物料通过端帮运输时的运距模型为 (13) 式中:f为桥面宽度,m;β3为桥体坡面角,(°)。 设h水平剥离物料总运输功为Wh,即 Wh(x)=G[Dw-2(H-h)cotβ3-f][xLA+(1-x)LB] (14) 将式(11)代入式(14),化简解得Wh取最小值时,即 (15) 即h水平的物料通过中间桥运输,且折返运距小于等于剥离重心到桥体距离时,该位置为剥离分界点;将式(12)代入式(14),同理化简解得Wh取最小值时,有 (16) 故折返运距大于剥离重心到桥体中心线距离时,此位置为剥离分界点。 1.1.2 双环运输功模型 在双环运输系统中,工作帮剥离物料分界点位于工作帮的中间位置,两侧的剥离物料重心位于其中心,利用等标高排弃原则,得出双环运输条件下,h水平剥离物料总运输功wh的计算公式为 (17) 1.1.3 节省运输费用模型 运输费用只考虑参与运输的剥离物料,所以计算时不考虑位于桥体服务范围内的煤层赋存台阶,在搭桥运输系统服务的最高与最低水平处节省运输费用计算为 Q1=(wh-Wh)q1 (18) 式中:Q1为节省运输费用,元;q1为单位运输功的运输费用,元。 以单层煤结构建立模型,计算合理的二次剥离深度hT,桥体交界面参数及资源回收方式如图2所示,β4为混合桥体侧的剥离物料部分,在桥体走向方向坡面的稳定坡面角,β5、β6分别为混合桥体侧的压煤部分和压煤桥体,在桥体走向方向坡面的稳定坡面角。根据拆桥费用最小原则,引入经济合理二次剥采比概念,其意义是表示经济上允许的最大二次剥离量与采矿量之比,其按煤炭利润计算公式为 nT=QMρ/QB (19) 式中:nT为经济合理二次剥采比;ρ为煤的容重,t/m3;QM为吨煤利润,元/t;QB为单位体积的剥离费用,元/m3。 经济合理二次剥采比也是一个微观概念,即保证收益条件下增加二次剥离深度Δh,引起的二次剥离物料体积与资源回收量的最大比值,从而求出拆桥二次剥离边界。微观概念下的经济合理二次剥采比公式为 (20) 且有 式中:hR为煤层顶板高程,m;hB为煤层底板高程,m。 二次剥离边界由2个等腰梯形平面组成,如图2所示,最上部梯形为剥离物料桥体部分,中间部分为压煤部分的煤层上覆岩层(当拆桥二次剥离深度到达最下煤层时这部分岩石层不存在),最下部分为煤层。由经济合理二次剥采比的利润求法和剥离边界值求法建立等式,求出合理的二次剥离深度hT过程如下: 图2 交界面资源回收示意 将式(19)代入式(20)化简,得 (21) 且有E=cotβ4-cotβ5 式(20)表示的二次函数曲线对称轴为正值,由于hR和hB取值不同,所以该二次函数的根,即式(21)有2种结果,当有2个正根时,hT的值取较小的正根,当2个根一正一负时,hT的值取正根。 与不采用搭桥运输系统的开采方式相比,桥体拆除引起的费用主要由三部分组成,其中二次剥离量和损失资源量会导致生产成本增加,减少岩石剥离量会导致生产成本降低。各部分体积计算可利用积分求得,计算公式如下: (22) (23) (24) 式中:Vt、Ve、Vs分别为搭桥运输系统在桥体拆除时引起的二次剥离量、少采资源量和少剥离量,m3。 式(23)中,当煤层顶板高度hR大于二次剥离高度时,积分上限用hT代替。 根据体积量可以计算一次搭桥循环的拆桥费用为 Q2=Vtq2+Veρq3-Vtq4 (25) 式中:Q2为搭桥费用,元;q2、q4为表示单位体积二次剥离费用和单位体积的剥离费用,元/m3;q3为吨煤利润,元/t。 宝日希勒露天煤矿位于内蒙古自治区呼伦贝尔市北部,距市中心15 km,是我国重要的大型煤电基地之一。该露天煤矿煤层为近水平赋存状态,全矿地质条件简单,主采煤层有3层,从上至下分别为12煤,平均厚度23.29 m;21煤,平均厚度4 m;31煤,平均厚度8.05 m。其中12煤全区可采,工作线长度达2 700 m,21煤和31煤局部可采,其工作线布置于矿坑北部,长度分别为930 m和700 m,局部可采煤层年产量约占全矿年产量的11%。矿坑北部由于局部可采煤层的存在,坑底较深,31煤底板平均高程为+461 m,矿坑南部只开采12煤,坑底为12煤底板,平均高程+538 m。宝日希勒露天煤矿开采参数如下。 工作线长度L/m2 700端帮边坡角α/(°)24工作平盘宽度a/m70工作帮台阶坡面角β1/(°)70工作帮台阶高度hw/m15排土平台宽度b/m50排土台阶坡面角β2/(°)33排土台阶高度hd/m15坑底距c/m80桥面宽度f/m45运输费用q1/(元·t-1·km-1)1.2二次剥离费用q2/(元·m-3)6剥离费用q4/(元·m-3)22吨煤利润q3/(元·t-1)50 宝日希勒露天煤矿2019年12煤层上覆剥离物料为2 100万m3,21煤和31煤层上覆剥离物料共200万m3,为了降低剥离物料的运输成本,该露天煤矿在南、北采坑深度过渡位置处,设置搭桥运输系统,从而减少主要剥离物料的运距,即12煤层上覆剥离物料的工作面运输距离,桥体基底为南部采坑的坑底。据理论模型可知,桥体越高服务范围越大,节省运输费用越多,但搭桥费用也会增大,因此该露天煤矿搭桥运输系统的搭桥高度存在最优值。 宝日希勒露天煤矿存在全区可采和局部可采煤层,导致排土场工作线不平行于工作帮发展,北部排土场较为滞后。因此利用叠加原理,将该露天煤矿简化为两个不同开采规模的露天矿的一部分,即桥体北侧是工作线为2 400 m露天矿的1/2(以中间桥为界划分),1/2工作线长度为1 200 m;桥体南侧是工作线为3 000 m的露天矿1/2(以中间桥为界划分),二分之一工作线长度为1 500 m,两个二分之一工作线之和即为12煤工作线长度2 700 m。简化之后的两部分,利用节省费用模型和搭桥费用模型,根据收益最大化原则得出宝日希勒露天煤矿搭桥运输系统最佳搭桥高度。 宝日希勒露天煤矿12煤层划分为10、15 m两个台阶,该煤层上部剥离台阶为15 m,所以桥体最低高度为25 m,桥面搭接于煤层顶板,其余可用于搭桥运输系统的桥体高度依次以15 m高差递增,直至地表,因此,搭桥方案中桥体高度为25、40、55、70、85、100 m。首先,计算桥体南侧、北侧采坑不同桥体高度所对应的服务范围,利用式(9)、式(10)、式(15)、式(16)分别计算各桥体服务范围的剥离物料分界点至桥体中心线的距离与同水平物料点度之比x时的位置,此分界点位置的极限已不能布置斜坡道为判断标准,极限分界点位置所在的台阶,即为桥体所服务台阶范围的边界。通过计算得出桥体南侧、北侧各台阶剥离分界点位置如图3所示。 图3a中桥体南侧+563 m以下台阶全部为12煤层,所以不需要计算煤层的剥离物料分界点,而图3b中桥体北侧+563 m台阶以下存在12煤层、21煤层、31煤层以及各煤层之间的岩层,当桥体高度较低时,如桥体高度为25 m时,其服务范围可以包含12煤层下部的+528 m剥离台阶。桥体南侧、北侧+653 m水平以上台阶已经到达地表,且由于第四系覆盖层薄厚不均匀,其上部台阶不存在或不完整,所以计算服务范围时不考虑+653 m水平以上台阶。由图3可以看出,随着桥体高度的增加,桥体服务范围整体提高,且由于存在12煤层下限和地表上限,随着桥体高度的增加,桥体服务范围内的台阶数呈现由少变多再变少的规律。 图3 台阶剥离分界点位置 结合已求出的剥离分界点位置,利用节省运输费用模型,计算出一次搭桥循环时间内,不同桥体高度时,桥体南侧和北侧节省的运输费用(由于桥体南侧、北侧为两个不同开采规模的露天矿的一部分,所以采用模型计算结果值的二分之一)。计算结果如图4所示。台阶高度与桥体高差越大,折返距离越大,抵消掉工作面节省的运距就越多,所以图中桥体服务范围内,某一台阶所节省的运输费用,随着该台阶高度与桥体高差的增大而减小;桥体越高,桥面与工作帮搭接位置处的工作线越长,工作面节省运距就越大,在图中表现为不同桥体节省费用的最大值随桥体高度的增加而增大。 图4 不同桥体高度节省运输费用 利用搭桥费用模型,计算出二次经济合理剥采比为12.5,代入式(25),求出不同桥体高度时的二次剥离深度hT,通过式(22)—式(24)得出二次剥离量、少采出资源量和少剥离量,根据实际单价求出一次搭桥循环时间内各桥体高度所对应的搭桥费用。计算结果见表2 。 表2 不同桥体高度搭桥费用 通过节省运输费用与搭桥费用,计算宝日希勒露天煤矿搭桥运输系统不同搭桥高度下的收益,采用收益收益最大原则得出当桥体高度为70 m时为合理高度,又考虑桥体高度为55 m时,与70 m桥体高度相比收益仅减少1%,但二次剥离工程量较小,用时较短。最终推荐宝日希勒露天煤矿搭桥运输系统桥体高度的最佳值为55 m。 1)以坑底水平为基准,考虑不同水平到桥面折返距离的动态变化,依据运输功最小原则,得出不同工作面的剥离物料的动态分界位置,并在此基础上建立内排运输功计算模型,该模型扩大了搭桥运输系统的服务范围,突破了传统搭桥运输系统只服务其上部水平的局限性,节省了传统固定剥离物料分界点原则下的运输功。 2)考虑桥体搭接位置处的形状、组成桥体的成分及二次剥离过程3个方面的影响因素,根据吨煤利润和二次剥离成本,提出经济合理二次剥采比计算方法,该方法优化了拆桥方式,降低了搭桥费用。以经济合理二次剥采比为边界值,计算出桥体搭接处合理的二次剥离深度,从而优化了搭桥费用模型。 3)针对宝日希勒露天煤矿的实际开采现状,采用叠加原理,通过运输功模型和搭桥费用模型计算得出该露天矿采用搭桥运输系统时,随着桥体高度的增加,桥体服务范围整体提高,且服务范围内的台阶数呈现由少变多再变少的规律;针对某一台阶所节省的运输费用,随着该台阶高度与桥体高差的增大而减小;不同桥体节省费用的最大值随桥体高度的增加而增大。最终确定桥体高度为55 m,一次搭桥循环时间内增加收益最大,约2 901.5万元。1.2 搭桥费用模型
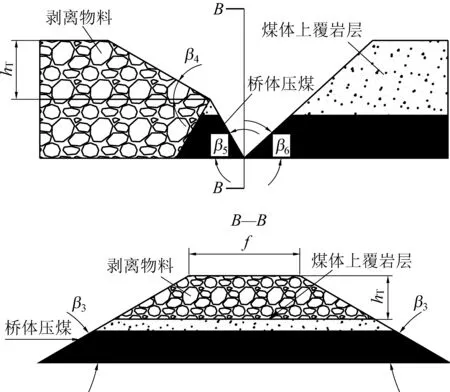
2 实例分析
2.1 宝日希勒露天煤矿生产条件

2.2 宝日希勒露天煤矿搭桥高度优化
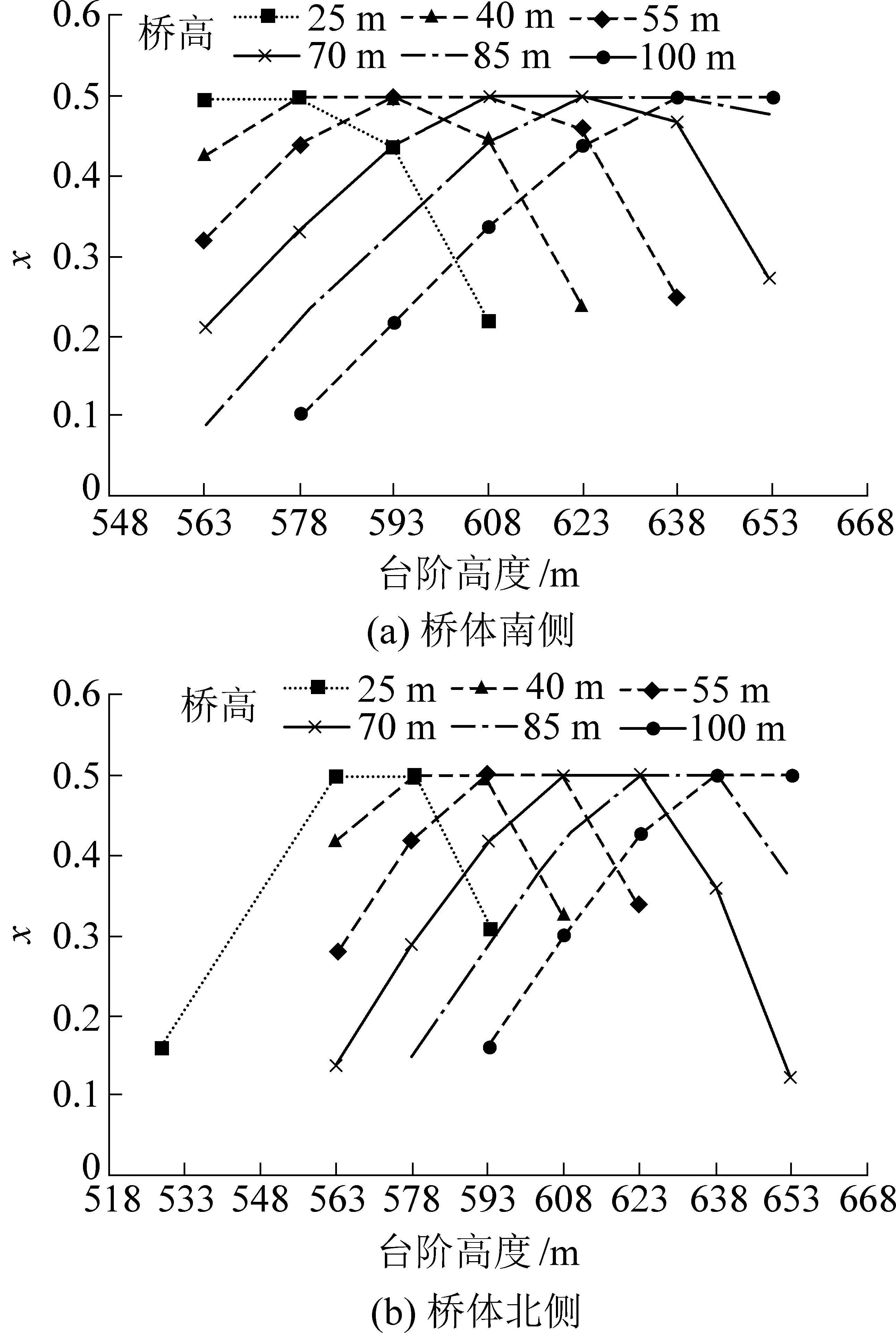
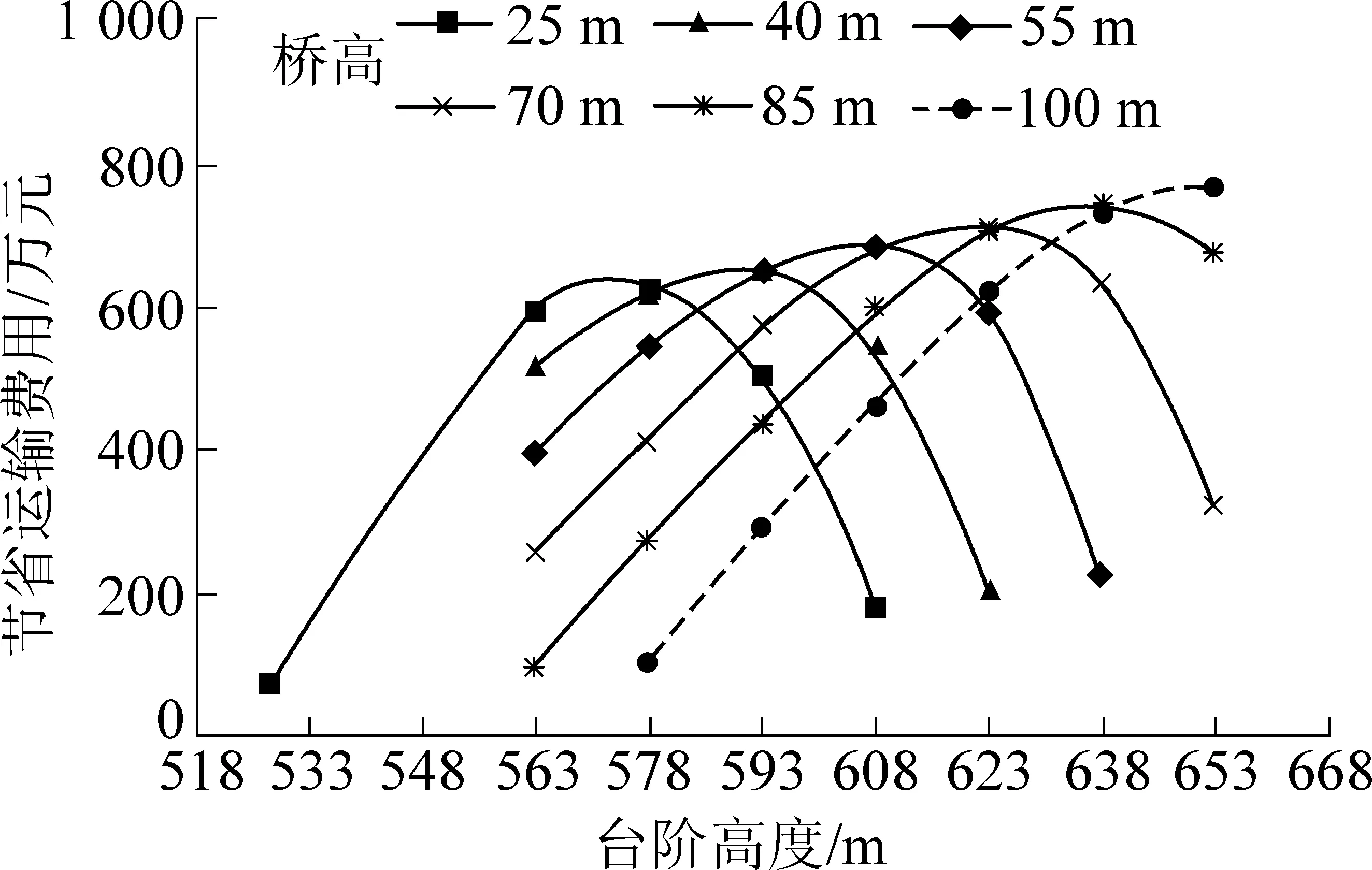

3 结 论

