基于虚拟样机技术的叉车转向桥动静态特性分析*

张增密，叶 俊，左改兵，吴 波，郭琰平

(安徽合力股份有限公司安庆车桥厂，安徽 安庆 246001)

0 引 言

叉车转向桥主要由转向桥体、连杆、转向油缸、转向节和转向轮毂组成，如图1所示为某公司设计研发的某型号叉车转向桥结构示意图。叉车转向桥在叉车转向过程中承受着复杂的交变载荷，设计过程中既要保证桥体具有足够的强度、刚度和疲劳强度以及良好的结构性能，同时还要保证转向桥体不会与外界环境产生共振现象[1]。因此，对转向桥体进行基于虚拟样机技术的动静态特性分析对提高叉车运行的安全性、平稳性具有十分重要的意义。

通常，国内外对于叉车转向桥体的分析大部分还是采用传统的理论计算分析和经验分析，根据理论计算分析桥体的静强度，对于动载荷一般采用理论计算乘以动载荷系数转化为静载荷计算分析，很难得到正确的分析结果[2]。本文创新之处采用虚拟样机分析技术，基于ADAMS技术对叉车转向桥进行多体动力学仿真分析，基于ANSYS Workbench技术对转向桥体进行动静态特性分析和研究。

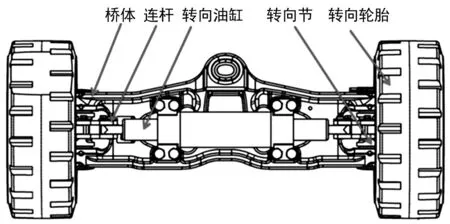
图1 转向桥结构示意图

1 转向桥体力学模型

转向桥在叉车行驶过程中，主要作用力有轮胎作用垂直向上的力F1、F2，转向过程中作用在左右轮胎上侧滑力T1、T2。对转向桥进行强度分析时，基于ANSYS Workbench分两种工况进行动静态特性分析，叉车空载时转向桥所受重力最大。

1.1 转向桥力学计算分析

(1) 工况一：最大垂向力

叉车空载时，此时作用在转向桥上的垂直力最大，由于在实际运行过程中，路面不平、轮胎弹性以及行驶速度等因素，应考虑载荷系数，本文载荷系数取3倍的最大载荷。

① 轮胎、主销处受力分析计算

F=2F0；F0L=F1L1+F2L2；F1=F2

(1)

② 转向桥体支撑轴处受力分析计算

F=F3+F4；F3L3=F4L4

(2)

1.2 基于虚拟样机技术的多体动力学仿真

(2) 工况二：最大侧滑力

叉车转向过程中，在离心力的作用下，转向桥的左右轮胎处于临界侧滑状态，此时轮胎上的侧滑力最大。由于该过程是一个复杂的受力过程，传统的理论计算很难找到最大时刻的力和状态。本文基于虚拟样机ADAMS多体动力学仿真分析技术，可以得到叉车转向桥在转向过程中的位移、速度、加速度以及各构件之间的受力随时间变化曲线关系[3]。如图2(a)所示为左右侧轮胎对转向桥体的垂直作用力随时间变化曲线；图2(b)为左侧轮胎所受侧滑力随时间变化曲线；图2(c)为右侧轮胎所受侧滑力随时间变化曲线。

图2 多体动力学仿真分析

1.3 分析结果

(1) 工况一：最大垂向力

本文以某公司某型号叉车转向桥为受力分析模型，根据该型号叉车参数，经过受力分析，得到地面对轮胎的作用力大小F0=28 665 N；主销对转向桥体主销座的作用力F1=F2=44 779.05 N。桥体支撑轴处作用力大小F3=26 140.18 N，F4=31 189.82 N。

(2) 工况二：最大侧滑力

如图2(a)所示为转向过程中，左侧轮胎对桥体的垂直向上的力最大为28 601.96 N，右侧轮胎对桥体的垂直向上的力最大为28 628.53 N。如图2(b)所示为转向过程中左轮胎侧滑力，左侧轮胎对桥体的X向侧滑力最大为11 017.66 N，Y向侧滑力最大为3 687.96 N。如图2(c)所示为转向桥过程中右轮胎侧滑力，右侧轮胎对桥体的X向最大侧滑力为7 723.21 N；右侧轮胎对桥体的Y向侧滑力最大值为5 785.01 N。表1所列为两种工况力参数。

表1 各工况受力参数

2 基于ANSYS Workbench静力学分析

将转向桥桥体模型导入ANSYS Workbench中。对其定义分析类型、网格划分、施加约束和载荷、求解、分析结果[4]。如图3所示为转向桥体网格划分图。如图4所示为转向桥体约束和加载位置示意图。

图3 网格划分 图4 约束加载

根据ANSYS Workbench对叉车转向桥体有限元分析，如图5所示为工况一桥体变形云图和应力云图，得出桥体的最大变形0～0.921 mm之间，最大变形主要出现在上主销座位置，桥体的最大应力值为263.07 MPa。如图6所示为工况二转向桥体变形云图和应力云图，得出桥体的最大变形0～0.805 mm之间，最大变形主要出现在右侧上主销座位置，桥体的最大应力值为294.25 MPa。

图5 工况一有限元分析

图6 工况二有限元分析

已知该转向桥为铸件转向桥体，转向桥体的材料为QT450，如表2所列为该材料的机械特性[5]。

表2 材料的机械性能 /MPa

依据GB10827-1999《机动工业车辆安全规范》，在叉车转向桥体设计时，选取安全系数[n]=1.5[6]。根据设计要求，所设计转向桥体安全系数n应大于许用安全系数[n]。

(3)

根据式(3)计算结果，工况一安全系数为n=1.71；工况二安全系数为n=1.53。该叉车转向桥体的应力值在允许范围内，满足其强度设计要求。

3 基于ANSYS Workbench谐响应分析

谐响应分析的主要目的就是确定叉车转向桥体结构的持续动力性能，使桥体避免因路面的固有频率而强迫振动引起共振造成桥体破坏[7]。对转向桥体的谐响应分析方法采用FULL法来分析。这种分析方法的优点是可不考虑主自由度或振型的选取[8]。

结构在简谐载荷作用下受迫振动的运动微分方程为[9]：

(4)

节点的位移响应为：

{X}={A}sin(θt+φ)

(5)

式中：{A}为位移幅值向量；φ为位移响应滞后激励载荷的相位角。

将式(5)带入式(4)可得到：

{A}=[-Mθ2sin(θt+φ)+Ksin(θt+φ)+

Bθcos(θt+φ)]-1.{F}sin(θt)

(6)

由式(5)可知设定一个频率范围和频率步，得到相应的幅值与频率之间的关系曲线，从曲线图中找到峰值所对应频率，再通过峰值对应的频率求得该频率下的应力值。

对转向桥体求解在0～800 Hz频率范围内的谐响应分析，频率载荷步长设置为10。如图7所示为转向桥体谐响应分析结果。由图可知，在0～530 Hz频率范围内，转向桥体变形随着频率的增大而增大，当频率为530 Hz时，此时第一次引起转向桥体的共振，转向桥体变形频率响应出现最大值，随后在530～540 Hz这段范围内出现下降趋势，紧接着550～770 Hz范围内又呈上升趋势，达到770 Hz第二次达到频率响应最大值。

图7 桥体变形频率响应曲线

在ANSYS Workbench中计算出第一次引起位移响应最大的频率“峰值”530 Hz时对应的应力。求解应变和应力的大小变化。如图8(a)所示，此时转向桥体的最大应变为0.035～1.703 mm。如图8(b)所示，此时转向桥体的最大应力为711.37 MPa。

图8 530 Hz频率下桥体谐响应

通过以上分析，得出当频率达到530 Hz时，引起的共振幅值达到最大。转向桥体在叉车运行过程中，需要避免产生该频率，以免发生共振现象，使得振幅过大破坏叉车转向桥体破坏而导致叉车运行过程的平稳性和安全性。

4 结 论

基于虚拟样机技术，利用ADAMS对转向桥进行多体动力学仿真分析，在此基础上利用ANSYS Workbench对转向桥体进行动静态特性分析。

根据虚拟样机技术的仿真分析结果，得出叉车转向桥体实际情况下主要分为两种工况。工况一主要受轮胎对桥体的垂直向上的作用力，此时桥体所受的最大应力为263.07 MPa，其强度安全系数为1.71。工况二主要是转向桥转向过程中受到最大侧滑力作用，此时转向桥体所受的最大应力为294.25 MPa，其安全系数为1.53。满足GB10827-1999《机动工业车辆安全规范》设计标准，进而验证了该转向桥体的结构设计满足安全性评估标准。

对该转向桥体进行谐响应分析，得出该桥体在频率为530 Hz时，应力频率响应和变形频率响应出现最大值，此时引起桥体的共振。在530 Hz频率时，此时桥体的最大变形为0.035～1.703 mm，最大应力值为711.37 MPa。在此频率下运行将引起桥体的共振，导致桥体结构发生很大程度上的破坏。实际使用过程中，由于路面不平引起的频率为15～30 Hz，此桥体共振频率远远大于路面频率，不会与路面之间发生共振，故此桥体设计合理。

基于虚拟样机技术的叉车转向桥体有限元分析为叉车转向桥体设计结构安全性评估，以及提高叉车运行过程中的平稳性和安全性，提供了更可靠的理论依据和参照，对提高新产品设计水平和提升叉车可靠性都具有很好的借鉴意义。