基于工艺过程分布图分析法的零件批量加工误差统计分析*

李双成, 陈兴媚

(广东理工学院 工业自动化系,广东 肇庆 526100)

0 引 言

机械零件在批量生产中由于多方面因素的原因，会给零件的加工精度带来不利影响，即零件的加工误差是多方面综合因素影响的结果[1]。其中不少因素的作用往往带有随机性，概率统计法在解决影响工艺系统受多方面综合因素作用产生的误差时，可以很好地与实际误差相吻合。通过结果的计算分析，不仅可以客观地评定工艺过程的加工精度，评定工序能力系数，还可以用来预测和控制零件的加工精度[2]。笔者利用工艺过程分布图分析法，通过小样本零件工艺过程的分析、计算来判别该批零件加工误差的性质，确定工序能力及其等级，估算出合格与不合格品率，对于改善零件批量生产中的加工精度、提高合格品生产效率均有重要意义。

1 加工误差的统计性质

按一批零件加工误差出现的规律性质来看，加工误差可分为两大类：系统性误差和随机性误差[3]。

1.1 系统性误差

系统性误差指连续加工一批零件时，如果加工误差的大小和方向保持不变或是按一定规律变化的误差；该误差又可分为两类：即常值系统性误差和变值系统性误差[4]。

1.1.1 常值系统性误差

常值系统性误差是指加工误差的大小和方向保持不变的误差[5]；如：原理误差，机床、刀具、夹具的制造误差、调整误差等，它们和加工的顺序(或加工时间)没有关系，故均为常值系统性误差。

1.1.2 变值系统性误差

变值系统性误差是指加工误差的大小和方向按一定的规律变化的误差[6]。如：机床、刀具的热变形，刀具的磨损等，都是随着加工的顺序(或加工时间)而有规律的变化，因此属于变值系统性误差。

1.2 随机性误差

随机性误差是指连续加工一批零件时，加工误差的大小和方向都是无规律地变化的误差。如：毛坯误差(余量大小不一、硬度不匀等)的复映，定位误差(基准面尺寸不一、间隙等)，夹紧误差(夹紧力大小不一)，多次调整的误差，内应力引起的变形误差等都是随机性误差[6-7]。这类误差产生的原因是随机的，从表面上来看没有规律，无从分析，但是应用数理统计的方法可以找出一批工件加工误差的总体规律，然后在工艺上采取措施加以控制。

2 工艺过程分布图法应用

例：在自动机床上加工一批尺寸为Φ(10±0.09) mm的工件，机床调整完后试车50件，测得尺寸列于表1中，试绘制分布曲线图、直方图、计算工序能力系数和废品率，并分析误差产生的原因[7～8]。

表1 一批零件加工尺寸结果 /mm

解：(1)剔除异常数据

在测量数据时有时会出现个别异常数据，在做统计分析之前应将其剔除，否则会影响数据的统计性质，异常数据都具有偶然性，它们与测量数据均值之间的差值若出现式(1)的情况即为异常数据：

≈10.0053 mm

(1)

按式(1)逐一校核得x3=10.129 mm,x31=10.141 mm为异常数据，将其剔除。

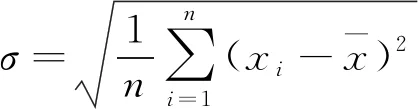
所以：σ=

≈0.031 7 mm

(2) 确定尺寸分组数及组距

把50个样本数据分成若干组，一般按照表2来选取。

由于n=48,查表2得k=7，则组距为：

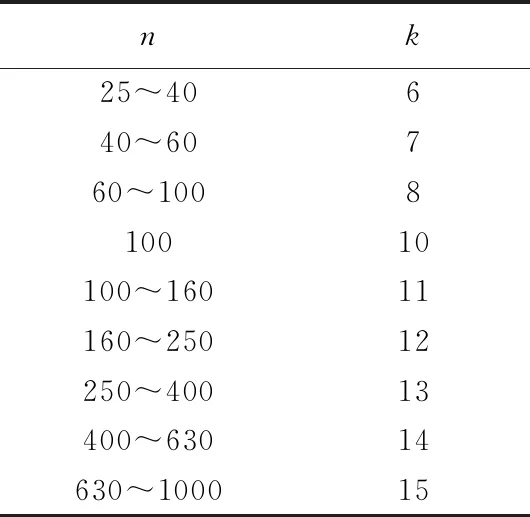
表2 样本容量n与分组数关系

(3) 绘制工件实际分布图

根据上述计算的分组数及组距，统计出各组尺寸的频数，列出频数分布见表3；并根据表3中的数据绘制出频数分布直方图如图1所示。

表3 频数分布表

(4) 工艺过程分析

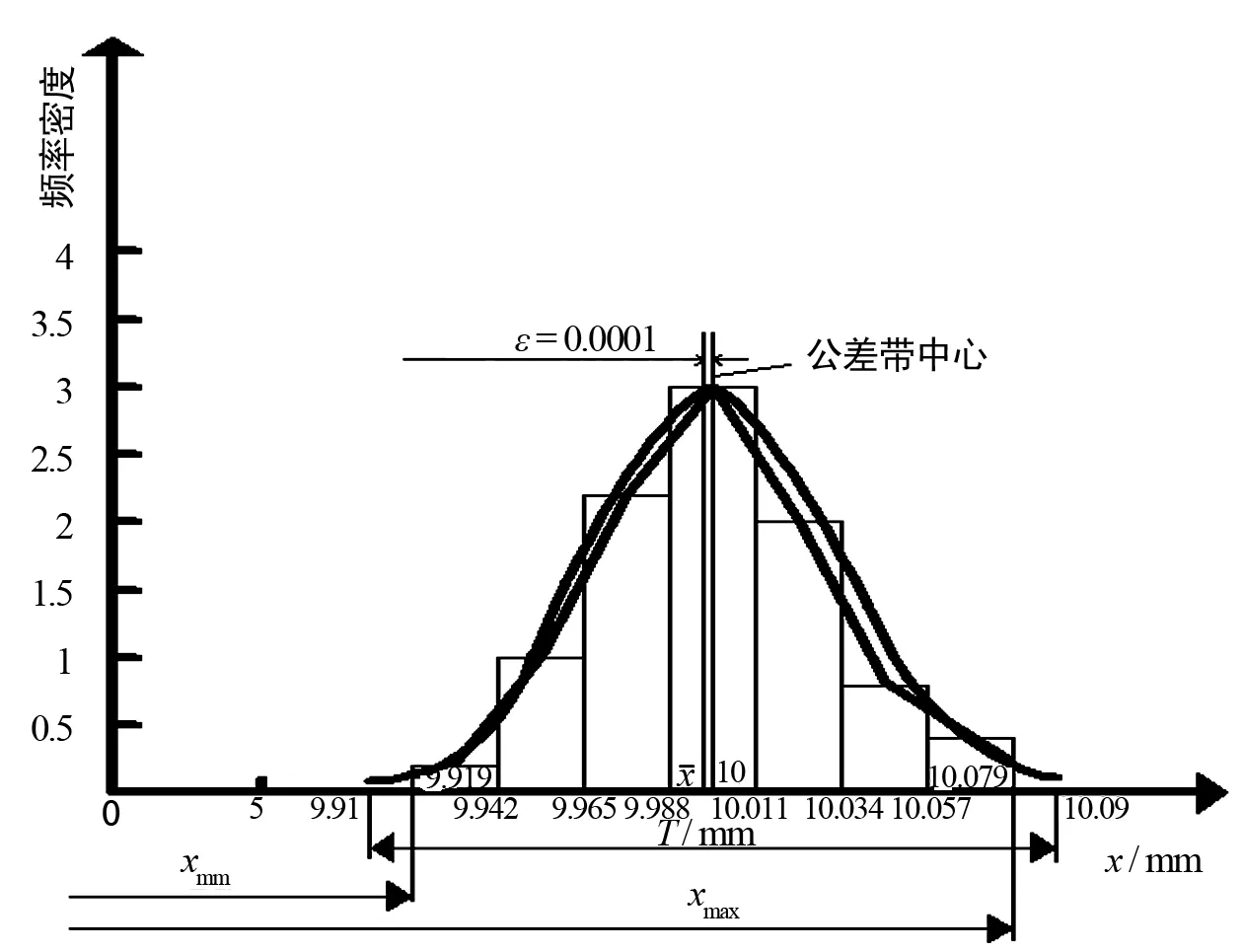
图1 频数分布直方图

② 确定工序能力及等级：工序能力是工序处于稳定状态时，加工误差正常波动值的幅度。可按式(2)来计算：

(2)

工序能力共分五级详见表4所列。

表4 工序能力等级

③ 调整机床精度系数E：机床调整精度系数可按式(3)计算：

(3)

ε许=0.5|T-6σ|

(4)

由式(4)可得：ε许=0.5|T-6σ|=0.5×|(0.18-6×0.031 7)|=0.005 1 mm。

而题目中尺寸分布中心相对于公差带中心的偏移量为：ε=0.000 1 mm。

所以：ε许>ε，故机床调整精度满足加工要求。

④ 估算合格与不合格品率：由图1频数分布图做变量变换得：

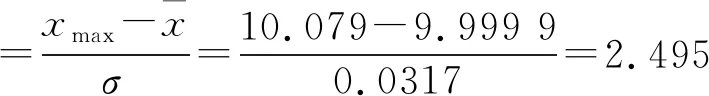
对于φ(2.552)根据表5经线性插值可得：

φ(Z)=φ(2.552)

=0.494 58

对于φ(2.495)根据表5经线性插值可得：

φ(Z)=φ(2.495)

=0.493 7

由此可得合格品率为：

H=0.494 58+0.493 7=98.828%

不合格品率为：B=1-98.828%=1.172%

(5) 减少不合品措施

① 提高工序能力 由前述可知工序能力为：

为三级工艺，属于工艺能力不足范畴，可能少量出现不合格品需要加以改进。改进方法可根据具体情况而定，如选择精度较高的机床，调整工艺装备、改变工艺参数或工序安排等，从根本上提高工艺能力[11]。

② 减少常值系统性误差 由图1可知尺寸分布中心与公差带中心存在偏差ε=0.000 1，尽管偏差数值不大于允许数值，但若能消除该偏差(如将车刀后退ε/2)，则可明显减少不合格频率。

③ 6σ原则 6σ的大小代表了某种加工方法在一定条件下(如毛坯余量、切削用量，正常的机床、夹具、刀具等)下所能达到的加工精度。所以在一般情况下，应使所选择的加工方法的标准差σ与公差带宽度T之间满足关系6σ≤T[12-13]。

表数值

3 结 语

用工艺过程分布图法分析零件加工质量有很多优势:它能很好地判断零件加工误差的性质，并能够用来确定零件加工中工序能力的等级、估算出合格品或不合品率，针对工艺能力差者予以适当改进能有效提升产品的生产效率。分布图分析法的缺点在于：不能反映误差的变化趋势。加工中，由于随机性误差和系统性误差同时存在，在没有考虑到工件加工先后顺序的情况下，很难把随机性误差和变值系统性误差区分开来。由于在一批工件加工结束后，才能得出尺寸分布情况，因而不能在加工过程中起到及时控制质量的作用。