基于流型的矩形小通道内冷凝传热模型研究
严 彦, 董继先, 高秀峰
(1. 西安工程大学 机电工程学院, 陕西 西安 710049; 2. 陕西科技大学 机电工程学院, 陕西 西安 710021;3. 西安交通大学 化学工程与技术学院, 陕西 西安 710048)
1 前 言
多通道烘缸作为一种新型烘缸结构,较好地改善了传统烘缸由于冷凝水排出不畅导致的干燥效率较低的问题[1-3]。多通道烘缸的干燥过程,即为蒸气在其矩形小通道内冷凝,并通过单侧壁面将所释放热量传递给覆盖在烘缸外表面的湿纸幅的过程。因此,对多通道烘缸传热特性的研究,就是对蒸气在单边换热矩形小通道内的冷凝传热特性的研究。
目前国内外的文献多集中于蒸气在非水平管内或制冷剂在四周换热的圆形通道内的传热特性[4-16],与之相比,现有的对水蒸气在单边换热矩形小通道内的传热特性的研究相当匮乏,仅有美国Argonne National Laboratory[17]、韩国Shin 等[18]及作者[19]对多通道烘缸特殊的冷凝传热情况进行了实验研究。但是由于单边换热矩形小通道内冷凝传热现象的复杂性,仅仅采用实验方法对其进行研究,不仅周期长、费用高,还存在无法揭示其内在规律的缺点。利用数值模拟方法可以弥补实验研究的不足,使得对冷凝传热现象的认识更加深刻。因此,本研究基于作者的实验观测结果,针对所观察到的两相流型分别建立冷凝传热模型。但是,同冷凝传热的实验研究现状一样,现有的数值模拟文献也多集中于制冷剂在圆管内的冷凝两相流模型,鲜见蒸气在矩形通道内冷凝的相关报道。同时,已有文献仅仅将流型简单地分为分层流或环状流,并不足以完整描述事实出现的两相流型。如Cavallini 等[20]提出了一个适用于计算圆形通道内环状流时冷凝传热的无量纲半经验公式。Kosky 等[21]和Traviss 等[22]基于冯卡门速度场分布适用于管内环状流这一假设,开发了计算环状流下冷凝传热系数的程序。Haraguchi 等[23]建立了2 个无因次方程式,分别适用于环状流和分层流等。
有鉴于此,本研究为弥补蒸气在矩形通道内冷凝传热模型的空缺,基于所观察到的流型建立了相应的冷凝传热模型,以期为多通道烘缸的性能优化及设备研发提供参考。
2 矩形通道内冷凝可视化实验
多通道烘缸传热可视化平台系统如图1 所示。蒸气发生器产生的饱和水蒸气经过过热器进入实验段的蒸气通道内,与实验段冷却水通道内的冷却水呈逆向流动并冷凝。蒸气通道与冷却水通道呈背向相对结构,通道示意图如图2 所示。沿实验段长度方向,按图2 中红色线所指方向分别安装7 个热电偶,用以测量蒸气及冷却水的沿程温度变化。蒸气流量及冷却水流量通过涡轮流量计测得,精度为1%。为满足可视化要求,蒸气通道表面由透明的聚碳酸酯树脂制成。实验应用Dimax S4 型高速摄像机对蒸气通道中的气液两相流型进行拍摄。该型号高速摄像机的像素为4 502 fps @ 1 008 × 1 008、分辨率为1279 fps @ 2 016 × 2 016,可以较好地满足实验所需的拍摄清晰度。
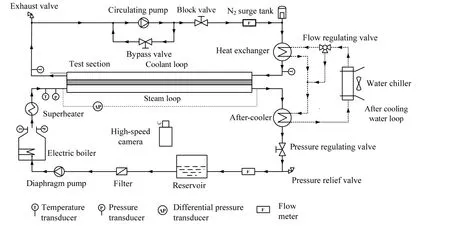
图1 矩形通道冷凝传热可视化平台系统图Fig.1 Schematic diagram of the visualization platform for rectangular tube condensation heat transfer tests
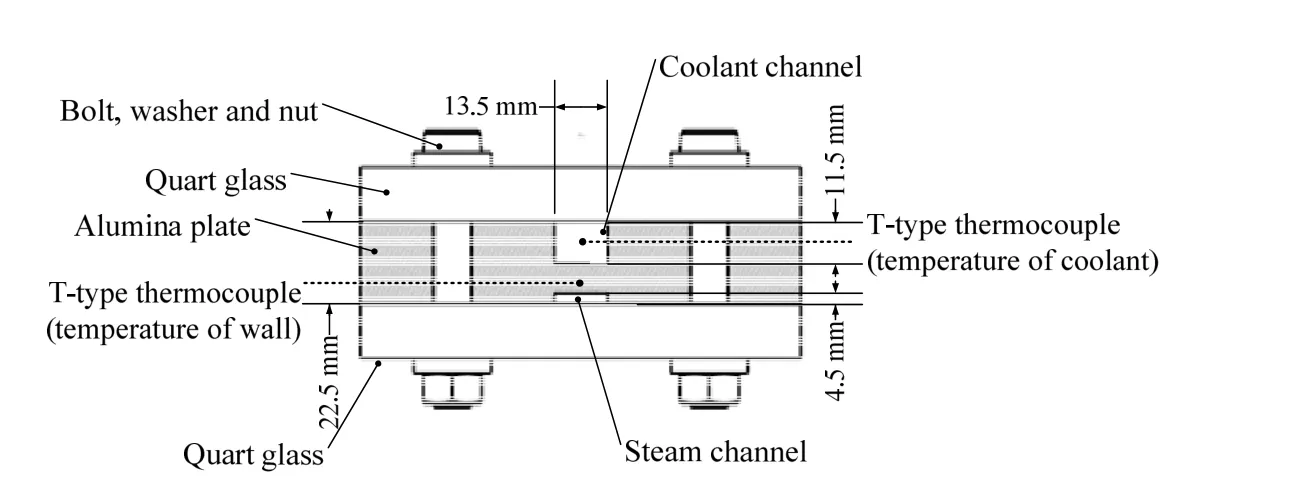
图2 实验段通道结构示意图Fig.2 Schematic diagram of the experimental tube
图3 为实验观测到的蒸气冷凝气液两相流型。在矩形下小通道内主要观察到了环状流、环波状流、波状流、弹状流、塞状流及分层流,实验所拍摄的流型照片如图3 所示。

图3 实验所观察到的各种流型Fig.3 Flow patterns observed in experiments
本研究基于所观察到的蒸气冷凝气液两相流型,建立了矩形通道内蒸气冷凝换热模型。
3 基于流型的冷凝换热模型
不同的气液两相流型具有不同的换热机理,因此,在本节中将蒸气在多通道烘缸内的冷凝传热过程按两相流型分类,建立了基于不同流型的冷凝换热模型。实验中观察到了多种流型,为简化模型,将流型按相似性进行分类。因环波状流及波状流的换热机理相似[24],在本研究中认为它们均属于波状流下的冷凝换热模型;弹状流、塞状流及分层流的换热机理相似[24],则认为它们均属于分层流下的冷凝换热模型。
当流型处于环状流时,此时蒸气在通道中心处快速流动,通道内壁处覆盖有一层薄液膜,由于重力等多种因素的综合影响,冷凝液膜的厚度不可能完全相同。为了简化模型,认为当流型处于环状流时,其内部的冷凝液膜均匀地覆盖在通道内部,液膜厚度处处相等,处于轴对称状态,如图4(a)所示。当流型处于分层流时,冷凝液大多集中在通道下部,且冷凝液膜较厚,形成液池。由于蒸气剪切力及液膜波动等关系的作用,冷凝液表面会出现左右高低不一致的状态,为了简化模型,认为在通道截面处,液池表面平稳无波动,如图4(b)所示。当流型处于波状流时,冷凝液同样会在通道底部形成液池,但液池厚度小于分层流时的液池厚度。波动流时气液相界面间会产生波动,为简化模型,处理方式同分层流,认为在通道截面处,液池表面平稳无波动,如图4(c)所示。
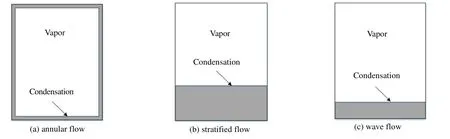
图4 通道内流型示意图Fig.4 Schematic diagram of flow patterns in channels
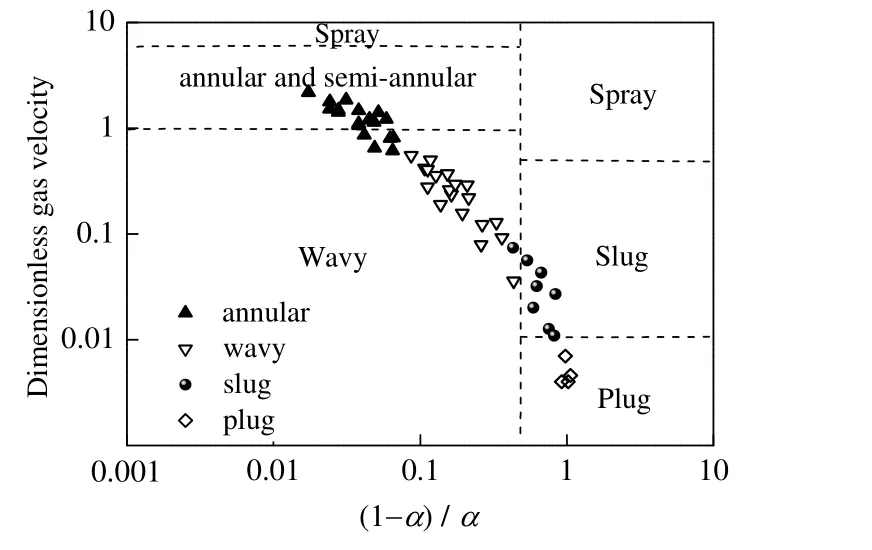
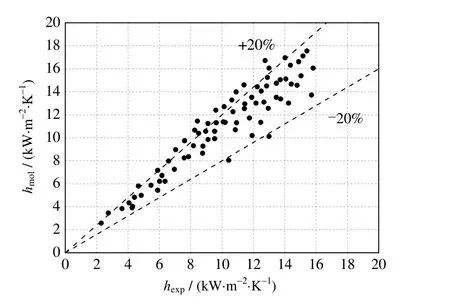
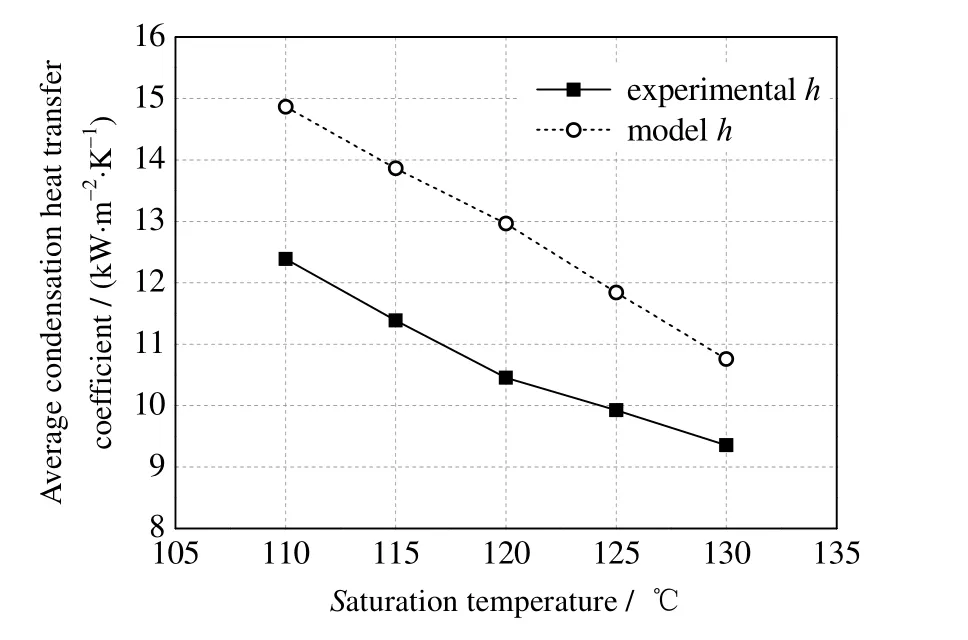
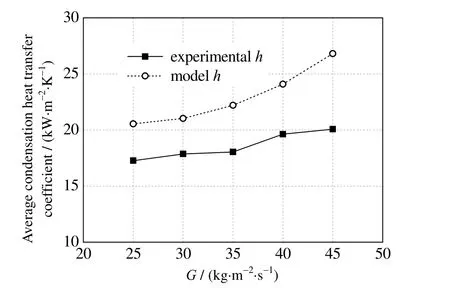
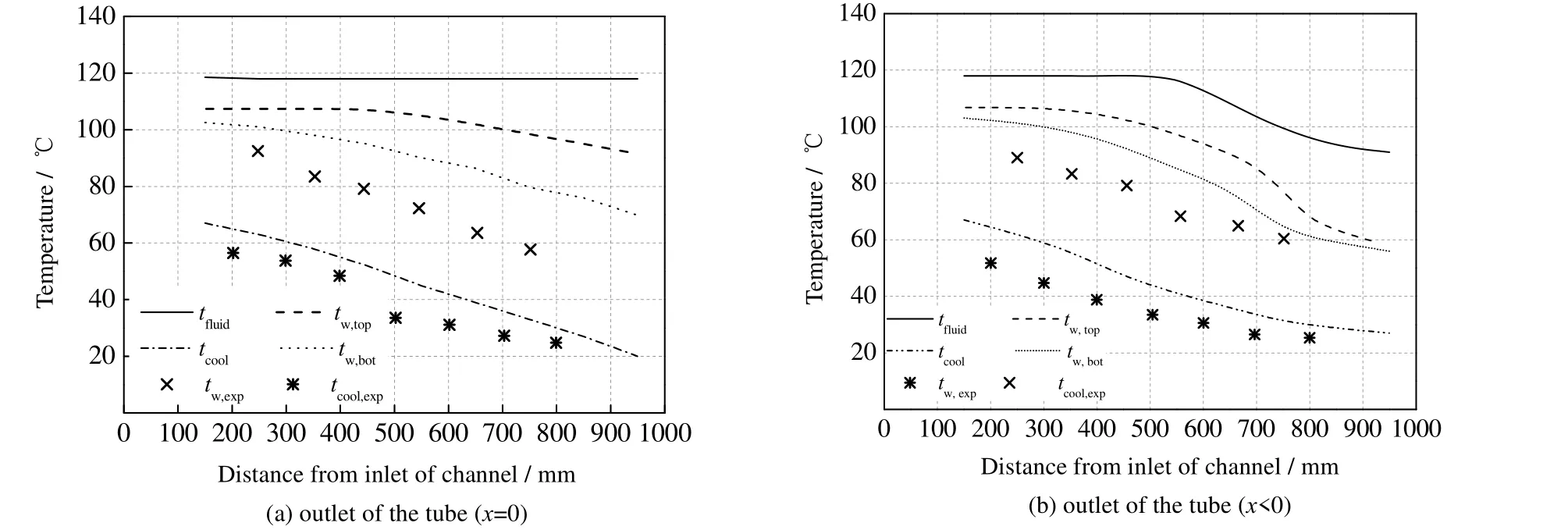
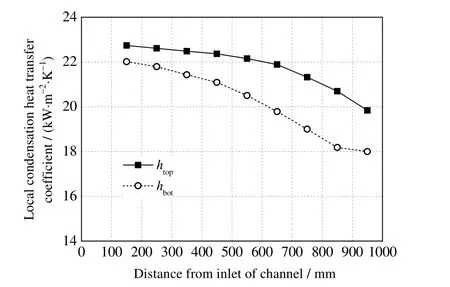
为保证不同流型模型间的连续性,定义了参数l为通道内被膜状凝结所覆盖部分的长度(m)。蒸气在多通道烘缸矩形通道内的冷凝传热通用模型如图4 所示。冷凝初期,蒸气会在通道上壁面形成液膜,随着冷凝过程的进行,冷凝液膜逐渐增厚,在重力作用下沿通道内壁面向下流动,通道下部冷凝液膜逐渐增厚。此时,根据传热机理的不同,通道内的冷凝传热类型可分为膜状凝结传热及对流传热。当流型为环状流时,对应的l=0,通道内的冷凝传热模式为对流传热。当流型为分层流时,对应的l=lstrat,通道上部的冷凝传热模式为膜状凝结换热,通道下部液池的冷凝传热模式为对流传热。当流型为波状流时,此时0 图5 通道冷凝通用模型Fig.5 General model of steam condensation processes 式中:hf为膜状凝结传热系数,W·m-2·K-1;hc为对流传热系数,W·m-2·K-1;a为通道高度,m;b为通道宽度,m。分层流时的lstrat可由式(2)计算得出: 其中φL为冷凝液的体积分数,可由式计算得出: 式中:A为通道截面积,m2。α为蒸气空隙率。 流型从环状流转为波状流(wave)及波状流转为分层流(strat)的分界是由Gwave及Gstrat决定的。即当蒸气质量流速G>Gwave时,流型为环状流,此时l=0。当蒸气质量流速G 通过对单边换热矩形通道进行可视化实验研究,将实验所测得的两相流的流型实验数据与多种流型图进行了对比。结果显示,实验流型观测值与Tandon 流型图[25]较为吻合,如图6 所示。因此,本研究选用Tandon 流型图中的流型转换边界Gwave和Gstrat。 图6 实验值与Tandon 流型图的对比Fig.6 Comparison of experimental data and Tandon flow pattern 对流换热壁面的传热系数hc可由式(5)计算: 式中:Re为液体雷诺数;Pr为液体普朗特数;λ为热导率,W·m-1·K-1;δ为对流换热时积聚在通道下部的液膜厚度,m。 式中:x为干度,μL为液体的动力黏度,Pa·s;cp为比定压热容。 对于式(5)中的参数ξ、m及n,通过实验得到单边换热矩形通道内的冷凝传热系数数据,采用待定系数法求得适用于本模型的参数值,ξ=0.004,m=0.698,n=0.543。 膜状凝结壁面的传热系数hf的表达式可由实验得出。在作者已发表的文章中[26],已将实验数据与常用的一些经验关联式做过对比,发现Shah 关联式[27]所预测的冷凝传热系数值在环状流方面与实验数据较为吻合,因此选取Shah 的关联式作为膜状凝结的传热系数表达式,如式(9)所示: 综上所述,本研究所建立的基于两相流型的分布参数冷凝传热模型的应用方法如下: (1) 在每个微元段的入口处,根据入口焓值的不同,流体可能处于过热状态、气液两相状态或者过冷状态。当微元段入口焓值大于饱和蒸气焓时,此时流体处于单相的过热蒸气状态,选取管内过热蒸气的对流换热公式来计算此时的传热系数,其表达式为 式中:Dh为管道水力直径,m。 (2) 当微元段入口焓值小于饱和液体焓时,此时流体处于单相的过冷水状态,可选取管内过冷流体的对流换热公式来计算此时的传热系数,其表达式为 (3) 当微元段的入口焓值介于饱和蒸气和饱和液体焓之间时,此时通道处于气液两相流状态。在此种情况下,首先需要通过Mandhane 经验流型图来判断通道中的流型种类,是属于环状流、环波状流、波状流、弹状流、塞状流及分层流; 如果流型为环状流,此时l=0,由式(1)可知hpa=hc,hc由式(5)计算得出,δ由式(6)计算得出。如果流型为环波状流及波状流,按简化模型认为此时流型属于波状流。lstrat由式(2)计算得出,l由式(4)计算得出。hc和hf分别由式(5)和式(9)计算得出,最终hpa由式(1)计算得出。如果流型为弹状流、塞状流及分层流,按简化模型认为此时流型属于分层流。lstrat由式(2)计算得出。hc和hf分别由式(5)和式(9)计算得出,最终hpa由式(1)计算得出。 为了验证本研究所建立的基于两相流型的蒸气冷凝传热模型的准确性,文中所建立的通道模型与实验研究中所用通道尺寸保持一致,蒸气通道长、宽、高分别为1 020、13.5、4.5 mm,冷却剂通道长、宽、高分别为960、13.5、15.5 mm。将作者已做的实验结果[26]与模型的理论计算结果进行对比,验证了模型的准确性后,应用模型对单边换热矩形小通道内的蒸气冷凝传热特性进行分析。 为验证本研究所建立的冷凝传热模型的有效性,将模拟计算与实验所得的冷凝传热系数进行对比,结果如图7 所示,图中hexp为冷凝结热系数实验值,hmol为冷凝传热系数模型计算值。从图中可以看出,两者的偏差基本维持在-20% 到20% 内,说明所建立的模型较为准确。从图中还可以看出,误差基本为正值,即模型计算出的冷凝传热系数略微大于实验测量值,这是因为本研究所建立的传热模型将实验中观察到的7 种流型归纳为3 种,将一些冷凝液膜较厚的流型划为冷凝液膜较薄的流型中,如将环波状流划为环状流,弹状流、塞状流划为分层流。同时,在建立模型时采用了拟合的传热关联式,也会造成误差的产生。 图7 冷凝传热系数实验值与模型计算值的对比Fig.7 Comparison of experimental and model values of condensation heat transfer coefficients 图8 为蒸气饱和温度对平均冷凝换热系数的影响。从图8 中可以看出,随着蒸气饱和温度的升高,模型预测的冷凝传热系数降低,模拟结果与实验研究具有相同的规律。蒸气饱和温度的增加使得其与通道壁面间的换热温差增大,加速了蒸气凝结速率,使得冷凝液膜变厚,热阻增加,导致平均冷凝传热系数下降。从图中还可以看出,由于模型将液膜较厚的流型归为液膜较薄的流型中,因此蒸气冷凝传热系数的模型预测值略大于实验所测得的冷凝传热系数。 图8 饱和温度对平均冷凝传热系数的影响Fig.8 Effects of saturation temperature on average condensation heat transfer coefficients 图9 为蒸气质量流速G对平均冷凝换热系数的影响。从图中可以看出,随着蒸气质量流速的升高,模型预测的冷凝传热系数增大,且从图中还可以看出,当蒸气质量流速较大时,冷凝传热系数的增加率略高于蒸气质量流速较小时的增加率。这是因为当蒸气质量流速较大时,通道内的流型大部分为环状流,此时蒸气质量流速为影响传热系数的主要因素;当蒸气质量流速较小时,通道内的流型大部分为分层流,此时蒸气与壁面的温差为影响传热系数的主要因素,蒸气质量流速的影响减弱。 图9 蒸气质量流速对平均冷凝传热系数的影响Fig.9 Effects of mass flux on average condensation heat transfer coefficients 在多通道烘缸出口处,当蒸气焓值大于饱和液体焓时,说明此时蒸气还未完全冷凝,本该用于干燥湿纸页的显热被排放,造成蒸气能源的浪费;当蒸气出口焓值低于饱和液体焓时,说明饱和蒸气在未到通道出口就已完全冷凝,通道内存在过冷段,传热效率会大大降低;而当蒸气出口焓等于饱和液体焓时,说明在通道出口处,饱和蒸气中的潜热完全释放出来,热量全部用于湿纸页的干燥,认为此时处于多通道烘缸干燥的最优状态。 当蒸气饱和温度为120 ℃时,如图10 所示为当蒸气的出口干度等于0(G=40 kg·m-2·s-1)及出口干度小于0(G=30 kg·m-2·s-1)时,沿通道轴向的分布规律,图中tfluid为流体温度、tcool为冷却剂温度、tw,top,tw,bottw,exp分别为冷却剂通道上表面温度及下表面温度为实验测得的壁面温度,tcool,exp为实验测得的冷却剂温度。从图中可以看出,模型计算所得到的温度分布趋势与实验测得的温度的变化趋势基本相同,即:通道内气液两相流体的温度值最高,且沿着流体流动方向逐渐降低;壁面温度小于流体温度,沿着流体流动方向也逐渐降低。由于实验及模拟中均设定蒸气与冷却剂逆向流动,因此沿流体流动方向,冷却剂温度逐渐降低。 图10 温度沿通道轴向的分布Fig.10 Profiles of temperature distribution along the channel 而由于通道内气液两相流型不同,各处的温度参数在不同流型时具有不同特点。在通道前端,即蒸气刚进入通道时,此时通道内流型为环状流,此流型下的通道上下壁面处的温度较为接近;而通道后端,此时通道内的气液两相流型逐渐转换为波状流或分层流,通道上下壁面的温度产生了一定的差异,且下壁面的温度低于上壁面的温度。这是由不同流型的冷凝模式不同所引起的:当流型为环状流时,冷凝模式为轴对称模式;当流型为分层流时,通道下部的冷凝模式为强制对流冷凝,而通道上部的冷凝模式为膜状冷凝,冷凝液膜堆积在下壁面,使得壁面温度较低。从图中还可以看出,在通道后半段,即通道内两相流型为分层流时,其壁面温度的变化趋势较通道前半段平缓,这是因为流型为分层流时,其液膜的波动情况比环状流时平缓。而从图10 (b)中可以看出,当通道出口蒸气干度小于0 时,由于通道后部产生了一定长度的过冷段,此时流体温度及壁面温度基本不变且温度值均较低。 从图10 中还可以看出,相比于未优化的多通道烘缸中可能存在的过冷段,多通道烘缸处于最优设计状态时,各参数的温度分布均较为平稳,烘缸壁面温差较小,保证了烘缸干燥纸张时干燥温度的一致性。 由3.4 节可知,当蒸气饱和温度为120 ℃,G为40 kg·m-2·s-1时,多通道烘缸处于最优状态。图11为在此状态下,通道内局部冷凝传热系数沿通道轴向的分布规律。从图中可以看出,通道入口处流型处于环状流,因此上下壁面处的冷凝传热系数相差不大。随着冷凝过程的进行,流型进入波状流和分层流,通道上壁面的冷凝模式为膜状凝结换热,冷凝液膜厚度较小,而通道下壁面处的冷凝液膜沿流体流动方向逐渐增厚,形成液池,导致液膜导热热阻较大,因此上下壁面间的冷凝传热系数差值逐渐增大。在分层流后期,冷凝液池增加速度减缓,因此下壁面处的冷凝传热系数下降幅度也随之减小。从图中还可看出,当多通道烘缸处于最优设计状态时,冷凝传热系数较高且波动较小,保证了多通道烘缸干燥纸张时的稳定性和高效性。 图11 局部冷凝传热系数沿通道轴向的分布Fig.11 Distribution of local condensation heat transfer coefficients along the channel 本研究以蒸气在单边换热的矩形小通道内的两相流型可视化实验为基础,提出了一种基于两相流型的水平矩形通道内冷凝传热模型,得到结论如下: (1) 与以往传热模型相比,本研究所建立的冷凝传热模型采用的经验参数较少,从一定程度上可以减少过多应用经验参数所带来的误差,提高模型的准确性。 (2) 模型可较准确地预测流型处于环状流、环波状流、波状流、弹状流、塞状流及分层流时的冷凝传热特性,且模型预测值稍大于实验值。 (3) 蒸气饱和温度的降低及质量流速的升高均会使平均冷凝传热系数增大,同时蒸气质量流速较大时的冷凝传热系数的增量略大于质量流速较小时。 当流型处于环状流时,由于通道内壁面的冷凝液膜厚度基本相同,通道上下壁面处的温度及局部冷凝传热系数较为接近;随着流型逐渐发展为分层流时,由于通道下壁面处的液池厚度大于上壁面处的液膜厚度,因此通道上壁面温度及局部冷凝传热系数均大于下壁面;在分层流后期,由于液池厚度增速变缓,因此上下壁面处的差值也逐渐减小。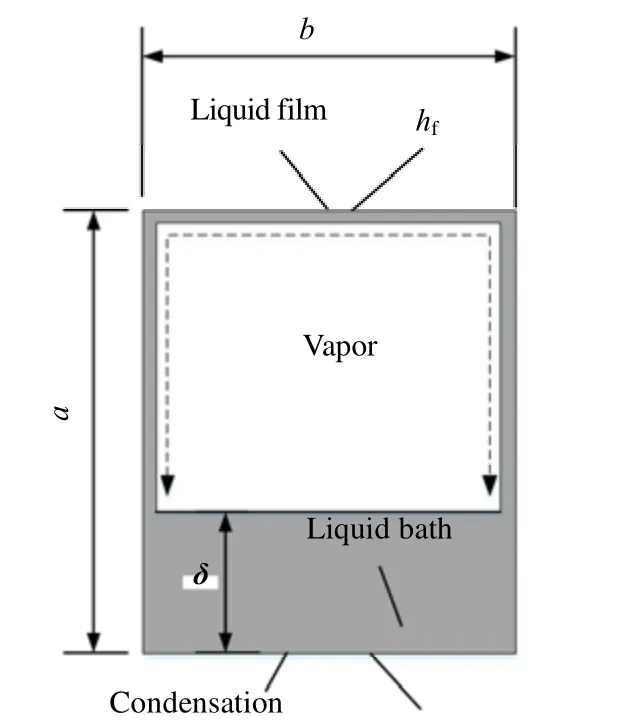

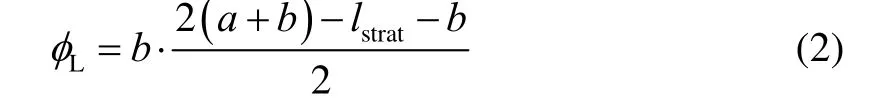
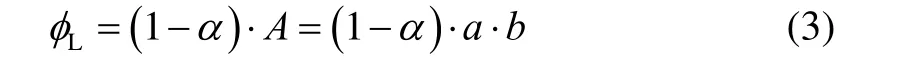
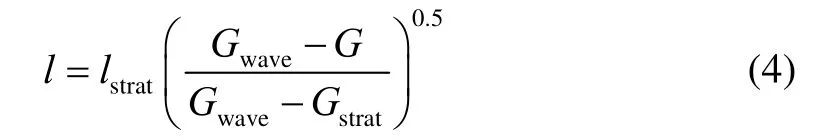





4 模拟结果分析
4.1 模型有效性验证
4.2 蒸气饱和温度对平均冷凝传热系数的影响
4.3 蒸气质量流速对平均冷凝传热系数的影响
4.4 温度沿通道轴向变化
4.5 局部冷凝传热系数沿通道轴向变化
5 结 论

