基于干扰观测器的非奇异快速终端滑模控制方法

(1.广西大学 机械工程学院, 广西 南宁 530004；2.南宁正腾农机有限公司, 广西 南宁 530007)

0 引言

近些年,滑模控制作为解决不确定非线性系统控制问题的有效方法，已经广泛应用于航空航天、机械臂轨迹跟踪控制、桥式吊车等领域[1-3]。

机械臂是一种高度复杂、强耦合的不确定非线性系统，对这种难以建立精确数学模型的系统，很难寻找一种合适的实时鲁棒控制方法。滑模控制是一种有效的非线性控制策略，具有鲁棒性强、无需精确模型、对参数摄动不敏感、抗干扰能力强、响应速度快等优点，特别适合于机械臂系统控制。然而，滑模控制容易引起系统控制输入振动的特点使其应用受到限制[4]。因此，针对抖振削弱的研究一直是滑模控制领域研究的重难点。

抖振问题吸引了一大批国内外学者投入研究并取得了丰富成果[5-7]。VAN等[8]把积分非奇异快速终端滑模控制和反演设计思想结合起来，设计了一种自适应反演非奇异快速终端滑模控制器(ABNFTSMC)。该控制器实现了有限时间收敛且无奇异问题。不仅削弱抖振，相比其他方法如计算力矩、PID等具有更好的轨迹追踪精度；WANG等[9]设计的控制器结合了模糊滑模控制和RBF神经网络控制思想，该方法分别利用RBF神经网络和模糊控制逼近滑模控制律的等效控制项和切换控制项，削弱了抖振；徐传忠等[10]把滑模控制和反演设计方法结合设计控制器，利用RBF神经网络去估计不确定因素上界，实现了抖振削弱；李爱民等[11]通过改进粒子群算法优化了模糊隶属函数的参数，进而提高了模糊滑模控制器的性能；张爱林[12]利用和声搜索算法优化了RBF神经网络参数，进而提高了神经滑模控制器对系统模型的逼近能力，不仅实现了无模型控制，还削弱了系统抖振。

为实现机械臂对目标轨迹的高精度轨迹跟踪控制，在考虑机械臂动力学模型建模误差、关节摩擦和外界干扰的共同作用下，本文提出了一种基于非线性干扰观测器的非奇异快速终端滑模控制方法。该方法首先结合了传统的快速终端滑模控制和非奇异终端滑模控制，不仅可以使跟踪误差在有限时间快速收敛至零且对机械臂建模误差和外界干扰具有较强鲁棒性。其次，针对该方法控制输入抖振严重的问题，通过引入非线性干扰观测器技术对系统不确定性进行估计、控制律补偿且引入边界层概念的方法以降低滑模控制的抖振现象。

本文最后在Matlab/Simulink环境下进行了以三自由度机械臂为研究对象的对比仿真实验，其结果表明了所得结论的正确性和有效性。

1 机械臂动力学描述

被控对象是多关节机械臂，动力学方程为

(1)

图1 空间三自由度机械臂结构Fig.1 Structure of spatial 3-DOF manipulator

G(q)=G0(q)+ΔG(q)，

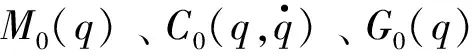
(2)

(3)

式中，d代表所有建模误差及外界干扰的总合。本文选择空间三自由度机械臂为研究对象，其结构如图1所示。

公式(2)中：

h11=I1+a1cos2(q2)+a2cos2(q2+q3)+2a3cos(q2)cos(q2+q3),

h12=h21=h13=h31=0,h22=I2+a1+a2+2a3cos(q3),

h23=h32=a2+a3cos(q3),h33=I3+a2,

g2=b1cos(q2)+b2cos(q2+q3),g3=b2cos(q2+q3),

式中，q1、q2和q3分别为空间三自由度机械臂各关节的角位移，其余各项取值见表1。

表1 动力学参数值Tab.1 Values of kinetic parameters

2 控制器设计

控制器的设计分为：①确定非奇异快速终端滑模面。根据Lyapunov理论设计控制律。②针对图1的机械臂模型设计非线性干扰观测器对模型不确定项和外界干扰给予补偿，控制系统结构框图如图2所示。

图2 控制系统结构框图Fig.2 Block diagram of control system

2.1 非奇异快速终端滑模控制器设计

本文选择非奇异快速终端滑模面[13]：

(4)

式中，α、β、γ>0为设计常数;p、q为正奇数且满足：1

当系统到达滑模面(s=0)并处于滑动模态时，系统状态在任意初始条件下渐进收敛至零。

证明如下：

取s=0，此时，式(4)为

由滑模面参数可得，D≤0且D≡0时，e≡0，根据LaSalle不变集原理，当t→∞时，e→0，即系统状态随时间而衰减至零，证毕。

所设计的滑模控制器的控制目标是使关节实际轨迹准确追踪理想轨迹，滑模趋近律选择指数趋近律：

(5)

τ=τeq+τsw

(6)

式中，τeq、τsw分别代表了滑模控制律中的等效控制项和切换控制项。

2.2 非线性干扰观测器设计与收敛性分析

针对式(2)的机械臂动力学模型，结合其惯性矩阵具有普遍性特点，非线性干扰观测器设计为

(7)

L(θ)=X-1J-1(θ),

(8)

(9)

干扰跟踪的收敛性证明：

设Lyapunov函数为[14]

(10)

(11)

现构造不等式

(12)

其中：ϑ>0为对称正定阵。则存在ϑ*>0，使得

若确定合适的观测器增益矩阵X，满足式(12)，则由Lyapunov原理可知本文设计的干扰观测器对不确定项跟踪误差指数收敛。

2.3 LMI不等式的求解

由于式(12)含有非线性项，必须将其转化为线性矩阵不等式(LMI)进行求解。由Schur补定理[15]可知，式(12)与下式等价，即通过对下式矩阵不等式的求解，可以得到使观测器收敛的增益矩阵X。

X=0.0012diag(1,1,1)。

2.4 控制系统稳定性分析

在引入非线性干扰观测器后，滑模控制律为

(13)

考虑由式(2)表示的机械臂系统，如果采用式(6)的控制律和式(7)的干扰观测器，输出轨迹跟踪误差在有限时间收敛且系统具有稳定性。

设Lyapunov函数：

(14)

对V2求导，并代入式(11)、(13)整理可得

为了进一步减小抖振现象，本文引入边界层概念，即在控制律的切换项中用饱和函数sats代替传统的符号函数sgns。饱和函数sats[16]为

(15)

3 仿真实验

3.1 仿真实验设计

① 被控系统动力学方程见式(2)。

② 本文理想跟踪轨迹为q1d=q2d=q3d=1.2sint，初始状态为[0,0,0,0,0,0]。为了便于比较控制算法的优劣，设置3种方法的对比研究，分别是文献[17]的线性滑模控制方法[17]、非奇异快速终端滑模控制方法(简称终端滑模)及本文提出的基于非线性干扰观测器的非奇异快速终端滑模控制方法,其中文献[17]的控制算法为

(16)

为进行仿真比较研究，控制器共同参数选为：α=3;β=5;γ=0.5;p=9;q=5;ε=diag(20,130,20);k=10;Δ=0.5;c=diag(1,1,1)。

3.2 仿真结果分析

仿真结果如图3至图5所示。图3和图5为在本文设计控制算法下各关节的轨迹跟踪误差和控制力矩；图4为观测器对系统不确定性的干扰观测图；表2和表3给出了各算法的均方差和稳态误差。从仿真结果可知，3种控制方法均实现了机械臂关节轨迹跟踪高精度控制，经比较分析可得如下结论：

① 在跟踪误差方面，从图3可以看出，3种控制方法的轨迹跟踪误差在系统存在建模误差、关节摩擦及外界干扰情况下均无大的变化，表明三者具有较强的鲁棒性；终端滑模控制较线性滑膜控制极大地提高了收敛速度，体现出终端滑模的有限时间收敛特性。本文算法在此基础上进一步提高了机械臂轨迹跟踪时各关节的收敛速度，更快地使跟踪误差收敛至零，且关节1和关节2的最大跟踪误差较终端滑模控制方法更小，关节3的最大跟踪误差与终端滑模控制方法相近，表明本文所提控制方法能够有效提高跟踪精度。均方差是衡量控制系统平均跟踪精度的有效方法，其和稳态误差分析方法被广泛应用于各类控制系统控制性能比较中[18-19]。由表2可以看出终端滑模和本文算法控制下关节1和关节2的均方差比线性滑模控制方法的均方差降低了89.6%、82.4%和97.9%、76.1%；由表3可知，在线性滑模、终端滑模和本文算法的控制下关节3的跟踪误差稳态值分别为-0.002 2 rad、小于0.000 1 rad和小于0.000 1 rad。虽然在终端滑模和本文算法控制下机械臂很快地实现了跟踪误差收敛且具有很高的精度，但其均方差是略高于线性滑模控制的，这是因为前期跟踪误差过大导致了较大的误差积累。

② 在对不确定性的跟踪方面，从图4可以看出，本文所设计的干扰观测器以较高的精度实现了对机械臂系统不确定项的有效逼近。

③ 在控制力矩方面，从图5可以看出，3种控制方法都存在抖振现象。终端滑模控制方法较线性滑模虽然明显提高了跟踪精度，但抖振现象仍然十分严重。本文算法利用一种非线性干扰观测器对系统不确定性进行估计，并在控制律中补偿以削弱不确定性影响。由图5(c)可以看出，本文算法不仅提高了终端滑模良好的轨迹跟踪控制性能，且有效地削弱了抖振现象。

图3 关节轨迹跟踪误差图Fig.3 Joint trajectory tracking error diagram

图4 各关节不确定跟踪图Fig.4 Tracking chart of joint uncertainty

表2 均方差Tab.2 Mean square error单位：rad

表3 稳态误差Tab.3 Steady-state error 单位：rad

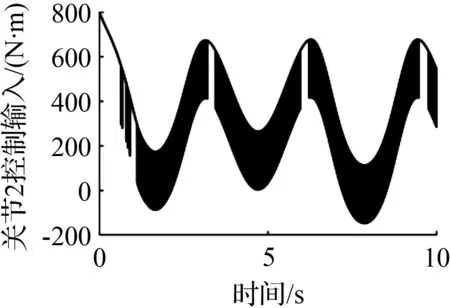
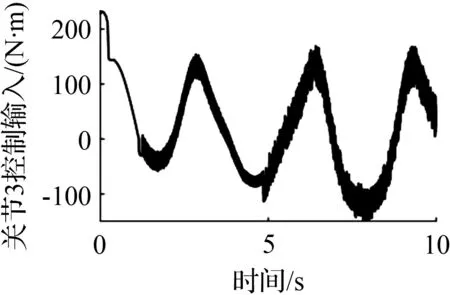
(a) 线性滑模控制各关节输入

(b) 终端滑模控制各关节输入

(c) 本文算法控制各关节输入

4 结语

① 滑模控制领域普遍采用较简单的二自由度机械臂为研究对象，没有考虑到实际应用中机械臂是多自由度的这一特点。所以，针对多关节机器人系统，本文建立了复杂空间三自由度机械臂动力学模型。

② 本文以三自由度机械臂为控制对象，在考虑建模误差、关节摩擦和外界干扰等条件下提出了一种机械臂非奇异快速终端滑模控制方法。该方法采用最新的非奇异快速终端滑模面且结合指数趋近律进行控制律设计。不仅实现了轨迹跟踪误差的有限时间收敛，而且控制系统具有良好的误差收敛快速性、稳定性和鲁棒性。

③ 为了解决所设计的非奇异快速终端滑模控制方法控制输入抖振严重的问题，本文使用非线性干扰观测器对系统不确定性进行估计和抑制并结合饱和函数替代控制律符号函数的方法，有效削弱了抖振现象。

④ 在Matlab/Simulink环境下通过三组对比实验下机械臂关节控制输入、轨迹跟踪等性能的比较，仿真结果表明本文算法在保证了终端滑模的优良控制效果的前提下，有效削弱了抖振。终端滑模和本文算法控制下关节1和关节2的均方差比线性滑模控制方法的均方差分别降低了89.6%、82.4%和97.9%、76.1%，虽然关节3的均方差由于初始误差积累较大于线性滑模控制，但其误差快速收敛且在收敛后稳态误差小于0.000 1 rad，远低于线性滑模控制的-0.002 2 rad。这证明了本文所得结论的正确性和有效性。