基于改进磁链位置判断方法的直接转矩调速系统

李 春，张 栋，王东伟，王冠柯

（上海电机学院 机械学院，上海201306）

直接转矩控制（Direct Torque Control，DTC）技术本质上属于矢量控制技术，相比基于转子磁链定向的方案，其在很大程度上解决了矢量控制中计算复杂、特性易受电动机转子参数变化影响的缺点。20世纪80年代，Depenbrock［1］提出了异步电动机直接自控制（Direct Self Control，DSC）的控制方案。同时期Takahashi等［2］也提出了基于空间矢量的圆形磁场DTC方案，将定子磁场划分为6个扇区，在每个扇区内分别查表选择对应的电压矢量，最终形成闭合的磁链轨迹，以获得更快的扭矩响应和更高的效率。随后，DTC方案不断地完善和改进，主要集中在控制转矩脉动［3］、无速度传感器控制［4］、模糊参数观测及智能控制［5］等方面，相关技术理论已较为成熟。

周道龙等［6］利用定子磁链的幅值和角度判断磁链所在扇区，并编写了Matlab中的S函数来实现。王斌等［7］针对永磁同步电动机DTC中存在磁链和转矩脉动大、逆变器开关频率不恒定的缺点，提出了一种无差拍的控制方案：在一个控制周期内，补偿给定磁链与实际磁链的幅值误差，同时补偿给定转矩与实际转矩的幅值误差，并构造定子磁链降阶观测器，实现了磁链和转矩的无差拍控制，使整个系统实现无速度传感器运行。刘洋等［8］针对异步电动机定子电阻存在压降，导致传统6扇区DTC所选电压矢量在扇区交界处可能失效的问题，提出一种适用于高采样频率的新型电压和电流模型的观测器，建立了定子磁链观测值与真实值的频率响应方程，并通过采用12扇区切换的方法有效提高了系统控制的可靠性。廖永衡等［9］设计了一种基于滑模控制理论的定子磁链自适应滑模观测器，以定子电流和磁链为状态变量，利用实际电流和观测电流的误差构成滑模面，将状态开关信号输入到电流、磁链状态方程，对电流、磁链观测进行校正，减小了系统平均转矩脉动。纪泽宇等［10］针对磁链估计方法在DTC方面的不足，从DTC的基本原理和感应电动机的多变量数学模型入手，对磁链观测器进行了优化。

DTC的定子磁链观测和扇区判断是正确选择电压空间矢量的前提。在定子磁链观测方面，大多数文献均利用定子磁链的幅值和角度判断其所在扇区的位置［11-13］，但在具体的实施方法上论述较少，且计算量较大，不利于执行机构的高速控制以及DTC的推广运用。因此，本文提出了一种利用定子磁链观测结果判断磁链所在扇区位置的改进方法。该方法直接利用定子磁链幅值在两相坐标轴上的分量判断扇区位置。根据扇区位置选择对应的电压空间矢量，从而实现异步电动机的DTC。通过Matlab仿真分析，相比传统利用定子磁链的幅值和角度判断的方法，该方法在原理上更简单，在算法上更简洁，有利于降低控制器的性能要求，提高系统响应速度和降低成本。

1 改进的磁链位置判定方法

DTC系统的重点在于观测定子参数，即判定定子磁链矢量的空间位置。存在多种判断定子磁链位置的判断方法，例如利用定子磁链ψs的角度θψs来判断其位置，或利用ψs在α、β轴上投影的比进行判断［3］。在Matlab仿真中，投影比值的分母ψsα不能为零，否则容易造成电动机定子磁链无法起动，仿真失效。因此，本文提出了一种改进方法，即直接采用定子磁链在α、β上的分量ψsα、ψsβ进行判断。根据电压模型法，系统检测三相定子电压和电流，经3 S/2 S变换得到在αβ静止坐标系下的两相电压（usα，usβ）和电流（isα，isβ）。由定子电压方程可得定子磁链ψs在αβ坐标系上的分量：

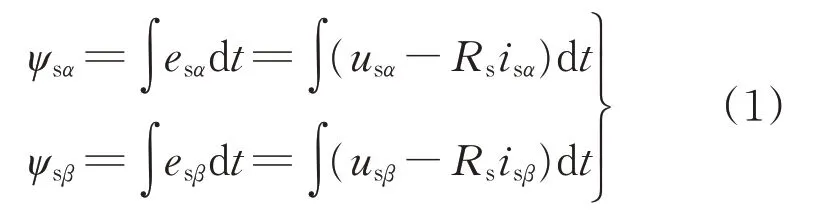
式中：Rs为定子绕组电阻；esα、esβ为两相坐标轴下的定子绕组电动势。

在得到定子磁链分量之后，还需对定子磁链运行空间划分扇区。参考Takahashi等［2］的扇区划分方法，可将磁链圆划分为6个扇区，划分原则为

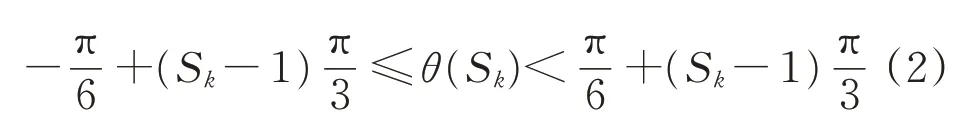
式中：Sk为扇区号，Sk取1~6，即可将圆形磁场划分为6个扇区，每个扇区60°；θ为扇区角度。

以给定励磁|ψs|的大小为磁链圆半径，以为分界点，即可将空间划分为6个扇区，划分情况如图1所示。

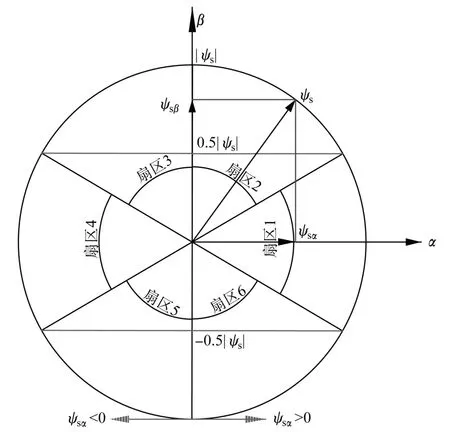
图1 改进的磁链扇区判断方法

由文献［14］可知，电压空间矢量与逆变器的开关状态相对应。如电压空间矢量指向α轴（0°）时，逆变器开关组合SA-SB-SC为100（上桥臂），对应电压空间矢量u4，输出三相电压uA为正，uB和uC为负。其余电压空间矢量的方向如图2所示。

由图2可知，在不同的扇区选择不同的电压空间矢量会对输出定子磁链产生不同的影响。例如定子磁链轨迹位于扇区1且逆时针运行时，选择电压矢量u2会使磁链减小，而选择电压矢量u6会使磁链增加。其余电压空间矢量同理。

结合图1和图2，将ψs投影到α、β坐标上，得到ψsα、ψsβ。ψsβ最大值等于给定励磁|ψs|，由于β轴右边ψsα>0，左边ψsα<0，故扇区位置的判断方法如表1所示。

由表1可知，若某一时刻定子磁链在α轴上的分量ψsα>0，且在β轴上的分量ψsβ<-0.5|ψs|，那么磁链此时位于扇区6。结合图2，磁链在扇区6时，要使电动机逆时针旋转，应选择电压矢量u6或u4，再根据磁链调节指令从这两个电压矢量中选择一个矢量作为最终输出。以此类推，利用该方法可以得到6个正确的扇区位置，并由此选择对应的电压矢量。

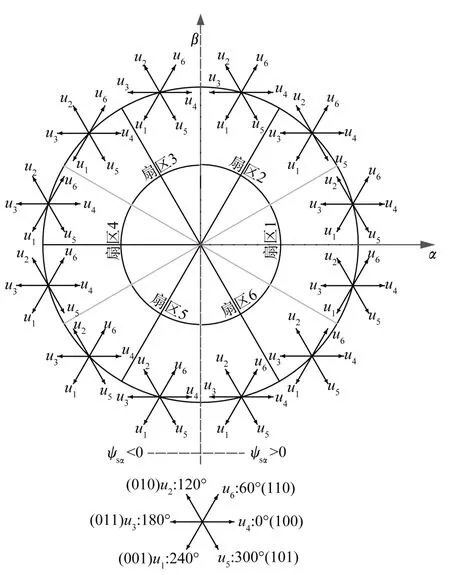
图2 电压空间矢量与磁场扇区的位置关系

表1 改进的扇区位置判断表

2 异步电动机DTC方案

电压空间矢量对应逆变器上桥臂的开关状态。若以SA、SB、SC代表三相桥臂的开关状态，则定义SA、SB和SC=1时，逆变器上桥臂Q1、Q3、Q5接通，下桥臂Q2、Q4、Q6关闭，如图3所示。参考图2，若选择电压矢量u4，则SA=1，SB=0，SC=0，对应上桥臂Q1=1，Q3=0，Q5=0，下桥臂状态相反。

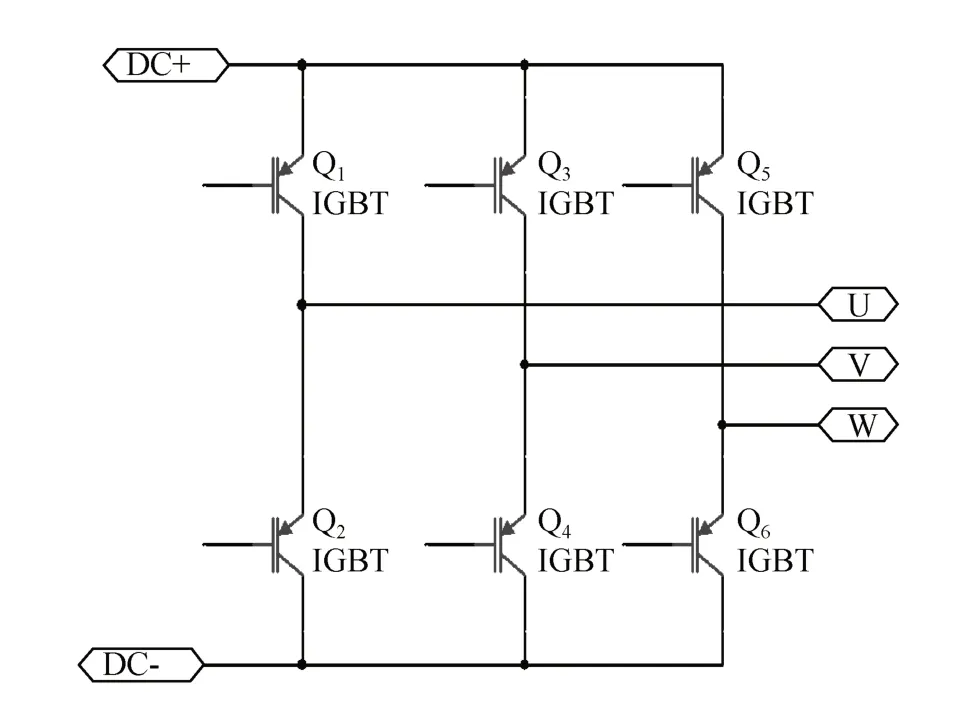
图3 两电平逆变器

由图3可知，在空间以120°对称的三相定子绕组UVW上通入三相对称电压uA、uB、uC，即可在电动机气隙中合成旋转磁场[15]。其大小和空间随时间变化，以矢量us表示。三相定子电压与电压空间矢量的关系由park变换表示为

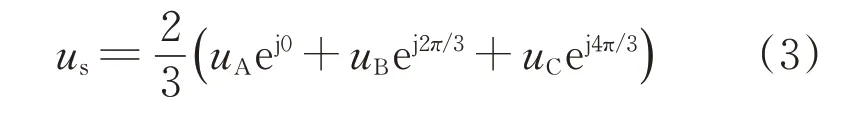
式中：us为定子电压。

绘制异步电动机DTC原理框图[16]如图4所示。该直接转矩系统控制方案包括3S/2S坐标变换、转矩和磁链计算、扇区位置判断算法、磁链调节器、PID转速调节、转向调节、转矩调节和电压空间矢量选择等模块。其中坐标变换和转矩、磁链计算方法属于基础理论，本文不再细述。扇区判断算法参考表1。磁链和转矩调节均采用施密特滞环控制器，设置合适的误差带，将转矩和磁链偏差控制在目标范围内。转向调节通过比较输入转矩和计算转矩的正负来实现，若输入转速为负，则输入转矩T*e为负，与计算转矩作差后为负值，控制转向调节器输出转向控制信号PN=0。

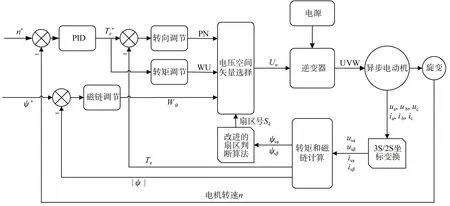
图4 异步电动机DTC原理

利用改进的扇区判断方法得到扇区位置以后，还需根据转向调节信号PN和转矩调节信号WU选择电压矢量。PN=1选择正转的两个电压矢量，PN=0选择反转的两个电压矢量。根据磁链调节信号----Wψ，从两个同向的电压矢量中选择一个电压矢量作为最终的输出。

异步电动机转矩为

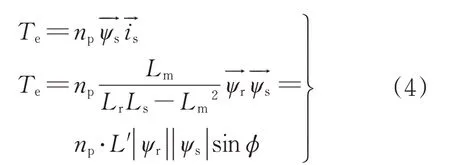
由式（4）可知，异步电动机需要通过插入零矢量的方式来调节定子磁链和转子磁链之间的角度差（转矩角），从而实现电动机转矩大小的调节。可根据转矩调节器输出的WU信号决定是否插入零矢量：WU=1时插入零矢量，使转矩角减小，电动机转矩减小，且插入零矢量时需要观察前一时刻的开关状态，遵照开关次数最少原则，以减少开关损耗；WU=0时不插入零矢量，转矩不会减小。

参考上一章及文献［14］中的相关内容，绘制电压矢量开关选择表如表2所示。

表2 电压矢量开关选择表

表2中，PN为转向控制信号，PN=1时电动机正转，PN=0时电动机反转；WU为转矩控制信号，WU=0时不减小转矩，WU=1时插入零矢量减小转矩；为磁链控制信号，时磁链增加，时磁链减少。由表2可知，系统判断出扇区位置后，再根据转向信号、转矩信号和磁链调节信号，选择最终唯一的电压矢量输出给逆变器，从而实现DTC控制。

3 控制方案的建模仿真与性能分析

按照前两章的原理，搭建改进扇区位置判断方法的DTC系统的Matlab/Simulink仿真模型，并与传统利用定子磁链幅值和角度判断扇区位置的控制方案作对比。设定系统参数如表3所示。

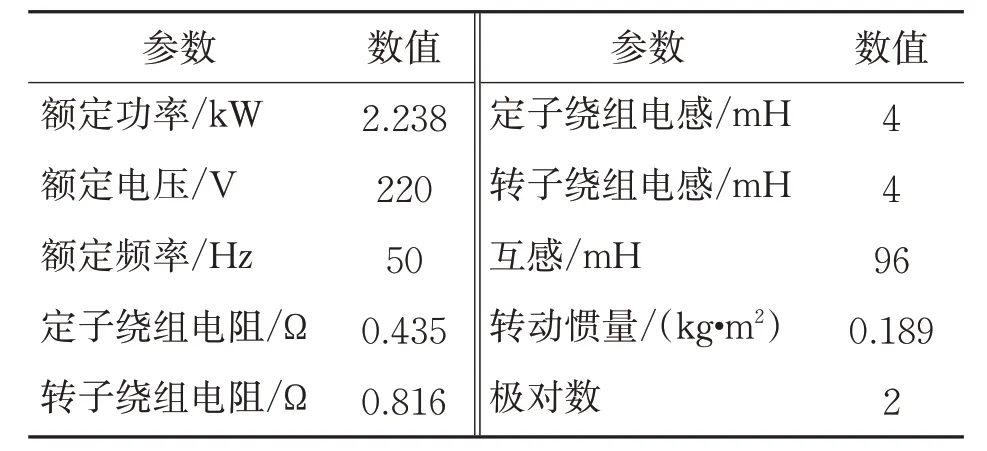
表3 异步电动机参数设定

采用定步长仿真，解算器（solver）选择自动（auto）模式，步长0.000 01，仿真时间2 s。给定初始励磁1 Wb，由

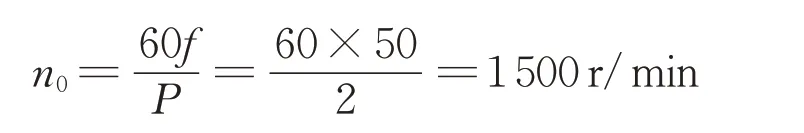
可知该电动机理想转速为1 500 r/min，故设定初始转速为1 500 r/min。设定转矩调节器滞环宽度为0.5 Nm，磁链调节器滞环宽度为5 mWb。

系统模型建好后，设定初始转速和初始励磁，开始仿真。设定异步电动机空载起动，在进入稳定运行阶段后，再加入10 Nm额定负载，得到改进扇区判断方法和普通方案的性能曲线如图5~图8所示。

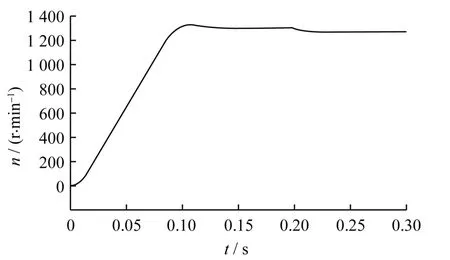
图5 普通方案的转速响应

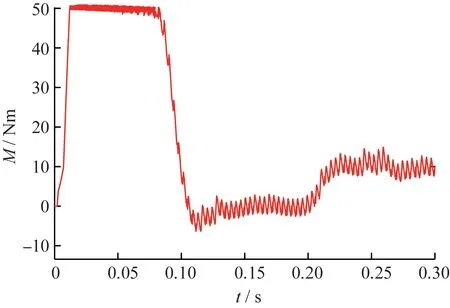
图8 改进方案的转矩响应

对比图5与图6可知，从仿真情况看，改进的扇区位置判断方法和利用定子磁链幅值和角度判断扇区位置的方法在转速响应上没有太大区别，上升时间和最高转速基本相同。但由图7和图8可知，改进的控制方案转矩响应曲线更平滑、波动范围更小，转矩控制精度更高。

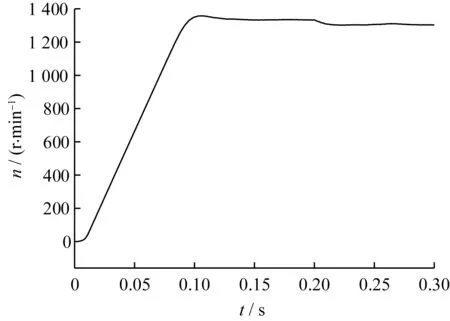
图6 改进方案的转速响应

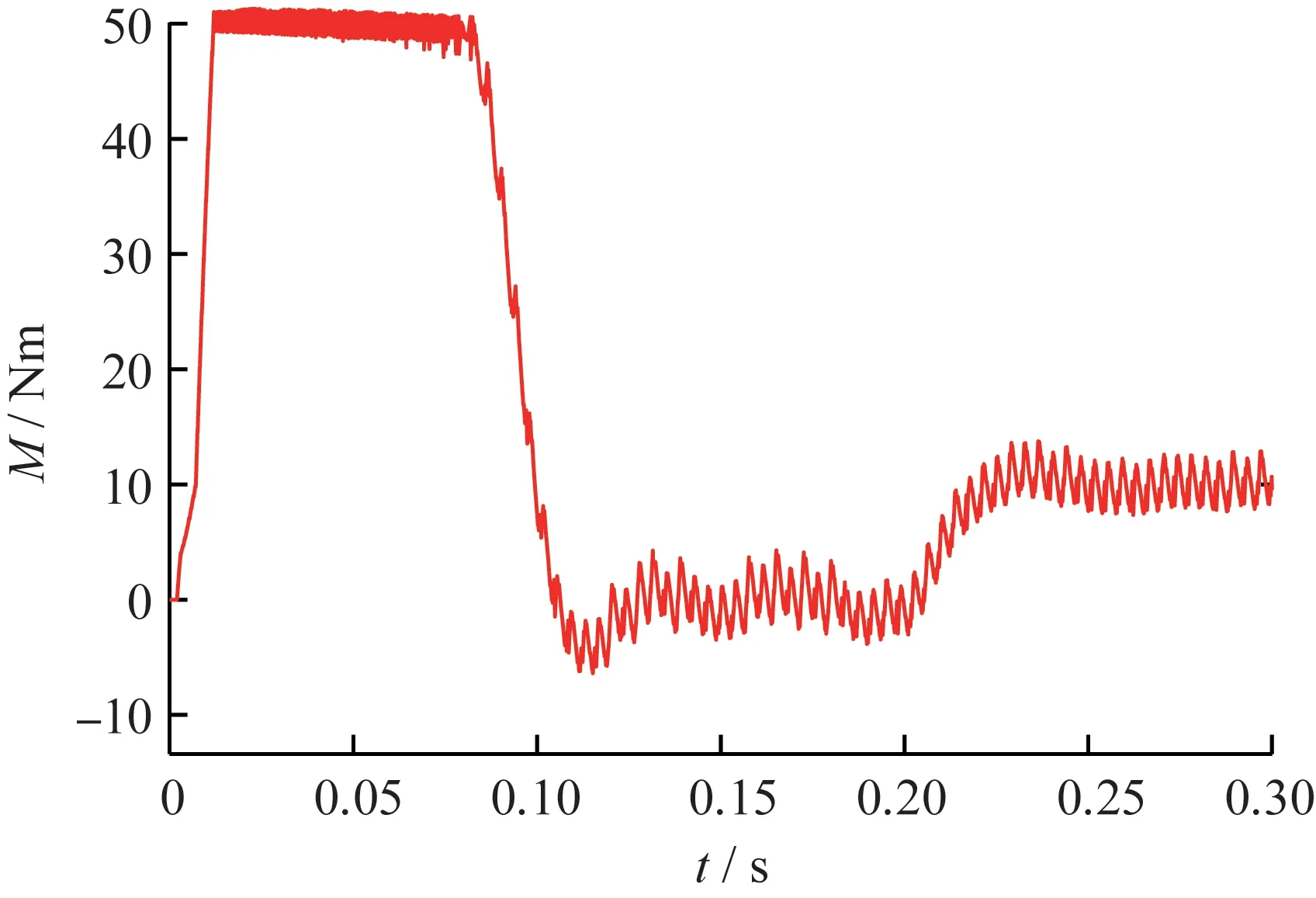
图7 普通方案的转矩响应

为检验系统的抗干扰性和稳定性，给系统负载加入1 Nm的随机扰动，得到普通方法和改进方法的转矩响应曲线对比如图9和图10所示。

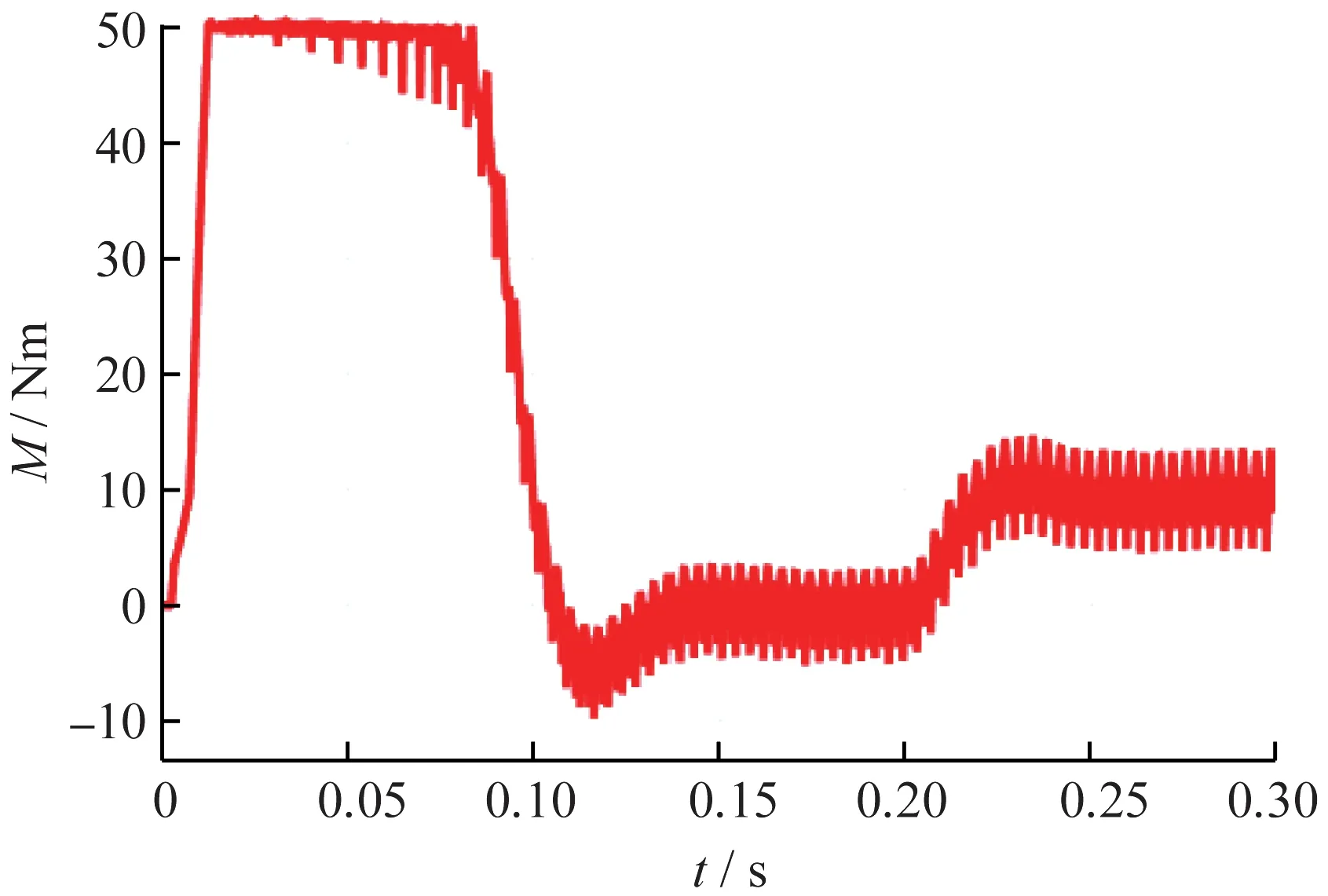
图9 有扰动的普通方案转矩响应

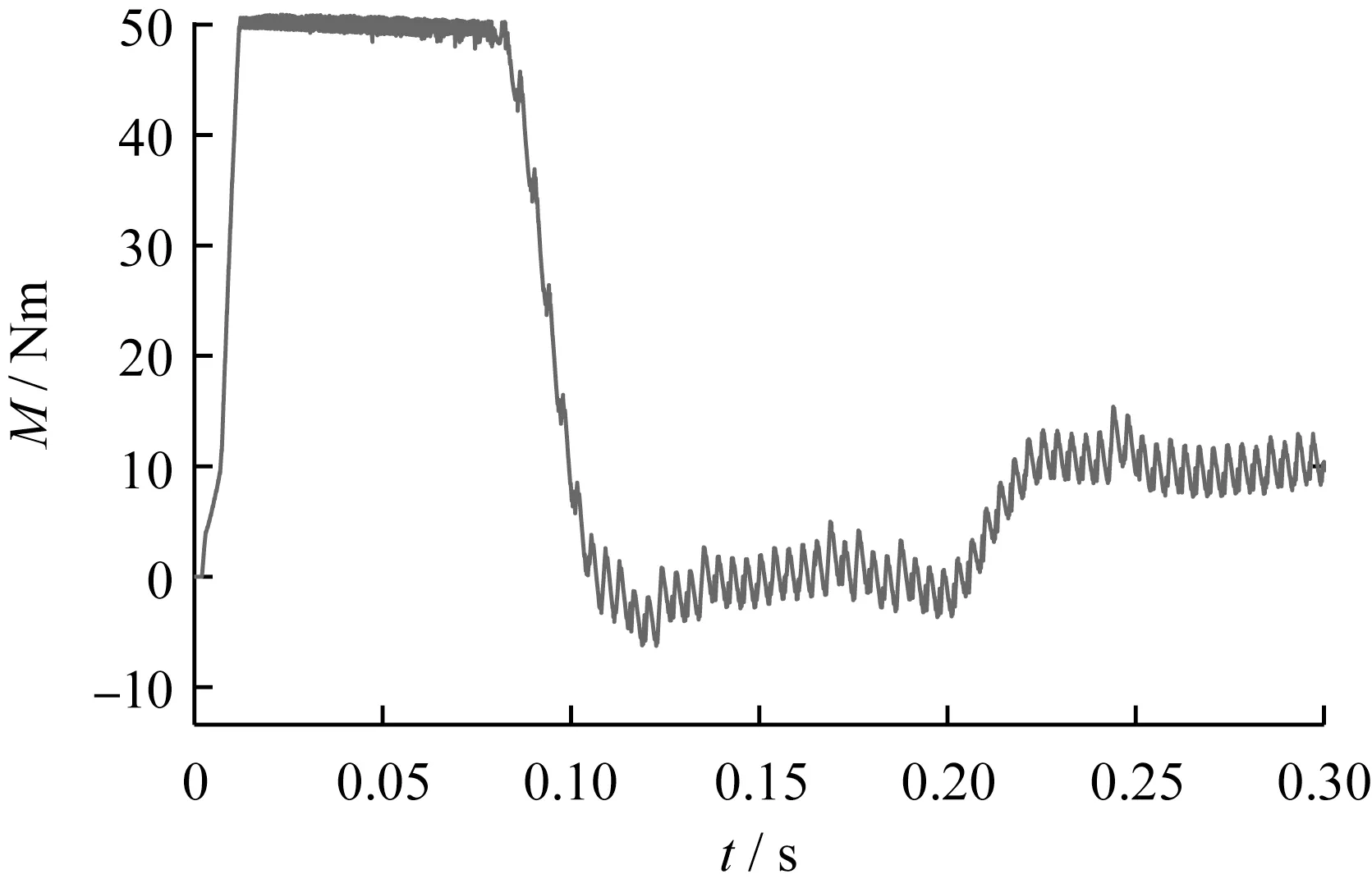
图10 有扰动的改进方案转矩响应

由图9和图10可知，在加入负载扰动后，改进方案相比普通方案依然具备更稳定、平滑的转矩曲线，波动范围更小，体现了改进方案良好的鲁棒形和转矩控制精度。

综上所述，相比普通方案利用定子磁链的幅值和角度进行位置判断的方法，该改进方法在电动机响应速度、转矩响应速度和稳定性上具有一定的优势，且该方法程序算法更简洁，在实际运用中可在一定程度上缩短控制系统处理的时间，有利于提高系统速度，从而降低控制器的性能要求和系统成本。

4 结 论

本文针对异步电动机DTC系统定子磁链位置判断方法较复杂，缺乏论述的问题，提出一种简单可行的判断方法，并结合现有理论设计了一套DTC方案。分别建立了改进磁链位置判断方法和传统利用磁链幅值和角度判断位置的方法的Matlab仿真模型。从仿真结果看，验证了该改进方案的正确性和可行性。该系统具备良好的动、静态性能，鲁棒性以及抗干扰能力，具有和一般方案媲美的控制性能。同时，由于控制算法更简洁，可在原理上缩短控制周期，降低对控制器的性能要求，从而降低系统成本，有利于促进DTC系统的推广运用。