基于模糊控制的永磁接触器动态合闸过程优化

赵路尧，迟长春，籍海亮

（上海电机学院电气学院，上海201306）

接触器作为低压电器中的重要一员，可实现远距离频繁的接通和分断。传统上使用较多的电磁接触器运行时，由于长时间的通电运行，不仅耗电大，还会引起接触器工作线圈温度升高，影响接触器的可靠性和工作寿命；且噪声大，容易受到电网波动的影响，从而导致被控对象短时断电，对企业造成危害。永磁接触器高效、节能性能优于传统的电磁接触器，已被广泛使用［1］。近年来有许多针对永磁接触器的研究。吴昊等[2]采用永磁机构代替电磁机构作为操动机构，改进了接触器结构，提高了永磁接触器的可靠性。文献［3-4］对大功率永磁直流接触器进行了电磁设计和建模研究，优化了永磁接触器动态响应。孙曙光等[5]结合不同振动加速度和频率下接触器关键机构动态特性的差异，获取振动因素变化对交流接触器关键机构动态特性的影响。文献［6-7］提出一种带分断保护装置的智能永磁交流接触器，解决了永磁接触器无法分断的问题。赵升等[8]结合永磁和机械运动动态耦合计算，提高了计算效率，有效减少了永磁接触器耗能。文献［9-12］利用遗传算法和模糊控制算法解决合闸过程中动、静触头接触引起的振动弹跳问题。刘月华等[13]结合C型外磁轭的永磁接触器磁系统结构的优势和静态工作特性，为该类接触器优化设计提供参考。

永磁接触器的运动过程涵盖磁电混合、机械运动以及温度场相互作用，是个极其复杂的过程［14］。因此，研究永磁接触器时，建模和仿真极其重要。通过分析永磁接触器的具体合闸过程，建立相应模型，并借助于Matlab实现对永磁接触器的性能预测，探寻改善永磁接触器的动态合闸特性方法，降低永磁接触器触头运动速度，实现动铁心的软着陆，对永磁接触器的寿命和整体性能提高有着重要意义。

1 永磁接触器模型分析

本文研究对象为圆柱形操作机构的永磁接触器。相比双E型操作机构和双稳态操作机构，圆柱形操作机构永磁接触器占地面积更小，其模型如图1所示。电磁系统、触点系统和消弧系统是永磁接触器的主要组成部分。电磁系统主要包括电磁线圈、永磁体、动铁心、静铁心及相应的电子驱动模块等；触点系统主要由动触头、静触头等构成；消弧系统用来保证触头断开电路时，能够可靠熄灭产生的电弧，支架、弹簧起支撑的作用。动铁心和触头弹簧由塑料支柱连接，而动触头与触头之间有触柱，用于支撑，上述部件均可移动。永磁体和静铁心对电磁线圈起固定作用，反力弹簧将可运动部分和电磁线圈进行连接，使之构成一个整体。

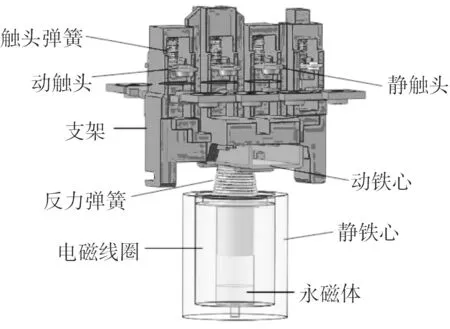
图1 永磁接触器模型

1.1 控制电路模型

永磁接触器控制主电路由电磁线圈、二极管与电容构成，如图2所示。电磁线圈部分分别由线圈电阻和电感器件组成。当永磁接触器闭合时，开关S1、S3闭合，开关S2关断，交流电流经过D1整流和电容C1滤波后通入电磁线圈，实现永磁接触器的闭合过程。在永磁接触器闭合过程结束后，开关S3关断，电容C2通入电流，C2开始储能，稍后，关断S1。当永磁接触器需要结束关闭过程，开始分闸时，通过闭合开关S2，使得电容C2中储存的电能开始释能，对电磁线圈反向通电，进而减弱永磁体对动铁心的电磁力，在反向电流以及反力弹簧和触头弹簧共同作用下，完成其分闸过程。控制电路模型如图2所示。

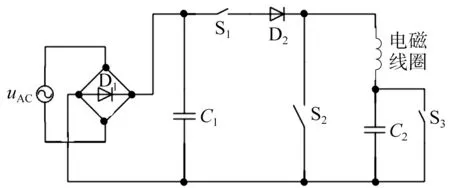
图2 控制电路模型

永磁接触器合闸过程所满足的电压平衡方程为

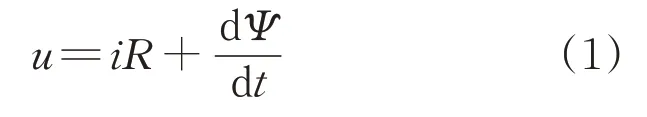
式中：u为电磁线圈上的电压；i为电磁线圈电流；R为电磁线圈电阻；Ψ为电磁线圈磁链。

1.2 机械运动模型

为了简化永磁接触器复杂的合闸过程，本文忽略触头、弹簧的作用和可运动部分质量的变化，将合闸过程分为两部分分析。

（1）永磁接触器动铁心达到超程的位置。此时，反力弹簧对永磁接触器施加反力作用，其反力弹簧所承受的反作用力为

式中：x为可移动部分位移；k1为反力弹簧的弹性系数，此处取0.305 N/mm；a为弹簧初始压力，取值为2.194 N。

该阶段满足达朗贝尔机械运动方程，有

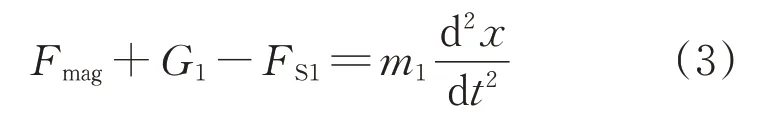
式中：Fmag为动铁心所受电磁力；G1为动铁心重力；m1为动铁心质量，取值为53.4 g。

（2）永磁接触器由超程位置到闭合位置。此时，反力弹簧和其触头弹簧共同对永磁接触器施加反力作用，其共同作用力为

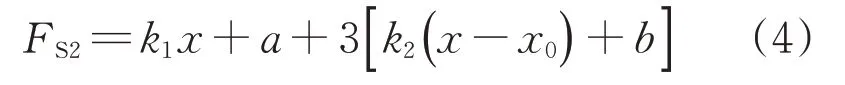
式中：k2为触头弹簧弹性系数，取值为0.36 N/mm；x0为超程位置，取值为4.30 mm；b为反力弹簧初始预压力，取值为1.663 2 N。

该阶段满足达朗贝尔机械运动方程，有

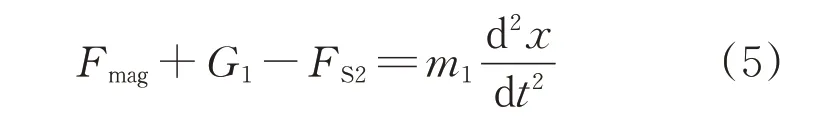
根据上述公式，基于Matlab可以建立永磁接触器合闸过程的机械运动仿真模型，如图3所示。模型中采用切换开关来控制弹簧作用力的切换。

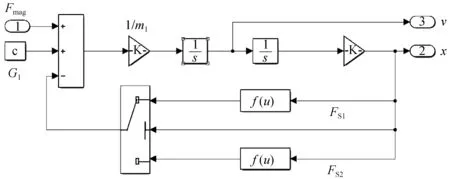
图3 机械运动仿真模型

图3中，K为增益模块，增益量为1m1；1/s模块主要功能是将输入量对时间进行积分，输入加速度的值经1/s模块对时间积分得到速度值，若输入的是速度值，经过1/s模块对时间积分得到的是位移值；f(u)为调用函数模块，分别对应式（2）和式（4）。

1.3 模糊控制器建立

模糊控制器常见的推理模型有Mamdani模型和Sugeno模型。两者最大区别在于其模糊控制规则制定部分，IF部分相似，但THEN部分相差很大。Sugeno模型通常是精确函数，Mamdani模型则是模糊量。本文采用Mamdani模型，对该模型进行分析的模糊控制器结构是较为常见、应用更加广泛的模糊控制。图4为Mamdani模型的模糊控制结构关系。

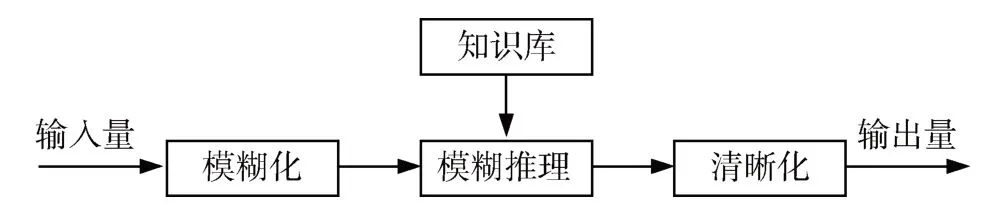
图4 Mamdani模型的模糊控制结构关系

由图4可知，模糊控制系统主要由4部分组成，分别是模糊化、模糊推理、知识库、清晰化［15］。其中模糊化是模糊控制的一个重要环节，将输入量的确定值进行离散化，转化为相应模糊变量值。知识库由数据库和规则库组成，数据库提供处理模糊数据的相关定义，其涵盖内容有各语言变量的隶属度函数、尺度变化因子以及模糊控制的分级数等；规则库中则包含模糊控制规则，数据库和规则库两个部分反映了控制专家的经验知识。模糊推理则是将输入的模糊变量基于知识库分析处理后，得到模糊输出变量。清晰化则是将模糊输出变量通过比例因子转为清晰量，得出最终的输出控制变量。这4个部分都完成后，整个模糊控制系统完成相应的工作。由于永磁接触器的运动过程涵盖磁电混合、机械运动以及温度场相互作用，是个极其复杂的过程，又鉴于模糊控制对控制对象不需要精确模型，可操作性和实现性较强，并且对过程参量变化不敏感，实现方法比较简单。因此，通过加入模糊控制的方法来调节永磁接触器合闸时动铁心和动触头速率，使触头碰撞出能量，以便优化永磁接触器性能。本文以PWM占空比D作为模糊控制器的输出量，输入量为动铁心位移距离x和速率变量v。例如，若x为S，v为S，则D为L。在x和v较小时，通过增加D来提高v，从而缩短关闭时间。本文基于Mamdani模糊推理算法，即系统的模糊输出是通过对有效的模糊输出作最大化运算来应用模糊控制推理过程，去模糊化处理基于最大最小合成，去模糊值在5%~25%，每一种模糊语言的变量取值[0，1]。模糊控制规则如表1所示，隶属函数如图5所示，其中S、M、L分别表示小、中、大。

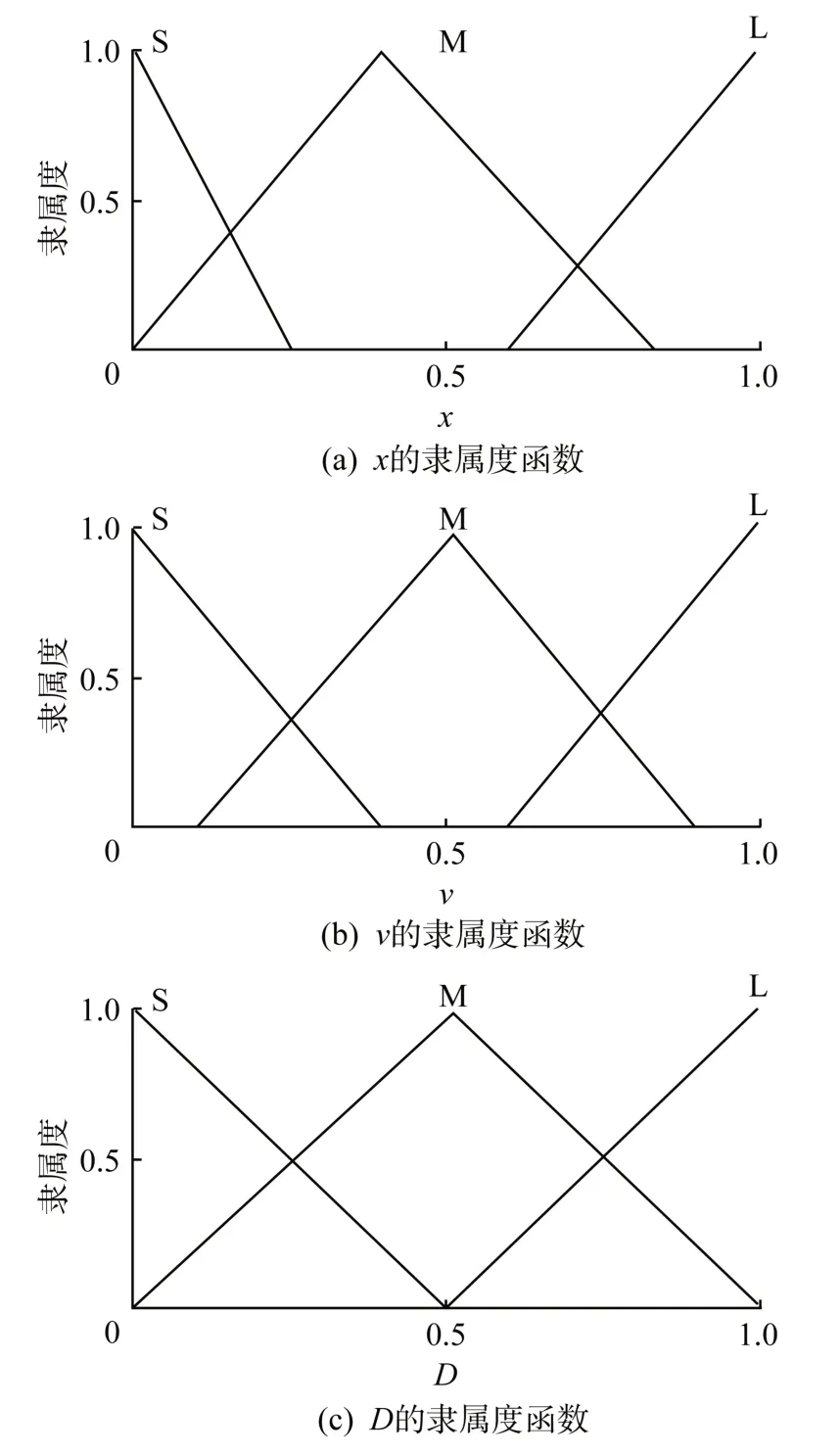
图5 模糊输入x、v与输出D的隶属函数

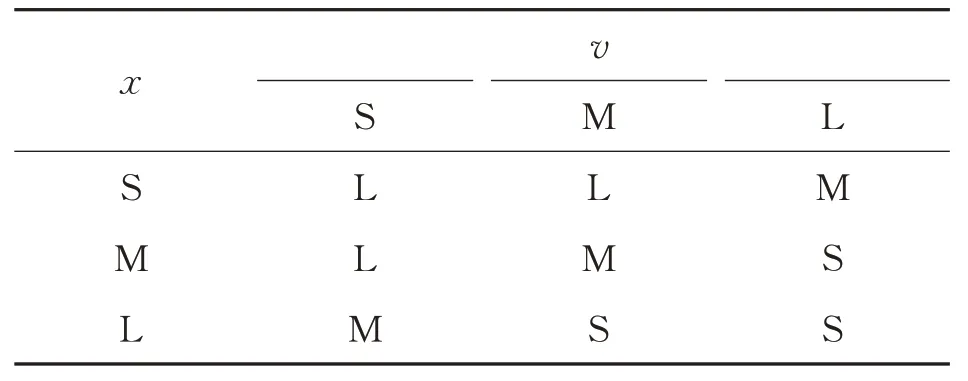
表1 模糊控制规则表

2 模糊控制系统仿真

仿真的模糊控制系统如图6所示。本文将模糊元函数[0，1]均分为5份，控制D的取值，可以通过取区间中间值确立，例如区间[0，0.4]，选择0.2作为其占空比。PWM周期可由实际情况选择设置为2 ms来得到较为直观的波形。仿真初始条件为常量不变，设置动铁心初始速度为0，动铁心初始位移为0，仿真结束时若动铁心最大位移为7.06 mm，则仿真完成。

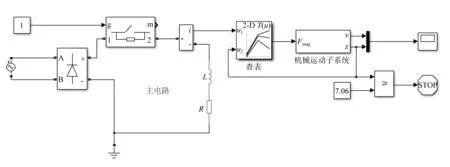
图6 模糊控制系统

仿真结果如图7所示。由图可知，加入模糊控制后，动铁心末速度明显减小，动静触头碰撞能量关系式为

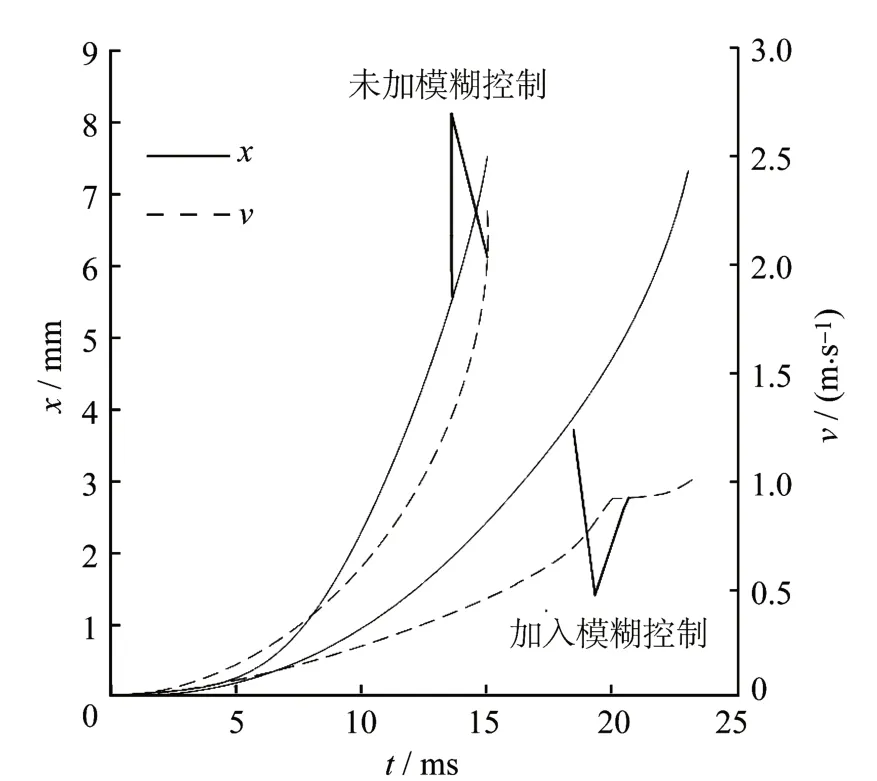
图7 仿真结果

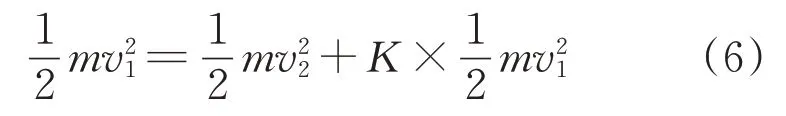
式中：m为动触头的质量；K为触头材料恢复系数；v1为动触头末速度；v2为动铁心末速度。

由式（6）可知，减少触头弹跳的碰撞能量，可以适当减少触头质量和运动速度。碰撞能量减少后，触头的弹跳次数必然减少。

考虑到220 V交流电压经过整理后，其合闸开通相位角约束范围为0°~180°。因此，选择以合闸开通相位角为变量，每次实验开通相位角的幅值变化均为30°，进行仿真分析，详见表2。

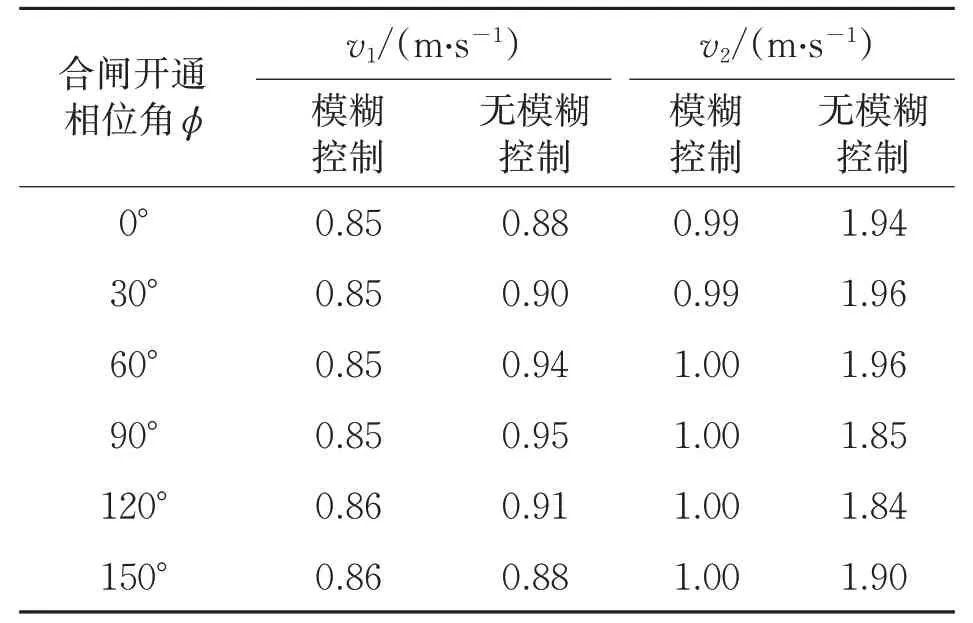
表2 不同合闸开通相位角下有无模糊控制方法对比

由表2可知，选取不同的合闸开通相位角，加入模糊控制后，v1最大相差为0.1 m/s，v2最大相差为0.97 m/s。由此可见模糊控制方法对减小v1和v2有较大作用。由式（6）可知，v1和v2减小时，可有效地减小碰撞能量，从而使触头弹跳次数减少，这对优化其动态性能有较大意义。

3 结 语

本文为了提高永磁接触器使用寿命，针对使用可靠性的需求，分析了永磁接触器的物理模型以及合闸过程的机械运动模型，归纳出基于Mamdani模型优化模糊控制的方法，实现了永磁接触器动态合闸特性的优化。在实验方面，基于Matlab通过查表模块连接主电路和机械运动模型，建立永磁接触器合闸仿真系统，并针对永磁接触器合闸开通不同相位角对触头速度的影响进行了仿真实验。实验结果验证了基于Mamdani模型的模糊控制对优化永磁接触器动态性能的可行性和高效性。