基于改进型变步长与模糊控制的MPPT控制策略

程 超

（安徽淮南平圩发电有限责任公司发电部，淮南232038）

近几年，科研人员对太阳能光伏发电系统最大功率点跟踪（Maximum Power Point Tracking，MPPT）开展了创新和研究，提出了较多的控制策略［1-2］。根据现实的机制与控制算法特点特征，可分为3类：基于优化数学模型的间接控制策略、基于采样数据的直接控制策略与基于先进控制理论的MPPT算法策略。

（1）基于优化数学模型的间接控制策略。包含：短路电流系数法、恒定电压法、开路电压系数法［3-4］。恒定电压法，主要是在温度恒定时，太阳能光伏电池会随着光照强度的变化对外输出单峰值特性的功率曲线，而这时太阳能电池将工作在最大功率点上。但太阳能光伏电池对外部温度的要求比较苛刻，一旦外部的温度发生突变，将会对系统带来较大的误差。短路电流系数法和开路电压系数法原理相同，均是在恒定电压法上进行优化，主要是应对温度变化带来的偏差；但不足之处在于需要周期性地开断负载和太阳能光伏电池，检测开路端电压，这会造成一定的功率损耗，得出的并不一定是最大功率。

（2）基于采样数据的直接控制策略。包含：扰动观察法、电导增量法等，这一类控制策略需要连续采集相关太阳能电池的端电流和端电压，利用采样的数据直接控制对应系统工作点，其鲁棒性能较好，精度较高［5-6］。两者共同之处是对太阳能电池的输出电压不间断地施加扰动追踪最大功率点，差别在于电导增量法一旦到达了最大功率点就不需要给予扰动。

（3）基于先进控制理论的MPPT算法策略。这一类控制算法特点是以最新控制理论基础为前提，对于太阳能光伏发电系统功率输出的时不变性与强非线性特点，提出了新的控制算法，比如模糊控制算法、滑模控制、神经算法等［7-9］。神经算法运用在MPPT上有较高的精度，但需要大量地训练光伏电池板的输入输出参数，才能获得相应的控制规则，若电池板不同，参数变化，训练操作就会繁琐。滑模控制结构的变量为S，若S<0，则滑模输出变量Uh=1；若S>0，则Uh=0。利用开关变化的特点，强迫系统在允许范围内的轨道周边做高频率、小幅度的滑模上下运动，以此保持并运行在预设的滑动曲面上。

光伏发电系统的输出特性易受外界影响而出现非对称的强非线性特征，输出的功率会偏离最大输出功率点。针对这一问题，本文分析了MPPT的几种常用控制策略的优缺点，在上述分析基础上作进一步改进，通过变步长算法先对光伏电池的输出功率进行迅速跟踪，并采用模糊控制策略对其进行二次优化锁定跟踪，以此减少响应时间与振荡，提升光伏发电系统的稳定性。

1 光伏电池输出特性

光伏电池是通过其半导体材质实现光能的物化反应，将太阳的光能转化为电力能［10-11］。太阳能光伏发电等效电路如图1所示。其中，Ipv为光伏电池输出电流；Iph为光生电流；Rsh为等效并联电阻；Rs为等效串联电阻；I0为二极管半导体的反向饱和电流；RL为外接负载电阻；Ish为等效并联电流；UD为暗电压，即光伏电池在无光环境下由外电压作用内部PN结所流通的单向电压；C为电容；Upv为光伏电池的输出电压。随着工作温度、太阳光照强度等外界环境的变化，太阳能发电存在间歇性、非线性的现象。

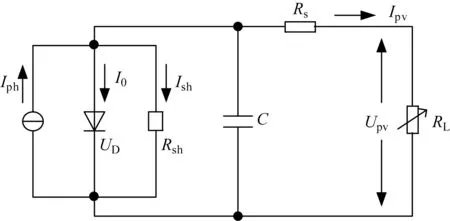
图1 太阳能光伏发电的等效电路

图1对应数学模型方程为

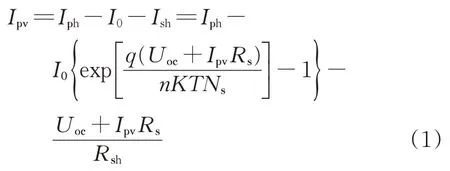
式中：Uoc为电阳能光伏电池的开路电压；Ns为串联电池数；K为玻尔兹曼常数，一般取1.38×10-23J；T为绝对温度；n为光伏电池的数量；q为单位电荷数。

实际太阳能光伏电池工作时，随着太阳光照强度的变化，会对输出电流影响较大，不能得到精确数据。因此，在实际工作中常采用工程型的太阳能光伏电池模型，即

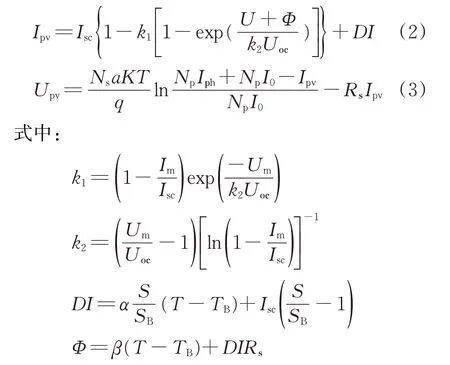
Isc为短路电流；k1为偏差电流的校正系数；k2为偏差电压的校正系数；U为光伏电池输出电压；Φ为校正后的电压偏差值；D为导通占空比；I为输出电流；Np为太阳能电池组件并联数；a为校正系数；SB为标准光照辐射强度；TB为环境温度；α为电流的温度系数，A/℃；β为电压温度系数，V/℃；S为现实工作光照辐射的强度；Um为光伏电池在最大功率点的电压；Im为光伏电池在最大功率点的电流。

太阳能光伏电池的输出功率为

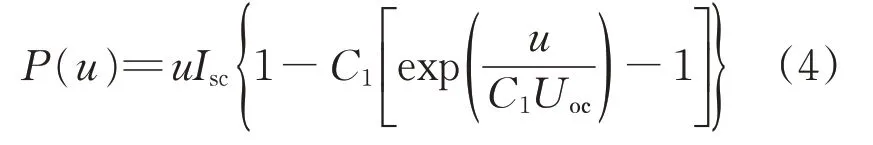
式中：u为光伏电池实际输出电压；C1为并联电容。

由式（2）~（4）模拟经验函数曲线，选取光伏电池相关的仿真参数。具体建模参数分别如表1和表2所示。其中，Pmax为最大功率。

表1 光伏阵列工程参数

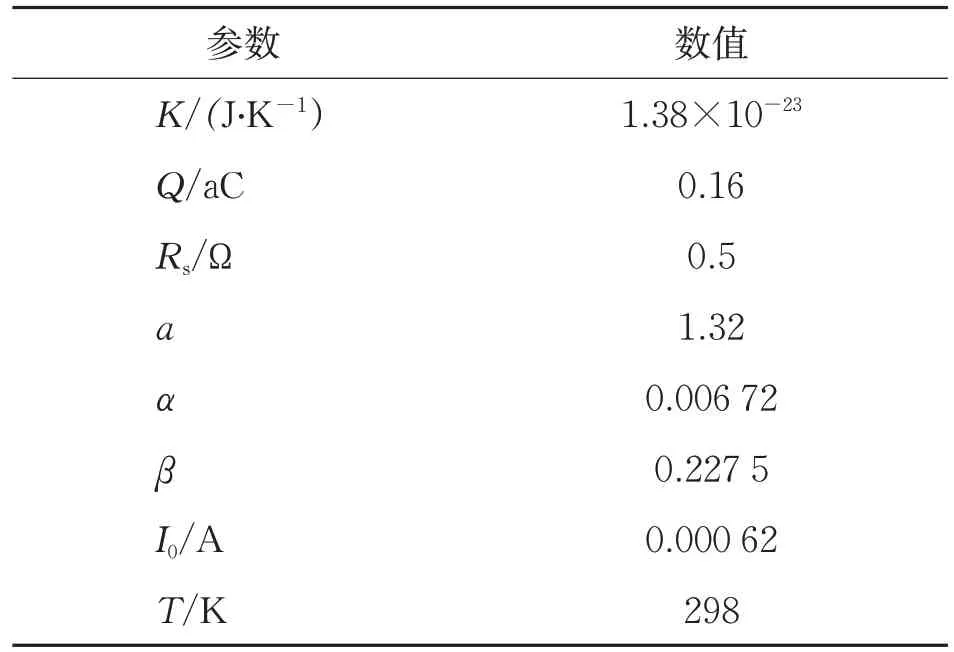
表2 光伏阵列仿真的拟合参数

2 变步长部分

传统定步长响应速度及跟踪精度都有一定程度缺点，科研人员大多采用变步长的控制策略［12-13］，一般分为两种：

（1）依据相关光伏输出功率的一次导数值大小，赋予快慢不同的步长值。

（2）将光伏输出功率的一次导数P'（u）作为扰动变步长的参数，由此步长将在最大功率点两侧做自适应性的相关调整。比如，若工作于最大功率点左侧，则进行正向扰动；若在最大功率点右侧，则反向扰动；当接近最大功率点时，步长会自动变小。

对光伏输出功率P（u）进行一阶求导，可得P'（u）数学表达式为

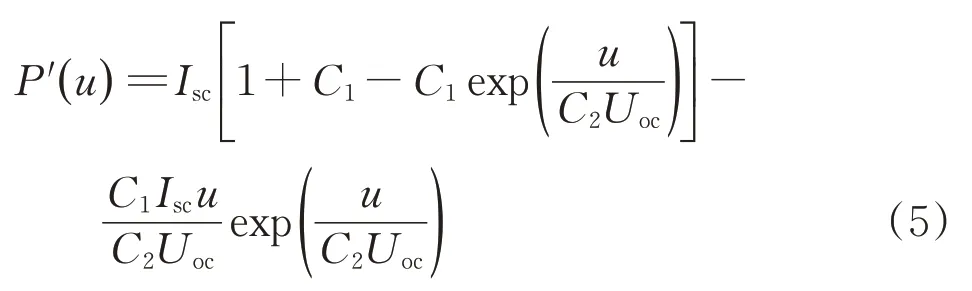
式中：C2为串联电容。

标准测试状况下，P'（u）若工作在最大功率点左侧，P'（u）为正；若工作在最大功率点右侧，P'（u）为负。这与扰动方向的要求基本吻合，且左右侧是∣u-Um∣单调减函数，符合步长变化的参数要求。

第k个周期的占空比为

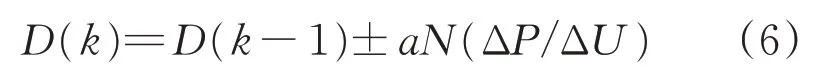
式中：N为调整变步长的系数，一般的变步长算法中，N就是P'（u）；ΔP为输出功率的变化量；ΔU为输出电压的变化量。

本文优化的变步长部分，取N=arctan［P'（u）］，a按照实际较大的输出特性取值。

变步长参数的变化率如图2所示。变步长系数N的一阶导数，依照高等函数中的反三角求导公式计算如下：

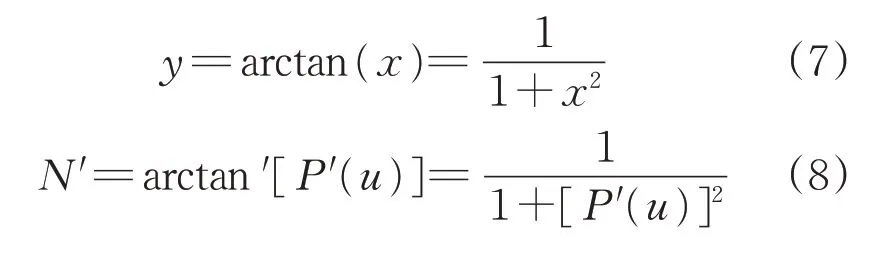
图2 变步长参数的变化率

本文为了取得更好的效果，将变步长和非对称的模糊控制相结合。当光伏输出工作在远离最大功率点时，优化的变步长会使其迅速靠近最大功率点，但当逐步接近最大功率点预设的核心范围区间时，通过非对称的模糊逻辑控制对其进行寻优。

3 模糊部分

太阳能光伏发电的输出特性曲线不易用精准的数学模型表示，因其具有较强的非线性特征。太阳能光伏电池的MPPT也不需要特别的光伏电池模型，只需要不断地调整可控参数值，使其输出特性曲线逐渐靠近最大功率点。该过程符合对于被控目标对象的模糊控制特征。因此，对于太阳能光伏电池的MPPT采用模糊控制相对合适［13-14］。图3所示为非对称模糊控制策略框图。

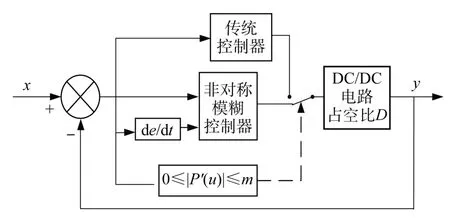
图3 非对称模糊控制策略框图

模糊PI参数的自整定结构框图，如图4所示。

图4基本原理是：先将实时检测的系统并网电流的每个周期里的数值igrid，与规定的电网电流值iref作比较，得出误差信号e，然后将误差信号e依次输入到模糊控制器与PI控制器中。模糊控制器依据相应的模糊规则输入误差的变化率与输入误差，将输出变量ΔKp与ΔKi输入到PI控制器中，分别与预先设定好的比例系数Kpo、积分系数Kio进行计算，从而达到实时调整的效果。

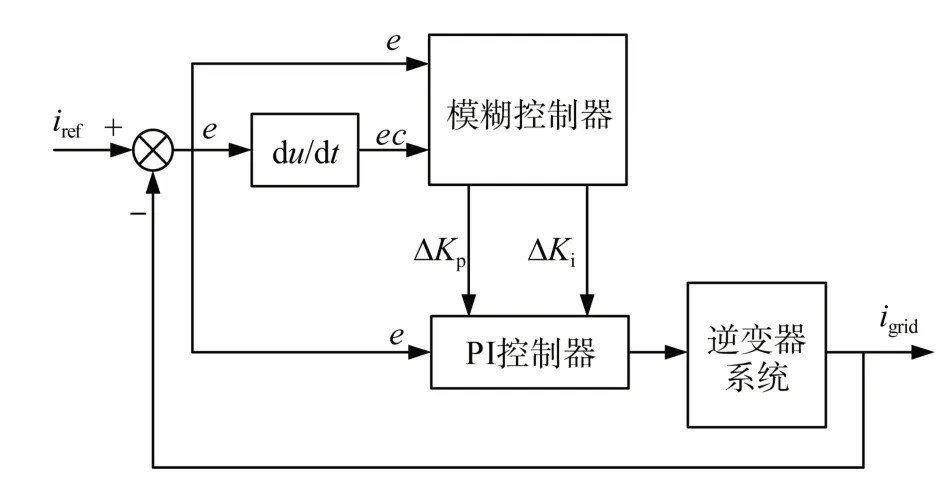
图4 模糊PI参数的自整定结构框图

模糊PI参数自整定的计算式为

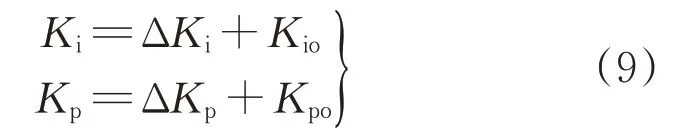
通过模糊PI参数自整定，找出PI的两个参数Kp、Ki与误差e、误差变化ec之间的模糊关系。运行中不断检测e和ec，根据控制原理对两个参数在线修改，以满足e和ec不同时对控制参数的要求，从而使系统具有良好的动、静态性能。在线运行时，控制系统通过对模糊逻辑规则的结果处理、查表和运算，从而完成对PI参数的在线调整。具体的工作流程如图5所示。其中，r（k）为第1个输入因变量；y（k）第2个输入因变量。

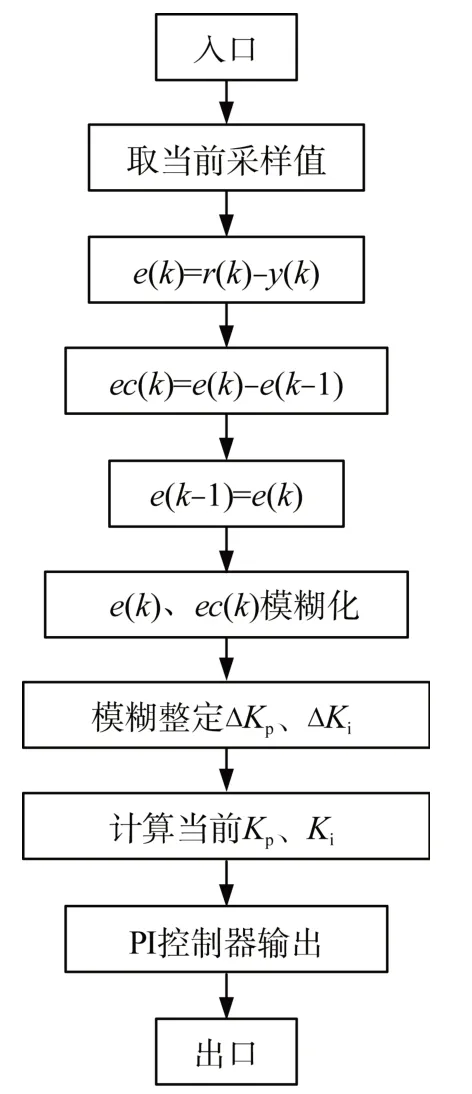
图5 模糊PI工作流程图

本文利用Matlab/Simulink工具箱实现模糊PI控制。该工具箱具有简单易懂，方便调节参数的特点。按照模糊PI整定规则设置模糊工具箱，隶属度函数选为三角函数，误差e和误差的变化率ec的论域分别为［-150，150］、［-3.5，0.5］，输出的模糊规则图形如图6、图7所示。

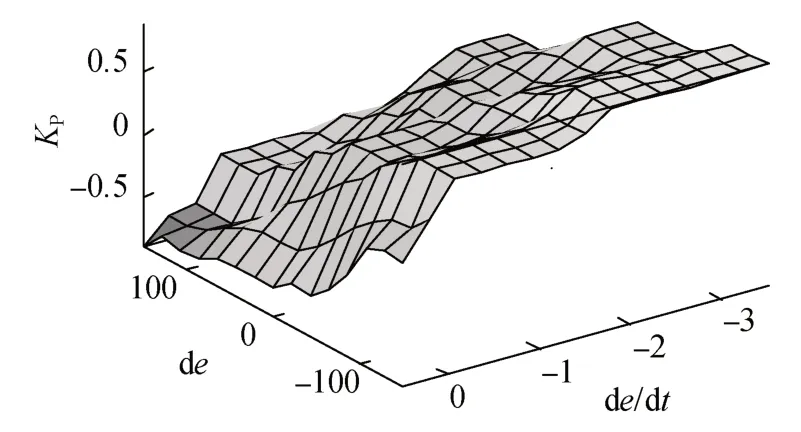
图6 输出量ΔK p的模糊规则图形

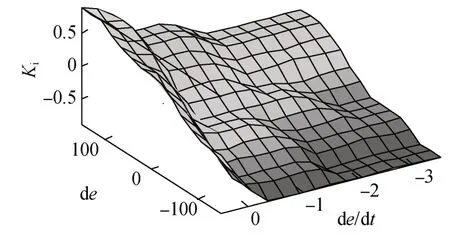
图7 输出量ΔK i的模糊规则图形

4 仿真与分析

在Matlab/Simulink中建立仿真模型，仿真模型由光伏电池、Boost电路及电阻性负载组成[15]。部分参数为：太阳能光伏电池最大电流Isc=3.5 A，最大功率点的电流Im=3 A，最大输出电压Uoc=600 V，最大功率点的电压Um=380 V，电阻R=100Ω。模糊PI控制器初始参数Kp=4.5，Ki=20.5。光伏发电系统中两个电容值从左到右依次为10μF、1μF，电感L值设为0.2 H，采用ode45算法仿真。设定光伏电池面板温度T=25℃，光照强度S由1 kW/m2骤升至1.2 kW/m2再骤降至800 W/m2，分别对定步长、变步长[11]和改进的变步长的MPPT技术进行仿真。仿真结果如图8所示，光伏阵列各工作阶段功率变化如表4所示。

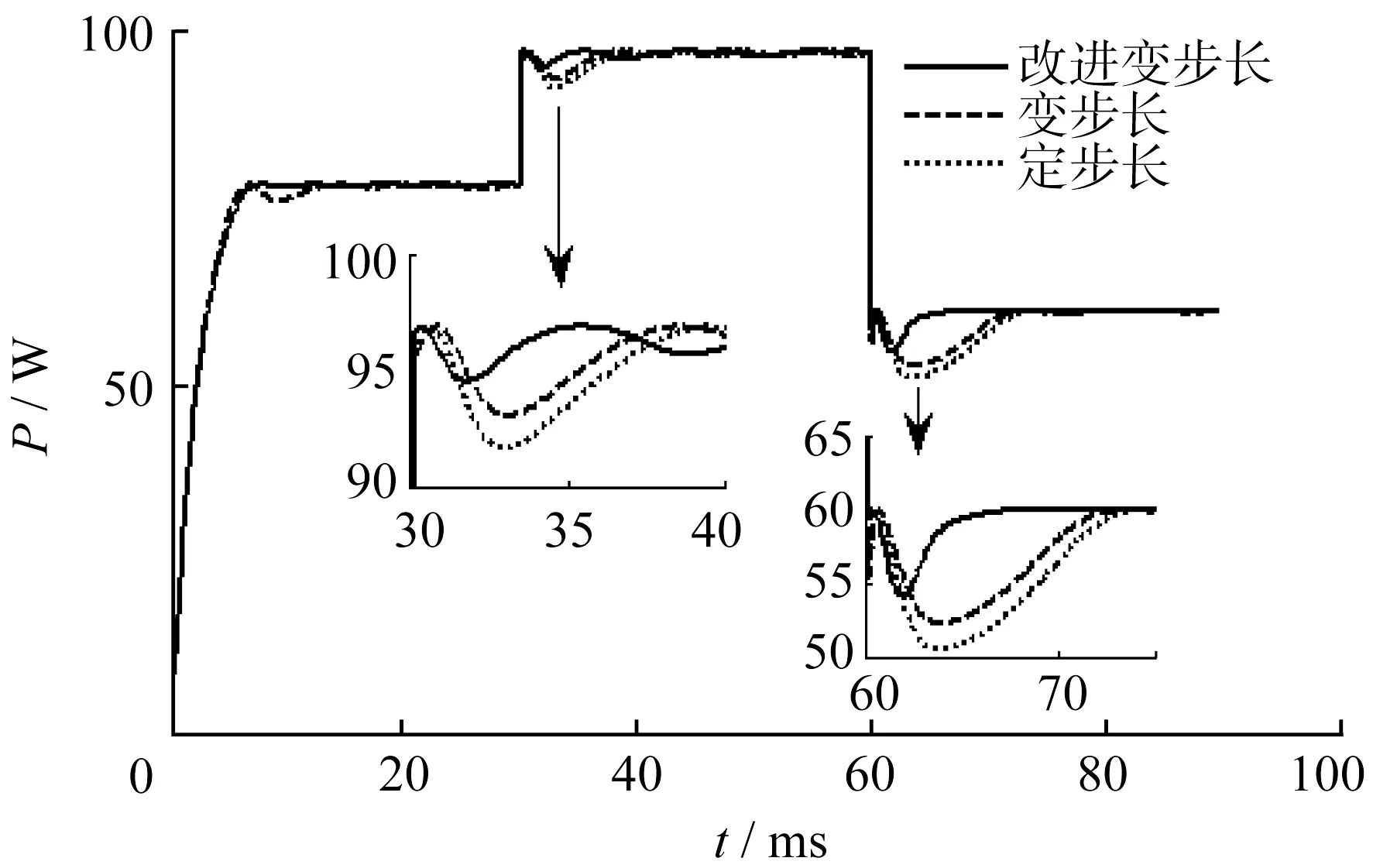
图8 仿真结果对比图

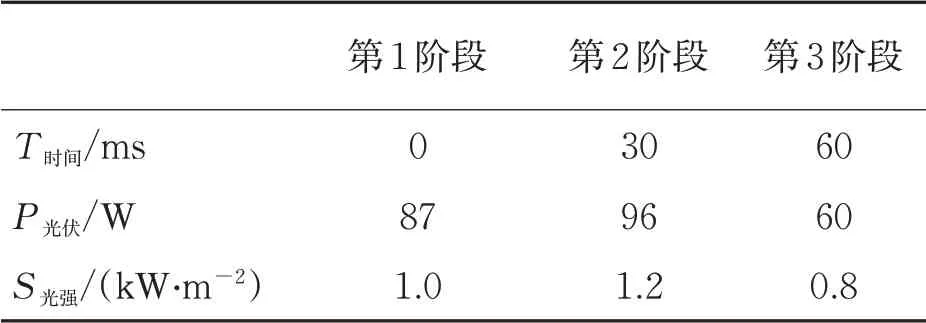
表4 光伏阵列各工作阶段功率变化

由图8与表4可知，第1阶段，在0~30 ms时段，光伏系统功率约为87 W，光照强度为1 kW/m2；第2阶段，由于在第30 ms时刻，调节扰动使得光照强度上升到1.2 kW/m2，光伏发电功率在30 ms时刻迅速增加至96 W；接着，第3阶段，在60 ms时刻，通过调节扰动使得光照强度下降到800 W/m2，负荷功率在60 ms时刻下降到60 W。

通过图8对比两张局部细节图，能够明显看出采用结合后的优化变步长和非对称模糊控制MPPT算法可以较好地追踪到最大功率点；当太阳能光伏板开始工作时，两种控制策略都可跟踪到最大功率点。然而，优化后的变步长和非对称模糊MPPT控制算法运行更平稳，无较大的振荡，当外部光照强度环境参数发生改变时，太阳能光伏发电系统也可以迅速而精确地追踪到最大功率点，表现出良好的稳定性。整个过程中，采用结合后的优化变步长和非对称的模糊控制算法比传统的定步长MPPT控制策略优异些。

5 结 论

基于传统变步长在光伏发电的最大功率点附近出现的振荡，以及前期跟踪精度不足的现状，针对性地提出采用非对称模糊结合优化变步长参数的新型控制策略方法，并在Matlab上进行验证仿真。研究表明，该新型控制策略方法具有动态可靠性与优异性。在其他方面，对大功率、多种电源形式的并网发电系统，有待进一步研究。