立式上行管内液固两相流中椭球形颗粒分布和运动特性

彭德其， 王依然， 侯家鑫， 俞天兰， 吴淑英， 王志平

(1. 湘潭大学机械工程学院， 湖南湘潭411105； 2. 湖南工业大学机械工程学院, 湖南株洲412007；3. 湘潭锅炉有限责任公司, 湖南湘潭411202)

液固两相流换热器具有强化传热及防垢除垢特性，被广泛应用于化工、 海水淡化等工业领域。由于目前实验获取颗粒运动特性的方法对实验设备要求较高， 实验成本受到限制,因此，越来越多学者选择建立各种数值模型解决该问题，其中CFD-DEM模型所需要的经验参数较少，对颗粒尺度微观信息获取较简便，有利于研究液固两相流动的微观机理。

由于球形颗粒简单，过去以球形颗粒为研究对象，使用CFD方法进行研究[1]，如Kerst等[2]通过对液固流化床中两相流实验与CFD-DEM耦合模拟对比， 获得了固体颗粒在流化床中分布形态和运动信息；Wang等[3]的研究表明，竖直液固流化床中流体进口速度增加会增大颗粒在轴向方向的速度；Razzak等[4]发现液固两相中直径较大颗粒有更好的均匀性。在实际应用中颗粒形状多为非球形[5]，由于非球形颗粒建模难度较大，对异形颗粒研究较少。针对这种情况，提出多种模型用于描述非球形颗粒，包括超椭球模型[6-7]、 复合球模型[8]、 多面体模型[9]、 真实形状模型[10]等。借助于这些颗粒模型，近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大进展[11-12]。Ma等[13]建立非结构化CFD网格和棒状颗粒与复杂几何接触检测的CFD-DEM模型,对复杂几何形状的气-固流化床中棒状颗粒流态化进行模拟，发现具有较高的效率和精度。Campbell等[14]研究表明：与普通球形颗粒相比，椭球形颗粒的长径比对剪切流的相变变化有重要影响，椭球形颗粒间更容易形成影响颗粒周边流场变化的“力链”。

上述文献研究对象大部分是微米级粒径球形颗粒及其在流化床流场中运动和分布特性，对大粒径颗粒研究涉及不多。大粒径颗粒相较于微米级颗粒，体积变大， 颗粒运动受阻，颗粒之间容易聚团，而聚团形成与破裂对液固两相运动有较大影响。部分学者针对较大空间池式容器内异形颗粒形状对周围流场影响进行了仿真模拟[15-16]。虽然颗粒形状是引起流化床内流动特性显著变化的重要参数，但对立式换热管内大粒径异形颗粒研究较少。

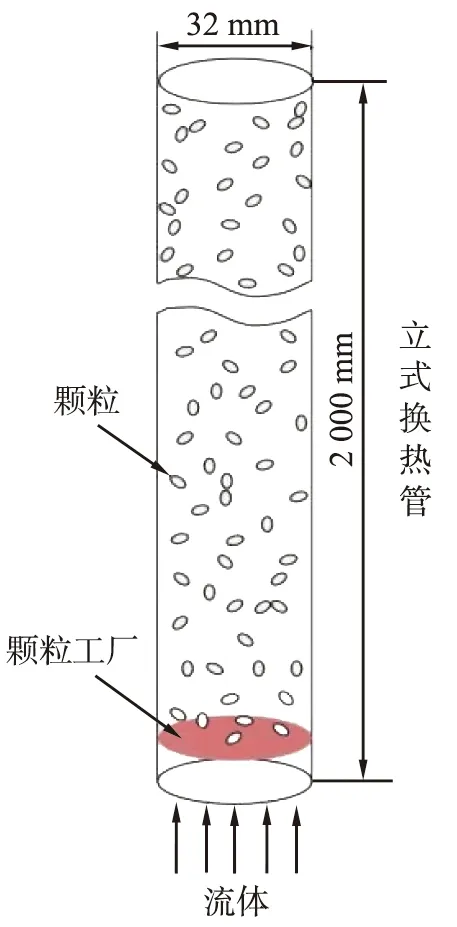
图1 模拟流程图Fig.1 Simulation flow chart

本文中以液固两相流换热设备中立式上行换热管为研究对象，采用CFD-DEM数值模拟方法，对从圆形到长圆形粒子形状的椭球形颗粒的长径比β和颗粒体积分数α进行数值模拟，并深入分析管内椭球形颗粒的分布和运动行为，对进一步阐述立式列管式换热器中液固两相流流动机理和椭球形颗粒在工业换热器中实际应用具有重要意义。

1 研究方法

1.1 模型描述及方案设定

选用常见立式换热管的结构如图1所示。以管底部圆心(0,0,0)位置为参考点，换热管内径Din=32 mm， 换热管高度L=2 000 mm。 不考虑壁厚影响，流体从竖管底部流入，从顶部流出，颗粒工厂位于管底部，流体域体积为1.608 5×10-3m3。椭球形颗粒长径比如图2所示。椭球形颗粒是一个类球体，其中半长径为a，其他2个半短径b、c相等，即b=c，椭球形长径比为半长轴与半短轴之比，即β=a/b。选取体积与半径1 mm的圆球形颗粒相等的不同长径比β的椭球形颗粒进行研究。

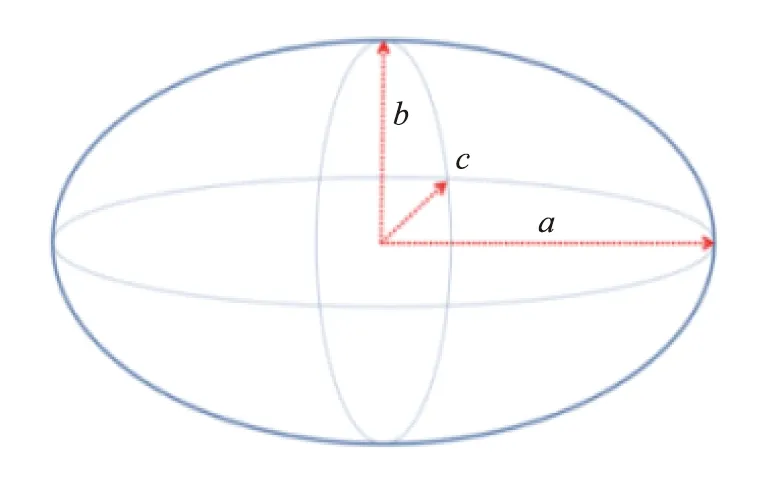
图2 椭球形颗粒长径比示意图Fig.2 Schematic diagram of aspect ratio of ellipsoidal particles

图3为ICEM软件生成的立式直管网格示意图。为兼顾计算精度与工作效率，对管壁面进行边界层加密处理，设置近壁面第1层网格尺寸0.05 mm，增长率1.1，从外往里划分15层，对流体区域使用六面体网格进行划分。同时，DEM和CFD中立式上行管模型网格文件相同。

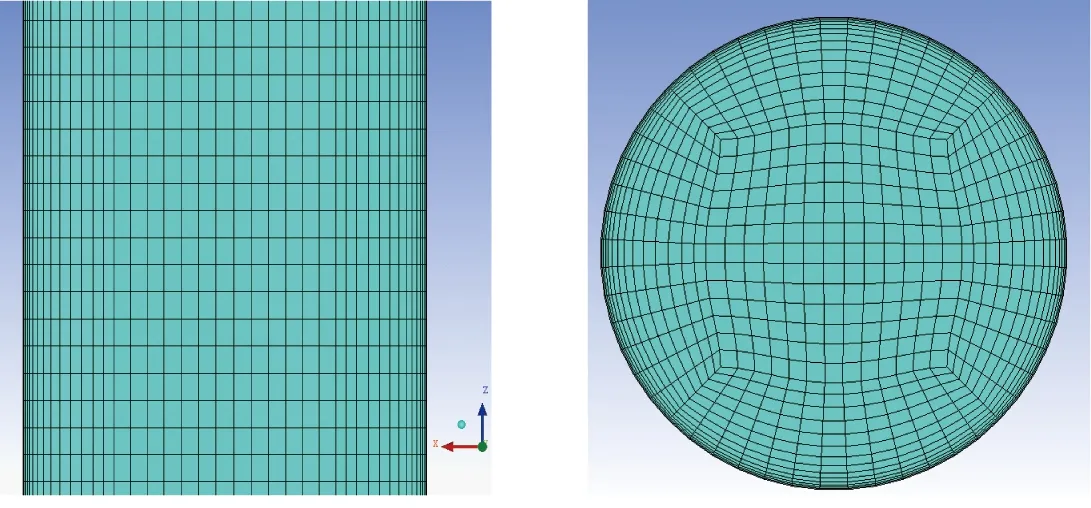
图3 立式上行管网格Fig.3 Vertical upline pipe grid

管内使用水作为流体相，流体物性参数如表1所示。流体进口流速选择实际中广泛应用1.5 m/s。通过改变椭球形颗粒长径比β和颗粒体积分数α，构建了25组不同工况，如表2所示。选取5种不同长径比β椭球形颗粒，采用CFD-DEM的欧拉-拉格朗日耦合方法，颗粒体积分数α要低于10%，考虑到过大颗粒入口浓度会产生较大流动阻力，且会造成管道进口堵塞及管内壁严重磨蚀[17]，所以颗粒体积分数α应不大于5%。

表1 流体物性参数

表2 模拟工况

1.2 数值模拟设置

使用Fluent软件对流体相进行数值模拟，选用基于压力瞬态求解器下标准k-ε湍流模型，选用近壁面增强壁面处理法处理。选用速度入口边界条件，压力出口边界条件定义出口静压为0，参考压力为101 325 Pa，管壁处设置恒定壁温为350 K，选择非滑移壁面边界条件。计算过程首先用一阶迎风格式的SIMPLE算法进行初始流场的稳态计算，然后在此基础上使用二阶迎风格式的PISO算法进行非稳态计算。

壁面与颗粒之间的参数参照文献[18-19]设置，见表3，颗粒材料为陶瓷，立式管材料为钢。颗粒相在EDEM软件中与颗粒、 壁面间均采用内置无滑移Hertz-Mindlin接触模型，重力方向为流体流动的相反方向。

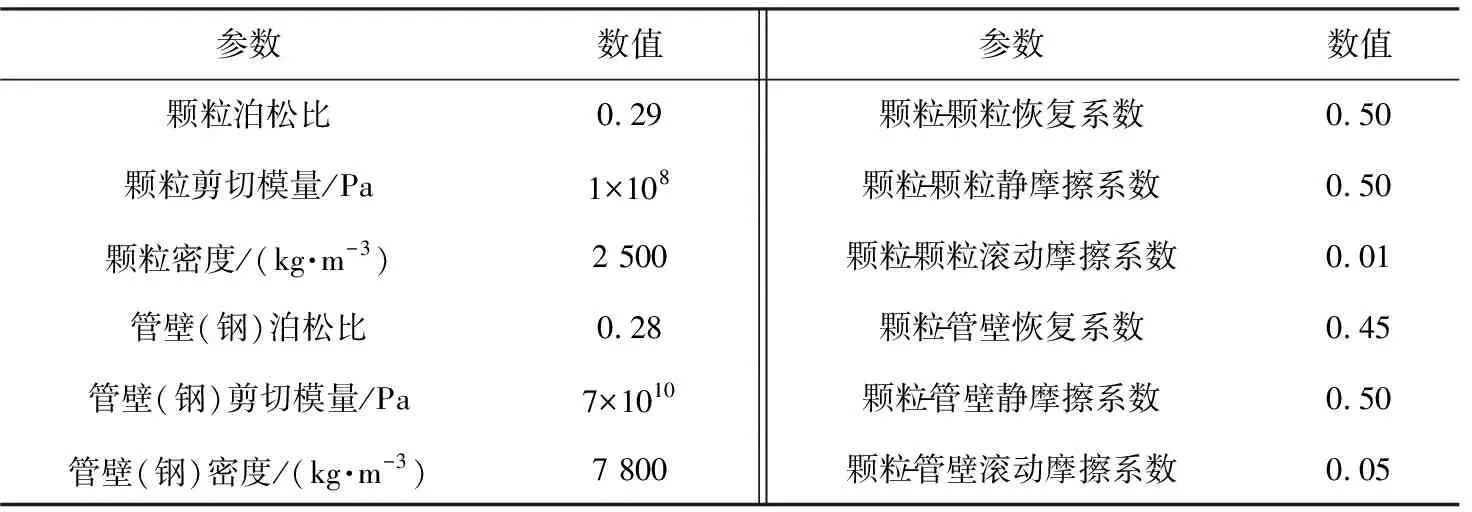
表3 壁面与颗粒参数

1.3 模型验证

为了验证CFD-DEM耦合方法可靠性，采用Shokri等[20]在相同雷诺数和浓度下不同粒径玻璃球颗粒实验结果进行对应建模及数值模拟。图4为颗粒流体在管道中心和管壁处的平均速度分布，其中，r表示管内任意位置到管中心的径向距离，R表示管的半径。模拟与实验的误差范围在7%～10%之间，认为误差可接受，说明在立式上行换热管内采用CFD-DEM耦合方法模拟椭球形颗粒运动是可行的。

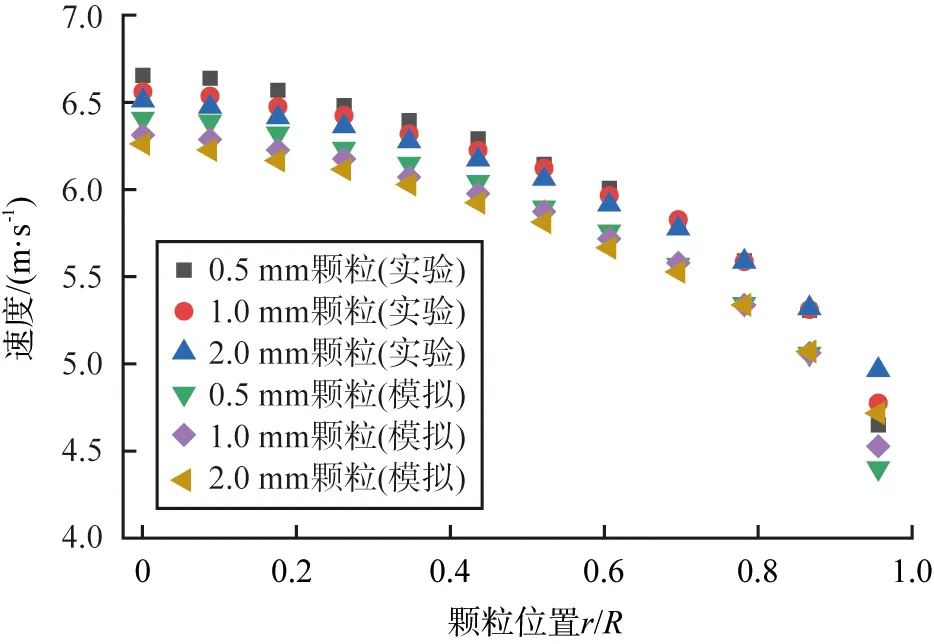
图4 数值模拟与实验结果对比图Fig.4 Comparison of numerical simulation and experimental results

2 结果与分析

2.1 颗粒分布位置周期性波动分析

为了研究在立式上行换热管内颗粒自下而上运动中颗粒位置分布，沿流体和颗粒运动方向，考虑颗粒自身尺寸，选取Z=(400±5)、 (800±5)、 (1 200±5)、 (1 600±5) mm等4个区域的颗粒位置信息。因为液固两相运动具有随机性，一定时间后管内会达到动态稳定，动态稳定的表现可以通过颗粒质量流量来观测。选取颗粒体积分数α=2%，长径比β=1.5的椭球形颗粒在监测段(Z=1 800～2 000 mm)内的质量流量随时间变化进行分析，结果如图5表示。由图可以观察到，t≥1.5 s后达到动态稳定，颗粒质量流量在一定数值范围内波动，选取波动曲线中的中轴线、波峰和波谷t1、t2和t33个时刻的颗粒质量流量进行研究。

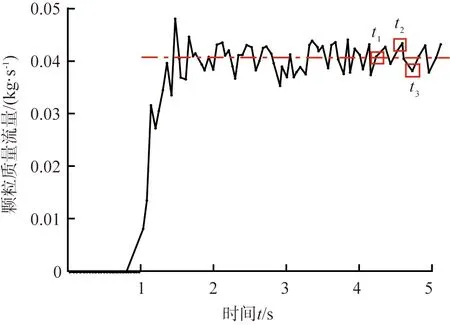
图5 质量流量变化图Fig.5 Change diagram of mass flow rate

图6—8分别为上述3个时刻的颗粒在立式换热管横截面(即XY平面， mm)上投影， 图中每一个圆点表示一个颗粒， 在Z=(400±5) mm区域， 在XY平面上颗粒分布较均匀， 颗粒进入Z=(800±5) mm区域，观察到近壁面区域颗粒增加，在Z=(1 200～2 000) mm颗粒运动后期，颗粒几乎堆积在管壁附近，管中心有少量零星颗粒，说明在颗粒随流体自下而上运动过程中，均匀进入管内颗粒逐渐受到流体作用向近壁面附近移动。选取周期不同时刻t1、t2和t3，颗粒在相同轴向位置变化趋势相同。动态稳定后的其他工况椭球形颗粒分布与图6—8相似，在此不一一阐述。

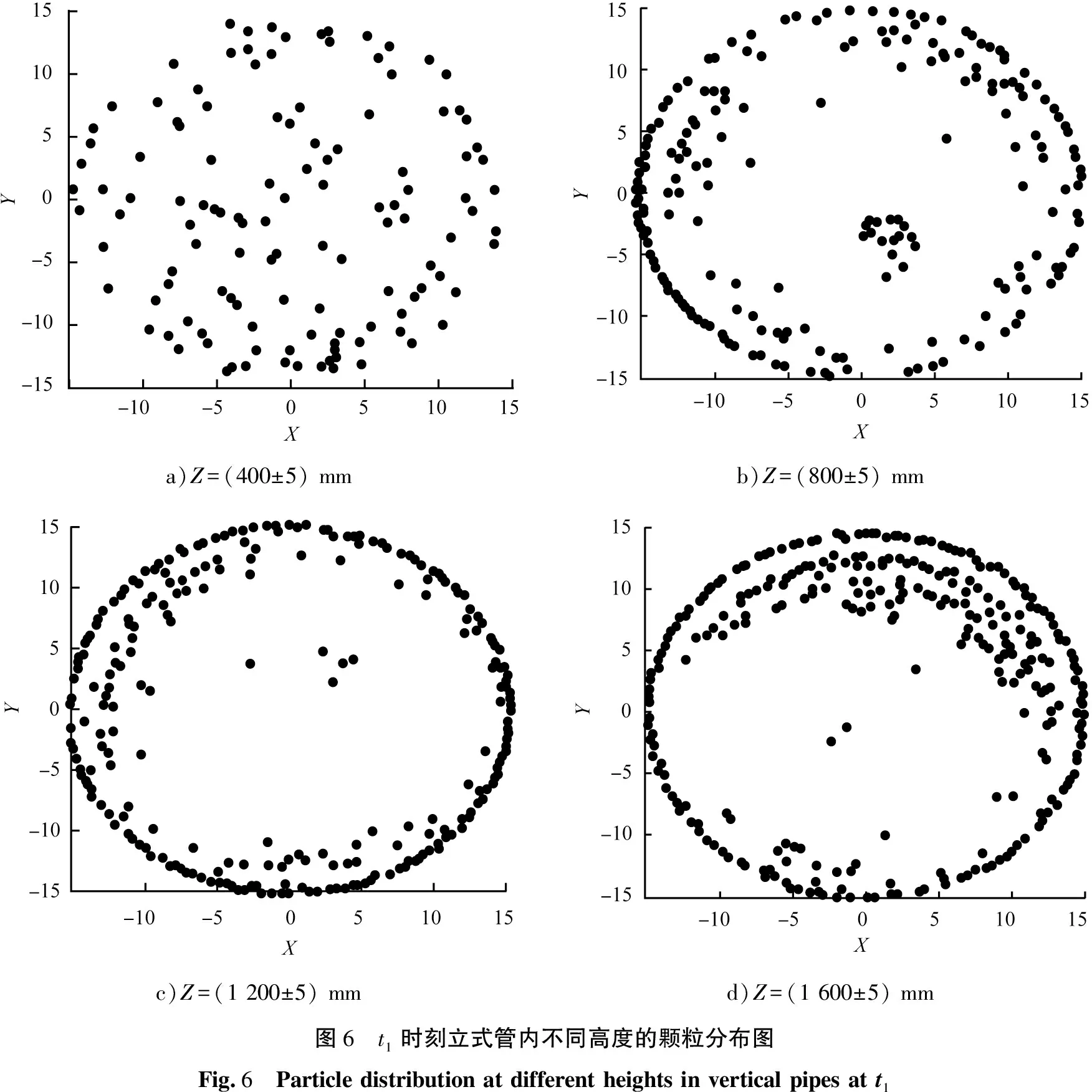
a)Z=(400±5) mmb)Z=(800±5) mmc)Z=(1 200±5) mmd)Z=(1 600±5) mm图6 t1时刻立式管内不同高度的颗粒分布图Fig.6 Particle distribution at different heights in vertical pipes at t1

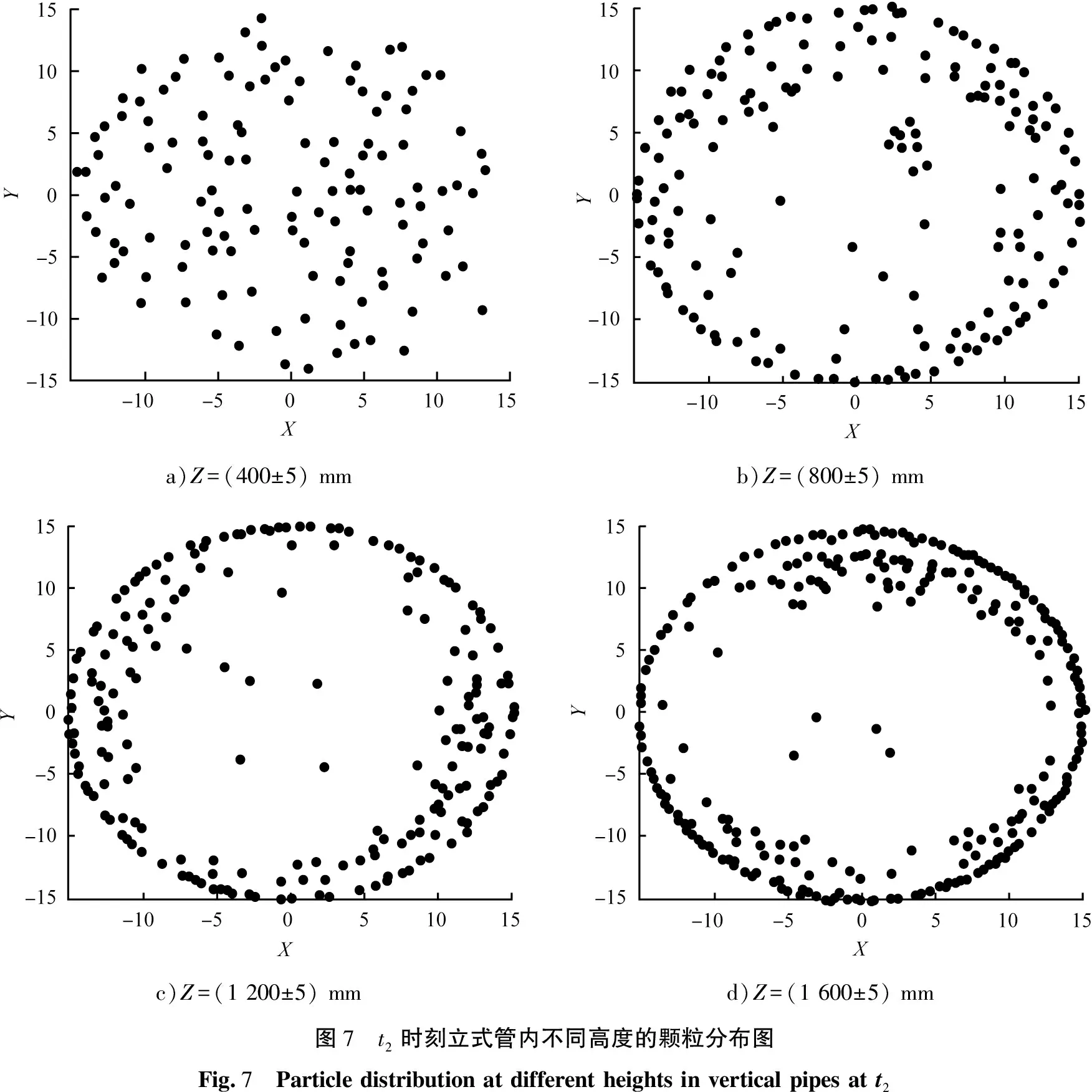
a)Z=(400±5) mmb)Z=(800±5) mmc)Z=(1 200±5) mmd)Z=(1 600±5) mm图7 t2时刻立式管内不同高度的颗粒分布图Fig.7 Particle distribution at different heights in vertical pipes at t2

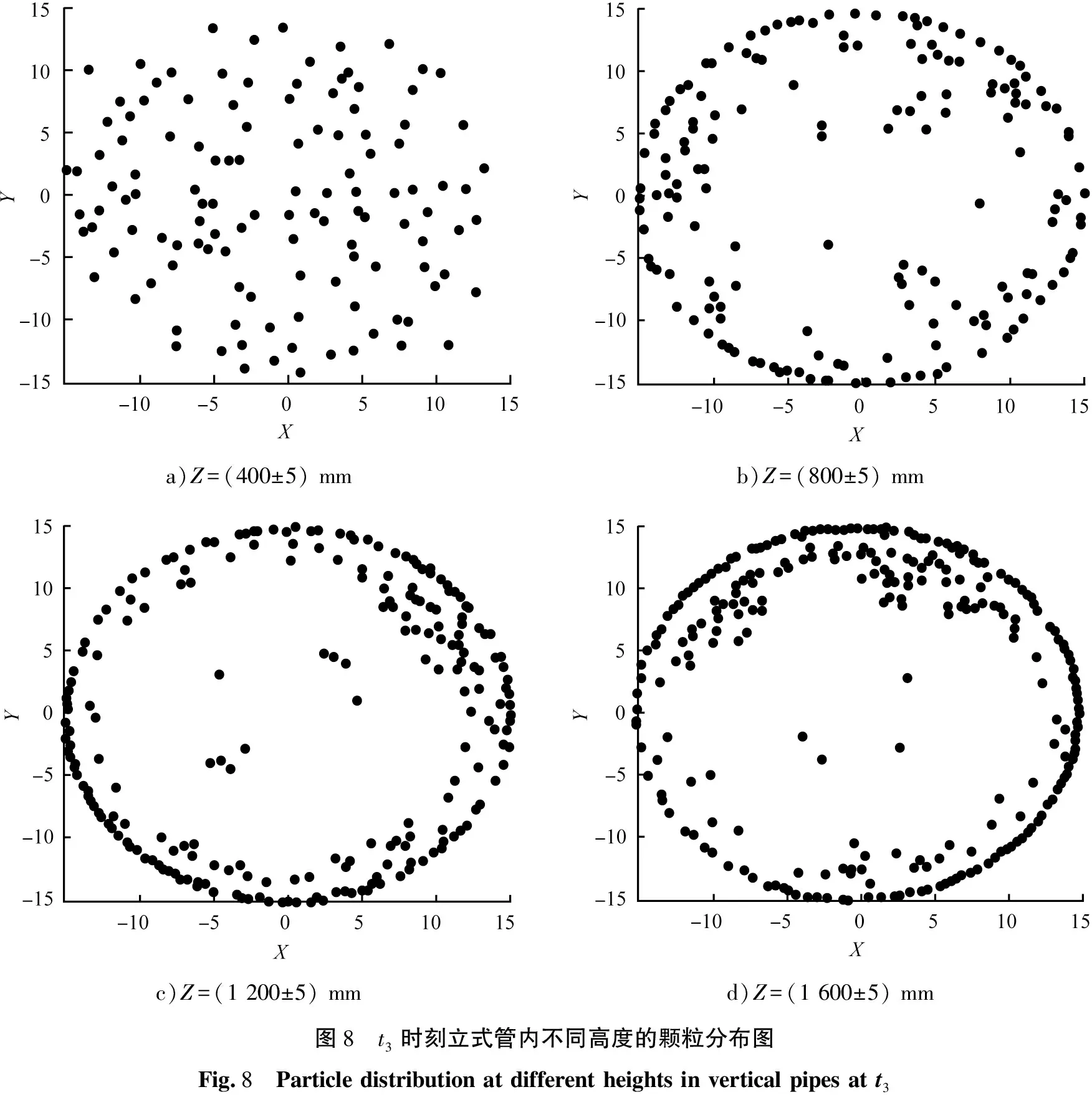
a)Z=(400±5) mmb)Z=(800±5) mmc)Z=(1 200±5) mmd)Z=(1 600±5) mm图8 t3时刻立式管内不同高度的颗粒分布图Fig.8 Particle distribution at different heights in vertical pipes at t3

2.2 颗粒径向相对体积分数分布分析

将立式换热管沿Z轴方向，以管圆心为中心选择7个不同半径(r=2、 4、 6、 8、 10、 12、 14 mm)的圆柱形区域，以此来研究经充分发展后换热管径向方向上颗粒相对体积分数变化规律(见图9)。对近壁面区域颗粒相对体积分数分布分析，由于颗粒自身体积较大，因此选择r=14 mm截面看作近壁面区域。

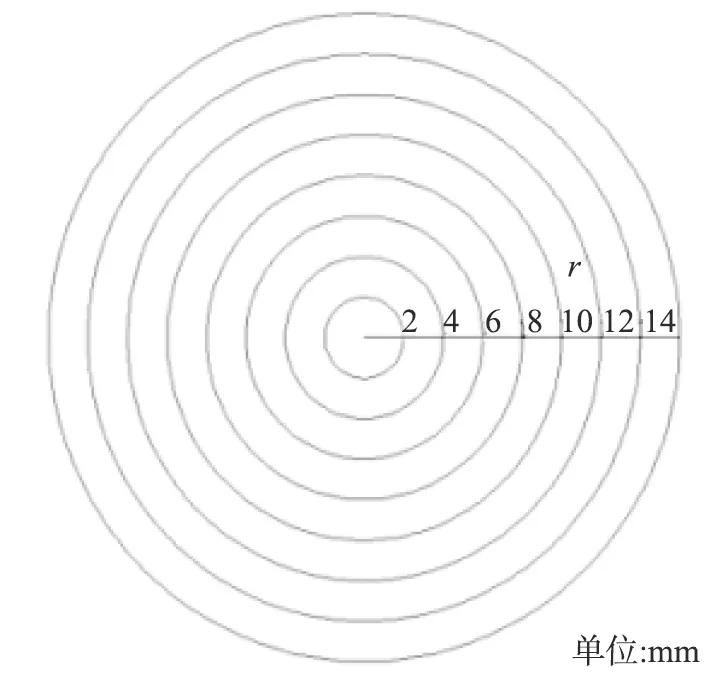
图9 区域划分示意图Fig.9 Diagram of regional division

图10为不同颗粒体积分数下的颗粒径向相对体积分数分布图。如图分析得到，1)经充分发展阶段后，径向方向上颗粒相对体积分数主要集中在近壁区域，管中心区域颗粒相对体积分数较低，说明立式管内颗粒受流体径向作用力影响发生迁移；2)在r为2～8 mm区域，颗粒相对体积分数变化不明显，而在r为8～14 mm区域，越靠近壁面区域，颗粒相对体积分数增加的幅度越来越大，这是由于绝大部分管中心颗粒受到流体的径向作用力，逐渐向管壁面做迁移运动，最终导致近壁面区域颗粒相对体积分数最大；3)在低颗粒体积分数(α=1%、 2%、 3%)时，颗粒相对体积分数在r为10～14 mm区域有较大的增长变化，而高颗粒体积分数(α=4%、 5%)中有较大增长的颗粒相对体积分数则提前至r为8～14 mm。观察图10中各曲线斜率可知，随着颗粒体积分数α由1%增长到5%，在r=10 mm处的曲线斜率越来越大，这是由于随管内颗粒数量越来越多，近壁面区域(r=14 mm)颗粒数量逐渐达到饱和，其他受到流体作用力的颗粒慢慢向r=10～12 mm区域堆积。

不同颗粒长径比β条件下，近壁区域(r=14 mm)颗粒相对体积分数随颗粒体积分数α变化如图11所示。由图可知，随着颗粒体积分数α增大，颗粒在近壁区域颗粒相对体积分数均呈上升趋势，但是增长速率逐渐变小。这是因为随着颗粒体积分数增加，进入管内颗粒数量变多，颗粒在流体径向力作用下向近壁面区域迁移，导致近壁面区域颗粒相对体积分数增大，然而，当近壁面区域处颗粒数量达到饱和时，颗粒相对体积分数值变化较小。

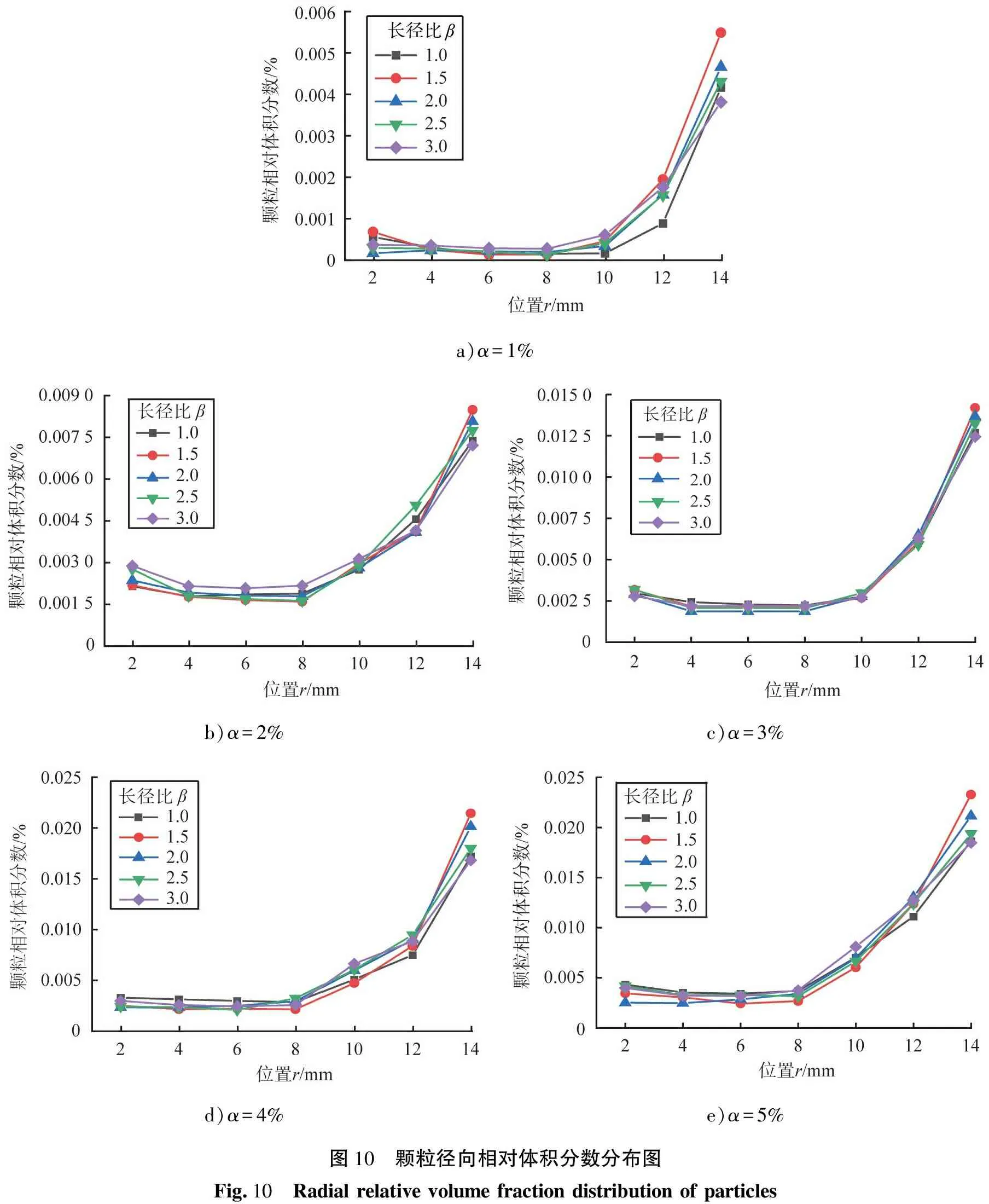
a)α=1%b)α=2%c)α=3%d)α=4%e)α=5%图10 颗粒径向相对体积分数分布图Fig.10 Radial relative volume fraction distribution of particles

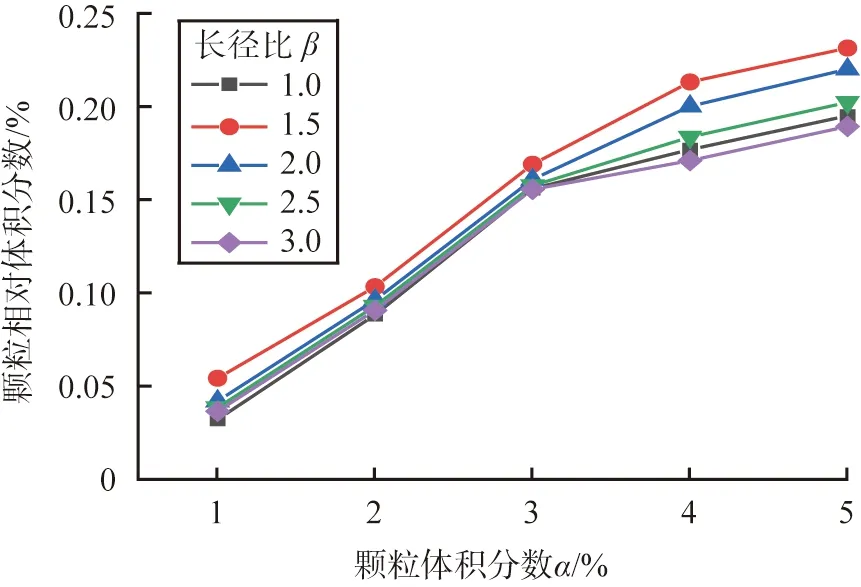
图11 截面r=14 mm处颗粒相对体积分数对比图Fig.11 Comparison chart of relative volume fraction of particles at section r=14 mm

长径比β=1.5的椭球形颗粒近壁区域相对体积分数最大，分别比β=1.0、β=2.0、β=2.5和β=3.0颗粒的提高16.43%、4.82%、11.72%和19.47%，说明近壁区域颗粒相对体积分数与椭球形颗粒长径比β有关。在低颗粒体积分数(1%～2%)，长径比β=1.0的球形颗粒与β=3.0的椭球形颗粒在近壁区域的颗粒相对体积分数值相差不大，随着颗粒体积分数增大(3%～5%)，球形颗粒相对体积分数大于β=3.0椭球形颗粒，说明椭球形颗粒在近壁区域内颗粒相对体积分数值并非恒大于球形颗粒。

2.3 颗粒跟随性分析

颗粒与流体在立式管内运动过程分初始段、过渡段和充分发展段，在充分发展段，颗粒与流体运动较为稳定。基于上述颗粒径向浓度分布，在充分发展阶段(Z=1 500～2 000 mm)，分别提取同一位置颗粒相和流体相瞬时轴向速度， 观察椭球形颗粒长径比对液固两相速度差的分布规律。 由于考虑颗粒具体尺寸， 所以颗粒参数在流体相应位置Y方向(Y=0 mm)增加一定厚度(Y=-3～3 mm)， 其他方向(X=-16～16 mm、Z=1 500～2 000 mm)的两相选取参数均相同。 采用r/R来表征液固两相位置信息。 在r/R=±1处(管内壁处)流体的速度为0， 而且无法得到该位置颗粒的速度信息， 为了研究同一时刻流体和颗粒的速度信息选择r/R=-0.95～0.95的径向范围。

根据图10颗粒径向浓度分布图可知，长径比β的颗粒体积分数变化趋势大致相同，因此选取β对径向浓度分布影响差异最小的α=3%工况进行分析。图12为椭球形颗粒长径比β对液固两相瞬时轴向速度分布的影响。

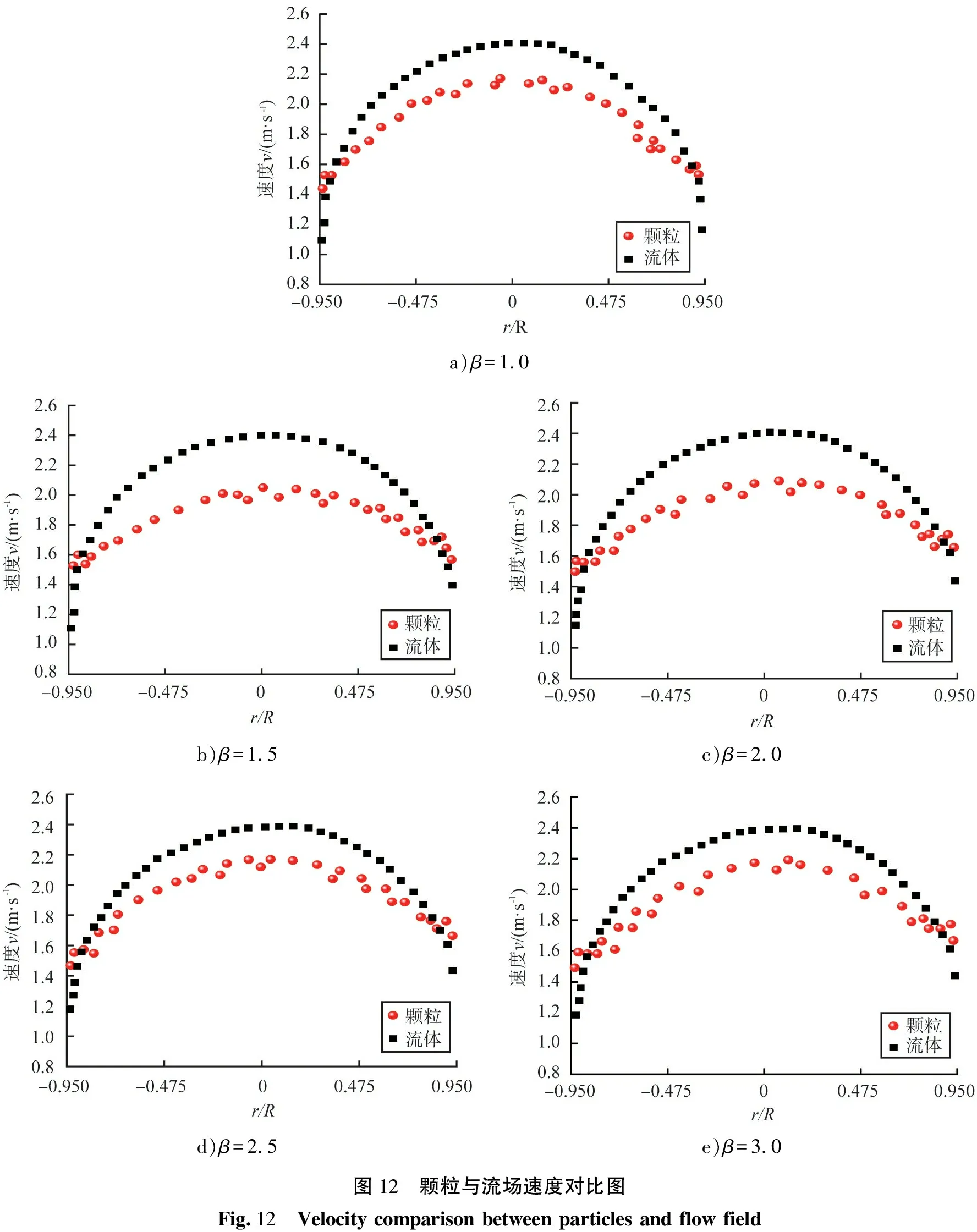
a)β=1.0b)β=1.5c)β=2.0d)β=2.5e)β=3.0图12 颗粒与流场速度对比图Fig.12 Velocity comparison between particles and flow field

由图可知，1)长径比β颗粒对流体沿径向方向的轴向速度分布不同，加入球形颗粒的流体轴向速度呈倒U形并呈管中心对称分布，加入β>1.0椭球形颗粒流体轴向速度分布并不严格对称，这也表明椭球形颗粒在流场中运动随机性更大；2)椭球形颗粒与周围流体速度差增大，说明椭球形颗粒在流体内速度波动程度更大，即椭球形颗粒在流体中有更活跃运动状态，从而降低了椭球形颗粒跟随流体同步运动能力。

为了更好表征椭球形颗粒长径比对颗粒跟随性影响，参照文献[21]定义滑移系数η进行量化评估。

η=Uf/Up，

(1)

式中：Uf为流体平均速度；Up为颗粒平均速度。

滑移系数η越大，表示周围流场与颗粒速度差越大。在近壁面处，流体满足无滑移边界条件，而颗粒与壁面碰撞有较大动量，导致在近壁面区域(r/R=-0.95～-0.7和r/R=0.7～0.95)颗粒速度大于流体速度，因此选择管中心主要区域(r/R=-0.7～0.7)对液固两相滑移系数分布规律进行研究。

将立式管自下而上按高度为200 mm划分为A—J等10个子流体区域，如图13所示。图14为上述工况下各子区域滑移系数变化，在立式管轴向中心区域，周围流体速度恒大于颗粒速度，即滑移系数η>1。 进入颗粒稳定运动阶段，β>1.0椭球形颗粒滑移系数始终大于球形颗粒，因为椭球形颗粒比球形颗粒在流体中的波动范围更大，其中β=1.5椭球形颗粒有最大的滑移系数，说明在流体运动中长径比β=1.5椭球形颗粒比其他颗粒更加活跃。

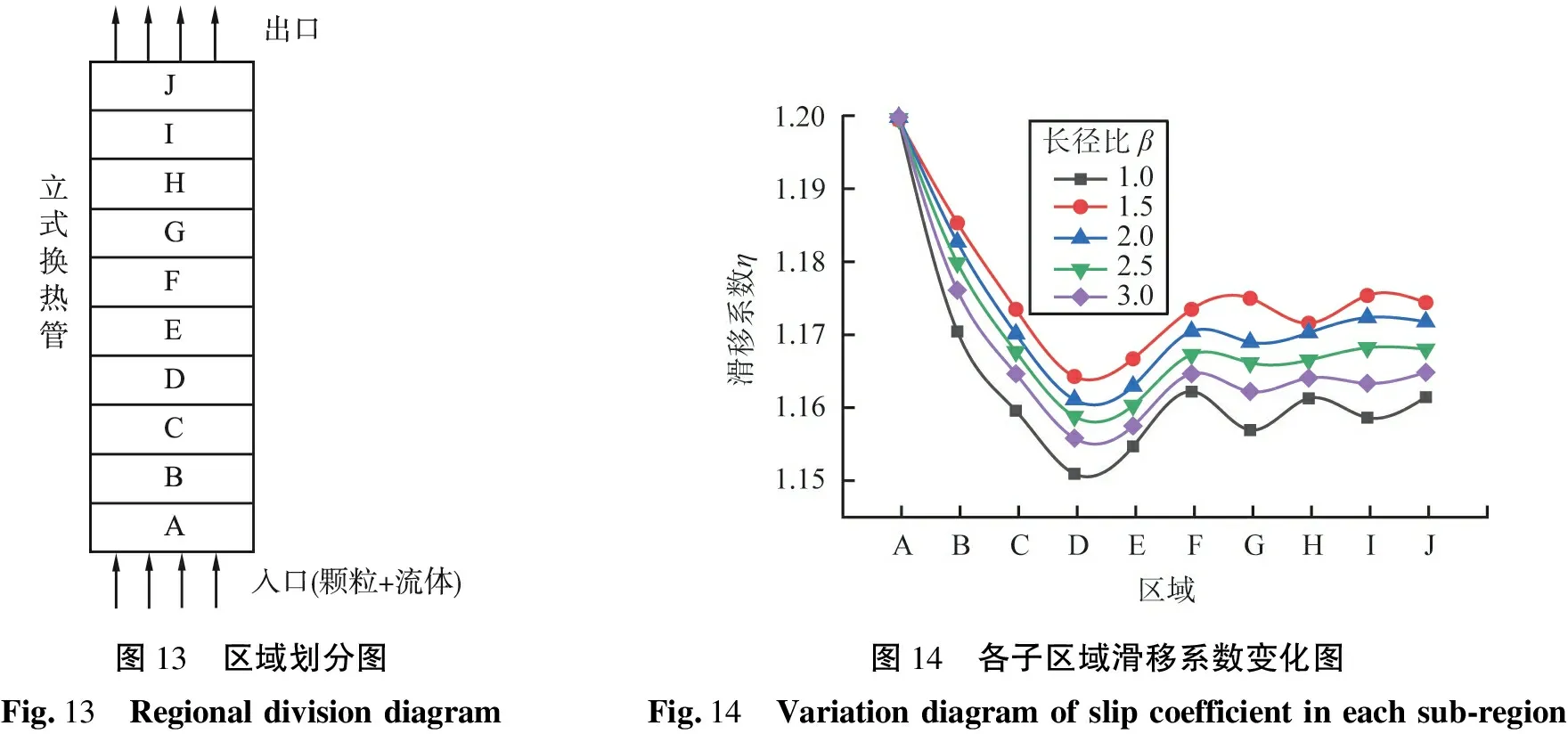
图13 区域划分图Fig.13 Regional division diagram图14 各子区域滑移系数变化图Fig.14 Variation diagram of slip coefficient in each sub-region

3 结论

采用CFD-DEM耦合方法研究了颗粒在立式换热管内分布与运动特性，得到如下结论。

1)在动态稳定周期内，横截面上颗粒径向分布在任意时刻均相似，颗粒在立式换热管下半部分横截面上较均匀，颗粒随着流体向上运动，管中心处颗粒数量逐渐减少；在换热管上半部分，管中心处几乎不存在颗粒，颗粒主要分布在管壁附近。

2)经充分发展阶段后，颗粒相对体积分数沿径向方向逐渐增加，管中心颗粒数量较少且变化不大，随着颗粒体积分数增加，近壁区域颗粒相对体积分数先逐渐增大，达到饱和后趋于稳定。颗粒体积分数α为1%～3%时，颗粒相对体积分数明显增长位置在r=10～14 mm区域，颗粒体积分数α为4%～5%时有明显增长的颗粒相对体积分数位置则提前至离管中心较近的r=8～14 mm区域。长径比β=1.5椭球形颗粒在近壁区域的相对体积分数最大，但椭球形颗粒在近壁区域内颗粒相对体积分数值并非恒大于球形颗粒。

3)截面上颗粒和流体速度均呈现倒U型近似轴对称分布，在r/R=-0.7～0.7的管内截面区域周围流体速度均大于颗粒速度；在靠近壁面区域流体速度小于颗粒速度；椭球形颗粒滑移系数均大于球形颗粒的，其中β=1.5椭球形颗粒的滑移系数最大。