基于最小外接矩形和Hough变换的定位算法*

黄 超，茅 健，徐 斌，周玉凤

(上海工程技术大学机械与汽车工程学院 ，上海 201620)

0 引言

随着“中国制造2025”的提出，智能制造逐渐成为制造技术发展的核心方向[1]。装配机器人是柔性自动化生产系统中的核心环节，新一代表面贴装生产线逐渐应用搭载了视觉系统的装配机器人完成工件抓取和装配任务。工件传输过程中易发生位置偏移，机器人若无法及时更新工件位置信息，执行预定动作将会造成任务失败。研究高效精确的工件识别与定位算法，一直受到国内外学者的广泛关注。

目前，将图像处理[2]、机器视觉[3]、深度学习[4]等方法应用到机器人工件识别与定位的案例有很多。李致金等[5]采用主轴法对工件轮廓快速识别，该方法计算工件旋转角度时需经过复杂的求解中心距和归一化过程，耗时较长。李培丰等[6]基于分水岭算法计算工件位置，再利用Harris角点检测法计算工件旋转角度，此方法中分水岭需人工标注，Harris法筛选角点也存在漏点和误判的问题。武洪恩等[7]采用八邻域跟踪算法提取工件轮廓，使用Hu矩识别工件，再利用递进Hough变换法定位工件。寸毛毛等[8]利用改进后的Hu矩拟合工件外轮廓矩形实现定位，该方法通过去掉不变矩的比例因子、增加离心率特征改进Hu矩，增强了轮廓识别能力。卢军等[9]基于九点标定法对机器人进行标定，然后采用加权最小二乘法拟合工件亚像素边缘，再根据二维测量法定位工件，此方法鲁棒性强、提取工件边缘的精度高。张展等[10]采用最小外接矩形法分割出工件区域，再利用RBF核支持向量机训练识别工件，该方法首先增强图像前景与背景的对比度，再分割出目标，分割准确度高。

本文针对表面贴装自动生产线中工件定位与偏移量计算问题，提出了一种基于最小外接矩形和Hough变换的工件定位算法，采用格雷厄姆法和凸壳边界旋转法求解目标最小外接矩形，结合图像矩定位工件，然后通过Hough变换法计算工件旋转角度，降低了计算量，提高了定位精度。

1 工作原理与算法流程

机器人视觉装配系统如图1所示，由机器人控制系统、视觉系统两部分组成。机器人末端挂载视觉相机用于采集图像，工控计算机负责机器人运动控制和图像处理。机器人需执行的任务：抓取右侧PCB工件装配于左侧载具中，然后将其整体投入产线中。

图1 机器人视觉装配系统

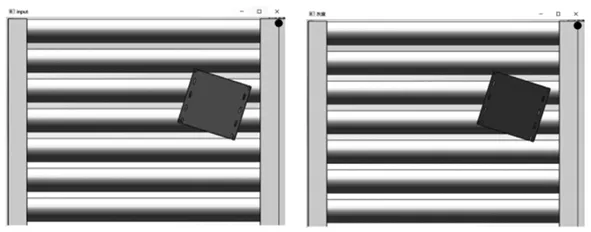
工件传输过程中发生位置偏移如图2所示，PCB工件和载具均发生了位置偏移和角度偏转，机器人若无法及时校正位置矢量，执行任务将会失败。要实现机器人对工件位置矢量的自动校正，需解决3个问题：①定位工件，计算中心像素坐标(u,v)；②计算工件旋转角度θ和偏移量Δθ；③计算工件像素偏移量Δu、Δv，并转换成机器人末端坐标系下的偏移量Δx、Δy。

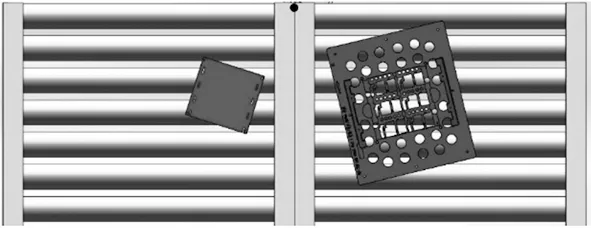
图2 工件位姿偏移图像

算法流程如图3所示，机器人在抓取目标前，首先通过视觉系统采集工件图像，对图像进行预处理：包含灰度化、阈值分割使前景和背景分离，中值滤波去除图像中零散像素点，Canny算子提取目标物边缘，膨胀处理增强目标物特征信息等一系列操作。再利用本文算法计算出工件中心像素坐标和旋转角度，通过对比标定工件得到新工件的偏移量Δu、Δυ、Δθ，再将Δu、Δυ、转换成Δx、Δy，最后将Δx、Δy、Δθ发送给机器人控制器，机器人就能对工件位置进行自动校正，以适应环境变化。

图3 算法流程图

2 工件定位算法

2.1 视觉系统标定

如图4所示，{O0X0Y0Z0}为机器人基坐标系、{OeXeYeZe}为末端执行器坐标系、{OcXcYcZc}为视觉相机坐标系、{OgXgYgZg}为工件图像坐标系，如式(1)需要求解工件像素坐标(u,v)映射到{OeXeYeZe}坐标(Xe,Ye,Ze)的变换矩阵T。

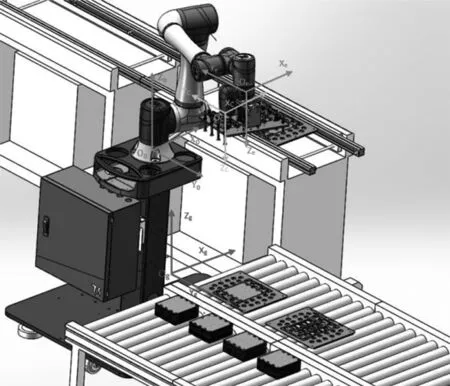
图4 坐标系

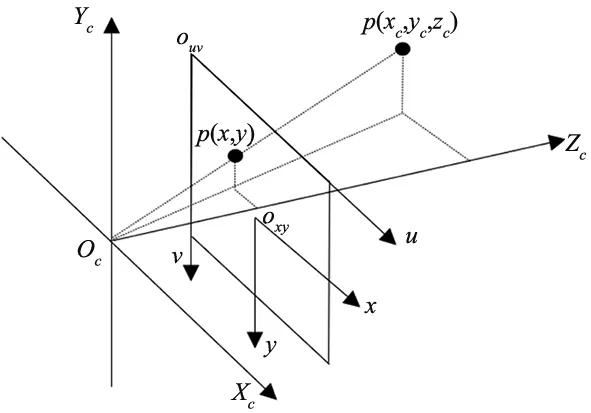
图5 针孔成像模型

(1)

已知：像素坐标(u,v)与图像坐标(x,y)的变换式、图像坐标(x,y)与相机坐标(Xc,Yc,Zc)的变换式、相机坐标 (Xc,Yc,Zc)与末端执行器坐标(Xe,Ye,Ze)的变换式[11]：

(2)

可推导出像素坐标(u,v)与末端执行器坐标(Xe,Ye,Ze)的映射表达式如下：

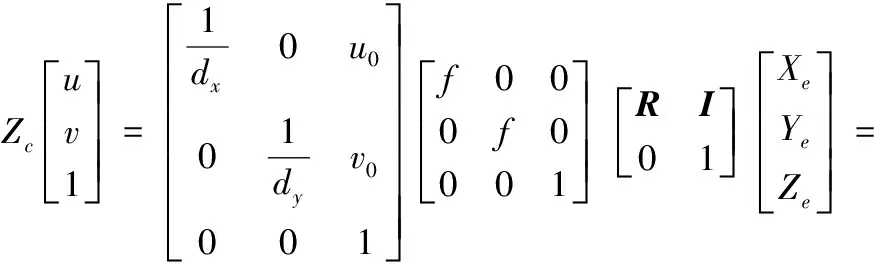
(3)

从而得到变换矩阵T：

(4)

其中，fx、fy、u0、v0是相机的内参数，R(3×3的正交矩阵)、I(平移矩阵)是相机的外参数。这些相机的内外参数，可通过采集不同方向的黑白棋盘格图像进行标定求解。

2.2 图像预处理

在工件图像采集过程中，由于现场环境、光照强度、相机抖动等因素都会影响图像质量，为了减少图像中干扰信息，增强目标特征信息，需对原图像进行预处理，处理流程如图6所示。

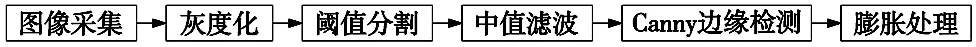
图6 图像预处理

(1)灰度化，彩色图像增加了图像处理时间[12]，而灰度图像与彩色图像具有同等特征描述，灰度化效果如图7所示。

(a) 彩色图 (b) 灰度图

(2)阈值分割，由于工件为绿色，标识物为黑色，运输机滚筒为白灰金属色，为了避免背景对工件特征识别的影响，需对背景区域与目标区域进行分割。设阈值为T，采用阈值化取反[13]如式(5)进行分割。分割后图像如图8a所示，背景滚筒已被大部分过滤掉，只剩下少许边界线。

(5)

式中,f(x,y)为图像的灰度值，B(x,y)为分割后图像的像素值。

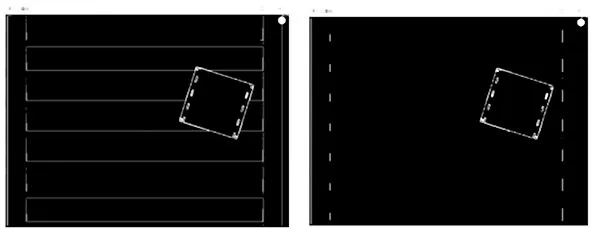
(a) 未滤波 (b) 滤波后

(3)中值滤波[14]，为了进一步祛除图像中滚筒边界线等噪声，采用中值滤波方法，效果如图8b所示，背景中滚筒边界线被视为噪声祛除了。

(4)Canny[15]边缘检测，提取出图8b中的清晰边缘线，如图9a所示，目标物边界线间断不连续且特征不明显。

(a) Canny边缘图像 (b) 膨胀后的边缘图像

(5)膨胀处理，增强目标边界线特征，对图像进行膨胀处理，则可得到清晰的轮廓边界线，效果如图9b所示。

2.3 基于最小外接矩形的定位原理

2.3.1 图像矩

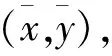
(6)

2.3.2 最小外接矩形求解原理

首先利用格雷厄姆算法求解目标图像的凸壳点集：

(1)如图10a先找到点集中纵坐标最小的点P0，与其它点分别连接得到线段集Lp，计算Lp中各线段长度和与X轴正向夹角，按夹角和线段长度由小到大对点编号(P1,P2,…Pn)；

(2)判断除Pi,Pi+1点之外的所有点是否分布于线段PiPi+1(i=0,1,…,n-1)的同一侧，若满足则继续选取下一条线段进行判断，若不满足则抛弃当前线段的末端点Pi+1，将后面的点Pi+j(j=2,3,…,n)作为新的末端点，连接线段PiPi+j再进行判断直到满足为止。依此规律可得到最终的凸壳边界和顶点集W={P0,P1,P3,P6,P8,P9}如图10a所示。

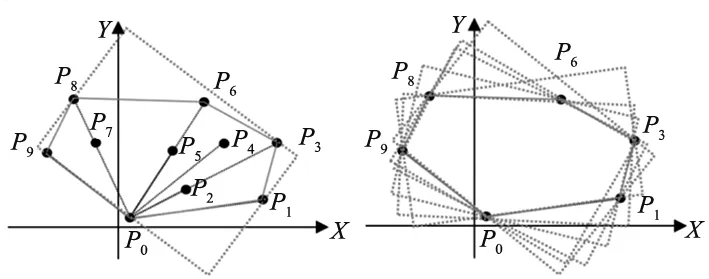
(a) 平面点集 (b) 边界旋转

再通过边界旋转确定最小外接矩形：

(1)如图10b根据W点集分别找到X轴和Y轴方向上坐标最大最小点，则可得到初始最小外接矩形Rect0，记录Rect0的面积和四顶点位置。

(7)

特别地，当目标外轮廓为矩形时，那么所有凸壳边界旋转后的外接矩形都是相同的，因此计算过程可简化为：得到凸壳边界顶点集W后，找到X轴和Y轴方向上坐标最大最小点，初始最小外接矩形Rect0即为最终所求。

2.3.3 筛选目标

利用凸壳边界旋转法检测得到所有轮廓的外接矩形见图11a，由于图像预处理后图9b中仍然残留少许无效特征，且工件表面也存在工艺槽等轮廓，导致图11a中出现许多矩形，因此还需筛选出工件和标识物的轮廓外接矩形。

本文引入2个筛选变量：

②外接矩形的面积area。经多次调参实验，发现当ratio>0.9且area>100时，可筛选出目标的轮廓外接矩形如图11b所示。提取到目标外接矩形后，利用式(6)中的重心公式可计算出外接矩形区域的中心坐标。

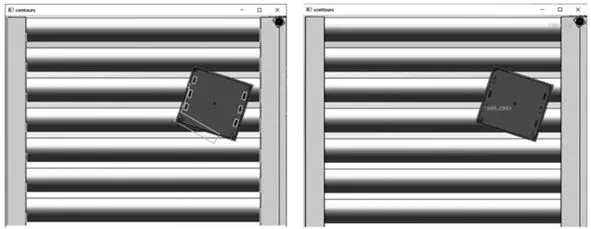
(a) 所有轮廓的外接矩阵 (b) 目标轮廓的外接矩阵

2.4 基于Hough变换的旋转角度计算

虽然利用式(6)(主轴法)也可计算出目标的旋转角度，但求解中心距μpq、归一化、再求解主轴方向角θ的计算过程比较复杂且运算量大，可能无法满足机器人作业的实时性要求。因此本文提出基于Hough[16]变换的方法计算旋转角度，具体步骤如下：

(1)首先通过Hough变换，检测出工件图像中所有直线如图12a所示，构成集合LN={L1,L2,L3,…,Ln}。

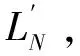
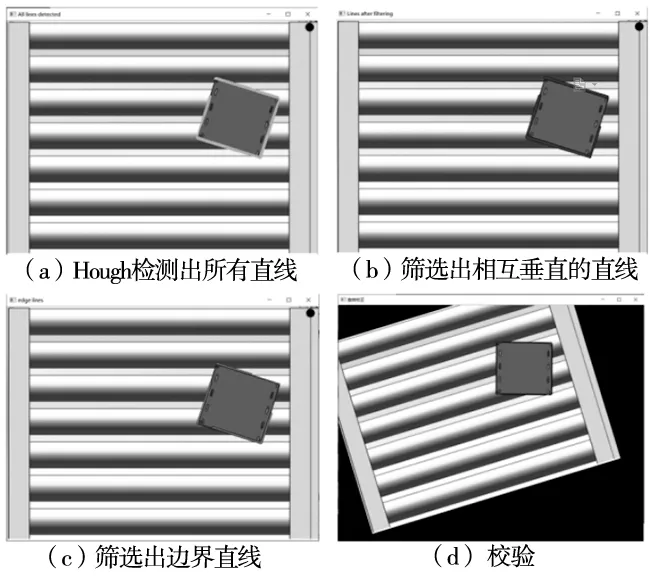
图12 Hough法求旋转角度

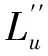
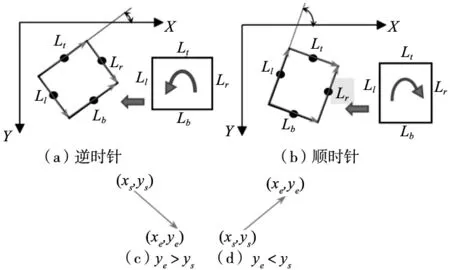
图13 边界直线

(8)

(9)

(10)

(5)校验旋转角度，将图像按θ的逆方向旋转图像如图12d所示，检验图像中边界直线Ll,Lr与X是否垂直，来判断旋转角度的准确性。

2.5 工件偏移量的计算

(1)首先计算标定工件的像素坐标：标识物中心像素坐标为(u1,v1)，标定工件中心像素坐标为(u2,v2)，则标定工件在{OgXgYgZg}下的坐标为(u2-u1,v2-v1)，标定工件的旋转角度为θ1；

(3)最后计算偏移量，式(11)可计算出像素偏移量Δu、Δv以及旋转角度偏移量Δθ，式(1)的等价公式(12)可将Δu、Δv转换为坐标系{OeXeYeZe}下的偏移量Δx、Δy，Δθ无需转换。

(11)

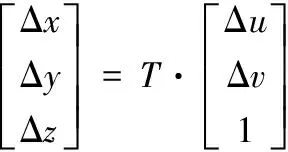
(12)

3 实验验证与结果分析

3.1 仿真实验

将工件随机摆放于运输机任意位置，利用本文算法计算工件中心坐标和旋转角度，通过式(11)、式(12)计算偏移量Δx、Δy、Δθ。利用SolidWorks中卷尺工具实际测量偏移量Δx*、Δy*、Δθ*，此外，为了评估Hough法和主轴法求解旋转角度的性能差异，利用主轴法计算偏移量Δθ′，作为对比，共进行了50次仿真实验，部分结果如图14所示。

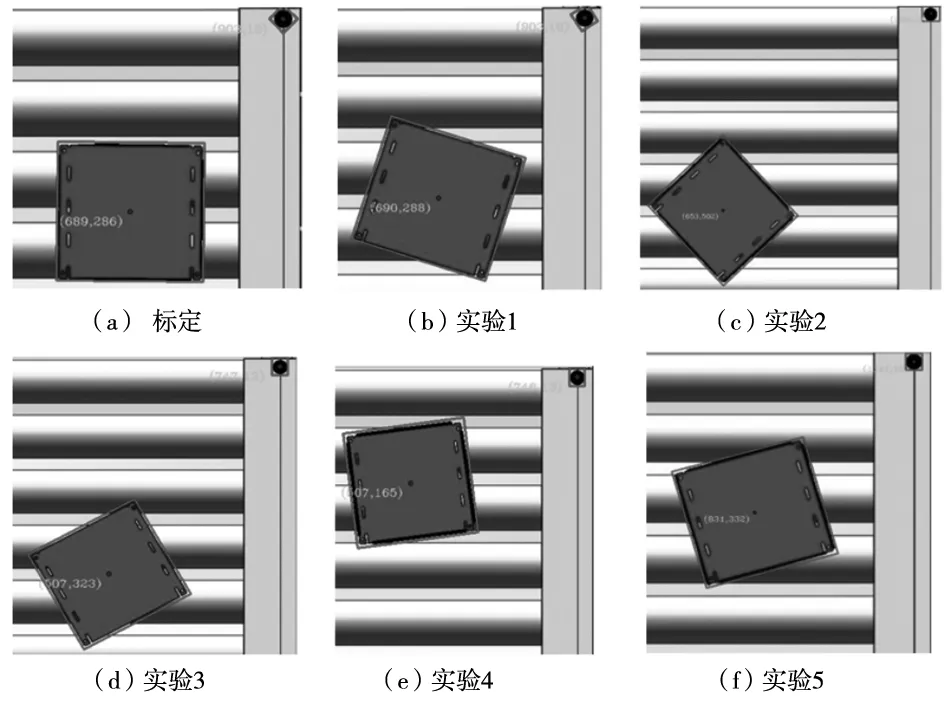
图14 部分仿真实验

(1)评估计算误差

用式(13)计算偏移量的误差δx、δy、δθ、δθ′，得到δx与δy的曲线如图15a所示，δθ与δθ′的曲线如图15b所示。由图15a可知δx、δy的波动范围为[-0.5,+0.5]，由图15b可知δθ的波动范围为[-0.2°,+0.2°]，δθ′的波动范围为[-0.5°,+0.5°]，均能满足系统定位精度要求(位置误差≤1 mm ，角度误差≤1°)，并且使用Hough法求解旋转角度的误差小于主轴法。

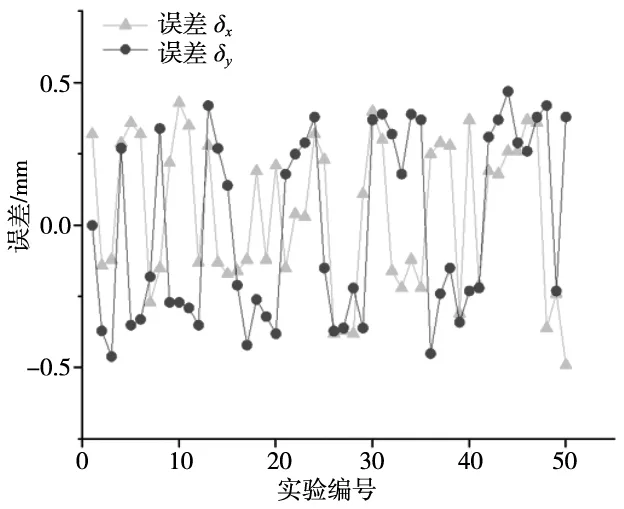
(a) δx与δy

(b) Hough法δθ与主轴法δθ′图15 误差曲线

(13)

(2)评估算法时间性能

分别使用Hough法和主轴法计算旋转角度，统计50次实验的运行时间，由图16可知，Hough法的平均求解时间约为1 140.44 ms,主轴法的平均求解时间约为1 751.44 ms,Hough法的平均求解时间约为主轴法平均求解时间的65%，提高了计算效率。

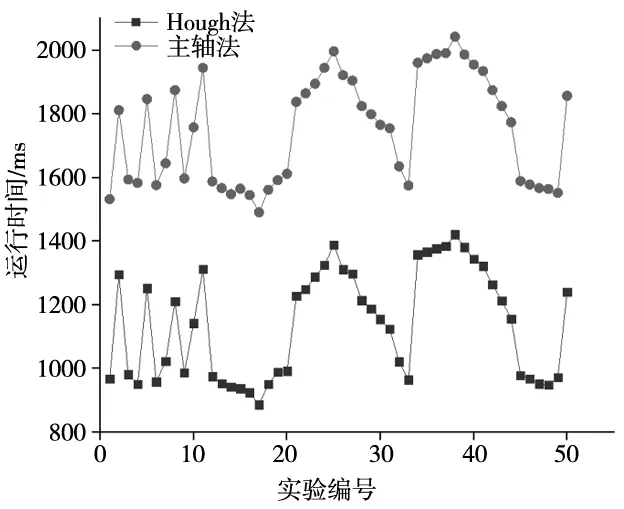
图16 时间性能

3.2 真机实验

将本文算法应用到达明机器人视觉装配系统，测试自动校正效果。如图17所示。抓取工件PCB、装配到载具、投入产线。现场测试结果表明，搭载有视觉系统的机器人能很好的适应工件位姿偏移、工件尺寸规格不同、载具位姿偏移等各种工况，抓取和装配成功率高，证明了本算法的有效性。

图17 真机实验

4 结论

(1)针对表面贴装自动生产线中矩形工件的定位与偏移量校正问题，本文提出了一种基于最小外接矩形和Hough变换的定位算法，该算法适用于不同尺寸的矩形工件。

(2)仿真实验结果表明，本文算法的位置误差和角度误差均能满足定位精度要求，且证明了Hough法比主轴法计算精度高且计算时间缩短了约35%。实际生产结果表明，移植了本文算法的视觉机器人能更精确地完成工件抓取和装配任务，证明了算法的实用性。