基于四元数乘法可易性的机器人手眼标定算法*

吴庆华，李子奇，李宗耀，邱捷锋

(湖北工业大学 a.机械工程学院；b.现代制造与质量工程湖北省重点实验室，武汉 430068)

0 引言

机器人视觉引导系统被广泛应用于工业领域，该系统的关键问题是求取机器人工具坐标系和视觉坐标系之间的转换关系，可以用齐次矩阵描述这种关系[1]，如何快速准确地求取齐次矩阵是问题的核心部分。文献[1-2]最早提出AX=XB手眼标定模型，由于四元数可以方便地描述刚体旋转运动，文献[3]提出了基于四元数的求解算法，该算法步骤复杂，要求机器人末端执行器的旋转角θ≠360°n(n=0,1,...)；文献[4]基于矩阵奇异值分解求解手眼标定方程，其算法简洁但旋转角θ依然受到限制。在手眼标定的实际应用中，需要依据旋转角θ判断测量数据是否可以用于标定，使得标定过程复杂化。

针对上述问题，本文提出一种基于四元数乘法可易性的手眼标定方程新解法，通过四元数乘法可易性改写旋转矩阵，再结合矩阵奇异值分解筛选求解旋转矩阵，使旋转角θ不受限制，之后代入求解平移向量，最后通过仿真和验证实验，检验该方法准确性和鲁棒性。

1 机器人手眼标定问题描述

机器人手眼系统主要分为Eye-in-Hand系统和Eye-to-Hand系统，由于在Eye-in-Hand系统中，摄像机被固定在机器人末端执行器上，可以随机器人同时运动，因此被广泛用于工业生产当中[5]。为求解AX=XB类型手眼标定方程，可将方程展开如下:

(1)

其中，RA、RX和RB分别表示齐次变换矩阵A、B和X的旋转部分，tA、tX和tB分别表示对应变换矩阵的平移部分，将式(1)再次展开可得：

(2)

基于四元数和矩阵奇异值分解的传统手眼标定方法[3-4]通过四元数改写旋转矩阵方程为Cx=0的形式后，通过欧拉参数[θ,uT]和单位四元数向量p=[e0,e1,e2,e3]T之间的转换关系，将旋转矩阵方程整理得到下式：

(3)

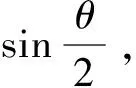
2 四元数乘法可易性手眼标定方法

2.1 四元数乘法可易性

单位四元数可以用来描述刚体在三维空间中的旋转变换[3]，设p和q分别表示两个描述三维旋转运动的单位四元数，其乘法可易性[6]描述如下:

p·q=M(p)·q=M(q)+·p

(4)

(5)

(6)

其中，M(q)+称为蜕变矩阵。

2.2 最小奇异值筛选求解旋转矩阵RX

对于Cx=0形式的超定方程[7]，对系数矩阵C进行奇异值分解即C=UΣVT时，x的最优解为右奇异矩阵V中最小奇异值所对应的列向量。在传统方法中，在对系数矩阵进行奇异值分解后，直接通过最小奇异值对应的列向量求取单位四元数，再求解旋转矩阵。由于在仿真和实际应用中，无法保证测量数据构成的系数矩阵直接进行奇异值分解时一定可以得到较好的结果，本文采用一种组合测量矩阵筛选最小奇异值的求解方法。

将式(3)描述旋转部分的方程RARX=RXRB使用四元数乘法进行表示，设a、b和qx分别表示旋转矩阵RA、RB和RX所对应的单位四元数，则旋转部分方程描述如下：

a·qx=qx·b

(7)

利用四元数乘法可易性将上式展开，整理移项后得到：

(8)

由于求解该方程时，机器人末端执行器至少需要改变n(n≥2)次位姿[1]，设S(n)=(M(an)-M(bn)+)为第n次测量结果所对应的4×4形式矩阵，求解旋转矩阵的伪代码如下所示：

输入：处理后的测量矩阵S(1)，S(2)……S(n)(n≥2)

初始化：k=0

1:fori=2→ndo

3: form=1→jdo

4:k=k+1

5: 构造系数矩阵T(k)=[M(1),M(2),……,M(i)]

6: end for

7:end for

8:对T(k)进行奇异值分解，将每次奇异值分解得到的最 小奇异值记为P(k)

9:用P(k)的最小值P(k)min对应的特征向量v，求解对

应单位四元数qx

10:用单位四元数qx求解旋转矩阵Rx

输出：旋转矩阵Rx

2.3 求解平移向量tX

将(2)中的平移向量方程RAtX+tA=RXtB-tA改写为如下形式：

(RA-I)tX=RXtB-tA

(9)

通过改变机器人末端执行器的位姿进行n次测量后，将之前求解得到的旋转矩阵RX代入计算，令

(10)

通过最小二乘法可以求得平移向量tX=(DTD)-1DTE。

3 实验结果与分析

3.1 仿真实验结果及分析

由于在机器人末端执行器旋转角θ=360°n(n=0,1,...)时，传统方法无法直接进行求解，因此仿真实验的主要目的是验证本文方法的准确性和鲁棒性，采用了处理器主频为2.6 G，内存为8 G的计算机进行仿真实验，仿真软件为MATLAB R2016b，仿真实验及数据处理步骤如下：

(1)依据文献[8]，假定机器人手眼关系X的真值为：

(2)随机生成n个正交矩阵RA1,RA2,…,RAn和平移向量tA1,tA2,...,tAn，分别组成转换矩阵A1,A2,...,A3，通过方程AX=XB求解对应变换矩阵B1,B2,..,Bn的旋转部分RB1,RB2,...,RBn和平移部分tB1,tB2,...,tBn。

(3)基于文献[9]的方法，为模拟实际测量情况，在模拟数据中加入高斯噪声(Gaussian Noise)，对RAi和RBi添加均值为0，标准差为0.01d的高斯噪声；对tAi和tBi添加均值为添加均值为0，标准差为0.2d的高斯噪声，其中d代表噪声水平。

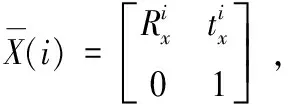
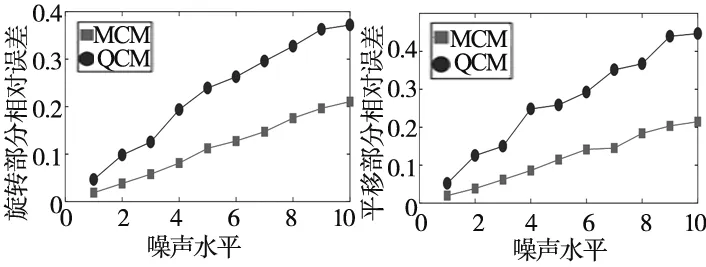
(a)相对旋转误差 (b)相对平移误差

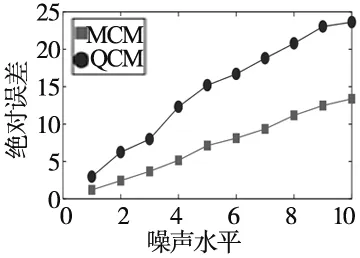
(c) 绝对误差图1 仅对A添加噪声

(a)相对旋转误差 (b)相对平移误差

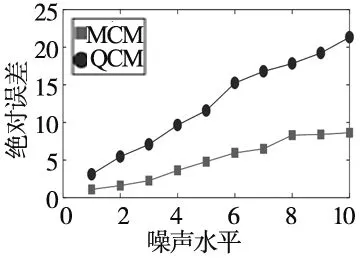
(c)绝对误差 图2 仅对B添加噪声

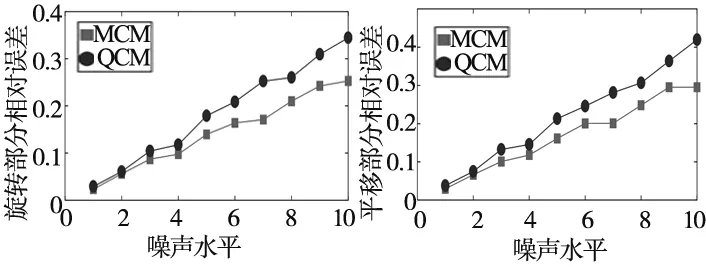
(a)相对旋转误差 (b)相对平移误差

(c)绝对误差图3 同时对A和B添加噪声

从图中可以看出，所提算法在噪声水平相同的情况下，准确性优于文献[4]所提出的求解方法，并且随着噪声水平的增大，本文算法依旧具有较好的鲁棒性。

3.2 手眼标定实验

图4 实验平台照片

为验证本文算法在实际应用中的可行性和准确性，使用FANUC公司的LR Mate 200iD型工业机器人、Basler公司的acA1600-20gm型工业相机和尺寸为100 mm×100 mm的棋盘格标定板进行验证实验，搭建的实验平台与如图4所示。

其中，FANUC工业机器人的重复定位精度为±0.02 mm,Basler工业相机的分辨率为1626×1236 pixels，像元尺寸为4.4 μm×4.4 μm，镜头焦距为25 mm，使用连接件将相机和工业机器人的法兰盘紧固在一起。

实验流程如下：

(1)移动工业机器人带动工业相机在10个不同位姿下对棋盘格标定板进行拍照，记录各位姿下机器人控制器的6个读数(x,y,z,w,p,r)并改写成对应的齐次转换矩阵(P1,P2,...,P10)，该矩阵描述了机器人法兰中心的工具坐标系和机器人基坐标系之间的坐标转换关系。

(2)对采集的10张图像使用MATLAB视觉工具箱进行标定相机内外参数的标定，如图5所示，得到10个不同位姿下的相机外参矩阵(Q1,Q2,...,Q10)。

图5 相机内外参数标定示意图

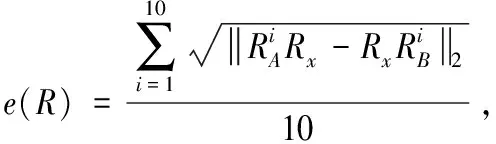
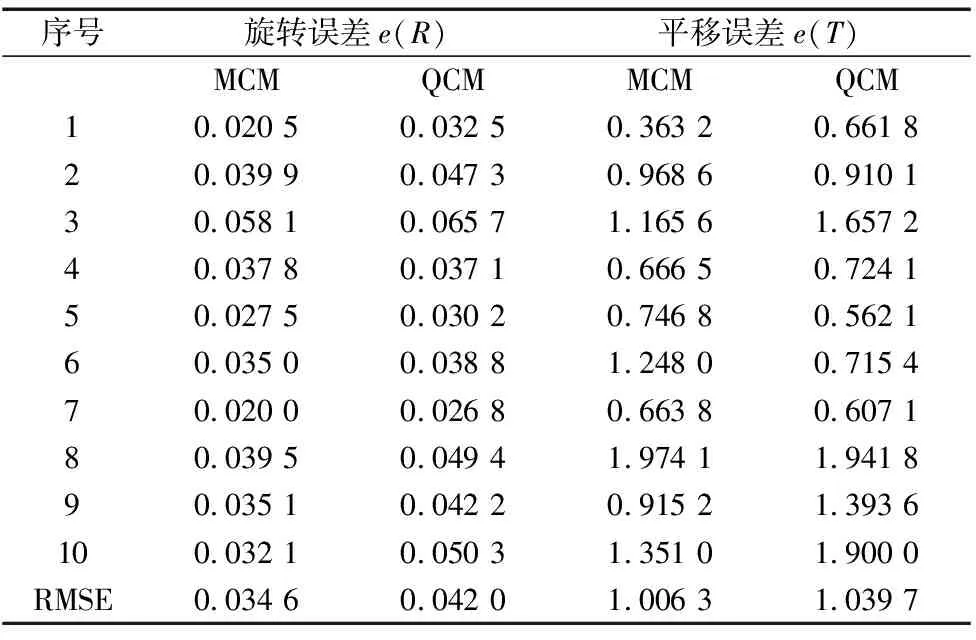
表1 验证实验结果

从表1可以看出，在10组重复实验中，本文所提手眼标定算法的精度可以满足机器人视觉系统在工件抓取应用中的需求，本文算法在旋转部分和平移部分的均方根误差相对传统算法分别减少了0.007 4和0.033 4。选取平移和旋转误差最小的一组求解值作为手眼标定矩阵的真实值，如下所示：

4 结论

本文基于四元数乘法可易性，结合最小奇异值筛选，提出了一种手眼标定方程解法，解决了基于四元数的和矩阵奇异值分解的手眼标定算法在标定时需要验证机器人末端执行器旋转角θ≠360°n(n=0,1,...)的问题。仿真实验的结果表明，本文所提算法对比传统算法具有更好的准确性和鲁棒性。验证实验的结果表明，本文算法在实际应用中具有可行性。