面向混流生产线排序问题的改进回溯搜索算法*

张天瑞，王译可，谢 薇，徐佳楠，王瑞麟

(1.沈阳大学机械工程学院，沈阳 110044；2.乌普萨拉大学土木与工业工程系，乌普萨拉 75261)

0 引言

多品种、小批量混流生产方式能快速响应市场需求[1]，但由于复杂的工艺和产品的多样性增加了生产系统的复杂性，导致混流生产线生产效率低下[2]。混流生产线高效生产过程中工件排序最为重要，计算过程的复杂性极高[3]。早期，学者们主要采用线性规划等方法求解，但由于其解决能力有限，仅能解决小规模排序问题[4]。近来，学者们以禁忌粒子群等智能算法对生产排序优化[5]， Tahriri F等[6]将遗传算法用于设置最小化混合模型装配线中的时间和成本；采用根据随蜂形式的精英保留策略，保证了一定的全局收敛能力[7]；刘琼等提出了一种改进的基于猫的行为模式线性混合比率的多个目标猫群体优化[8]；Zandieh M等[9]采用一种新的帝国主义竞争算法，确定最小完工时间和加工成本的混流生产排序问题；季树荣提出了一种基于混合蛙跳算法装配线排序研究[10]；刘冬等提出了一种改进粒子群算法[11]。

以上文献中，平衡和生产排序是混流生产的核心问题。在解决实际问题时，传统的优化方法面临解决求解时间过长的瓶颈，所以目前主流方向使用粒子群等启发式算法解决该类问题，但此类算法在求解过程中也存在收敛速度慢或全局搜索能力不足的局限性[12]。然而，回溯搜索算法因其较快的搜索速度和较强的全局搜索能力被广泛应用于各个领域[13-14]，但在混流生产平衡排序研究应用较少。综上所述，本文考虑组件消耗平衡，完成时间和产品切换调整时间构建以各个工作站的零件数使用率的最大化和总体的均准化为目标的函数模型，引入相应的系数，对模型进行加权求解；同时提出一种改进多目标回溯搜索算法，引入自适应变异尺度系数和数值扰动变领域搜索方法提高算法的收敛速度和搜索能力。

1 混流装配线排序问题描述与分析

企业在选择混装线投产顺序的优化目标时，应从实际出发进行有针对性考察，以免计算结果出现偏差[15]。目前主流投产排序目标包括：①保持各部件消耗率均衡；②单个工作站实现最少装配时间。本文以前者为排序目标。

本文假设已经解决混流装配线平衡问题，只分析产品的交付顺序，以达到各个工作站的零件数使用率的最大化和总体的均准化的目标。为了便于模型建立与分析，给定图1所示装配工序示意图。

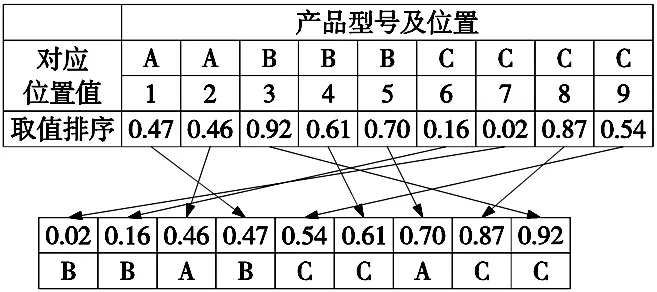
图1 产品相应映射位置示意图

2 问题模型构建

T表示每天生产的车型种类，Di为每天各车型的需求量，d表示每种车型的最大公因数，ri在一次生产中第i种车型生产的投产数量。

(1)

所以得到各个车型投产数量比为r1:r2:r3:…:rT，每T种车型的需求总数为：

(2)

在最小生产周期中，不同的型号要求在生产装置中使用组件j的总和为：

(3)

为了使各个零件j的消耗速度保持平衡，有必要在以前的k辆汽车生产中制定以前的调度计划，对零件j的实际需求量Vjk与理论上生产k辆汽车时零件j的需求量k·Q/R尽可能一致。使差异值最小化，定义操作差异值为：

(4)

车辆类型数量及零件清单如表1所示。

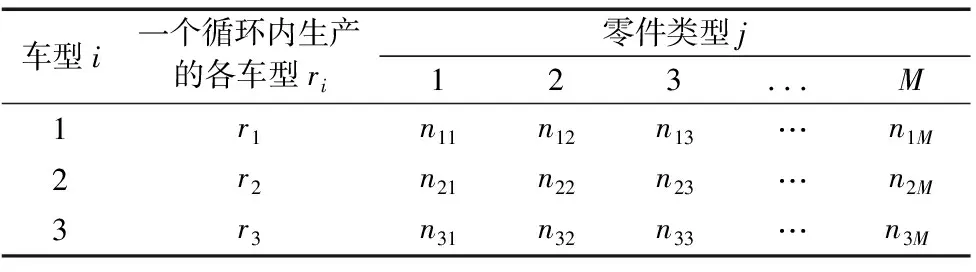
表1 车型数量及零件清单

续表

nij：表示在周期内，生产车型为i的车辆所需的组件j的数目；

Qj：表示装配全部车型一共需要组件j的数量，比如Q1表示在全部T种车型对零件1的需求总量；

ri：指一个最小单位中不同种车型的数目，其中i表示车型的类别，因此Qj用公式表示为：

Qj=n1j·r1+n2j·r2+…+nTj·rT

(5)

一个最小生产x循环中对零件j的理想用量为：

(6)

假设生产线上第一批k台车零件j的实际需求为Vjk，然后，可以表示为前k-1辆汽车对零件j的实际总需求量加上第k个车型i时对零件j的总需求量，用数学表达式表示为：

Vjk=Vj,k-1+Xik×nij

(7)

由上可得，该混合生产线前k辆汽车车型对零件j实际与理想使用量差值的二次方求和，目标函数如下式所示：

(8)

(9)

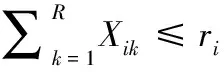
(10)

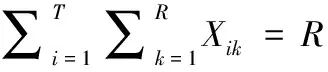
(11)

其中，式(9) 表示排序中，只能在前k个位置中的任何一个位置进行组装生产一辆汽车；式(10) 表示排序中，前k个位置对车型i的排序量不能大于最低单位巡回内i车型的总需求量；式(11) 表示在全部数量的汽车(共R辆)均参与到投产排序过程中。

3 改进的回溯搜索算法

回溯搜索算法(Backtracking Search Algorithm, BSA)，是一种基于种群的自然启发式算法，BSA的回溯功能保证了种群多样性和优越性，使其具有很强的全局搜索能力，但缺乏超前性，使算法后期局部挖掘能力减弱，影响收敛速度。此外，BSA变异大小系数设置范围波动过大，如果设置不当，会导致算法过早收敛，陷入局部解。为了解决BSA算法的局限性，将BSA算法进一步进行改进。

在变异步骤中，为提升迭代后期的局部搜索能力，有学者用历史种群中的最优个体进行引导[16]。在多目标优化问题中并没有绝对意义上的最优个体，故本文提出使用多权重下最优个体精英化历史种群，再用其引导当前种群进化的方法。目标函数选取最大完成时间l、总耗能m、平均完工时间n个权重值，可搭配出l×m×n种加权函数，在历史种群中寻找每种加权目标函数下的所有最优个体替换历史种群中其它个体，即可完成对历史种群的精英化，且保留了历史种群的多样性。

3.1 自适应变异尺度系数

在变异步骤过程中，选择较大的可控制变异程度系数F值，会导致种群形式增加，收敛速度持续降低；而选择较小的F值则相反。为了在早期的算法种群中保证形式多样性，同时对算法后期中的收敛速度保持增加，所以提出了自适应变尺度系数[17]。本文对其进行了简化，使F按公式(12)随迭代次数的增加而呈减小趋势，其中N(0，3)为服从(0，3)正态分布的随机数，n为迭代次数，C为常数。

F=N(0,3)×exp(-n/C)

(12)

3.2 变邻域搜索

本文提出一种数值扰动变邻域搜索方法，使算法在局部搜索中能力增强，并对算法交叉步骤中生成的试验种群V使用这两种方法进行变邻域搜索。

首先，对原序列上的实数编码加入数值扰动，使其产生与原解码结果相邻的解码结果。生成一个h×(1+m+w)×N的服从(0，3)正态分布的随机数矩阵R和一个(H-h)×N的零矩阵Z。将其合成为H×(1+m+w)×N的扰动矩阵D，则扰动后的种群Q*和原种群Q的关系为：

Q*=Q+D

(13)

其次，从工序排序、机器选择和工人指派问题上，随机从种群中选取个别个体，各随机选择两道工序，交换其在生产线上对应的编码，如图2所示。

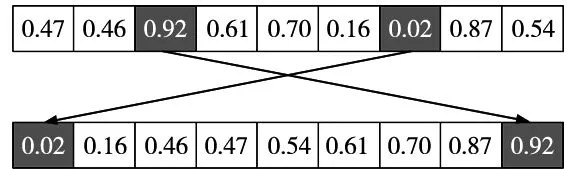
图2 混流生产线上交换工序位置编码示意图

3.3 按非支配等级更新当前种群

基于精英策略的非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm II，NSGAII)[18]采用快速非支配排序，选择一个非支配水平低的个体可以保证种群精英化。依据非支配等级确保优秀个体更新至当前种群。具体步骤如下：

步骤1：将种群P和种群V混合；

步骤2：将其中所有个体按其ID分组；

步骤3：对各ID进行快速非支配排序；

步骤4：按非支配等级从低到高逐层将各ID对应的个体更新至当前种群，待更新个体数小于当前所在支配等级数时，每从该层非支配等级的各ID中选出一个个体更新到当前种群，直到更新完成。

3.4 算法流程

改进多目标回溯搜索算法(Improved Muti-Objective Backtracking Search Algorithm，IMOBSA)的算法流程如图3所示。

4 混流装配线实例问题研究

4.1 某汽车公司混流装配线分析

B公司的整车混流装配生产线及其所在的生产系统均推行丰田生产方式满足个性化制造以及多车型共线生产的需求，且所有生产流水线生产类型、组织方式均一样。

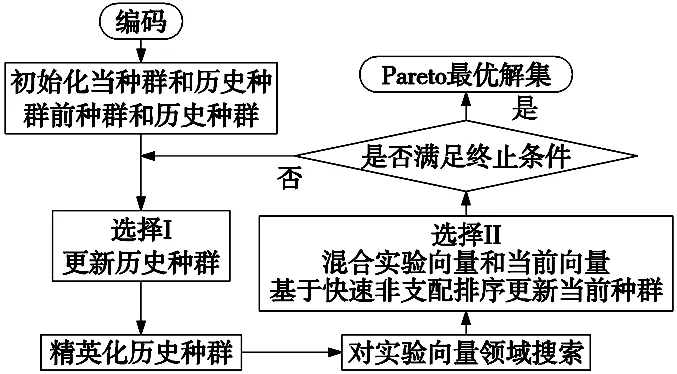
图3 IMOBSA流程图

该公司现有3系标准轴版轿车和长轴版轿车与5系标准轴版轿车和长轴版轿车在装配线上混流生产组装，在本文中将这三种类型的汽车编号为A、B、C、D，现己明确在一个生产周期内要生产装配出A型车4台，B型车3台，C型车2台以及D型车3台，(即A：B：C：D=4：3：2：3)，如表2表示某天某批次生产计划。

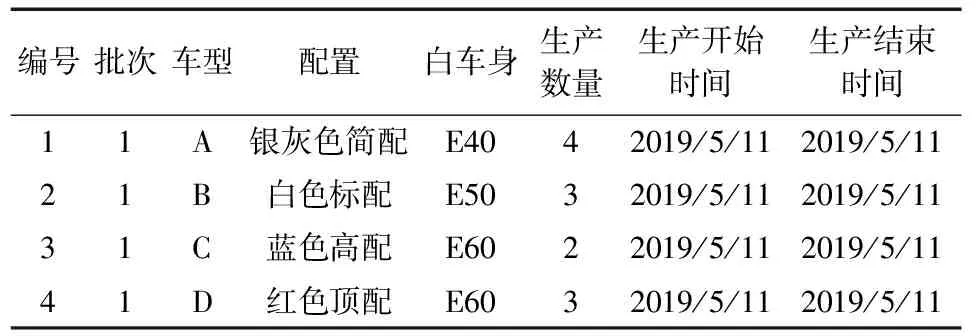
表2 某天某批次生产计划

给定两个方案：12辆汽车在总装线上需要的主要结构部件有5种，同时安排5个工作站进行装配生产，每个作业站仅对应一种零件；12辆汽车在5个作业站上依次进行装配工作。在一个最小生产周期内，5种主要构件的总需求量分别为：74、74、73、54、52，每当需要某个零件时，5种主要零部件能够准时送达各个工作站的零件缓存区。

模型假设：

(1) 这两种方案都确保各方同时组装的汽车数量相等；

(2) 每个作业站上安装不同种类的汽车的时间都相同；

(3) 不会出现作业超时的情况。即在各个工作站里每个组件都能够在计划的时间点里安装完成。

B公司对该系列4种车型进行总装，每种车型所必须的种类元件的数量如表3所示。

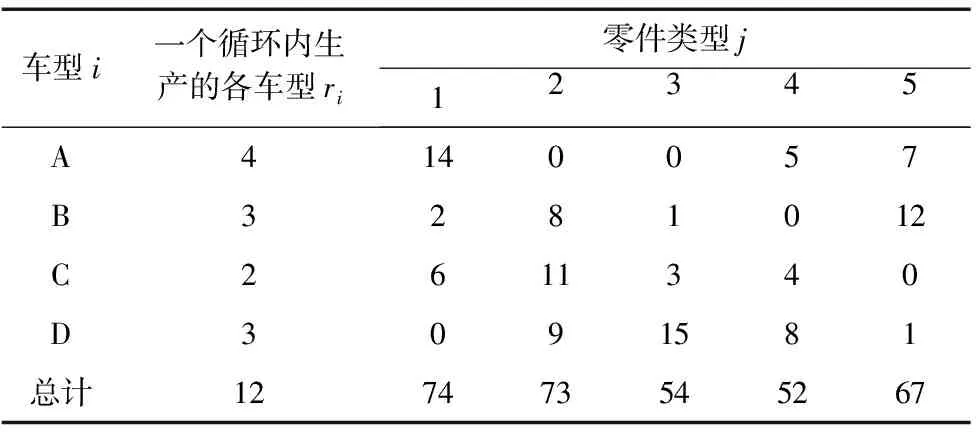
表3 种类元件的数目

4.2 IMOBSA的排序方案

根据目标函数(8)可知，目标函数越小表示排序方案越合理。根据约束函数，编码方案为[ 1 1 1 1 2 2 2 3 3 4 4 4 ]。在一个最小生产循环中，全部产品A(i=1 , . . . ,T)的总产量为：

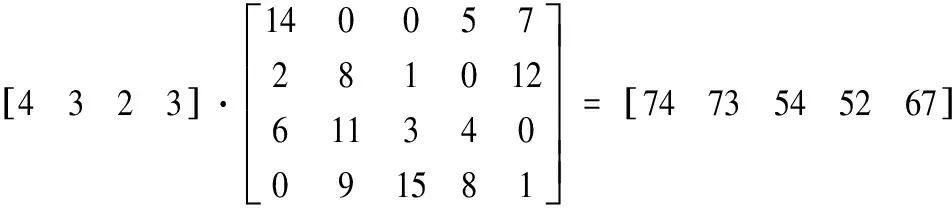
求得dj：

将数据带入回溯搜索算法求得，当k=1，i=3时Dij值最小，即首先将C车型在这个最小生产循环内进行投产排序。表4表现了最小生产循环内各个目标值。

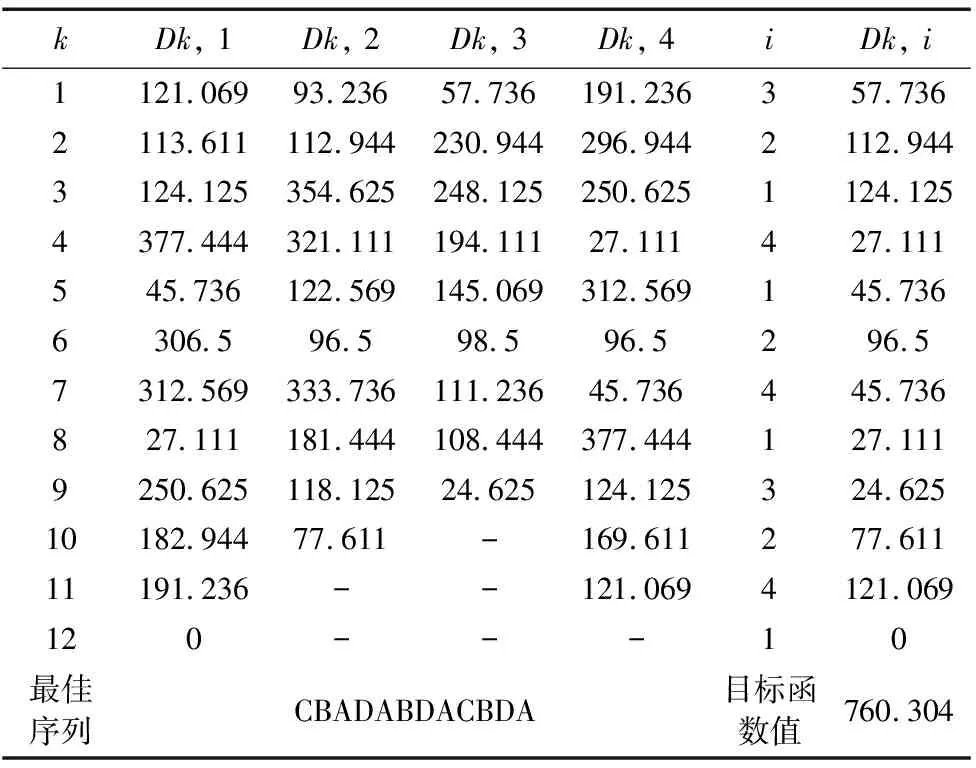
表4 最小生产循环内各个目标值

5 算法验证

本文根据 Python 2.7 编程进行建模，所使用计算机的处理器型号为Intel(R)Core(TM) i5-5200U CPU 2.2 GHz，内存8.0 GB。为了与其他算法在同一水平上进行比较，本文的大部分主要参数都与传统的遗传算法中的部分参数一致。算法参数具体设置：种群个数设置为10，交叉概率Pc=0.8，变异概率Pm=0.1，其中历史种群、父代种群、实验种群的个数相等，最大迭代次数设置为5000。如下结果分别为IMOBSA、BSA和GA，算法计算10次并进行比较的适应度值结果如图4所示。

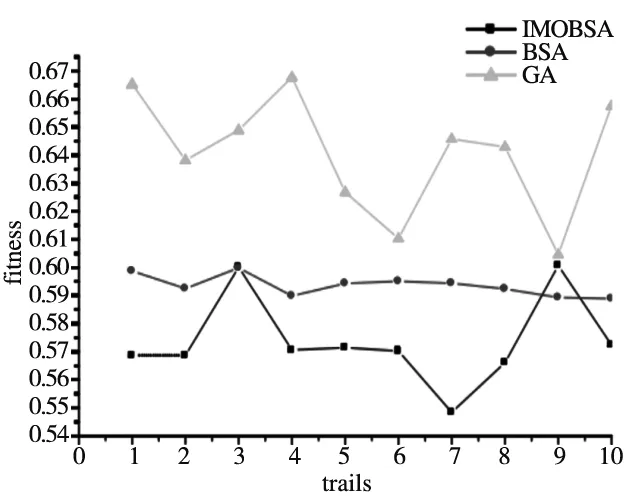
图4 IBSA、BSA、GA 算法运行10次的适应度值结果

由图4可知，在解决装配线问题上，BSA和IMOBSA算法的收敛效果比GA算法的好，而IMOBSA算法运行10次的结果大部分都比BSA算法的要好，证明了改进后的BSA算法具有更好的收敛效果。IMOBSA算法第7次的运算结果是最好的，BSA算法的第10次运算结果是最好的，GA算法的第 9 次运算结果最好。

根据3种算法计算所得的最优解适应度值收敛曲线如图5所示，由图可知，GA算法在图中显示虽然具有很快的收敛速度，但是最优适应度值不理想。而改进后的IMOBSA算法比未改进的BSA算法更有优势且效果更好，既避免了算法的早熟收敛，也提高了收敛速度。

图5 三种算法的最优解适应度值的收敛曲线

6 结论

本文针对复杂产品混流生产线生产效率低下的问题，考虑组件消耗平衡、完成时间和产品切换的调整时间等因素，以各个工作站的零件数使用率的最大化和总体的均准化为优化目标，对某汽车制造企业的混流生产线排序进行优化。

(1) 针对BSA存在随机性强导致算法后期局部挖掘能力变弱，以及变异尺寸系数设置范围波动过大的特点，应用自适应变尺度系数和数值扰动变领域搜索方法对BSA进行了改进，设计了IMOBSA算法流程，提高了算法的搜索能力。

(2) 将改进多目标回溯搜索算法用于某混流装配线的作业排序问题，得到了较好的排产结果，可为混流生产线排序提供参考依据。

(3) 采用Python 2.7编程，将改进算法与回溯搜索算法、遗传算法生成的排产方案进行比较，结果表明，改进算法效率更高，早熟收敛程度低，收敛速度快。