非刚体点匹配问题中点对应关系的分析

上官晋太，连玮

（长治学院 计算机系，山西 长治 046011）

0 引言

点匹配方法是非刚体图像配准中的一个最基本的方法，广泛地应用于计算机视觉、图像分析和模式识别的过程中［1-6］。比如，图像融合［7］就是典型的点匹配问题。与其他基于特征的匹配方法相比，点匹配方法更加简单，且点匹配方法也是其他基于特征的匹配方法的基础，因此，其在非刚体图像配准中受到了越来越多的重视。非刚体点匹配涉及两个基本的过程，第一个是两个点集中点与点的对应关系的确定，第二个是点集之间的非刚体变换。这两个问题不是互相独立的，它们之间相互影响，一旦其中之一被确定了，对另一个的求解就是非常简单的事情。对于点匹配问题的解决，一般有两种途径，一种是将对应关系和空间变换分别处理，只解决其中之一，另一种是将两个问题联合处理，我们可以将点之间的对应关系和空间变换看成是两个变量，用迭代的方法先保持一个变量不变，估计另一个变量，然后在得到估计量的基础上，保持这个估计量不变，对先前不变的那个变量进行新的估计，在交替的过程中两个变量相互改进，直到得到最终的优化解。因此，我们可以将第一种途径称之为独立估计法，第二种称之为联合估计法。到目前为止，在已发表的文献中大部分只专注于解决刚体变换问题，比如，已提出的惯性矩法［8］，此法先求出数据的“质心”和“主轴”，“质心”可以用来解决空间变换中的位移问题，而“主轴”提供数据集的整体的指向，由此可以解决数据集的旋转角度问题。同样，只用于解决刚体变换问题的方法还有Hough 变换［9］，Hausdauff 距离［10］等，这一类的方法属于独立估计法。现实生活中，非刚体配准的应用场合更广泛一些，比如医学图像配准就是典型的非刚体图像配准［11-12］。非刚体的配准，由于最优解的搜索空间维度过大，求解过程过于复杂，所以一般利用联合估计法。在联合估计法中，两个点集之间对应关系的确定是解决问题的关键所在。常用的方法有形状上下文方法和基于迭代最近点的方法。

形状上下文算法是通过一个基于轮廓的形状描述子，来表达点集中一个点和其余点的相对位置关系，点与点的对应关系通过最小化形状上下文距离之和来实现。在利用形状上下文进行非刚体点匹配时，贾耕云等［13］提出了一种具有对称不变性的改进形状上下文特征提取与匹配的算法，该算法能够有效地在互相对称的相似图像间建立匹配，从而使匹配更加稳定。师硕等［14］针对人脸匹配在光照、姿态、表情等背景因素影响下匹配准确率低的问题，提出了一种基于SURF 和形状上下文的人脸匹配算法，此方法的应用有效地增加了匹配点对数目，提高了人脸图像匹配的准确率。化春键等［15］提出的改进算法，引入双局部二进制模式纹理特征权重值，利用梯度信息使得该算法对噪声、光照变化具有较高的鲁棒性。这些方法均对形状上下文匹配算法进行了一定程度的改进，但都未解决传统算法容易产生点对之间的误匹配问题，特别是当采样点在栅格交界处，即在相邻两个栅格边界位置时，在有轻微形变的情况下，就会引起阶跃变化，从而导致误匹配。

另一种常用的点匹配的算法是迭代最近点算法（Iterative Closest Point，ICP）［16］，此算法通过在两个点集间进行双向的最近点确认，得到对应矩阵，由对应矩阵得到模板点集到目标点集的映射位置，从而建立点对应关系。石爱军等［17］提出了遗传算法结合自适应阈值约束的ICP 算法，此算法可以提高配准精度，同时减小配准时间，能在一定程度上满足实时性的要求。张春雷等［18］提出了一种将三点法与迭代最近点算法结合的配准策略，其配准精度和稳定性均优于传统算法，且具备高效、易于操作的特点。以上这些改进的迭代最近点算法在性能上都有一些提高，但是均无法解决迭代最近点算法易于收敛于局部最小值点的缺点。本文针对这一个问题，提出了在对应矩阵上加适当随机扰动的方法，来产生更加合理的点对应关系，从而可以避免非刚体点匹配过早地陷入局部最小值点。

1 两个点集中点对应关系的确定

在联合估计法中，有一种方法最为常见，那就是基于ICP 的联合估计法。它的原理就是先在两个点集之间初步确定对应关系，在对应关系确定后进行空间变换，空间变换后可得到新的估计点集，用此点集与目标点集再一次进行对应关系的确定，这样周而复始地进行对应关系和空间变换的轮流迭代，最后收敛于一个全局最优点。图1 是要配准的两个点集，分别为模板点集Q 和目标点集P［3］。配准的任务是将模板点集经过空间变换匹配到目标点集上去。

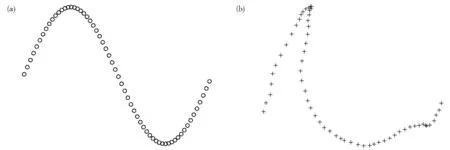
图1 （a）模板点集Q 和（b）目标点集PFig. 1 （a）Template point set Q and（b）Target point set P

首先，对模板点集中的每一个点，在目标点集中找到离自己最近的点，这样可以形成一个模板点集到目标点集的对应矩阵M1，矩阵中的行号为模板点集中对应点的标号，矩阵中的列号 为 目 标 点 集 中 对 应 点 的 标 号 ，若M1(i，j)=1，说明模板点集中的第i点在目标点集中找到的最近点为第j个点。再对目标点集中的每个点，寻找在模板点集中的最近点，形成目标点集到模板点集的对应矩阵M2，M2中的行号和列号规定和M1中是相同的。将两者进行平均得到两个点集之间的双向对应矩阵M。 有M=0.5(M1+M2)。 为 了 观 察 和 叙 述方便，对图1 中的两个点集分别进行等间隔抽样，得到两个均由8 个点形成的点集来说明双向对应矩阵M的形成过程。抽样后形成的点集如图2 所示。用ICP 法可以得到模板点集到目 标 点 集 的 对 应 矩 阵M1，其 中，除M1(1，5)、M1(2，4)、M1(3，3)、M1(4，7)、M1(5，8)、M1(6，8)、M1(7，8)和M1(8，8)为1 外 其 余 都 为0，说明模板点集中的第1 个点在目标点集中找到的与自己最近的点为第5 点，以此类推，模板点集中的第8 点在目标点集中找到的与自己最近的点也为第8 点。在这里可以看到，两个点集之间并非一一对应关系，模板点集中的5、6、7、8 这4 个点在目标点集中的最近点都是第8点。这样的多对一，或一对多的关系是非刚体点匹配中比较难解决的问题之一，这也会造成匹配困难。同样的方法，求目标点集到模板点集 的 对 应 矩 阵M2，可 知，M2矩 阵 中 除M2(1，1)、M2(1，5)、M2(2，2)、M2(2，3)、M2(2，4)、M2(5，6)、M2(5，7) 和M2(5，8) 为1 外 其 余 都 为0，说明目标点集中的第1、5 点在模板点集中找到的与自己最近的点都为第1 点。目标点集中的2、3、4 点在模板点集中找到的最近的点都是第2 点。目标点集中的6、7、8 点在模板点集中找到的最近点都是第5 点。从图2（b）中可以看到两个点集中的对应关系。由此形成的双向对应矩阵M，再对M按行进行归一化处理可得M′，结果如下所示：

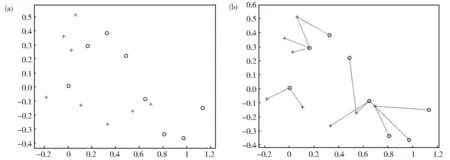
图2 抽样后两个点集形成的对应关系（a）抽样后的两个点集；（b）两个点集之间的点对应关系Fig. 2 Correspondence between two sampled point sets（a）Two sampled point sets；（b）The correspondence between two point sets

由归一化后的双向对应矩阵M′，可以求出变换后的新的点集Q′。变换公式如下：

如果直接利用M′矩阵进行计算，所得到的点将会出现归并现象，点数将会减少，这样就无法在两个点集之间建立起一一对应的关系，匹配的结果很可能会陷入局部极小值，无法得到全局最优解。通过观察矩阵M′可以找出产生点归并现象的原因，在此矩阵中M′(6，8) 、M′(7，8)和M′(8，8)都为1，这使得通过公式（1）产生的映射会出现3 点并1 点的结果。为了避免这样的情况发生，可以在矩阵M上加上一个随机扰动。图3 为不加扰动与加扰动的对比情况。

从图3 的（a）中可以看到，如果在对应矩阵M上不加扰动，利用归一化后的矩阵M′进行变换，得到的新点集Q′只有6 个点，用这6 个点与目标点集的8个点进行匹配是不合理的。在图3 的（b）中加上了随机扰动，这样可以恢复到8 个对应点的状态。这样做有利于匹配结果收敛于全局最优点。

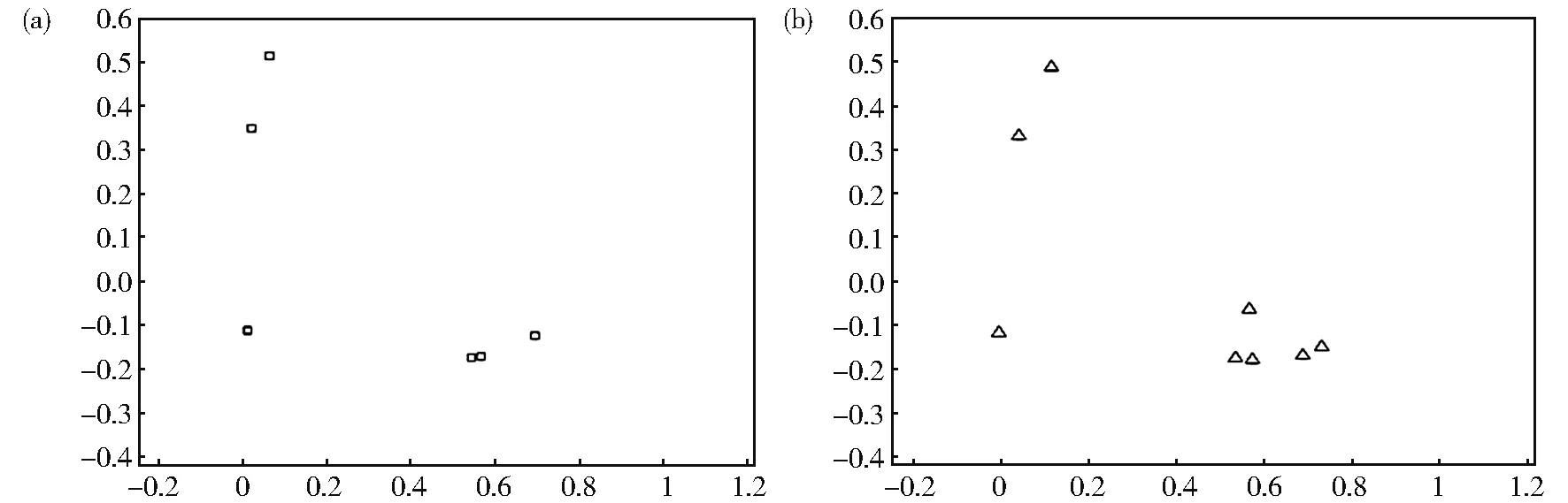
图3 对应矩阵M 加随机扰动与不加扰动情况对比（a）没有加随机扰动的情况；（b）加随机扰动的情况Fig. 3 Comparison between the situation with and without random perturbations on the corresponding matrix M（a）The case without perturbation；（b）The case with perturbation

2 空间变换

非刚体匹配中，最常用的空间变换是薄板样条插值法。此方法源自数据插值和函数逼近理论［19］，它寻找一个通过所有的控制点的弯曲最小的光滑曲面。设：

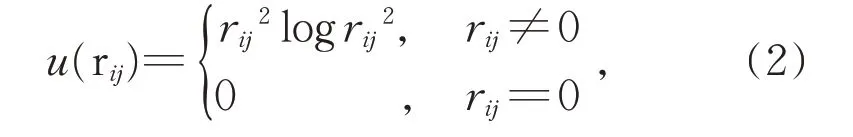
其中rij=|pi－pj|代表两点之间的距离。再定义如下矩阵：

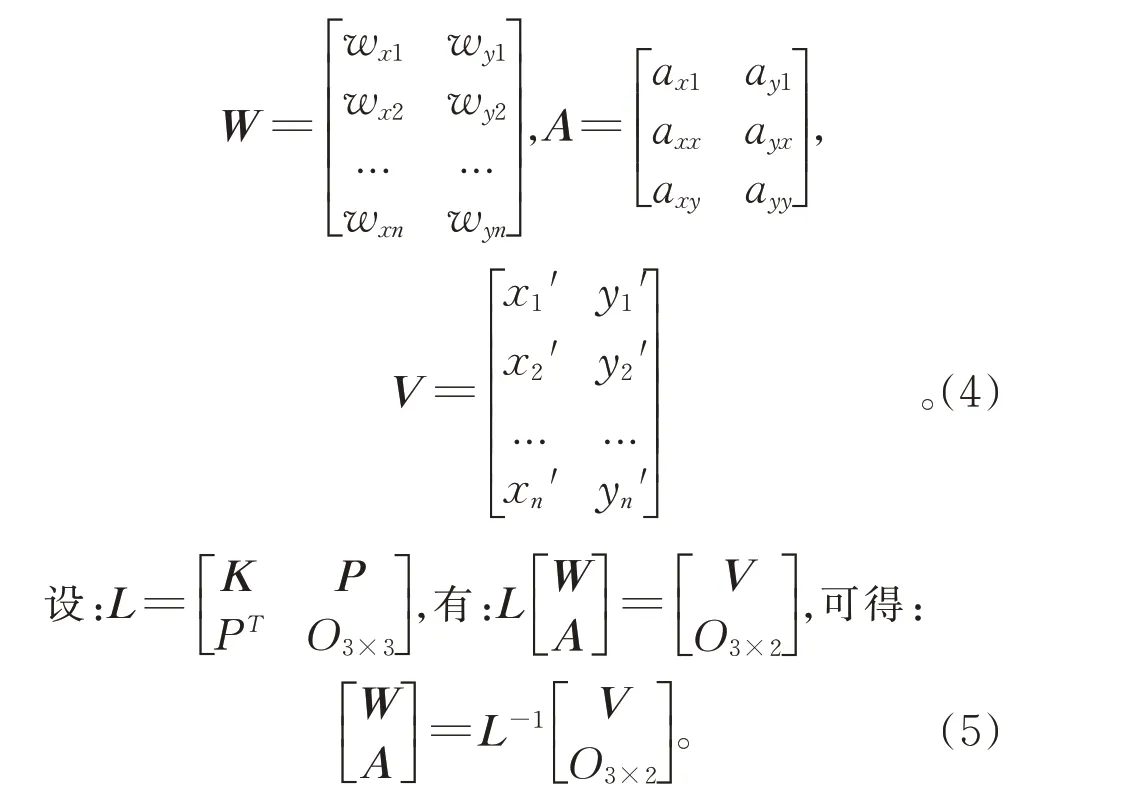
求得w和a后，已知点坐标(x，y)可求得变换后的坐标(x′，y′)，二者之间关系为：

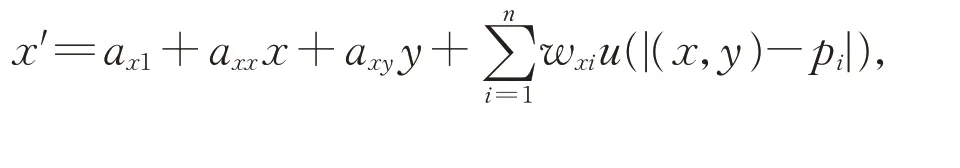
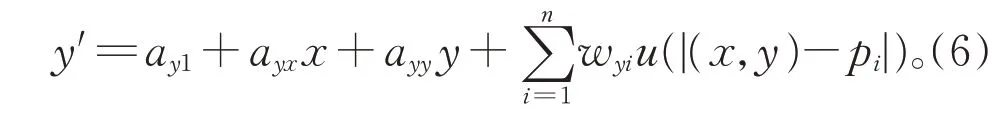
3 配准实验及结果

用图1 中的两个点集进行匹配实验，对应关系矩阵的求解和空间变换交替进行，每一步的迭代都是向最终解的逼近，经过多次的运算，最后得到一个全局最优解。图4 是匹配过程及结果，在图（a）中可以看到两个点集之间的对应关系，在目标点集曲率大的地方，出现了多对一或者一对多的情况。图（b）是最终匹配结果，除曲线的顶点处和末尾处外，其余部分都得到了较好的配准。图（c）是空间变换情况，显示了原点集的网格图（虚线部分）和变换后的网格图（实线部分）之间的对应关系。

图4 匹配实验与结果（a）点集之间的对应关系；（b）配准结果；（c）空间变换Fig.4 Registration test and result（a）Correspondence；（b）Registration result；（c）Transformation

不同的随机扰动会对最后匹配结果产生不同的影响。图5 是在双向对应矩阵M上加不同程度随机扰动后的匹配结果。可以看到：图（a）为没有加随机扰动的情况，模板点集的点普遍下移，造成两个点集在顶点部分没有得到很好的配准，图（b）是在双向对应矩阵M上加0.26 倍的均值为0、方差为1的正态分布的随机扰动时的情况，在整个范围内，模板点集和目标点集得到了比较好的匹配。当所加的随机扰动进一步增大到0.6 倍时，匹配结果如图（c）所示，此时的匹配结果，甚至比不加随机扰动时还要差，这是因为过量的随机扰动，造成了对应关系的模糊，由这种模糊引起的对应的不确定性会引起匹配效果的恶变。

图5 不同程度随机扰动的匹配结果对比（a）无随机扰动；（b）随机扰动系数为0.26；（c）随机扰动系数为0.6Fig.5 Comparison of registration results with different degree of perturbation（a）Without any perturbation；（b）The perturbation coefficient is 0.26；（c）The perturbation coefficient is 0.6

为了定量地研究在对应矩阵上加不同程度的随机扰动对匹配结果的影响，本文中先定义配准误差如下：

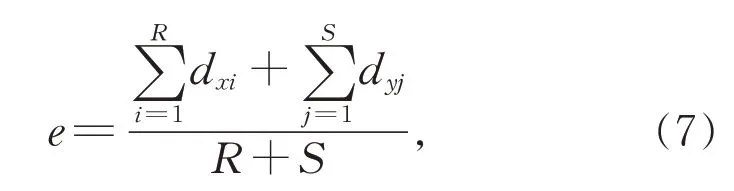
其中，dxi为变形后的模板点集Q′中的每个点与其在目标点集P中找到的最近点之间的距离，dyj为目标点集P中的每个点与其在模板点集Q′中找到的最近点之间的距离。R和S分别为模板点集和目标点集的点数。我们以步长为0.1，范围从0 到1 取11 个值，作为加在对应矩阵M上的均值为0、方差为1 的正态分布随机扰动的系数，每一种情况下运行30次，最后计算配准误差的均值和方差，结果如表1所示。

由表中数据可知，当没有在对应矩阵M上加随机扰动时（此时扰动系数为0），配准的结果是固定不变的，每次配准的误差都为0.019 3，此时方差自然为0。对于随机扰动系数不为0 的情况，其配准结果是一个概率分布问题，从表1 中可以看出，配准误差的均值最小值点在0.2 到0.3 之间，当随机扰动系数大于0.5 以后，配准误差急剧增加，这是因为过大的随机扰动掩盖了点之间对应关系的本质特性。为了进一步找到最小值点的位置，再取步长为0.01，范围从0.21 到0.3 取10 个值，作为随机扰动的系数，每一种情况下同样运行30 次，最后计算配准误差的均值和方差，结果如表2 所示。从表中可以看到，当所加正态分布的随机扰动系数为0.26时，配准误差的均值最小为0.014 4，说明此时的配准效果最好，其结果也好于没有加随机扰动的情况。

表1 扰动系数从0到1，步长为0.1时配准误差的情况Table 1 The registration error when the perturbation coefficient ranges from 0 to 1 and the step size is 0.1

表2 扰动系数从0.21到0.3，步长为0.01时配准误差的情况Table 2 Registration error when the perturbation coefficient ranges from 0.21 to 0.3 and the step size is 0.01

为了讨论此方法对不同数据图集的适用性，本文选择不同的点集进行配准实验，图6 是本文用于配准实验的点集，分别为点集1 到点集8。图中用“○”和“+”分别代表模板点集和目标点集。

图6 用于配准实验的点集Fig. 6 Point sets used for registration experiments

和前面一样，采取由粗到细的方法，先以步长为0.1，从0 到1 选取随机扰动系数，每一种情况下运行30 次，最后观察其配准误差的均值和方差，在可能最小值点附近，再以步长为0.01 取10 个值，作为随机扰动系数进行进一步配准实验，以配准误差最小为原则，兼顾考虑方差影响，找到对于此点集的最优随机扰动系数。对于不同的点集其结果如表3 所示。从表中可以看到，对于不同的点集最“合适”的扰动系数并不相同，这与点集组成的复杂程度、模板点集和目标点集之间的相对位置及二者之间的形变有关。

表3 不同点集的配准实验结果Table 3 Registration experiment results of different sets

为了和没有加随机扰动时的情况进行比较，表4 中列出了图6 中的8 个点集，在随机扰动系数为0时的配准误差。对比表3 和表4 可以看出，同序号的点集在其对应矩阵上加上合理的随机扰动，其配准误差小于无随机扰动时的配准误差。表中同时列出了二者之比，这些比值的均值为0.551 6，即加上适当的随机扰动后，配准误差可以减小到原来的一半左右。这说明一般情况下，此算法对不同点集的配准精度会有一定程度的提升效果。

表4 扰动系数为0时不同点集的配准实验结果Table 4 Registration experiment results of different sets when the perturbation coefficient is 0

4 结论

在联合估计法的非刚体点匹配过程中，我们应用了对应关系和空间变换交替迭代的方法来完成整个配准过程。对应关系和空间变换在这个迭代过程中相互改进，目的是使最终的配准结果能收敛于一个全局最优点。在这个过程中，我们首先确定对应关系，对应关系的确定是下一步空间变换的基础。由于两个点集的点与点之间关系的复杂性会导致对应关系中多对一或者一对多的情况出现，这就为下一步空间变换带来了一定的难度。如果不进行适当的干预，最终的配准会导致得到的是一个局部最小值点。我们的办法是在得到的对应矩阵M上加上一个适当的随机扰动，然后再对矩阵M按行进行归一化处理，得到矩阵M′，这样得到的变换后的点集与目标点集进行配准可以得到更好的结果。本文对多组已知点集加不同程度的随机扰动，通过多轮仿真实验，结果表明此方法有效。