PEMFC分区电流测量的关键影响因素分析*
刘旭东,魏学哲,陶建建
(同济大学新能源汽车工程中心,上海201804)
前言
质子交换膜燃料电池(PEMFC)一般具有较大的电化学反应有效面积,尤其是在车载应用下。建立多维机理模型以分析PEMFC内部的电流密度、反应气体和水含量等参数分布的不一致性,其仿真结果需要与可靠的分区测量实验数据进行比较,以验证模型,从而为PEMFC设计与控制的优化提供依据。其中,针对电流密度,近年来有不少研究采用各种方式以测量PEMFC主平面内的二维电流密度分布。该测量需要解决两个基本问题:一是分区集流,即对膜电极(MEA)和双极板等部件中的哪一些进行分区,之后通过怎样的集流体将各分区电流引至电流传感器;二是电流检测,即采用何种原理转换电流信号,常用的有欧姆定律、霍尔原理和软磁体的磁化等。
Weng等[1]将MEA、双极板和集流板等部件均分为8个独立的分区,各分区电流分别引至外部,事实上形成了多个子电池,各子电池可单独连接电子负载并测量电流。Liang等[2]仅对集流体和端板进行分区,分区电流引至外部后通过15个LEM LT58⁃S7霍尔元件,利用霍尔原理测量电流。Peng等[3]设计的多层印制电路板(PCB)的两面分别由镀金焊盘与PEMFC部件接触以集流,电流被焊盘上的一组过孔引至PCB中间层埋入安装的分流电阻,再通过另外一组过孔引入PCB反面,类似的集成测量元件的PCB设计也被其他研究采用[4-7]。基于PCB的设计无须或仅对双极板进行分区,改动小,应用方便,是现阶段常用的分区电流密度测量方式。然而,由于不分区的部件存在绝缘性问题,因此侧向电流带来的分区串扰问题难以避免,这将降低测量精度。Ghosh等[8]指出石墨双极板更高的平面内电导率带来的侧向电流将使电流密度分布均匀化。Eckl等[9]针对气体扩散层(GDL)和双极板建模,分析双极板是否分区及分流电阻阻值对于测量精度的影响。Schulze等[10]认为在其实验条件下,GDL和双极板中侧向电流带来的分区电流串扰在相邻分区电流差异的10%左右。
本文中针对基于PCB和分流电阻的分区电流密度测量装置,参考一种PEMFC结构,在COMSOL Multiphysics中建立并简化两种PCB方案、双极板和GDL的几何模型,通过有限元数值仿真以分析不同的设计和装配参数对侧向电流和分区电流密度测量精度的影响程度,包括装配压力、电阻安装方式、分区数量、双极板电导率和温漂,并提出相应的设计和优化方向。
1 模型建立
本文中在给出PCB电流测量方案和建模时参考的PEMFC具有较为常见的结构,从中间的MEA起向两侧依次为石墨双极板、铜制集流板和端板,MEA有效区域为50 mm×50 mm,整个PEMFC使用4对螺栓螺母进行紧固和定位,紧固力矩利用扭矩扳手施加,以获得实验所需的接触应力。
1.1 PCB模型
考虑到原有石墨双极板的比热容及与GDL的接触特性,为尽可能减少插入PCB对电化学反应的影响,本文中选择将PCB插入双极板与集流板之间,而不取代任何原有部件。下文中给出电阻表面贴装和埋入安装两种安装方式的PCB设计及模型。
1.1.1 表面贴装方案
由于贴装在PCB表面的电阻具有一定厚度,为保证PCB与双极板和集流板的可靠接触,电阻的贴装位置必须布置在它们的接触区域以外,对于本文参考的正方形MEA,这将限制分区数量的增加,否则MEA中间部分的分区电流难以从PCB中间层传导至贴装区域,因为压缩导线宽度将使压降过大而显著降低PEMFC输出性能。考虑25 cm2的MEA有效 面 积,选 择3×3、4×4和5×5 3种 分 区 数 量,在Altium Designer中绘制PCB,正面布置相应数量且相互绝缘的集流焊盘与双极板接触,每个焊盘上布置一组的过孔与中间层导通,电流从中间两层导线传导至接触区域以外,再通过一组过孔导通至贴装在PCB反面的电阻,流经电阻后汇聚到反面的镀金大焊盘,与集流板接触。以4×4分区为例,PCB布线如图1所示。
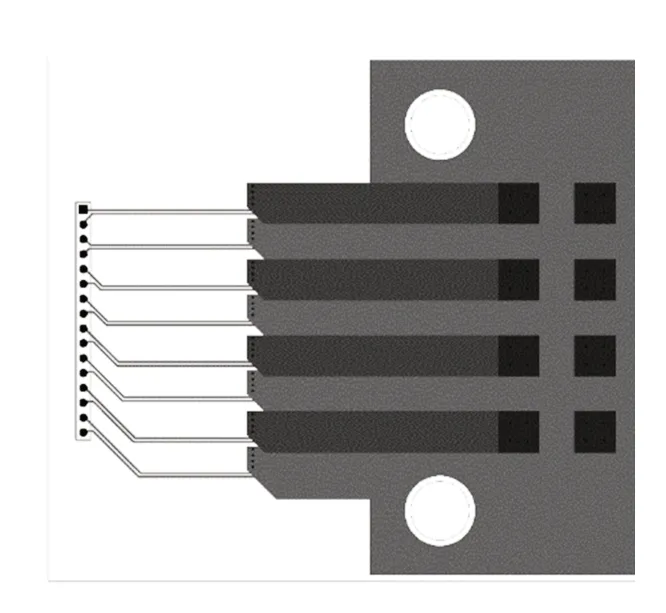
图1 表面贴装电阻的PCB布线
1.1.2 埋入安装方案
埋入安装的电阻可直接布置在对应的正面集流焊盘之下的PCB中间层,无须用导线引出至接触区域以外,但考虑到每个分区需要布置两组过孔,且电阻元件也占据一定面积,故分区数量也不能过多。为方便对比分析,选择与表面贴装设计相同的3种分区数量,电阻和过孔的布置参考Geske等[11]给出的布线图,如图2所示,其他部分与表面贴装一致。
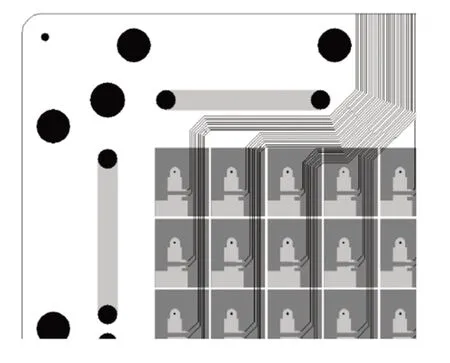
图2 Geske等[11]设计的埋入电阻PCB布线
1.1.3 PCB几何模型
上述两种PCB方案具有对称性,且不同分区的电路总电阻可以通过优化线宽和线形等设计达到基本一致,所以仅对一个分区的电路进行建模以减少计算量。同时,电阻元件按照电阻的标称值简化为在电流方向上具有相等直流电阻的长方体,不考虑阻值制造误差、温漂和焊锡以及元件外形的影响。埋入安装电阻电路的模型简化方式与表面贴装基本一致,仅在中间层导线长度、过孔布置和电阻等效长方体的位置等方面有所不同。在COMSOL Multiphysics中建立两种电阻安装方式的PCB电路几何模型,设电阻阻值为R,表面贴装模型如图3所所示,电路总电阻为Rf;埋入安装模型如图4所示,电路总电阻为Re。
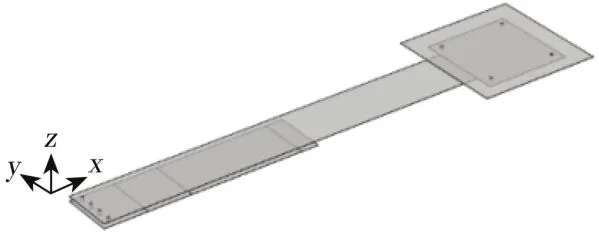
图3 电阻表面贴装PCB电路几何模型
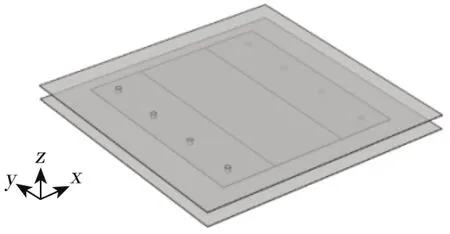
图4 电阻埋入安装PCB电路几何模型
1.2 电池部件模型
本文中主要研究侧向电流对于测量精度的影响,因此考虑到仿真复杂程度,暂不对电化学反应过程进行建模,而是直接对模型施加一定的电流边界条件。尽管反应电流在三相区产生,需要经过催化剂层(CL)、GDL和双极板才能被PCB的集流焊盘收集,但考虑到CL的厚度仅为GDL的几分之一甚至更小,GDL的厚度又与双极板不在一个数量级,因此考虑大致的侧向电流大小和仿真计算量,仅对GDL和双极板进行建模,电流边界条件直接施加在GDL一侧的表面上。
1.2.1 双极板
Eckl等[9]指出若按照原样对流道进行建模,则网格划分和数值求解的计算量可能较大,因此他们采用体积数值平均法(NVAM)进行简化,将双极板流场部分划分为具有重复性的基本体积单元,求解单元的三向等效电导率,从而建立表面平整的双极板等效模型。然而,蛇形流场必然存在几组x方向的流道,双极板进行NVAM简化后仍不能认为是均匀电导率,且不能反映双极板与GDL的实际接触情况,因此本文中按照流场原结构进行建模,模型如图5所示,模型参数见表1,表中以符号表示的参数将在下文中赋值。

图5 双极板几何模型
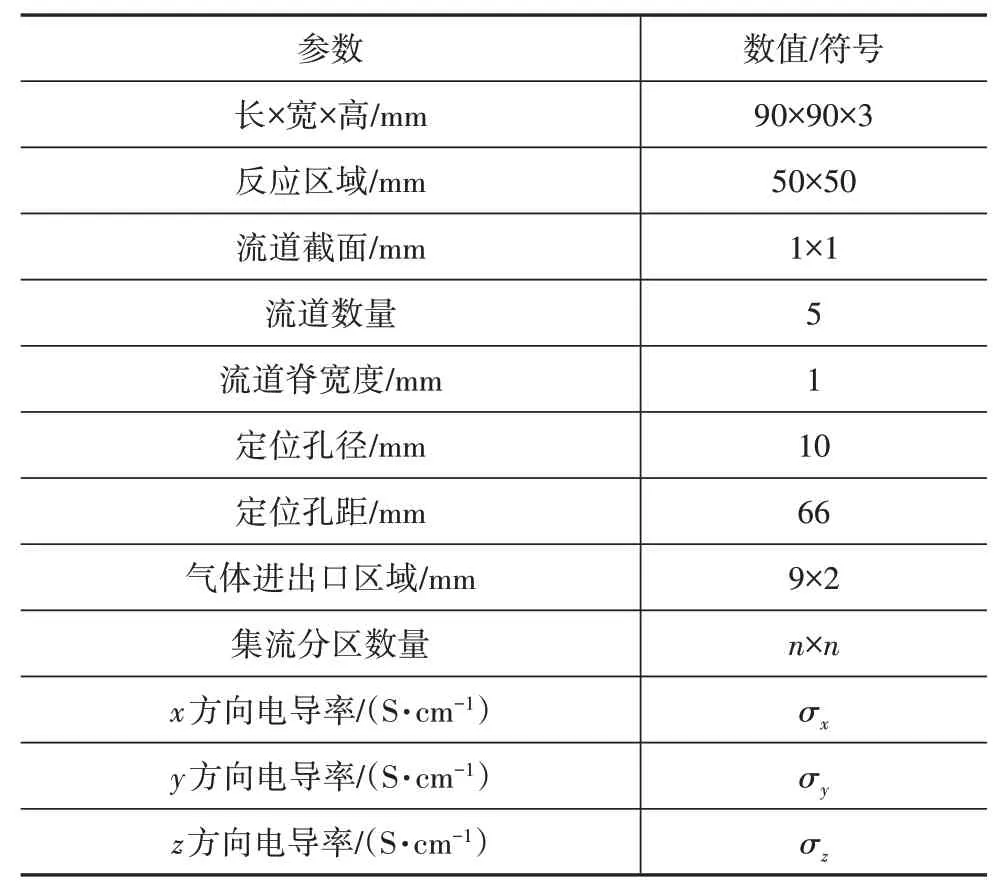
表1 双极板几何模型的参数
1.2.2 GDL
本文中参考GDL⁃10BB型号进行建模。对于厚度,GDL主要与流道脊接触并受其压力,并非均匀压缩,也不具有均一厚度,而GDL剩余部分虽未受到直接压缩,但仍会产生一定的形变,这种不均匀压缩特性的描述较为复杂[12]。考虑到GDL较小的厚度,且将求解不同压力下的侧向电流情况,为了降低仿真计算量,假设GDL压缩后为均匀厚度进行建模。对于电导率,Freunberger等[12]指出,GDL受不同压力压缩后在x、y方向上电导率变化较小,因此x、y方向的电导率参考Eckl等[9]给出的数据,并假设不随压力变化而改变,z方向电导率则参考Mishra等[13]给出的电导率-压力特性曲线进行计算。GDL模型如图6所示,模型参数见表2。
图6 GDL几何模型
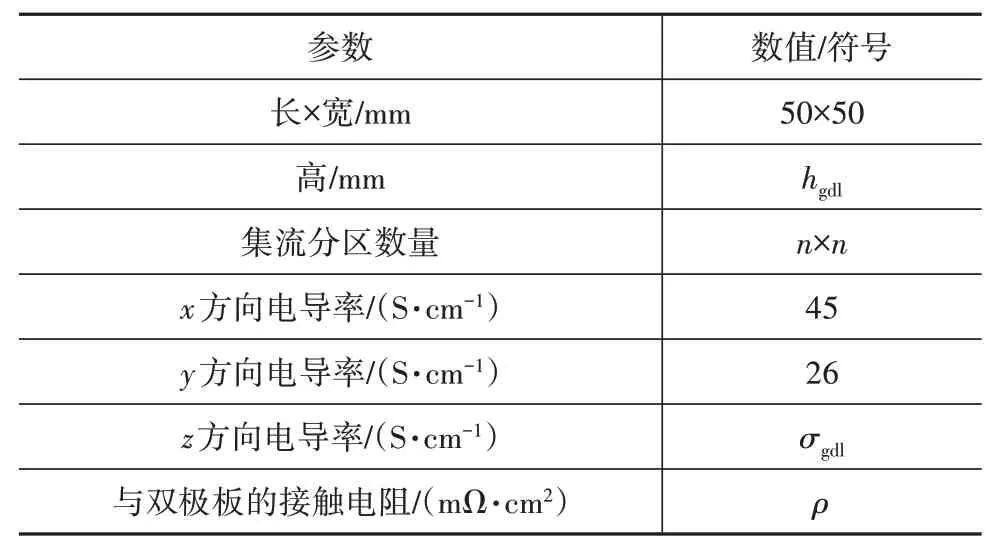
表2 GDL几何模型的参数
2 模型方程和边界条件
本文中研究PEMFC正常工作时的电流密度分布,暂不考虑外部施加交流激励进行电化学阻抗谱测试等情况,认为PEMFC内的电流处于稳态,电场强度不随时间变化,满足拉普拉斯方程:

式中:σ为导体的电导率;φ为电势。
由于GDL和双极板等部件具有各向异性的电导率σx、σy、σz,故写成分量形式:
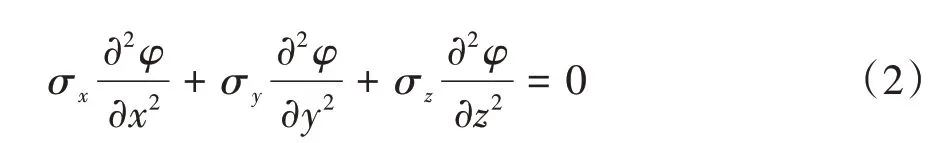
拉普拉斯方程在COMSOL Multiphysics软件的“电流”物理场中以“电流守恒”形式体现。
在本文的仿真求解过程中,设边界为s,可能用到拉普拉斯方程的两种边界条件:

式(3)为狄利克雷边界条件;式(4)为诺伊曼边界条件。对于本文模型:前者表示边界s是等势面,电势为φ0;后者表示边界s处的法向电流密度j0和法向电导率σn已知。
在COMSOL Multiphysics中将已经建立的双极板、GDL和PCB模型形成“联合体”,如图7所示。考虑到仅有PCB电路总电阻以及分区集流焊盘的面积可能对侧向电流有影响,因此将分区电路模型单独进行仿真以得到其直流电阻,再简化为电流方向上具有相等直流电阻的长方体,多个长方体与双极板一侧相接触并形成联合体,如此可在满足仿真需求的前提下,简化网格划分和数值计算。
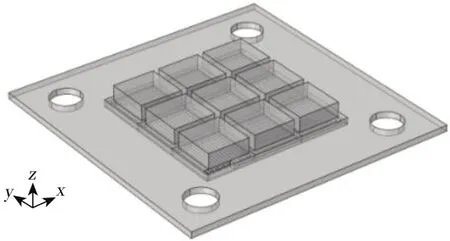
图7 几何模型联合体
在“电流”物理场下进行研究,所有域默认设置为“电流守恒”和0 V电势“初始值”,反应生成的电流以“法向电流密度”的边界条件形式施加于GDL与CL接触的平面上,具体施加区域在后文给出;在各个PCB电路等效长方体上平行于xy平面的自由表面施加“接地”边界条件,因为这些表面均通过集流板连接到同一个外部负载上;忽略镀金焊盘与双极板的接触电阻,而在GDL与双极板的接触面上设置“接触阻抗”边界条件:

式中:n为接触面的单位法向矢量;j为电流密度矢量;ρ为表面接触电阻率,mΩ·cm2;ΔU为两个接触表面的电势差。
3 结果和讨论
对集流分区按照所在的行列数编号,位于第a行第b列的分区编号为ab。为了表征电流产生和收集的相对关系,将分区ab的PCB集流焊盘收集到的电流大小Iab1与该分区电化学反应产生的电流大小Iab0之比定义为分区ab的电流收集率cab,将Iab1与第a′行第b′列分区a′b′的电化学反应产生的电流大小Ia′b′0之比定义为分区ab的电流捕获率tab:
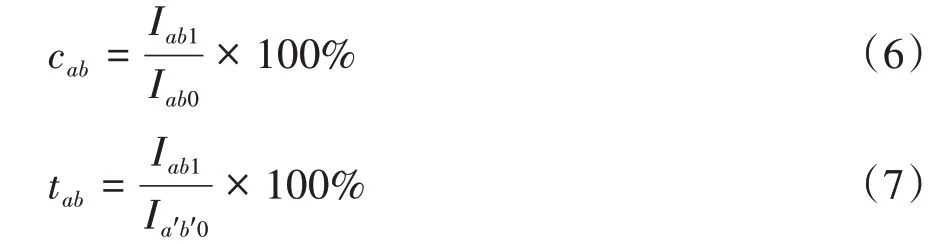
由于实际引起侧向电流的因素为相邻分区之间的电势差,而非绝对电势,因此为了简便,仅在某一个分区的GDL与CL接触平面上施加“法向电流密度”j0,表示该分区与周围分区存在电势差。如此,仅须计算施加了“法向电流密度”的分区的电流收集率和其他分区的电流捕获率。
下面对不同参数进行分组赋值,若无说明,则未确定的模型参数的默认赋值见表3。
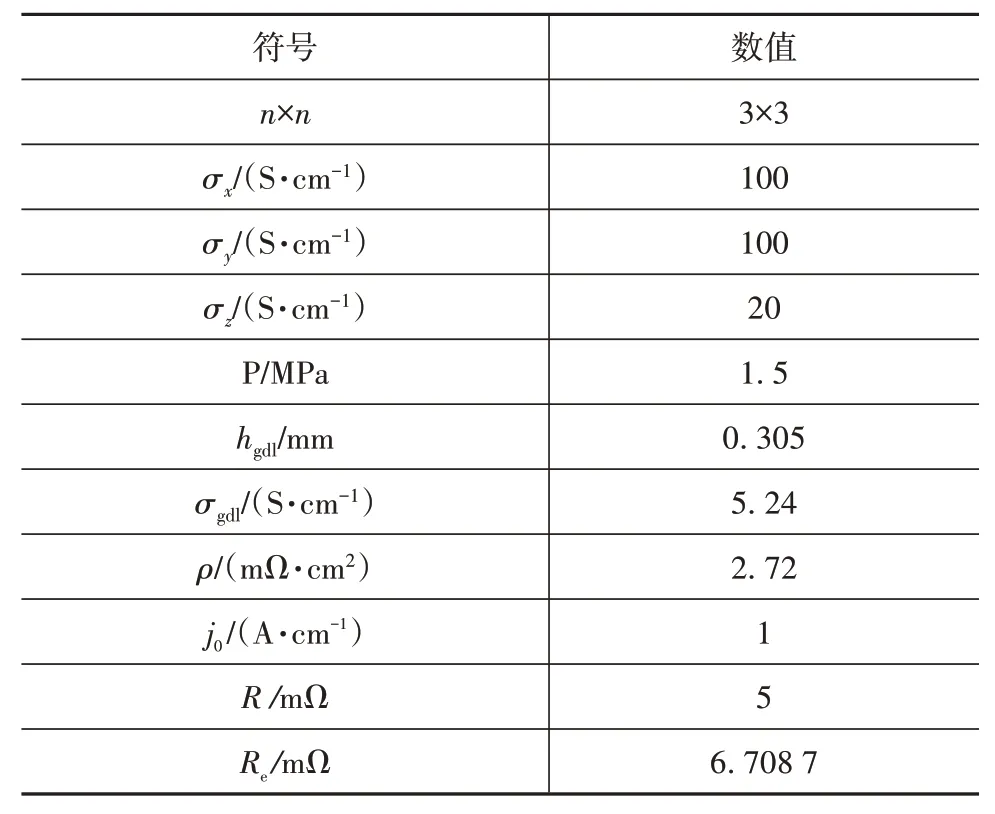
表3 模型参数的默认赋值
3.1 装配压力
参考Mishra等[13]实验获得的GDL⁃10BB在0.5-3.0 MPa内的压缩模量Ec(压强p与压应变ε的比值)的分段函数,单位MPa:
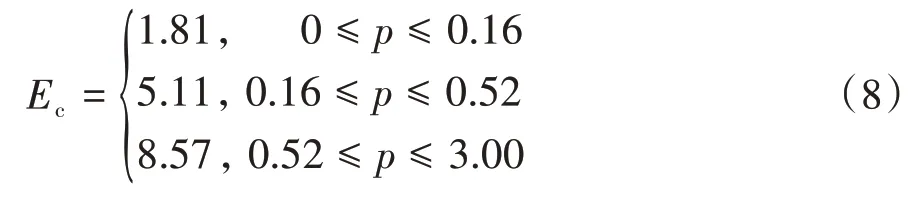
可得压应变与压强的分段函数:

根据GDL⁃10BB的初始厚度0.42 mm即可得到压缩后的厚度hgdl:

Mishra等还给出了GDL⁃10BB的xy平面电阻率Rgdl的计算公式,单位mΩ·cm2:
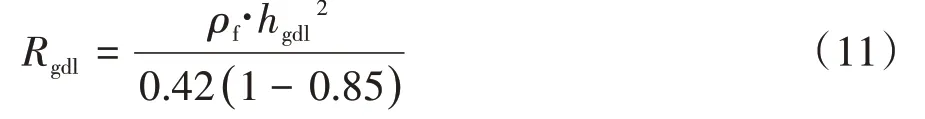
式中0.42与0.85为GDL-10BB的初始厚度(单位:mm)和初始孔隙率,再将初始平面电阻率11.046 mΩ·cm2和初始厚度0.42 mm分别代入Rgdl和hgdl可得系数ρf=3.945,因此GDL模型的z方向电导率σgdl为

Mishra等还测得了GDL⁃10BB与XM9612的接触电阻ρ随压强的变化曲线,Zhou等[14]给出了该曲线的幂函数形式拟合公式,拟合平均误差为4.29%:

选择其中的0.5、1.0、1.5、2.0和3.0 MPa共5个典型压强值计算出相应的GDL电导率、接触电阻率和厚度并分别代入模型,其他参数不变,在分区22施加“法向电流密度”,仿真结果如图8所示,其中具有对称性的分区不重复绘制折线图。
可见,在0.5-3.0 MPa的压强范围内,随压强增大,分区22的电流收集率小幅上升,整个压强区间内上升幅度仅从33.66%上升到35.17%。同时,与分区22有一条邻边的4个分区(邻边分区)电流捕获率均在11%左右,其中分区12的电流捕获率几乎不随压强变化,而分区21的电流捕获率随压强增加有小幅下降;与分区22有一个相邻角的4个分区(邻角分区)均在5%左右且均随压强增加有小幅下降。图8(c)和图8(d)对比了0.5和3.0 MPa下电流收集率和捕获率的分布,可见,压强成倍增长后电流收集率和捕获率的分布差异非常小。PEMFC装配压力对电流测量精度的影响较小的原因可能在于,压强的变化仅使GDL的性质发生了显著改变,而GDL在PEMFC整体厚度上占比较小,其性质变化对于电流分布的影响也较小,所以压强的变化难以显著表现在电流收集率和捕获率上。
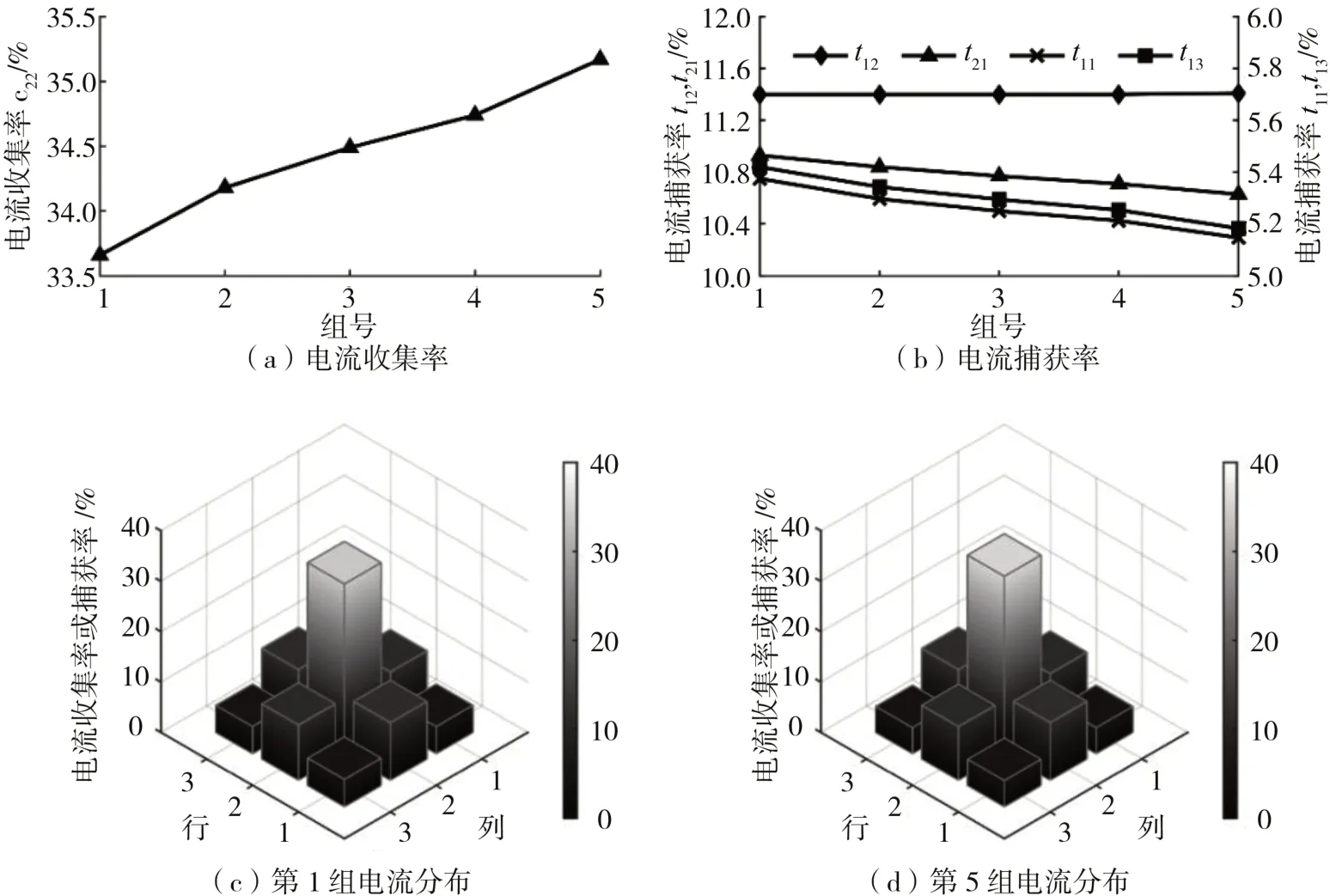
图8 装配压力仿真结果
由于GDL存在一个最佳压缩率以使气体扩散性能和导电性能达到平衡[15],因此在PEMFC中插入PCB时,可按照原有的压紧力进行安装,以保证PEMFC的总体性能,而不必担心影响电流测量精度。
3.2 电阻和分区数量
3.2.1 电阻阻值
选取1、2、5、10、15和100 mΩ共6个常用电阻阻值,求得相应的埋入安装方式下的PCB电路等效阻值,分别为2.708 7、3.708 7、6.708 7、11.708 7、16.708 7和101.708 7 mΩ,将它们代入模型,进行仿真,结果如图9所示。
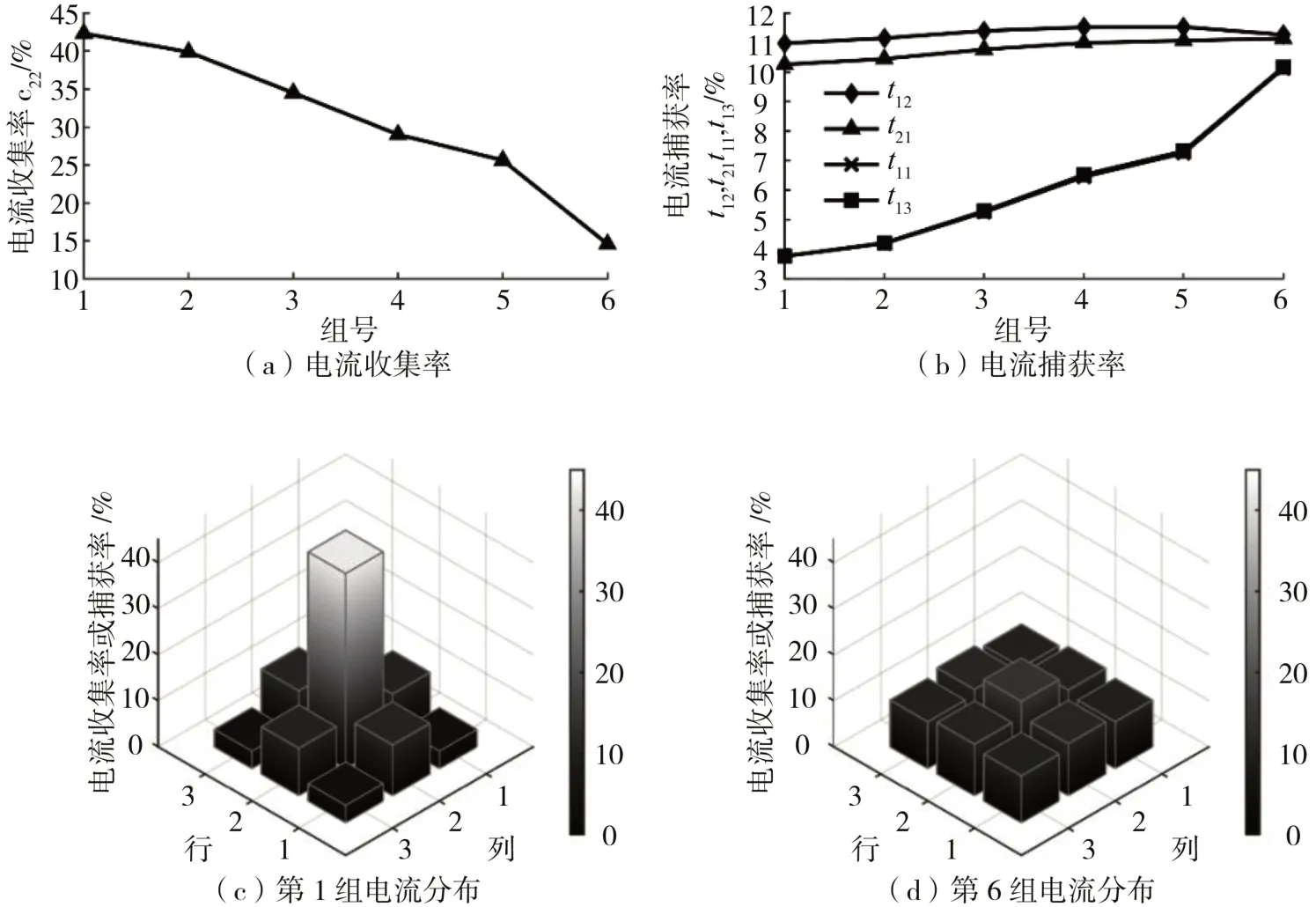
图9 电阻阻值仿真结果
可见,在2.708 7-101.708 7 mΩ的PCB等效阻值范围内,随阻值增大,分区22的电流收集率大幅下降,整个阻值区间内的收集率下降了27.74%,且在阻值较小时下降较快,阻值达到10 mΩ以上后下降速度减慢,这是由于此时已接近100%电流收集率的九等分值11.11%,双极板基本可视为一等势体。图9(c)和图9(d)对比了PCB等效阻值2.708 7和101.708 7 mΩ下的电流收集率和捕获率的分布,表明PCB电路阻值的增长将对电流收集率和捕获率的分布起到明显的均匀化作用。上述电流分布趋势与Eckl等[9]所得的结果类似。相对于装配压力,PCB电路等效阻值对电流测量精度的影响明显更大,可能是因为PCB各个分区电路的等效阻值量级在几个到上百个mΩ级别,大于压强变化时GDL的体电阻和接触电阻的变化量级,因而对电流分布的影响也更加明显。
因此,在PCB上集成分流电阻进行电流检测时,应在保证阻值精度、一致性、温漂和封装尺寸及综合成本和可靠性的前提下,尽量选择较小阻值的电阻元件;若选择较大阻值,则须要对双极板等部件进行分区以抑制侧向电流。
3.2.2 电阻安装方式和分区数量
分区数量改变时,两种电阻安装方式下的PCB电路模型尺寸参数均将发生变化,因此同时研究电阻安装方式和分区数量的影响程度。如前所述,分区数量选择3×3、4×4和5×5 3种常见情况,并选择5 mΩ的电阻阻值和2 mm的双极板厚度,求得表面贴装电阻时PCB电路等效阻值分别为11.375、11.738和11.829 mΩ,埋入安装时则分别为6.708 7、6.192 0和5.767 7 mΩ。上述6个阻值依次按照1-6的组号顺序代入模型,仿真结果如图10所示,施加“法向电流密度”的分区ab对于3×3和4×4为22,对于5×5为33。
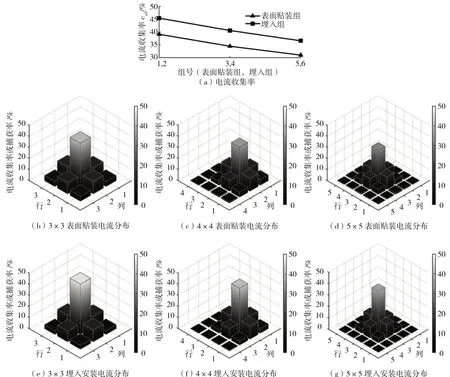
图10 电阻安装方式和分区数量仿真结果
可见,随分区数量从3×3增加到5×5,分区ab的电流收集率存在一定程度的下降,表面贴装组和埋入组的下降幅度接近,分别为8.16%和8.87%,且由于表面贴装组的PCB等效阻值更大,其电流收集率一直低于同等条件下的埋入组,幅度在6%左右。对比不同分区数量和不同电阻安装方式下电流收集率和捕获率的分布则可知,PCB分区数量的增加以及电阻表面贴装方式对于本实验设置下的电流分布有一定的均匀化作用,且电流主要被分区ab的邻边和邻角分区捕获,其他分区的捕获率可忽略。由此可见,电阻安装方式和PCB集流分区数量对测量精度均有一般程度的影响,前者是因为同等条件下表面贴装方式需要更长的中间层导线将带来额外的几个mΩ电阻,而后者的原因则可能在于,分区的面积随数量增加而缩小,因而面积带来的平均效应将趋弱,这将在xy平面内带来更大的等效电势梯度,从而增大侧向电流比例。
因此,须要根据电阻安装方式、MEA有效区域和PCB布线空间进行权衡,选择适中的分区数量;在成本和工艺水平允许的条件下,可选择埋入安装方式以降低电路总电阻,但若难以保证,则埋入安装可能存在可靠性和一致性问题,此时可选择表面贴装方式。
3.3 双极板电导率
有一些研究旨在提高石墨双极板导电性,一般在制造中掺入一些特殊颗粒来实现,根据工艺以及颗粒的种类和比例的不同,石墨双极板的电导率也会不同。参考相关研究,选择(55,20)[16]、(95,50)[16]、(100,20)[9]、(165,103.3)[17]、(180,75)[18]和(230,20)[16]共6组双极板电导率代入模型,括号内数值含义为(x/y方向电导率,z方向电导率),单位S·cm-1。仿真结果如图11所示。
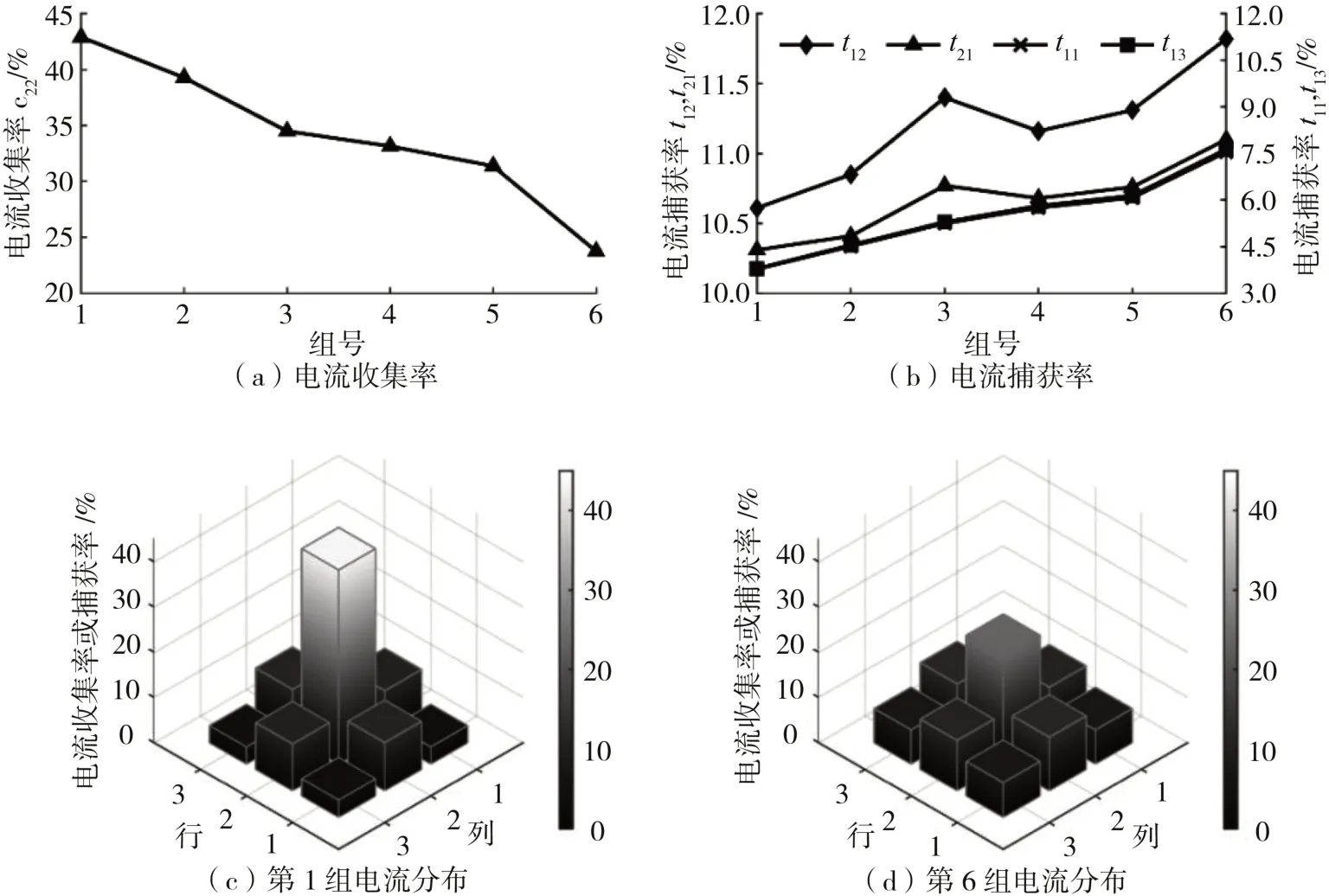
图11 双极板电导率仿真结果
需要指出,分组顺序按照分区22的电流收集率进行降序排列,此排列下双极板的x、y方向电导率呈上升趋势,而z方向电导率则存在大幅波动。第1、3、6组具有相同的z方向电导率(20 S·cm-1),而电流收集率则随x、y方向电导率的上升而下降了19.15%;第2、3组在x、y方向电导率接近的情况下(95 S·cm-1、100 S·cm-1),更低z方向电导率也会带来更低的电流收集率;第1、2组的z方向电导率之比小于x、y方向(0.4<0.58),而第1组则具有更高的电流收集率。上述讨论说明电流收集率主要受x、y方向电导率的影响,侧向电流则正是在xy平面内传导。对比双极板z方向电导率20 S·cm-1时x、y方向电导率分别为55和230 S·cm-1时的电流收集率和捕获率的分布则可知,x、y方向电导率的增加对该分布起到了显著的均匀化作用。
因此,在选择石墨双极板的材料时,不仅要保证z方向电导率足够高以减小双极板在z方向的压降,还应尽量使x、y方向电导率不过高以缓和侧向电流,若已有的双极板不满足上述特点,可考虑更换材料重新定制双极板,或对现有双极板进行分区处理。
3.4 温漂
车载PEMFC实际工作时的温度跨度超过100℃,可能对各部件的电导率产生一定影响。取PEMFC的工作温度范围为25℃±65℃,由于主要供应商的规格书及PEMFC相关研究中一般未提及而忽略GDL和石墨双极板的电导率温漂,故暂假设它们的温度稳定性较差,在给定温度范围内三向电导率温漂均为±10%,约1 538×10-6/℃;5 mΩ电阻元件选择较为常见的30×10-6/℃。上述参数均为负电阻温度系数。第1-3组分别仅计入GDL、双极板和电阻元件的温漂,第4组同时计入三者的温漂,仿真结果如图12所示。
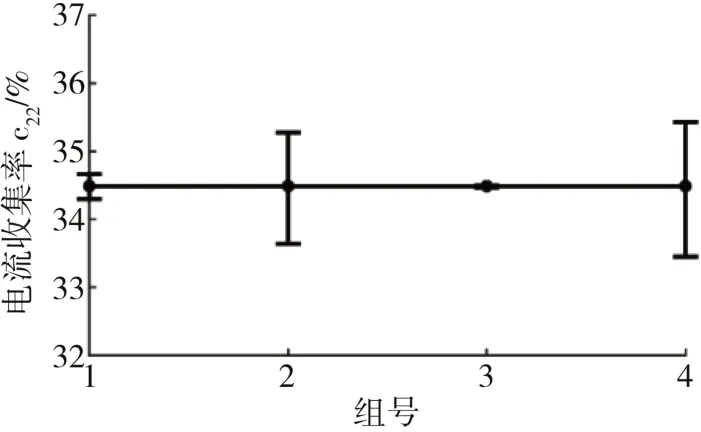
图12 温漂仿真结果
可见,在25℃±65℃的温度范围内,温漂影响最大的双极板也仅使分区22的电流捕获率在33.70%到35.34%的范围内浮动;GDL与电阻元件温漂带来的变化范围分别为34.31%~34.68%和34.48%~34.51%;同时考虑三者温漂时,分区22的电流捕获率也仅浮动在33.55%~35.53%之间,这是在GDL和双极板电导率温漂非常大的假设下得到的,实际温漂可能小得多。由3.3节可知,双极板x、y方向电导率与z方向电导率同步变化时带来的影响会部分抵消,这可能是双极板温漂对电流测量精度影响较小的原因;GDL也存在类似特性,且相对于双极板更小的厚度数量级使得影响更小;成熟的生产工艺则使得电阻元件具有非常好的温度稳定性,故对电流收集率几乎无影响。
因此,温漂对电流测量精度的影响非常小,不影响前文结论,可认为无须针对温漂进行特定的优化设计。
4 结论
本文中参考一种典型的PEMFC结构建立并简化了两种分区电流密度测量PCB方案和相关电池部件的模型,具有较高的实用价值,用于仿真分析分区电流密度测量精度的影响因素,得到的结论对PEMFC单体和电堆的实验和车载应用具有一定的指导意义。
(1)装配压力在0.5-3.0 MPa范围内增加时对测量精度的影响很小,仅使电流收集率上升了1.51%,基本未改变电流收集率/捕获率的分布。
(2)电阻阻值从1 mΩ增加到100 mΩ时显著均匀化了电流收集率/捕获率的分布,使电流收集率下降了27.74%,极大的降低了测量精度。集流分区数量从3×3增加到5×5使得电流收集率在表面贴装和埋入安装时分别下降了8.16%和8.87%,且其他条件相同时两种安装方式的收集率差值在6%左右,说明分区数量和电阻安装方式对测量精度影响有限。
(3)双极板电导率在z方向均为20 S·cm-1,而x、y方向从55 S·cm-1增加到230 S·cm-1时,电流收集率下降了19.15%;在x、y方向电导率均接近100 S·cm-1而z方向从50 S·cm-1减小到20 S·cm-1时,电流收集率下降了4.79%。这说明x、y方向电导率上升对测量精度的负面作用比z方向上升带来的正面作用更为显著。
(4)为了提高分区电流密度测量精度,不必针对温漂进行优化或偏离最佳装配压力,应尽量选择小阻值电阻,根据实际条件和需求权衡电阻安装方式和分区数量,选择电导率在z方向相对较大而在x、y方向相对较小的双极板。

