小学第二学段『题组练习』的设计策略
文|张全苍
“题组练习”就是将练习形式相似、内容联系密切、解法基本相同、思维方法相近的练习串联在一起构成的一组组练习。它具有层次性、对比性、迁移性,对落实基础知识、发展基本技能、增强解题能力、形成知识网络、提升思维能力等都发挥着独特的作用。根据不同的功能可以设计不同的“题组练习”。
一、揭示规律,设计“相似性”题组练习
教学中有很多练习或内容结构相同或解题思路相通,把类似练习组合在一起,引领学生从具体实例中分析概括出同类问题的结构和解题规律。
如学习了“求总路程的相遇问题”后设计的题组练习:
小明和小红同时从两地相向而行,小明每分钟走6O 米,小红每分钟走5O 米,求:
(1)如果4 分钟两人相遇,两地相距多少米?
(2)经过3 分种两人还相距离110 米,两地相距多少米?
(3)经过5 分钟,两人擦肩而过并继续向前走,一转身两人的距离是110 米。两地相距多少米?
这一组题同属于“速度和×时间=路程”的问题范畴,让学生直接去完成第(2)、(3)题有一定难度,思维有障碍,通过这些有层次、有梯度的问题设计,把学生思维引入“最近发展区”,就很容易让学生自行概括出这类问题的结构特征,进而掌握解题规律,达到一题引一组的目的,实现认知水平向更高台阶迈进,让不同层次的学生都能得到不同程度的发展和提高。
二、学会分析,设计“对比性”题组练习
数学知识有很多对立概念,把这些概念建立在对比题组中,让学生在对比题组练习中学会比较,找出题组练习中的异同点,在思辨中逐步形成知识网络体系。
如学习了“用正、反比列解决问题”后设计的题组练习:
(1)学校用地砖铺地,铺3 平方米要地砖27 块,照这样计算,如果要铺地50 平方米,要地砖多少块?
(2)学校用地砖铺地,用每块面积0.08 平方米的地砖,要500 块铺满,如果用每块面积为0.05 平方米的地砖,需要多少块铺满?
在学习用正、反比列解决问题时,“铺地砖”一类的问题是学生错误的高发点,尤其对正、反比例的判定总是阴差阳错。如何帮助学生更好地理解同一情境中的“形似质异”,需要我们把这样的问题让学生进行对比分析,这样会取得事半功倍的效果。在学生独立完成题组练习之后,教师引导学生思考:同样是铺地砖,它们研究的问题相同吗?有什么不同?用比例的知识来解释,分别归属于哪一类?理由是什么?
三、变通求活,设计“变化性”题组练习
练习可以千变万化,力求思维突破“最近发展区”,思维的潜在水平转化为新的现有水平,在新的现有发展基础上,又出现新的思维潜在发展水平,并形成新的“最近发展区”。如此循环,学生在新的思维“最近发展区”中练习,促使学生不断思考,分析问题、解决问题能力逐步得到提高,思维不断向着更高层次发展。只要正确应对各种变化,问题就会迎刃而解。
如学习了“求一个数比另一个数多(或少)百分之几的问题”后设计的题组练习:
(1)甲数是500,乙数比甲数多100,乙数比甲数多百分之几?
(2)甲数是500,乙数是600,乙数比甲数多百分之几?
(3)乙数是600,比甲数多100,乙数比甲数多百分之几?
在理解第(1)题之后,面对第(2)、(3)题的变化,学生在现有发展水平上,出现新的思维潜在发展水平,他们会思考:第(2)题甲数已知,乙数比甲数多几未知;第(3)题乙数比甲数多几已知,甲数未知。这三题的共同点都是用乙数比甲数多的数去除以甲数,新的思维点被找准并解决。通过变化“解一题会一类”,提高了应变能力,发展了思维品质,达到举一反三、触类旁通之目的。
四、织结网络,设计“拓展性”题组练习
如果一个数学问题能从不同角度去延伸、去拓展,既能激发学生思维,把握知识的内涵和外延,又能加深学生对知识的理解,学生思维的创造性、变通性、深刻性得以提高,真正形成知识系统化、网络化,达到解决一个问题、学会解决一类问题的目的。
如学习了“同分母分数加减法”后设计的题组练习:
(1)
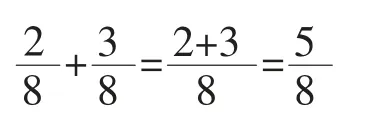
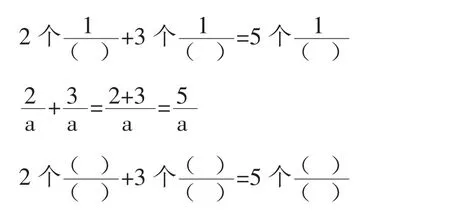
(2)
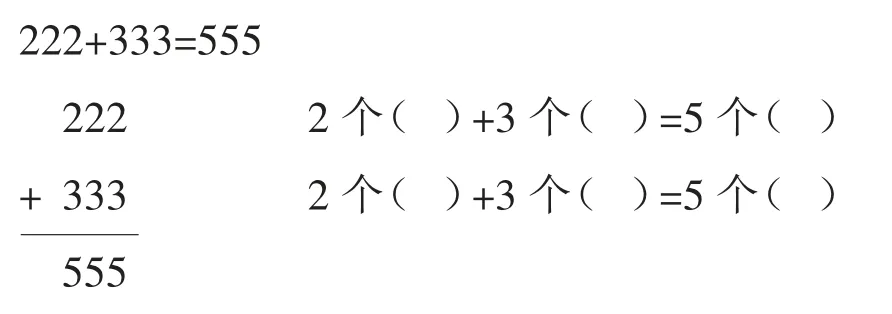
(3)

思考:你发现了什么?
在组织学生学习了“同分母分数加减法”一课后,从加法意义和本源入手,安排了这样的练习,学生明白整数、小数加减法计算相同数位要对齐,分数加减法计算必须分数单位相同才能直接相加减,其实质是“单位相同”才能相加减。这个练习把分数和整数、小数加减法联系起来,帮助学生梳理和沟通了同分母分数加减法的法则和算理。当数学计算神秘的面纱层层被掀开的同时,学生才恍然大悟,原来我们学习的整数、小数、分数的加减法计算,其实计算的道理是一样的。这样的练习设计,能激活学生原有的认知基础,寻找知识的本质,让知识产生深度的串联和广泛迁移,使知识网络化、系统化。
我们在使用“题组练习”时一定要仔细分析每个题组练习的内涵,把握题组练习的目的,做到“题”尽其用,让题组练习增值:通过题组练习,展示知识的发生过程,加强对数学知识实质的理解,沟通知识间的联系,促使知识系统化、网络化,挖掘学生的最大潜能,促进学生思维能力的发展,让不同层次的学生都能得到发展和提高。

